Application of topography fast marching method in landslide

YANG Junjie, SUN Hui, 2*, WEI Chengwu, JIANG Zhenghong and LI Meng

1. Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, Chengdu 611756, China;2. School of Resources and Environment, University of Electronic Science and Technology of China, Chengdu 611731, China;3. China Railway Academy Chengdu Company, Limited, Chengdu 610036, China

Abstract: Geophysical exploration methods are important tools for landslide disaster assessment, landslide treatment scheme design, and landslide prevention engineering. Seismic exploration, as an important geophysical exploration method, plays an critical role in geological disaster evaluation. Traveltime is one of the most frequently used seismic attributes. Among many different traveltime calculation methods, the fast marching method (FMM) is featured for its advantages in high efficiency, high accuracy and strong stability. In this paper, the velocity models are established according to the real landslide models, and then the topography FMM is applied to these landslide models. The calculation results show that topography FMM outperforms in calculating the traveltime for landslides.

Keywords: fast marching method; seismic exploration; traveltime calculation; landslide; topography

0 Introduction

As one of the serious natural geological disasters (Zhang & Zhang, 2000), landslides are very destructive and have high frequency of occurrence. It is of great significance to monitor, explore and prevent landslides (Yin, 1998; Zhang, 2000). Many geophysical exploration methods have been successfully used in the exploration of landslide. Peng and Chen (1996) applied shallow seismic method to landslide disaster investigation, and achieved good results. Xieetal.(2004) introduced shallow seismic exploration method and high-density electrical method to investigate landslide, the exploration results are basically consistent with the later drilling geological data, which shows the feasibility and accuracy of applying these two methods to the landslide investigation. Yuanetal.(2010) applied the integrated geophysical prospecting technology to the investigation of large accumulation landslides. After mutual verification of va-rious geophysical prospecting results, a more accurate geological interpretation was obtained, which shows that the integrated geophysical prospecting technology has a good effect on the engineering geological investigation of accumulation landslide. Geetal.(2014) applied a seismic refraction method and a high-density electrical method in ancient landslide exploration, determined the sliding surface, landslide nature and thickness of landslide mass, which played a positive role in landslide exploration. Heetal.(2015) confirmed that the comprehensive geophysical method can effectively reduce the ambiguity of geophysical exploration and improve the interpretation accuracy of the results, showing the important role of the integrated geophysical method in the exploration of landslide and other geological disasters. Heetal.(2016) applied the high-density electrical method to the investigation of landslide geological disasters. This method can directly and concretely reflect the shape, scale and structure of landslides, and lay a stable foundation for the disaster prevention.

Among the landslide exploration methods, seismic exploration methods are of great significance for landslide exploration (Zhuetal., 1995). Traveltime is an important research attribute of seismic exploration, which has an important impact on the application effect of seismic exploration. There are many traveltime calculation methods (Vidale, 1988; Asakawa & Kawanaka, 1993; Qin & Chen, 2000; Lietal., 2004; Zhangetal., 2006; Hanetal., 2008), among which FMM has the advantages of high accuracy, high efficiency and unconditional stability. FMM was proposed by Sethian (1996) to study curved surface problems in complex media. Sethian and Popvici (1999) introduced FMM into geophysical fields and applied it to calculate the traveltime. Zhu (2001) applied FMM to 3D Kirchhoff prestack migration, 3D Kirchhoff post stack migration and 3D Kirchhoff forward modeling, and calculated the traveltime of the complex geological models. Rawlinson and Sambridge (2004a, 2004b) used FMM method to track the ray path of reflection wave, converted wave and multiple wave, and calculated the traveltime of seismic wave. Sunetal.(2007, 2009, 2010) introduced FMM into the traveltime calculation of seismic wave under the condition of complex topography in the following aspects: In 2007, a traveltime calculation method of seismic wave under complex surface conditions was proposed, and its feasibility was proved; in 2009, a new traveltime calculation method based on linear interpolation and narrow-band technology was proposed, which proved that the method can effectively handle complex topography, and has good adaptability and stability; in 2010, on the basis of the original FMM, the traveltime calculation under complex topography was improved by introducting different difference scheme and the addition of new grid node types. Through the application of the improved method, it is found that the algorithm has high accuracy, high efficiency and strong stability. Sunetal.(2012) introduced FMM into the traveltime calculation of 3D complex topography model. Wangetal.(2016) introduced the complete ternary tree heap sorting to the FMM seismic wave traveltime calculation based on the original heap sorting of FMM, which is more efficient than the binary tree.

Based on previous studies, this paper first establishes velocity models based on several typical large-scale landslides (Wuetal., 2010; Xu & Dong, 2011; Huang & Zhao, 2010; Zhongetal., 2020), and then topography FMM is employed to calculate the traveltime of these models. The numerical tests show that the topography FMM performs well in the traveltime calculation of landslides. The principle of topography FMM is addressed as follows.

1 Basic principles

FMM obtains traveltime by solving the Eikonal equation, which is

│▽t│v=1

(1)

Wheretis the traveltime;vis the velocity of the model. ▽ is the notation for the gradient.

The upwind differential scheme is used to solve the equation, the format is as follows:

=Si, j

(2)

(3)

(4)

(5)

(6)

Equation (2) can be simplified as:

(7)

In this paper, an improved first order difference operator is used, the formula of local difference algorithm is as follows:

(8)

(9)

t(i,j)=t(i±1,j)+Si, jhort(i,j)

=t(i,j±1)+Si , jh

(10)

2 Realization of topography FMM

FMM is based on the upwind difference scheme to solve the local Eikonal equation. In the implementation, the narrow-band expansion technique is introduced to approximate the wavefront. Then the binary tree heap sorting is used to select the minimum traveltime point in the narrow-band as the expansion evolution node, and the grid node that has completed the calculation is determined by setting the attribute of the grid node. Finally, the extended evolution of wavefront is simulated approximately by updating the grid nodes in the narrow band. The implementation process of topography FMM is shown in Fig.1.

As shown in Fig 1, the attributes of all grid nodes are as follows: narrow-band nodes, accepted nodes, far away nodes, and surface node. Among them, the accepted node is the node that has completed the traveltime calculation, the narrow-band node is the node that is calculating the traveltime (the node within the narrow band), the far away node is the point that has not calculated the traveltime (different from the surface point), and the surface node refers to the point above the surface.

Fig.1 Wavefront expansion of topography FMM

In the implementation of topography FMM, one of the core technologies is heap sorting technology. The implementation process of heap sorting technology is described in detail as follows: Heap is a sequential structure of complete binary tree. The operation of heap sorting technology is divided into initialization heap and reselection heap:T(n)=2nlog2n+o(n),nis the size of the array. The first step is to initialize the heap data, which is accompanied by the initialization in the narrow band. The traveltime values of the grid points adjacent to the source point are saved according to the structure of the heap data, and the mini-mum traveltime value is placed at the top of the heap; The next step is to update the top element of the heap, which corresponds to the selection of the minimum traveltime node, and reconstruct the heap structure while updating the elements; The final step is to insert a new element or update the traveltime value of the original element, and rebuild the heap structure according to the size of the traveltime value. The process of heap sorting is shown in Fig. 2.

Fig.2 Heap sort application process

The calculation steps of seismic traveltime of all grid nodes in the computational domain are divided into two steps: initialization and narrow band expansion. Initialization is to select the source point of the grid node as the initial point, and then use the corres-ponding formula to calculate the traveltime of eight grid points near the initial point, and take these eight points as the initial points. Narrow band expansion refers to selecting the smallest traveltime point in the narrow band as the next acceptance point according to the traveltime calculation results, determining the attributes of the four points adjacent to the point, and finally judging whether the narrow band is empty. If there are no points, the circulation will be end. Otherwise the circulation will continue. The specific flow chart of traveltime calculation of seismic wave is Fig. 3.

3 Calculation and analysis of model

In order to apply topography FMM to landslide exploration, we select four typical large-scale landslides and establish seismic velocity models as shown in Fig 4. Fig. 4a is a model based on the velocity of different layers of Wenjiagou landslide, the velocities from low to high are 2 000 m/s, 2 500 m/s, 3 000 m/s, 4 000 m/s and 4 500 m/s, respectively, the model size is 701×2301, the spacing is 2 m, and the source location is (290 m, 805 m). Fig. 4b is a model based on the velocity of different layers of Xiao-jiaqiao landslide, the velocities from low to high are 2 000 m/s, 3 000 m/s, 3 500 m/s, 4 000 m/s and 5 000 m/s, respectively, the model size is 521×805, the spacing is 0.5 m, and the source point location is (200 m, 380 m). Fig.4c is a model based on the velocity of different layers of Donghekou landslide in Qingchuan County, the velocities from low to high are 1 500 m/s, 2 000 m/s, 2 400 m/s, 2 500 m/s, 3 500 m/s, 4 000 m/s, 4 500 m/s and 5 000 m/s, respectively, the model size is 701×1301, the spacing is 2 m, and the source point location is (400 m, 352 m). Fig.4d is a model calculated based on the velocity of different layers of Diexi giant paleo-landslide, the velocity from low to high are 3 000 m/s, 3 500 m/s、 4 000 m/s, 4 800 m/s and 5 000 m/s, respectively, the model size is 801×2001, the spacing is 2 m, and the source point location is (320 m, 758 m).

Fig.3 Flow chart of topography traveltime calculation

Fig.5 shows the traveltime calculation results for the four landslides in Fig.4. Fig.5a is the traveltime

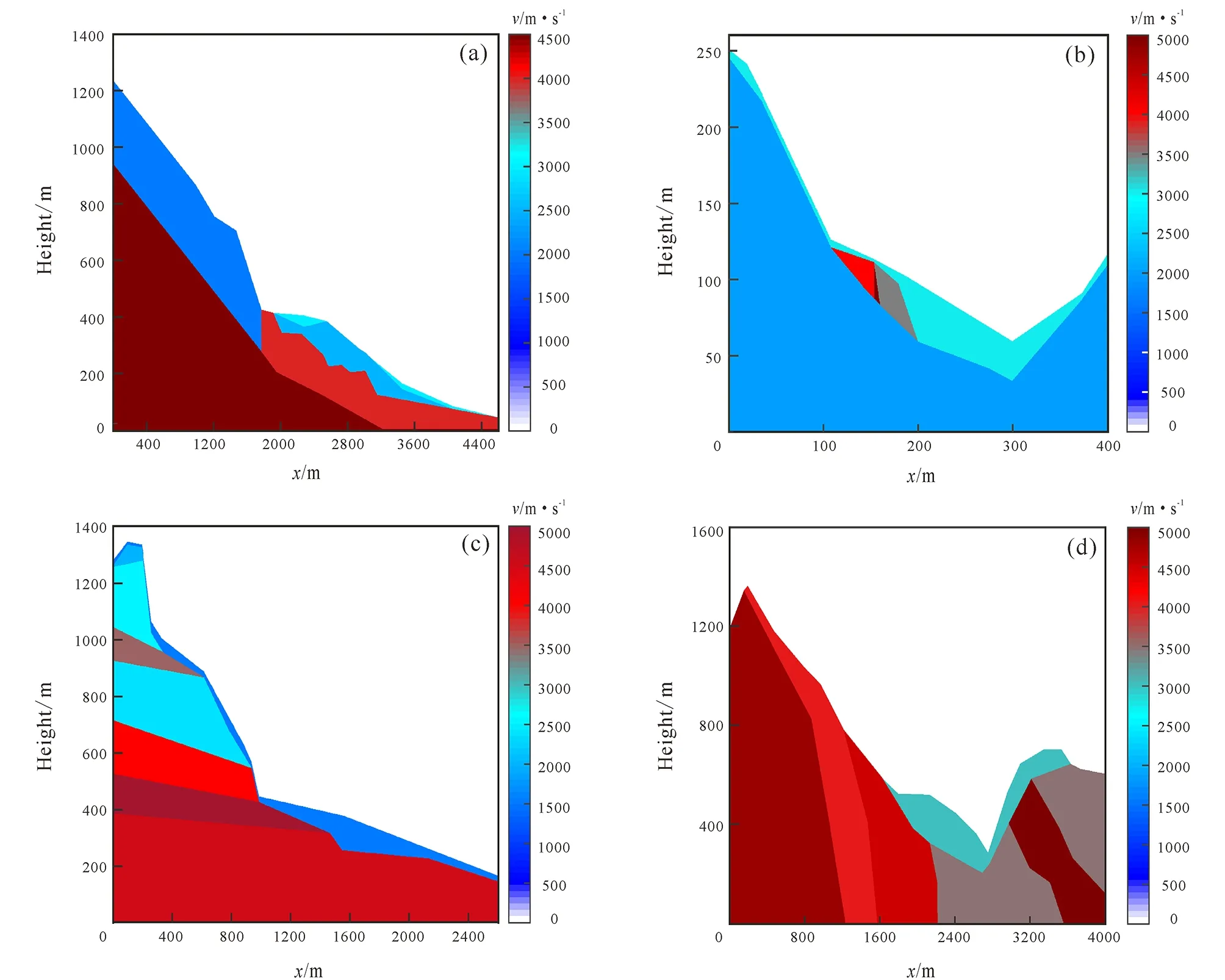
Fig.4 Traveltime velocity model of seismic wave with topography FMM

isochron of seismic wave of Wenjiagou landslide, Fig.5b is the traveltime isochron of seismic wave of Xiaojiaqiao landslide, Fig.5c corresponds to the traveltime isochron of seismic wave of Donghekou landslide in Qingchuan County, and Fig.5d corresponds to the traveltime isochron of seismic wave of Diexi giant paleo-landslide. The isochron distribution in the figures conforms to the law of seismic wave propagation, which confirms the effectiveness and practicability of the topography FMM in the traveltime calculation of landslide.

Fig.5 Traveltime isochron chart of seismic wave based on velocity model

4 Conclusions

This paper focuses on how to apply the topography FMM to traveltime calculation in landslides. The paper first introduces the principle and implementation strategy of the topography FMM, then establishes seismic velocity models for four typical landslides, and finally uses topography FMM to calculate the traveltime of these landslide models. The traveltime isochrons obtained by FMM calculation conform to the law of seismic wave propagation, which proves that the complex topography FMM can be effectively applied to the traveltime calculation for landslide geological bodies. The topography FMM has important application prospects in the seismic exploration methods for landslides.