试值代入法计算盐水溶液的pH值

郝绍鹏

(金堆城钼业股份有限公司化学分公司，陕西渭南，714000)

在教学、科研和化工生产中经常需要计算盐水溶液的pH值，在已知各平衡常数和溶质浓度计算pH值时，通常采用消元整理后解关于[H+]一元高次方程。由于目前没有精确表达高次方程根的方法，计算方法主要分为两大类：一类是在解方程前先进行近似处理，然后由简化的近似求解公式求解的粗略计算[1，2]；另一类是依托高次方程使用二分法、迭代法等并借助计算机进行精确计算[3，4]。近似公式求解采用了近似处理前置的处理方式，在缺乏大量实验数据印证的情形下，无法评估其计算结果的偏差。二分法、迭代法进行精确计算时，将化学问题高度抽象成数学运算，不易感知计算过程与化学原理之间的联系，同时采用此类方法需要较高的数学逻辑认知或专业软件辅助，在实际应用中也不易实施。

若将[H+]也看作是已知值，代入所有过程等式，则各等式应全部成立。此时的计算过程是一组数字简单、大量的混合运算以及数量比较，不再涉及复杂的高次方程解法。

1 计算原理

1.1 主要运算式

设有正盐或酸式盐MzZm的水溶液体系，碱离子Mm+进行n级水解，强碱盐n=0，弱碱盐n=m；阴离子Zz-全部以Xx-、Yy-及其水解产物的形式存在，Yy-发生y级水解；Xx-发生a级水解，同多酸根体系a=x，体系无同多酸根a=0；Xx-、Yy-、Zz-中特征元素原子个数分别为s、t、r(如碳酸根、碳酸氢根中的碳元素)。建立其物料平衡式(MBE)和电荷平衡式(CBE)，并将两式中的各平衡浓度用[Xx-]、[Yy-]、[H+]表示，整理出方程组及其解的表达式；建立[Xx-]、[Yy-]之间关系式的通式(以下简称试算式)。如图1。

图1 主要算式及说明

对于给定的盐，各参数和试算式确定。各平衡常数和溶质浓度已知时，每试选一个[H+]的猜测值，可算出方程组的解，代入试算式中可算出k的一个试算值(为了避免混淆，称平衡常数k的实际值为目标常数，试值代入计算所得的k值称为试算值)。与目标常数最接近的试算值所对应的[H+]猜测值，即为所要计算的氢离子平衡浓度，进而算得pH值。

1.2 试值选择

分组选取pH值实现对[H+]的试值选择。选取p组pH值，各组内pH值为等差数列，各组的公差依次减小且成等比数列，公比为1/q。第二组及其后各组均有2q-1个pH值，最后一组的公差小于所需精度，第一组结合第二组使全部选值可覆盖pH值1至14。从第一组开始依次代入计算，选取最接近目标常数的试算值对应的pH值，作为后一组pH值的中位数。

第一组在理论pH值附近捕获一个节点，其后各组在捕获的节点附近提高计算精度并逼近理论值。上述选值中的重复取值，是为了便于文字描述和电子表格编辑，实际应用中可合理避免。

2 计算的实现

使用EXCEL电子表格作为工具，对水解不高于7级、pH值1至14范围内的体系进行计算，计算流程、中间辅助计算值、主要函数公式见图2。图中指数差指试算值常用对数与目标常数常用对数的差的绝对值；获得计算结果与获取中位数所用函数相同，改变其计算单元格范围即可。

图2 软件计算流程示意图

3 计算示例

示例中第一组9个pH值，中位数为7，公差1.458；各组公差之间的比例为3，共8组；pH值精度±0.000667。

3.1 同多酸盐计算示例

鉴于同多酸盐在水溶液中的平衡状态比较复杂，这里将(NH4)6Mo7O24水溶液体系视为仅有两种同多酸根，以此为模型介绍同多酸盐水溶液pH值的计算，参数设置和水解见表1[5，6]。对1mol/l、0.1mol/l、0.01mol/l、0.001mol/l、0.0001mol/l(NH4)6Mo7O24水溶液pH值的计算结果分别约为5.855、5.461、5.045、4.614、4.26。

表1 同多酸盐水解

3.2 正盐、酸式盐计算示例

分别以Na3PO4、Na2HPO4、NaH2PO4水溶液pH值的计算为例，参数设置和水解见表2[6]，计算结果见表3[1]。

表2 正盐、酸式盐水解

计算多元弱酸正盐和酸式盐水溶液的pH值，不仅可以获得相对精确的结果，而且从计算过程可以观察到一些现象。如表2中三种盐的参数设置只有z(阴离子价态)不同，结合表3数据可知，浓度相同时，参数z的变化引起计算结果的变化。再如表3中，比较指数差可以发现，在相同精度内，NaH2PO4的指数差明显较大；通过增加计算行提高计算精度，pH值精度达到约±3.76×10-9时，指数差分别为0.03(1mol/l)、0.06(0.01mol/l)、0.003(0.0001mol/l)。

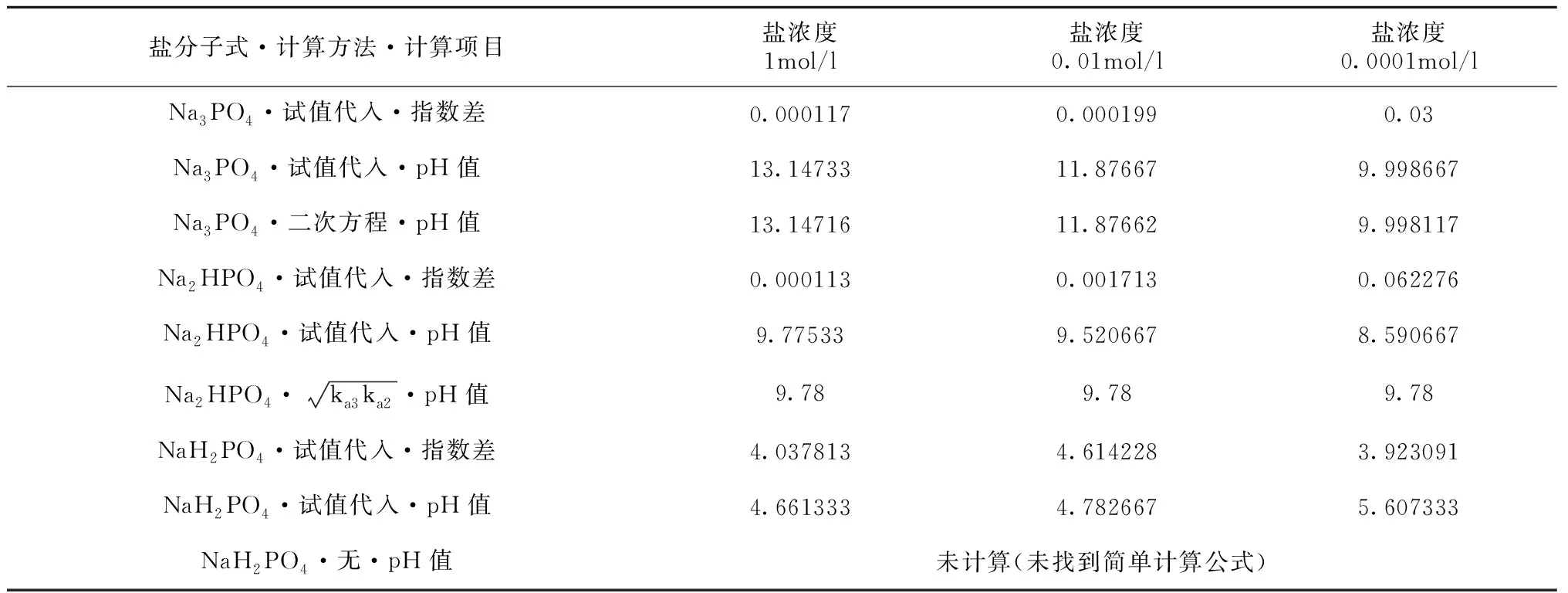
表3 正盐、酸式盐水溶液pH值计算对比

4 总结与结论

试值代入法为计算pH值提供了一种新的思路，将推导高次方程求根公式的难点转化为大量简单计算，再利用电子表格实现求值，获得了良好的效果。

此方法计算范围广泛，可以完整地实现对正盐、酸式盐水溶液pH值的计算，可以尝试对同多酸盐水溶液pH值的计算。虽然在电子表格中的编辑和设置比较复杂，需要足够的耐心和细致；但此方法的过程原理简单，且可用日常办公软件实施，不需要高深的理论知识和专业软件即可实现对pH值的高精度计算，仍然适用于广大教学和技术研究人员使用。

除计算结果在所需精度内做近似处理外，计算过程中不做其他近似，完整考虑了水的离解和酸碱的各级水解，使计算结果获得较高的精度。且从过程中可观察到一些现象，如阴离子价态对pH值计算结果有影响；观察指数差用以评估偏差等。