界面弹性模量对混凝土梁影响的三维动态研究*

2021-09-10张亚芳章凯刘浩甘伟

中山大学学报(自然科学版)(中英文) 2021年4期

张亚芳，章凯，刘浩，2，甘伟

1. 广州大学土木工程学院，广东广州 510006

2. 深圳市市政设计研究院有限公司，广东深圳 518029

混凝土梁是工程中使用最广泛的构件之一，在梁构件内部混凝土和筋材之间的界面是结构应力的过渡区域，是决定能否实现筋材与混凝土基体共同工作的关键因素，因此研究界面性质对梁破坏过程的影响具有重要意义。

20 世纪开始，国内外有关学者开始研究界面对材料性能的影响［1-6］，取得了许多成绩。一些学者利用各种物理实验方法研究了纤维的某些性能，例如利用拉拔实验［7-10］去研究纤维的拉拔特性及界面剪切强度。然而，由于界面存在于材料的内部、性质特殊并且尺寸微小，因此在全面揭示界面性质对材料开裂破坏机理影响的研究方面，物理实验方法存在一定的局限性。随着计算机的迅速发展，近年来许多学者开始采用有限元仿真方法研究界面强度［11-14］和界面弹性模量等力学性质对材料性能的影响。在界面弹性模量影响材料性能的研究中，杜敏等［15］利用基于单位分解法及水平集理论的新型数值模拟方法模拟裂纹在材料体内的扩展过程，研究了单轴拉伸数值实验下混凝土的界面弹性模量对混凝土力学性能和破坏模式的影响；Lee 等［16］提出了一种三相模型和材料不连续有限元相结合的混凝土数值模型，对具有复杂界面的混凝土进行了三维分析。

但总体来说，探索界面弹性模量对材料性能影响的研究相对极少，并且目前现有的文献也多是建立在材料均匀假设和静态条件下开展的研究。众所周知，实际的混凝土材料是非均匀分布的，且大量的混凝土梁是在动载工况下工作的。针对这种现状，本文在考虑钢筋混凝土梁各相材料细观非均匀分布的前提下，利用RFPA3D-Dynamic程序模拟了三点弯曲梁在三维动载情形下的物理力学性能，实现了试件从裂纹萌生、扩展直至失稳破坏的全过程模拟，开展了界面弹性模量变化对钢筋混凝土梁相关性能影响的分析。

1 数值模拟模型

混凝土是一种典型的非均匀材料，本研究利用RFPA3D-Dynamic 分析软件［17］，采用Weibull 双函数曲线对试件单元的强度、泊松比、弹性模量和密度等进行随机非均匀性赋值，其曲线函数为

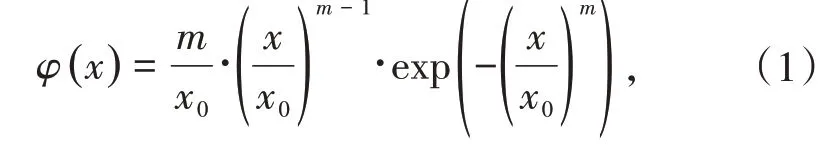
其中x为单元的某一力学参数；x0表示该参数对应的平均值；m 为均质度系数，m越大时，材料越均匀。

细观单元的损伤主要是拉伸和剪切破坏造成的，本文采用拉伸截断的摩尔库伦准则作为损伤判断依据［18］。当单元满足最大拉应力准则时，认为该单元发生拉伸损伤，如式（2）所示。

其中σ1为最大主应力，σt为单向应力状态下的极限应力。

当细观单元的应力状态满足摩尔库伦准则时，则该单元发生剪切损伤，如式（3）所示。其中，最大拉应力准则具有优先权。

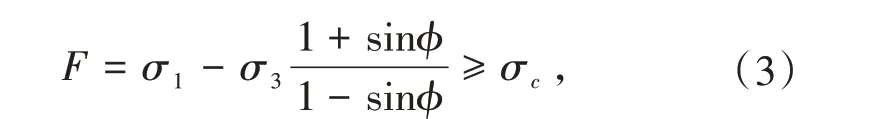
式中ϕ为内摩擦角，σc为单轴抗压强度；σ1和σ3分别为最大和最小主应力。

按照勒梅特（Lemaitre）应变等价原理，可以建立损伤变量和应变之间的关系，本构关系中的损伤变量可以描述为

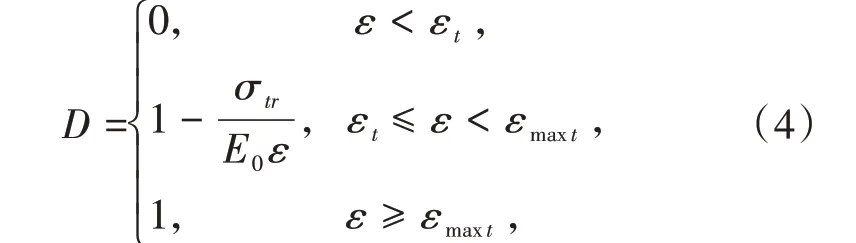
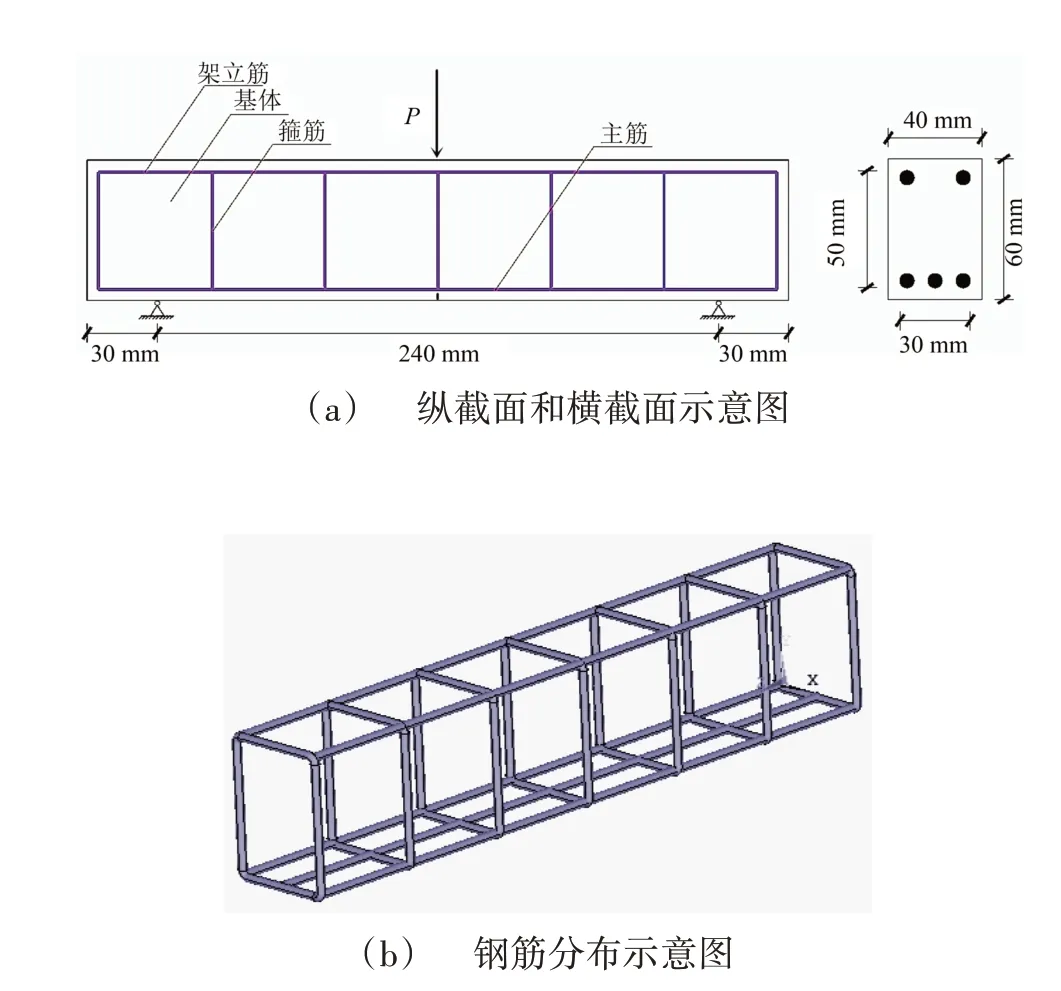
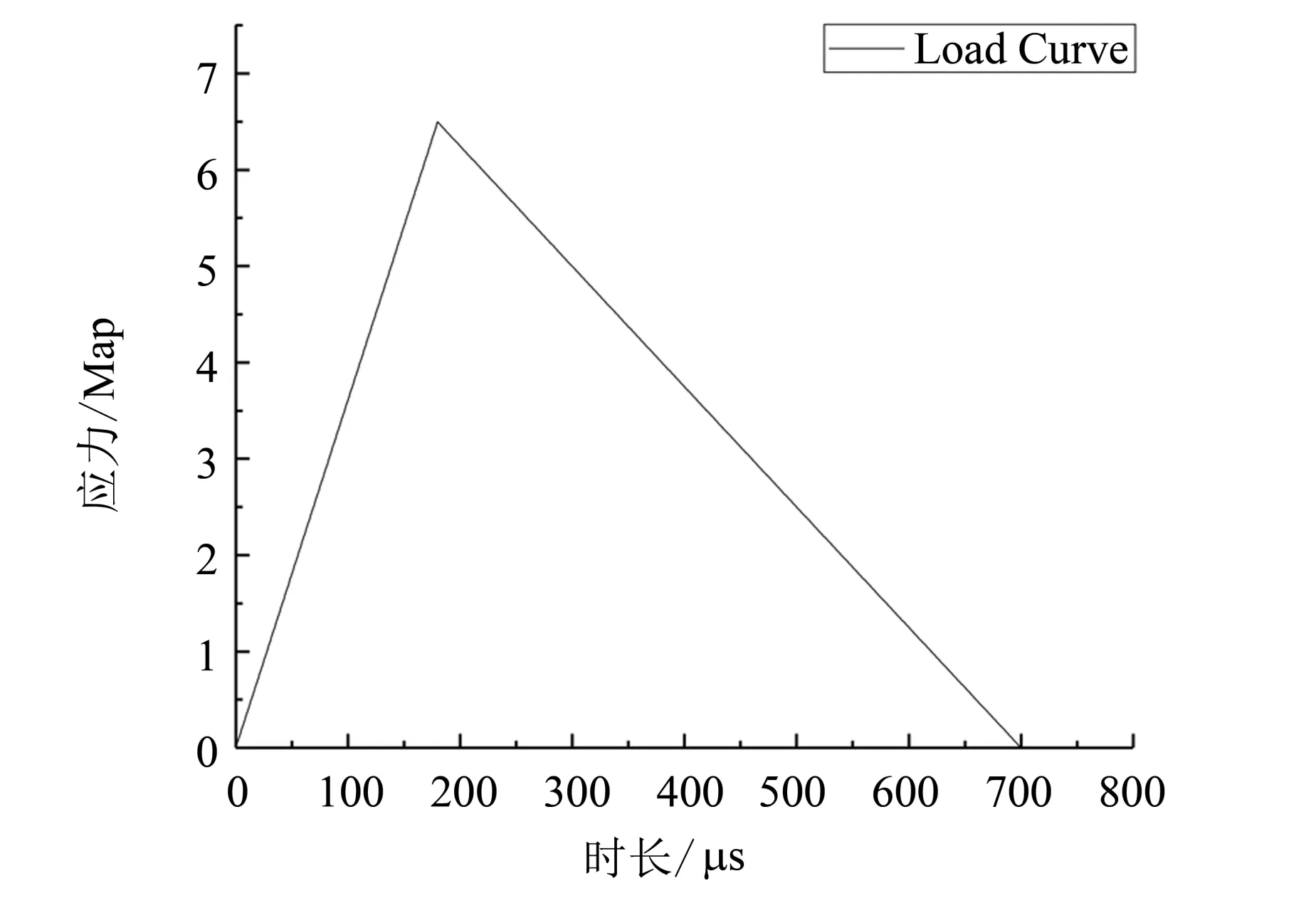
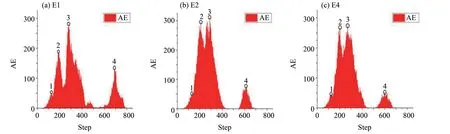
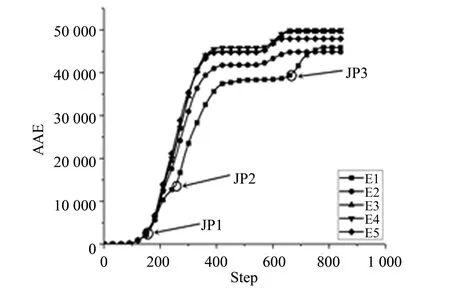
其中σtr是材料单元的残余强度，E0是材料的初始弹性模量，εt是弹性极限所对应的拉伸损伤应变阈值，εmaxt是材料单元的极限拉伸应变。D为损伤变量，当材料处于完全损伤状态时，D= 1；当材料处于完全没有损伤的状态时，D= 0；当材料处于不同程度的损伤状态时，0

图1为钢筋混凝土梁的数值模型示意图，其尺寸为60 mm×40 mm×300 mm，是在梁下部的正中间位置设置预留缝的简支梁，预留缝宽度为2 mm，高3 mm，长40 mm，梁的保护层厚度为5 mm。模型的纵向钢筋包括上部两个架立筋和下部三根主筋。假设下部的三根主筋包裹着界面，界面厚度为1 mm。本文研究了界面弹性模量分别为0.1、1.0、3.5、5.5、7.5 GPa 的五个模型。为方便描述，将其分别表示为E1、E2、E3、E4、E5，其中E1为低界面弹性模量试件，E2和E3为中界面弹性模量试件，E4 和E5 为高界面弹性模量试件。表1为试件各相材料力学参数及均质度值。

表1 数值模型力学参数1）Table 1 Mechanical parameters of numerical model

图1 钢筋混凝土梁数值模拟模型Fig.1 Numerical simulation model of reinforced concrete beams

加载采用三角形压缩应力波，加载曲线如图2所示，总加载时长700 μs，每步1 μs，总共700步，应力幅值6.5 MPa，应力波抬升时间180 μs。1）括号内数值代表材料的均质度，基体的拉压比为1/10，钢筋的拉压比为1；界面的弹性模量对应试件E1～E5的弹性模量值。

图2 动态加载曲线Fig.2 Dynamic loading curve

2 计算结果分析

随着界面弹性模量的变化，钢筋混凝土梁在三点弯曲作用下的破坏模式发生显著变化。篇幅所限，本文仅对E1、E2、E4 三个梁试件的破坏过程进行描述。

在加载前期，由于预留缝处的拉应力集中，E1、E2、E4 的破坏均是从此处开始。随着加载的继续，预留缝萌发的裂纹到达主筋的界面处，同时由于材料的非均匀性，基体中出现了许多随机破坏的单元。

试件E1 的裂纹尖端遇到钢筋后发生偏折，钢筋的上下界面开始脱粘。随后，由于梁下部拉应力的作用，箍筋与主筋连接处开始萌生出微裂纹，预留缝处的裂纹以垂直主筋的顺筋方向向上进一步扩展，如图3（a）的Step-242 所示。当加载到274 步时，箍筋与主筋连接处萌生出的微裂纹由于拉应力的作用发展为沿箍筋的宏观裂纹。由于E1的界面较柔，破坏状态图上以弯曲拉应力引起的弯曲裂纹和顺筋裂纹占主导地位，如图3（a）的Step-274所示。随后在箍筋与主筋的连接处，由于应力集中的作用，沿着箍筋开始萌生裂纹并向上扩展。当扩展至梁高的约1/2 处时，在剪应力的作用下以大致45°角的方向继续向上扩展至上部架立筋处。然后，由于钢筋阻止了裂纹继续向上扩展，裂纹便沿着架立筋与混凝土的界面扩展，直至左右两条裂纹在梁上部的中间汇合，最终在混凝土中形成了沿箍筋和架立筋扩展的宏观“拱”形裂纹，如图3（a）的Step-420 所示。最后梁上部和内部混凝土逐渐被压碎，如图3（a）的Step-670所示。钢筋混凝土梁的上部混凝土被压碎，标志着梁彻底破坏。

试件E2 的主筋界面随加载开始脱粘，由于界面弹性模量的增大，跨中由弯曲拉应力引起的沿箍筋垂直向上的弯曲裂纹比试件E1 短，并且主筋上部由于剪切应力的作用开始萌发斜裂纹。与此同时，主筋与箍筋的连接处由于弯曲拉应力的作用，开始萌发沿箍筋向上的弯曲裂纹，如图3（b）的Step-242所示。当加载到274步时，主筋上部的斜裂纹和沿箍筋向上的弯曲裂纹同时向上扩展，如图3（b）的Step-274 所示，破坏状态图上以弯曲裂纹、斜裂纹占主导地位。然后，弯曲裂纹、斜裂纹继续发展，最终如图3（b）的Step-420 所示。相较E1 试件而言，无论是沿箍筋向上的弯曲裂纹，还是沿主筋产生的由于界面破坏导致的裂纹，其长度都明显比E1 试件短。最后梁上部和内部混凝土被压碎，如图3（b）的Step-670所示。

试件E4 的主筋界面混凝土失稳破坏后，随着脱粘部分继续进行，破坏单元大量的出现，除了跨中由于弯曲拉应力作用产生的沿箍筋向上的裂纹外，其他地方没有宏观裂纹出现，如图3（c）的Step-242所示。在274加载步，由于主筋上下界面的破坏，在剪切应力的作用下主筋界面处萌发出了斜裂纹，随后在钢筋混凝土梁腹内形成了由剪切破坏产生的“八”字形裂纹，如图3（c）的Step-274所示。在“八”字形裂纹形成后，由于拉应力的作用在箍筋与主筋的连接处萌发了顺着箍筋向上的弯曲裂纹，保护层混凝土也多处被拉裂，如图3（c）的Step-420 所示，此时破坏状态图中的裂纹与变形主要出现在跨中部位，且为斜裂纹。之后，梁上部和内部混凝土被压碎，如图3（c）的Step-670。

图3 不同界面弹性模量的钢筋混凝土梁试件的破坏过程图Fig.3 Failure process of reinforced concrete beams with different interface elastic modulus

文献［19］在静载作用下，利用二维数值模拟软件对不同界面弹性模量的钢筋混凝土梁在三点弯曲作用下的破坏过程进行了数值模拟研究。文献［19］中分析了界面弹性模量分别为0.1 GPa、1 GPa、7.5 GPa的试件，依次表示为L-0.1、L-1、L-7.5，它们最终的破坏模式如图4 所示。研究结果表明，界面弹性模量较低时，破坏模式以弯曲裂纹、顺筋裂纹占主导地位；界面弹性模量适中时，破坏模式以弯曲裂纹、斜裂纹占主导地位；界面弹性模量较高时，破坏模式以斜裂纹占主导地位。

图4 静载下不同界面弹性模量梁的破坏状态［19］Fig.4 Failure modes of numerical simulation beams with different interface elastic modulus under static loading[19]

将L-0.1、L-1、L-7.5 的最终破坏模式分别与本文试件E1 的第274 步、试件E2 的第274 步、试件E4 的第420 步的破坏模式相比较，可以发现它们极为相似，这说明动载作用下界面弹性模量变化对三点弯曲梁试件的影响和在静载作用下的影响规律是相似的。

混凝土材料破坏时会产生声发射（Acoustic Emission，简称AE），从微观机制看，声发射是脆性（准脆性）材料微裂纹以及结构面在破坏过程中能量的释放。混凝土的单元损伤数与声发射次数成正比，图5 所示为梁试件E1、E2、E4 的声发射数-加载步柱状图。E1、E2、E4 的AE 图均存在着4 个极值点。1 号极值点是由于梁试件E1、E2、E4 预留裂缝处的应力集中使得钢筋混凝土下部开裂导致。2 号极值点是因为梁试件E1、E2、E4 下部纵筋界面混凝土破坏导致。而对于3 号极值点，试件E1 主要是由于在混凝土中产生了弯曲裂纹所导致，试件E2 主要是由于在混凝土中产生了弯曲裂纹和斜裂纹共同作用所导致的，试件E4 则是由于在混凝土中产生了斜裂纹所导致。4 号极值点的出现则是因为试件E1、E2、E4 的上部混凝土被压碎而导致大量声发射的发生。

图5 加载步-声发射数柱状图Fig.5 Loading step-AE histogram

声发射累计数（Accumulative Acoustic Emis⁃sion，简称AAE）能反映材料在破坏过程中能量的耗散情况，并且声发射累积数与材料的能量释放值成正比，可以从能量角度反映材料在破坏过程中所表现出来的延性。由图6 可知，E4 的AAE 数最大，破坏过程中能量的释放量主要跟试件损伤破坏的单元数量有关，故而E4 的单元损伤破坏最严重。在图6 中，从试件E1 至试件E5，梁的界面弹性模量由小到大。各梁所对应曲线的最大值，代表梁的耗能能力的强弱。随着界面弹性模量的逐渐增大，梁的耗能能力也随之逐步增强，试件E4 处耗能能力达到最强。之后随着弹性模量继续增加，耗能能力有所减小。说明梁的耗能能力随着界面弹性模量的增大，总体上呈现先增大后减小的趋势，梁的弹性模量存在着一个最优值，使得梁在破坏过程中的耗能能力达到最强。

由图6中E1的曲线图可观察到3个明显的“跳跃点”，分别对应的是图5 的第2、3、4 个极值点，与文献［20-21］中实验梁破坏过程的能量累计曲线中的突变点较为相似。图6 中，突变点JP1 对应梁下部混凝土在拉力作用下的开裂，此时钢筋和混凝土之间出现了相对滑动的趋势；突变点JP2 对应着界面混凝土的失稳破坏；突变点JP3 对应着钢筋肋间混凝土不断被压碎，同时受压区的混凝土也开始被压碎，最终导致梁的破坏。

图6 声发射能量累积曲线Fig.6 Acoustic emission energy accumulation curve

图7 为本文数值模拟的界面弹性模量-峰值荷载曲线。由图7可知，峰值荷载随界面弹性模量的变化呈现出中间高两边低的趋势，其中试件E1 最低。由于文献［6］得到了钢纤维混凝土界面弹性模量随水灰比的增大而减小的结论，因此文献［22］的物理实验结果实际上反映的是界面弹性模量对试件承载力的影响，文献［22］的研究结论认为材料的弯曲强度随着水灰比的变化也呈现中间高两边低的现象，与本文的研究结论一致。梁的承载力最小值在最低界面弹性模量时取得，梁的承载力随界面弹性模量的增大而增大，但当界面弹性模量增大到一个最优值后，梁的承载力随着界面弹性模量的继续增大反而开始减小，即梁的承载力具有随着界面弹性模量的增大而先增大后减小的趋势，说明界面弹性模量存在着一个最优值，此时梁的承载力达到最大。