螺线式无针头静电纺丝过程中场强的分布与改善

刘延波 ，罗 鑫 ，郝 铭 ，刘 垚

（1.天津工业大学 纺织科学与工程学院，天津 300387；2.武汉纺织大学 纺织科学与工程学院，武汉 430200；3.武汉纺织大学 化学与化工学院，武汉 430200）

静电纺丝技术是一种简单而有效的制备聚合物纳米纤维的方法[1]，常规的静电纺丝装置被分为针头式与无针头式两种[2-6]。对于常用的针头式静电纺丝，即使人们可以通过改变针头形态而制备多组分纳米纤维[7]，但依然难以解决生产效率低、针头易堵、难以清理以及边缘效应（edge effect）问题[8-9]。基于液体自由表面重组原理[10]，人们逐渐开发出了各种不同类型的无针头静电纺丝装置来解决产量问题。例如捷克Elmarco 公司[11]开发出转辊式无针头静电纺丝头（纳米蜘蛛一代）；迪肯大学发明了螺旋线圈式无针头静电纺丝头[12]；捷克Elmarco 公司又开发了金属线型纺丝头（纳米蜘蛛二代）；上海云同纳米科技有限公司发明了螺旋叶片式无针头静电纺丝头等[13]。然而，无针头静电纺丝[14-16]设备同样存在难以克服的问题，例如所需电压较高导致空气击穿带来的着火和爆炸危险，开放式供液引起的溶剂快速挥发，纺丝液浓度逐渐增大，以及溶剂挥发以后，残留聚合物沉积在纺丝头表面引起纺丝头曲率半径逐渐增大、电场强度逐渐减小带来的纺丝质量前后不一致等问题。同时，无针头静电纺丝过程中同样存在边缘效应现象[17]，影响静电纺丝进一步的规模化[18]。

本文以迪肯大学发明的螺旋线圈式的无针头静电纺丝头为例，利用COMSOL Multiphysics 5.4 有限元分析软件对无针头式静电纺丝过程中场强大小和分布规律进行了仿真，研究了纺丝头结构参数包括螺旋线圈的长度、螺旋直径、螺旋螺距、金属丝线直径以及接收距离、纺丝电压等工艺参数对场强大小与分布的影响规律，继而根据场强分布规律对存在的边缘效应现象提出了改善措施，最后通过场强模拟对场强改善措施进行了评价，验证了所提出场强改善措施的合理性和可行性。本文的研究思路和方法在于为无针头静电纺丝技术的工业化实施和推广奠定基础。

1 建模与模拟

1.1 螺线式无针静电纺丝设备建模

图1 和图2 为螺线式无针静电纺丝设备的模型图，其具体规格与参数如表1 所示。纺丝设备模型的建立主要分为几步：首先新建零件，通过创建草图和插入曲线，按所需尺寸绘制螺旋线；再以螺旋线为路径，通过扫描功能得到螺线式纺丝头；然后再新建1个零件，对矩形草图进行凸台拉伸，得到接收板；同理，利用凸台功能构建空气界面模型；最后新建一个装配体，将纺丝头、接收板、空气界面这3 个零件按照几何关系组装。

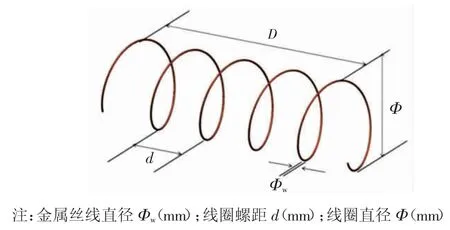
图1 螺旋线圈结构参数示意图Fig.1 Schematic diagram of structure parameters of spiral coil

图2 对照组的螺线式无针静电纺丝设备模型Fig.2 Spiral needle-free electrospinning equipment model of control group

表1 对照组的螺线式无针静电纺丝模型基本参数Tab.1 Basic parameters of spiral needleless electrospinning model of control group

1.2 螺线式无针静电纺丝的静电场模拟

1.2.1 COMSOL 静电场模拟原理

COMSOL Multiphysics 5.4 是一种典型的以有限元分析法为基础的模拟软件，通过求解偏微分方程近似解数值的方法，对真实的物理场系统进行模拟，从而解决多种复杂的问题。其模拟流程可归纳为：确定模拟项目→建立模型→设定求解与边界条件→划分网格→求解→后处理[19]。目前该软件可实现多种物理场的模拟，主要有：AC/DC、声学、化学物质传递、电化学、流体流动、传热、光学、等离子体、射频、半导体、结构力学和数学物理场。本文使用到的是COMSOL Multiphysics 5.4 软件中 AC/DC 模块内的静电（es）物理场对静电纺丝过程中的静电场进行模拟，静电场遵循泊松方程[20]：

式中：ε0表示真空介电常数；εr表示介质的相对介电常数；V 代表电势能；ρ 为空间电荷密度。此方程中各个变量都可在软件中选择设置具体数值。本课题的模拟中，ε0为 8.85 × 10-12F/m，ρ 为 0 C/m3，纺丝电极处的电势为20 kV，接收板和螺线式纺丝头的材料均选择金属（钢），εr为 1。

1.2.2 COMSOL 静电场模拟步骤

对对照组进行有限元电场模拟获得如图3 所示的电场图。

图3 对照组的螺线式无针纺丝头的电场云图与电场强度分布曲线Fig.3 Electric field cloud image and electric field intensity distribution curve of spiral needleless spinning head of control group

由图3 可知，螺线式纺丝头顶部，即靠近接收板这端的电场强度更大，电荷主要集中在每个单线圈的顶部，由此可知，静电纺丝过程中，射流一般在这些区域形成。为了进一步研究产生射流的区域的电场强度的大小和分布规律，在软件中沿着线圈轴向，导出靠近接收板一侧的线圈顶端的电场强度具体数值，可根据这些数据分析静电纺丝过程中电场强度的分布规律。

1.3 控制变量实验

设计控制变量实验，从线圈长度、线圈直径、螺距、金属丝直径、纺丝接收距离和施加电压6 个方面研究这些参数对电场强度分布的影响。在其他条件不变的情况下，只改变单因素的量，然后利用COMSOL Multiphysics 5.4 软件分别进行模拟，研究其电场强度大小及分布的情况。其中纺丝头结构参数作为变量时，纺丝电压均为20 kV，接收距离都是150 mm；某个纺丝工艺参数作为变量时，螺线式纺丝头的其他结构参数参见图题说明。限于篇幅，不再单独列出。

2 结果与讨论

2.1 螺旋线圈结构对纺丝头场强分布的影响

2.1.1 线圈长度对场强分布的影响

图4 为不同线圈长度的电场图。

图4 不同线圈长度的纺丝电极（螺旋线圈）的电场云图Fig.4 Electric field cloud diagrams of spinning electrodes（spiral coils）with different coil lengths

从图4 中电场云图的颜色变化可知，线圈长度越短，纺丝电极顶端的电场强度越大，但每个单线圈的场强存在较大差异。静电纺丝工艺中，为了确保制备纤维的均匀性，应选择在相同电压条件下，场强较大且均匀性较好的纺丝电极。图5 显示了具有不同线圈长度（分别为 120、160、200、240 mm）的螺线式纺丝头电场强度的大小分布情况，其中横坐标表示纺丝电极上的点距离空气界面最左侧的水平距离，纵坐标代表纺丝头顶端电场强度的数值。此外各点的场强平均值和CV 值如表2 所示。

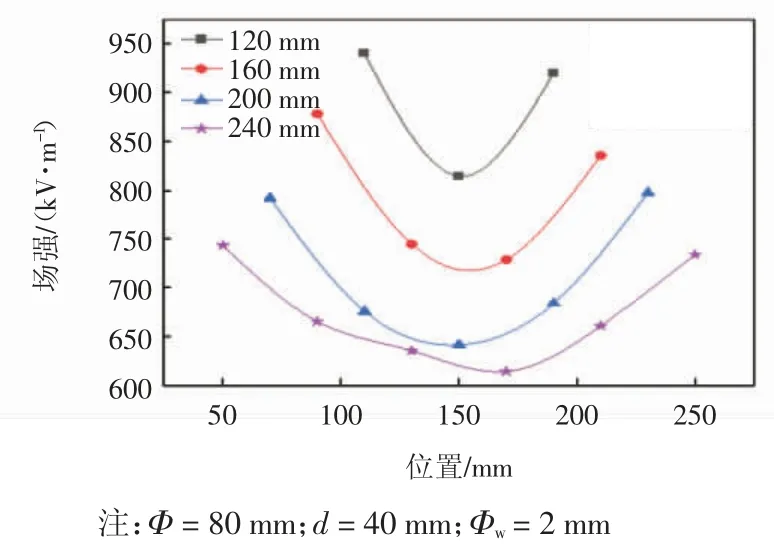
图5 线圈长度对纺丝头场强分布的影响Fig.5 Influence of coil length on field intensity distribution of spinning head

从表2 中的数据可以发现，随着线圈长度的增加，不仅纺丝头中间区域的电场强度逐渐下降，整个纺丝头的场强均匀性也在变化。可以看到当线圈长度为120 mm 时场强CV 值最小为7.57%，且此时场强平均值最大。虽然这种情况下纺丝电极的场强更均匀，有利于产生性能稳定的纤维，但由于圈数过小，产生的射流也减少，会直接影响产量。综合来看线圈长度为200 mm 时，场强平均值较大，且CV 值相对较小，该尺寸更适合纺丝。

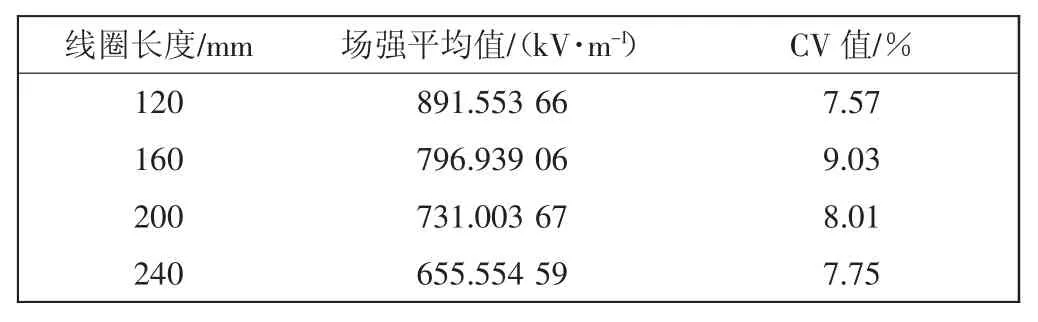
表2 线圈长度不同时纺丝头电场强度平均值和CV 值Tab.2 Average value of electric field intensity and CV value of spinning head with different coil length

2.1.2 线圈直径对场强分布的影响

图6 显示了具有不同线圈直径（40、60、80、100 mm）的螺线式纺丝头的电场强度分布，纺丝头顶端的电场强度平均值和CV 值如表3 所示。

图6 线圈直径对纺丝头场强分布的影响Fig.6 Influence of coil diameter on field intensity distribution of spinning head

表3 线圈直径不同时纺丝头电场强度平均值和CV 值Tab.3 Average value of electric field intensity and CV value of spinning head with different coil diameters

随着线圈直径的增加，线圈顶端的电场强度逐渐下降。在物理学中，不规则形状导体表面的电荷主要集中在凸起区域，在其他条件相同的情况下，曲率大的部分电荷密度较高，纺丝头的线圈直径越小，曲率越大，因此场强更高。由表3 可以看出，场强CV 值随着线圈直径的增加呈先下降后上升的趋势，且发现线圈直径为60 mm 时，场强均匀性最佳，且场强平均值较高。

2.1.3 螺距对场强分布的影响

图7 显示了具有不同螺距（10、20、30、40、50 mm）的螺线式纺丝头的电场强度分布。纺丝头顶部的电场强度平均值和CV 值如表4 所示。

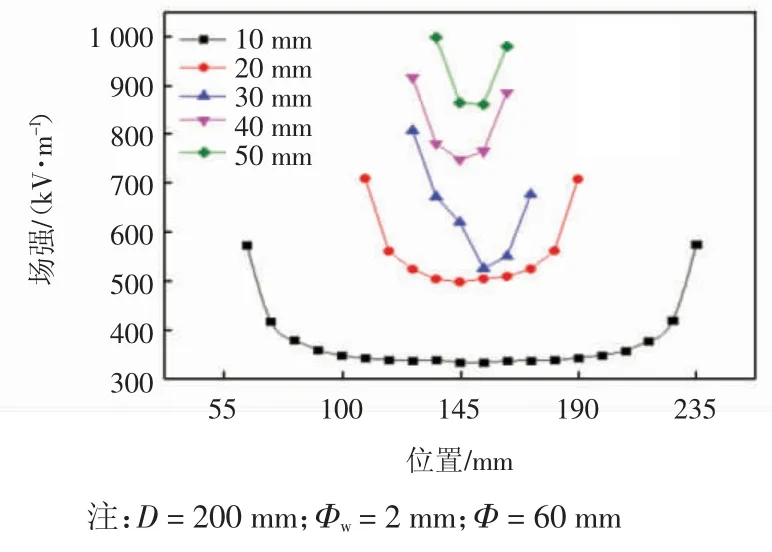
图7 螺距对纺丝头场强分布的影响Fig.7 Influence of pitch on field intensity distribution of spinning head

表4 螺距不同时纺丝头电场强度平均值和CV 值Tab.4 Average value of the electric field intensity and CV value of spinning head with different pitches

由图7 可知，当螺距从10 mm 增加至50 mm 时，纺丝头的电场强度变化极大，随着螺距的增加，纺丝头的电场强度逐渐增强。这是由于各线圈之间电场强度相互干扰，螺距越大则螺旋线圈的圈数越少，线圈受到的干扰也会减少，于是场强随之增加。但无论螺距如何变化，纺丝头的电场强度始终遵循两端高，中间低的规律。另外，由表4 可知，螺距对场强均匀性的影响非常大，随着螺距的增大，电场强度均匀性迅速增强，因此增大螺距是快速提升场强均匀性的有效方法。但较大的螺距会导致纺丝过程中接收板收集到的纤维相隔较远，破坏了纤网的均匀性，产生的射流个数减少，纤网很容易出现明显的两边厚中间薄的现象。所以，虽然根据模拟数据可以推测出，如果继续增大螺距，场强CV 值会继续下降，但为了保证纤维的产量与质量，不可无限制地增加螺距。综合来看，螺距为40 mm 时场强平均值较高，相对均匀，且有利于生产更多纤维。

2.1.4 金属丝直径对场强分布的影响

图8 显示了具有不同金属丝直径（1、2、3、4 mm）的螺线式纺丝头的电场强度分布，纺丝头顶端的电场强度平均值和CV 值如表5 所示。

表5 不同金属丝直径的纺丝头电场强度平均值和CV 值Tab.5 Average value of electric field intensity and CV value of spinning head with different metal wire diameter

图8 金属丝线直径对纺丝头场强分布的影响Fig.8 Influence of wire diameter on field intensity distribution of spinning head

由图8 以及表5 可知，螺旋线圈的金属丝直径越细时，纺丝头的电场强度越高，场强均匀性越佳，场强平均值也越高。这是由于在其他条件不变的情况下，金属丝直径的增加必然会导致纺丝头的整体体积也随之增大。因此本文选择金属直径为1 mm 的参数。

2.2 纺丝工艺参数对纺丝头场强分布的影响

2.2.1 施加电压对场强分布的影响

由于电压是激发带电射流并且在静电纺丝过程中拉伸射流形成纤维的主要原因，因此电压是对静电纺丝过程电场强度分布非常重要的影响因素。施加的电压值为20～50 kV 时纺丝头的电场强度随电压变化的趋势如图9 所示。

图9 电压对纺丝头场强分布的影响Fig.9 Influence of voltage on field intensity distribution of spinning head

由图9 可知，纺丝头线圈顶端的电场强度随着电压的增大呈增长趋势，适当增加电压不但有利于纤维的成型以及细化，还可以有效提升纤维的产率。但在实际生产中电压不可过高，否则容易引发火灾。由此可知，需要选择一个合适的电压范围才能生产出符合工艺要求的纤维。

此外，表6 为不同电压条件下纺丝头的场强CV值。

表6 电压不同时纺丝头电场强度平均值和CV 值Tab.6 Average value of electric field intensity and CV value of spinning head with different voltages

由表6 可知，电压的变化对静电纺丝过程中电场强度均匀性的影响不大，这说明电场强度随电压的变化是符合线性增长规律的（拟合曲线方程为：E =398 446 8+398 471U，R2=1），当电压升高时，虽然电场强度随之升高，但CV 值较稳定。这可能是由螺线式纺丝电极的特殊结构导致的，纺丝电极中，线圈有一定的倾斜角度，且螺旋线圈整体贯连，并非是一个个无连接的金属圆圈。

2.2.2 纺丝接收距离对场强分布的影响

接收距离主要对射流在电场中停留时间的长短和场强的大小造成影响，进而影响溶剂的挥发速率。距离过短时，射流没有足够的停留时间，导致溶剂未能完全挥发，纤维间相互粘结而不是形成理想的均匀纤维网；距离过长时则会导致场强过低，容易引发纺丝头堵塞。图10 为电场强度随接收距离变化的模拟结果，不同接收距离条件下纺丝头顶端的场强平均值和CV 值如表7 所示。

表7 接收距离不同时纺丝头电场强度平均值和CV 值Tab.7 Average value of electric field intensity and CV value of spinning head with different receiving distances

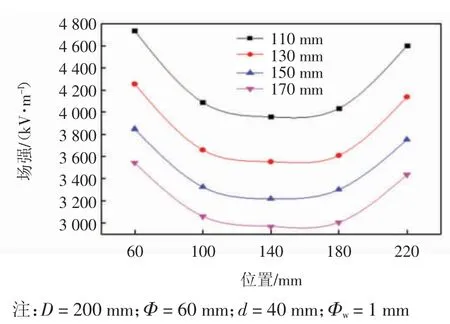
图10 接收距离对纺丝头场强分布的影响Fig.10 Influence of receiving distance on field strength distribution of spinning head

由图10 可知，纺丝头电场强度的大小随着接收距离的增加而减小。根据库仑定理可知，两个点电荷之间的作用力随着点电荷间距的增大而减弱，从表7看出随着接收距离的增加，场强平均值在下降，从对电场强度大小的影响方面来讲，接收距离的变化对纺丝头场强分布均匀性的影响不是很明显。这可能是由于纺丝头的场强均匀性主要是受到线圈之间电场叠加效果的影响，而接收距离的变化对线圈之间库伦斥力影响较小，场强均匀性变化也较小。

在实际的纺丝实验中，接收距离还要根据聚合物溶液的性质，溶剂的挥发性等因素来确定，通过缩小接收距离以获得更大场强的同时要考虑到带电射流的状态，如果接收距离太短，容易导致溶剂挥发不完全，甚至射流牵伸不充分，纤维无法固化成型，影响纤网形貌特征。

2.3 纺丝头结构的参数优化结果

螺线式无针静电纺丝过程中，纺丝电极结构的参数对静电纺制备的纤维影响很大，通过之前的数据可知，理论上讲，线圈长度D 为200 mm，线圈直径Φ 为60 mm，螺距 d 为 40 mm，金属丝直径 Φw为 1 mm，为纺丝头结构的最优参数。将参数优化后的螺线式纺丝头在外加电压为50 kV，接收距离为150 mm 时进行静电场模拟，电场强度分布状况如图11 所示，此外纺丝电极的场强平均值为1 818.570 27 kV/m，场强CV 值为7.08%。

图11 最佳参数纺丝头的电场场强分布Fig.11 Electric field intensity distribution of the optimal parameter of spinning head

由于边缘效应现象的存在，使得螺旋线圈式纺丝头两侧场强高于内侧，特别是纺丝头中间部分场强最低，纺丝射流的发射会受到抑制，而两侧的纺丝射流会很强且向外侧喷射，造成飞花（flies）现象、浪费原料。于是考虑在纺丝头左右两侧分别增加一小段直径逐渐缩小的螺旋线圈作为辅助电极，如图12（a）所示，以便降低两侧的电场强度，可中和或消除边缘效应现象，使电场强度及纺丝射流沿幅宽方向分布更加均匀。

图12 和图13 分别为场强云图和数据分布。

图12 辅助电极优化的纺丝头模型和电场云图Fig.12 Spinning head model and electric field cloud diagram optimized for auxiliary electrode

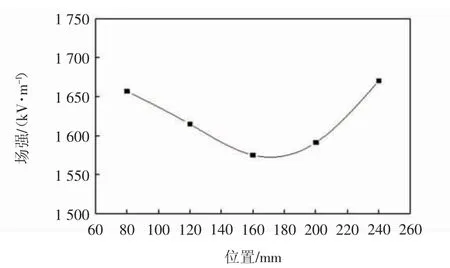
图13 辅助电极优化纺丝头的场强分布Fig.13 Spinning head field intensity optimized for auxiliary electrode distribution

根据图12（b）和图13 可知，增加辅助电极后纺丝头的电场强度均匀性有所改善，虽然场强平均值为1 621.580 38 kV，相较而言略微下降了，但场强CV 值下降至2.53%，变化非常大。这说明添加辅助电极对电场强度均匀分布的效果非常好，辅助电极使纺丝头两端受到来自两侧的电场叠加，可以有效地缓解边缘效应现象，有利于生产直径更均匀的纤维。

3 结 论

（1）本文基于螺旋线圈式结构模型、利用有限元分析技术研究了无针头电纺中场强分布规律，系统模拟了纺丝头结构参数和静电纺丝工艺参数对场强分布的影响，并据此提出了改善场强边缘效应的措施，也即在无针头纺丝头两侧采用直径逐渐变小的渐变纺丝头直径（相当于增加辅助电极），获取了最优纺丝头结构模型。

（2）优化纺丝头结构参数为：线圈长度200 mm，线圈直径60 mm，螺距40 mm，金属丝线直径1 mm，此时纺丝头在静电场中电场强度平均值较高且分布均匀。

（3）进一步的场强模拟结果表明，当外加电压为50 kV、接收距离为150 mm 时，此时纺丝电极的场强平均值为1 621.580 38 kV/m，场强CV 值可降至2.53%，有效降低了静电纺丝过程中的边缘效应。