基于自适应反步滑模的AUV推进器容错控制

张瀚文,王俊雄

基于自适应反步滑模的AUV推进器容错控制

张瀚文,王俊雄

(上海交通大学 船舶海洋工程国家重点实验室,上海,200240)

为了实现自主水下航行器(AUV)在推进器故障的情况下对运动控制的鲁棒性要求,针对AUV的六自由度非线性矢量运动模型,设计了自适应反步滑模运动跟踪控制器,并在推力分配中考虑推进器故障特点,建立连续时变的故障模型。结合故障信息,基于伪逆法技术,在调节控制器配置结构功能的基础上增加了对故障的调节功能,可以通过更改控制输入对故障进行修正,对不同的故障类型分别采取故障调节和控制重构的方法实现推进器故障状态下的容错控制,有效提高了容错控制算法的应用普适性。在仿真中,通过模拟多种不同的故障模式,验证了自适应容错控制器在推进器故障情况下对AUV运动控制的有效性。

自主水下航行器; 推进器; 自适应控制; 故障调节; 容错控制

0 引言

作为一种探测海洋的有效手段,水下航行器具有广泛的应用前景,可完成探测、水下作业和特种作战等任务。传统的自主水下航行器(autono- mous undersea vehicle,AUV)主要完成长距离巡航的任务,为了降低能耗,多采用欠驱动的细长回转体结构。随着作业要求的提高,全驱动AUV展现出了丰富的应用前景。多推进器的布置可以得到更丰富的控制输入,实现更复杂的任务要求,还为控制提供了冗余。但推进器的增多也意味着故障率的增加。深海环境下,一旦发生故障,作业任务会受到影响,机器人可能无法回收,造成巨大损失。因此,为提高AUV可靠性,如何对推进器进行故障诊断,并根据故障情况重构控制输入实现容错控制是迫切需要解决的问题。

容错控制方法可分为被动容错控制和主动容错控制。被动容错控制采用不变的控制器保证闭环系统对特定的故障具有鲁棒性。AUV作为一个高度非线性、强耦合以及有非匹配不确定性的系统,传统的线性方法如比例-积分-微分(proportion integration differential,PID)控制、线性二次型调节器(linear quadratic regulator,LQR)控制等已无法满足高精度的控制要求,目前国内外学者多采用反步法[1]、滑模控制[2-3]、鲁棒控制[4-5]、神经网络控制[6]等非线性控制和智能控制方法。Campos等[7]研究了一种用于AUV航路点跟踪和轨迹跟踪控制的基于变参数饱和函数的非线性控制器。边信黔等[8]为实现AUV在未知海流干扰作用下的地形跟踪控制,提出一种基于非线性迭代滑模增量反馈的航迹跟踪控制器,在实现对外界扰动较强鲁棒性的同时保证了跟踪控制系统的全局渐进稳定性。但这些研究均是基于某种控制方法设计控制输入达到被动容错控制的目的,对故障容错的自适应能力非常有限,在推进器故障严重时控制器可能会失效。

主动容错控制是在故障发生后基于故障信息,针对性地对控制器参数重新调整或改变结构,采取有效的容错策略达到降低故障危害的效果[9]。目前对AUV的容错控制研究多采用主动容错控制。Arslan等[10]针对 AUV 舵和尾鳍失效的情况,研究了一种最优控制方法,但这种方法只考虑单一的故障模式,控制效果受限。Podder等[11]将推力分配的优化思想,利用推进器的冗余来实现容错控制。但上述研究只考虑了推进器完全故障的极端模式。在实际运行时,AUV的推进器还会出现涌堵、转速波动等部分失效的情况,故障模型不够全面,不具代表性。Cristofaro等[12]介绍了在过驱动系统中使用未知输入观测器进行故障检测、隔离和控制重构。Dos Santos等[13]提出了一种基于虚拟推力器的AUV容错控制方法,该方法研究了位于不同作用平面的推进器部分故障或完全故障情况下,在伪逆法中通过分配矩阵计算水平推进力,并采用修正的加权矩阵,然后利用虚拟力计算出剩余工作推进器的合力,再投影到位于相同作用平面的剩余推进器的力,同时使用另外一组控制器来针对故障重新配置控制器,从而提高性能。

目前,关于AUV的主动容错控制较多从其动力学模型出发,通过调节推进器控制矩阵的参数实现容错控制[14-15]; 还有的方法根据故障情况选择对应的控制器组,实现容错控制。这些方案的本质都是通过更改控制方法本身来调节控制输入,而通过直接更改控制输入的方式实现容错控制的研究却较少。后者可避免对控制方法的更改,保证了系统的稳健性,提高了应用的普适性。

基于以上分析,文中以BLUE ROV模型为对象,研究推进器故障情况下的AUV容错控制问题。首先根据模型参数建立了六自由度的矢量化非线性运动模型,针对运动控制问题,基于自适应反步法设计运动控制器,引入滑模项克服模型的不确定性。在推进器的推力分配中,建立连续时变的推进器故障模型,再根据故障信息,针对推进器故障类型更改控制输入和控制器配置,设计自适应的容错重构方案。最后通过模拟工况仿真,验证不同故障形式下容错运动控制器的可行性和有效性。

1 AUV非线性模型

1.1 运动学-动力学模型

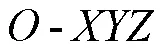
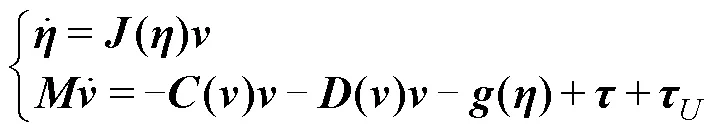
图1 AUV坐标系定义

Fig. 1 Coordinate system definition of an AUV

1.2 推进器模型

如图2所示,该AUV共有6个推进器,其中水平面上有4个,呈45°对角布置; 垂直面上有2个,沿着中心面对称布置。

图2 推进器布置

AUV的控制力主要是通过推进器的推力组合产生的,推进器螺旋桨由驱动电机控制,当AUV低速运动时,可采用以下模型

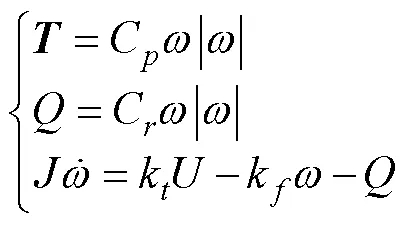
螺旋桨负载力矩与恢复力矩和偏心力产生的力矩相比,数量级很小,忽略其对控制输入的影响,推进器产生的组合控制输入可以表示为

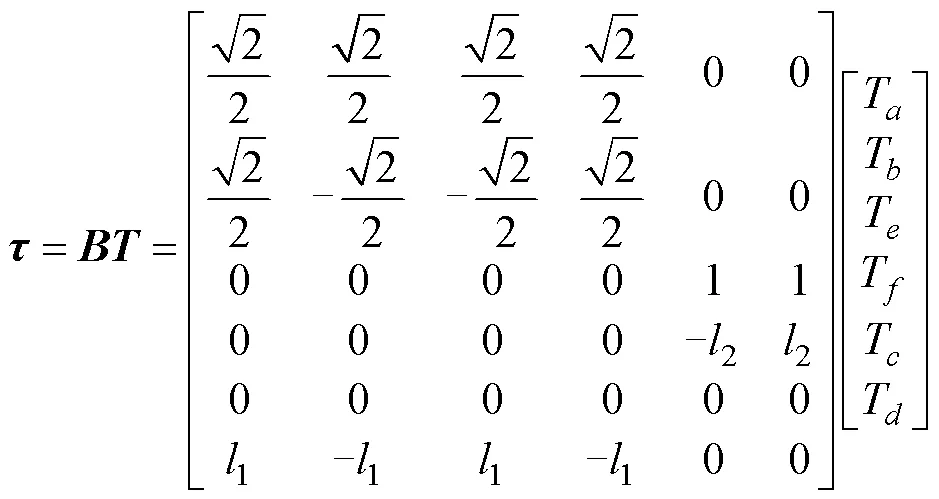
可以发现,AUV的俯仰通道无直接的控制输入,无法直接控制。由于AUV在恢复力的作用下可以实现自稳,因此假设俯仰角在运动过程中自稳并保持不变[17]。

2 运动控制器设计

2.1 自适应反步滑模运动控制器

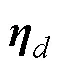
首先对AUV模型进行如下假设:

定义轨迹跟踪误差

选取第1个Lyapunov函数

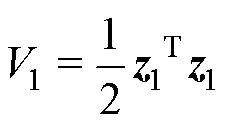
求导有

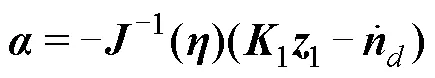
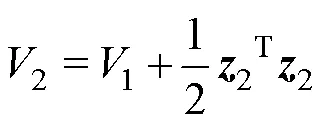
将式(5)和式(7)代入式(8)并求导

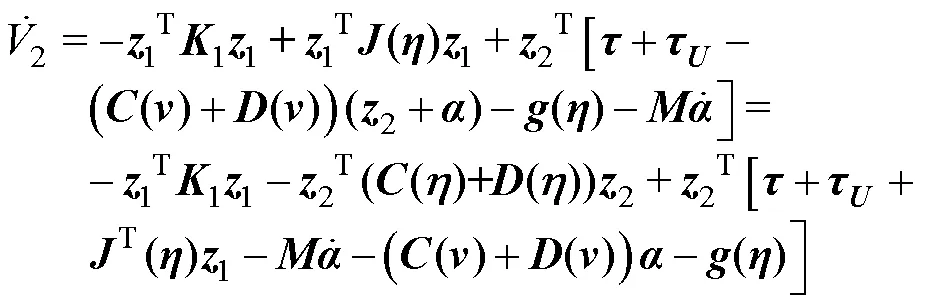
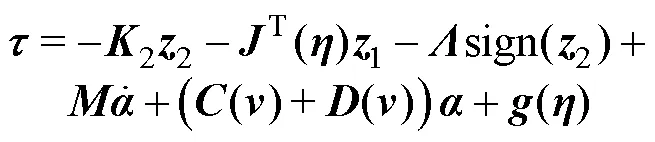
将控制输入式(10)代入式(9),可得到

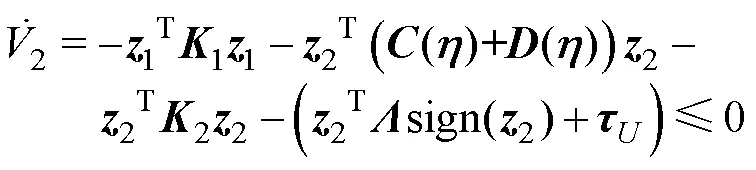
跟踪误差是渐进稳定的,因此该控制器可实现AUV的运动跟踪功能。

由于滑模项的引入,控制输入会出现不连续性,从而导致抖振问题。在这里采用一种具有动态边界层的饱和函数sat代替符号函数sign。

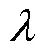
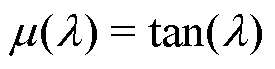
基于该边界层厚度函数,可以得到动态边界层的饱和函数[20]

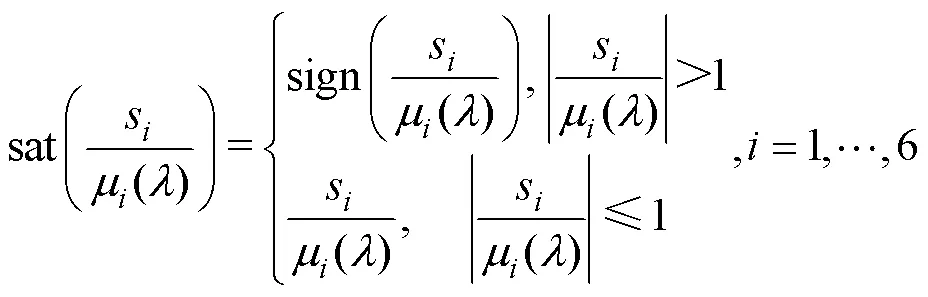
将式(13)代入式(10),可得到控制器输出

2.2 容错推力分配控制器

由于水下环境复杂,AUV推进器工作时很容易出现故障,如螺旋桨因水草附着引起不同程度的涌堵、螺旋桨卡死等,并且这些故障情况可能是连续出现的。在这里建立故障模型: 当螺旋桨出现拥堵故障时,相同激励电压下螺旋桨转速呈比例衰减,输出推力也会出现衰减; 当螺旋桨出现卡死故障时,螺旋桨电机短路损坏,电压和转速均变为0。

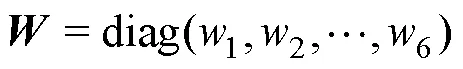
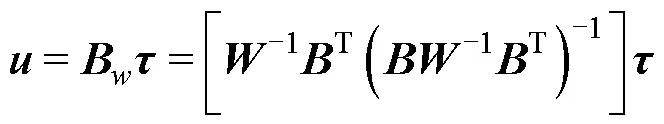
假设故障在任务期间发生且能被检测到,除卡死情况,仍能通过调整电压进行控制[24]。在检测到故障后,结合权重矩阵,修改控制器的输出来调整推进器的输出,使其恢复正常。

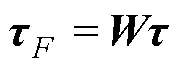
将式(16)代入式(15),可以得到修正后各推进器的分配量

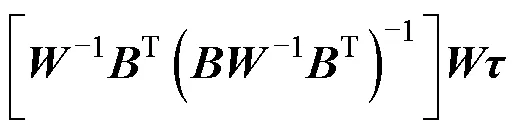
再基于推进器的故障情况,其实际输出量为

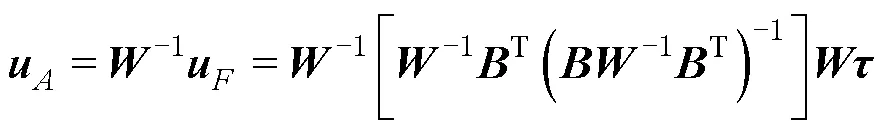
综上,所采用的推力分配控制器可以根据不同的故障类型,通过权重矩阵实时自适应地调整输入量或者修改控制器配置,实现推力重构。

3 故障模式与容错运动仿真

3.1 仿真条件和故障模式

模拟在水下自主巡逻时的状态,AUV的模型参数和控制参数为

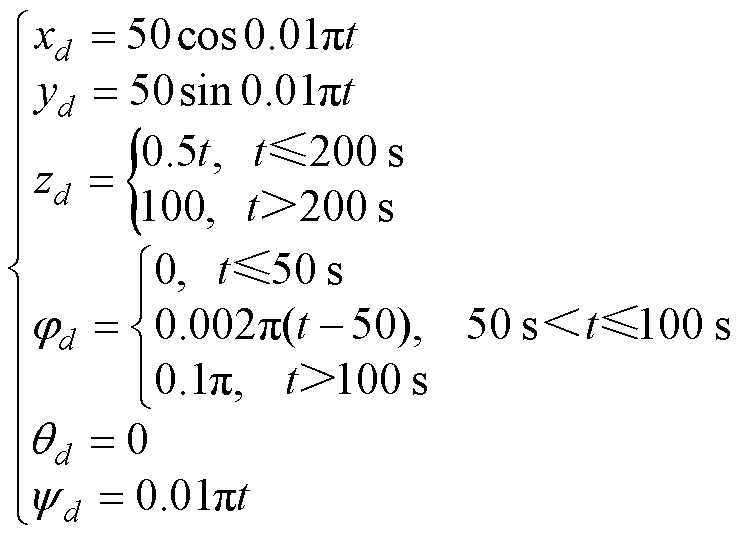
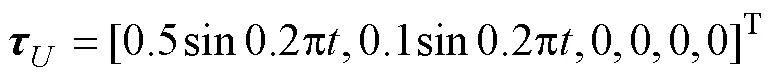
表1 推进器故障状态表

3.2 仿真结果与分析

仿真的数据结果如图3～图8所示。图3的三维轨迹仿真结果可以直观地看出有无容错控制器对轨迹跟踪的影响。在运动的初始阶段,可以发现两者都能对目标轨迹进行跟踪。原因是滑模运动控制器具有一定鲁棒性,对故障造成的推力衰减可以将其转换为外界的扰动进行处理,利用滑模项克服故障的影响。因此,当推进器的故障情况还不严重时,仅依靠运动控制器的鲁棒性,也可以实现运动控制的任务。而在后期的轨迹中,随着故障情况的加剧,单纯依靠滑模控制器无法有效应对推力分配的紊乱情况,无容错控制的AUV逐渐偏离目标轨迹。

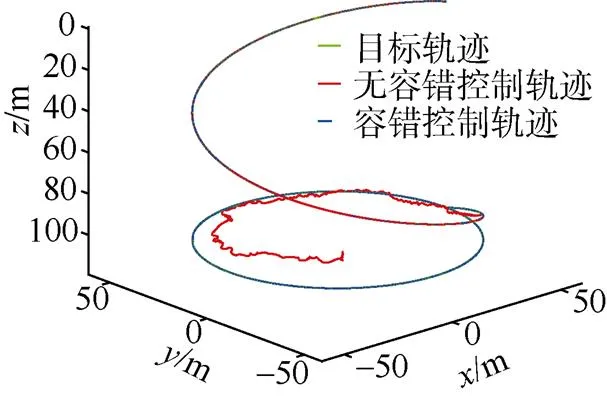
图3 AUV三维运动轨迹

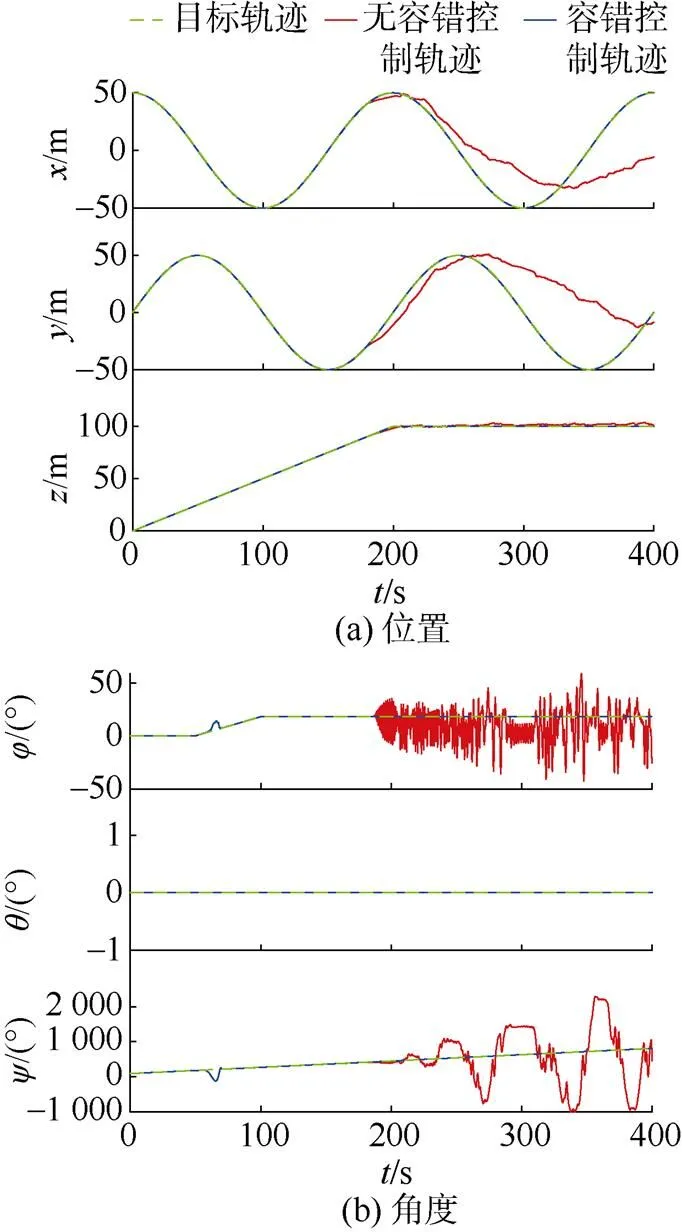
图4 六自由度状态量

进一步分析图4和图5的数据可以发现,在160 s前,两者都能很好地跟踪目标轨迹。而随着推进器故障加剧,无容错控制轨迹的跟踪误差开始发散,无法收敛,AUV无法完成轨迹跟踪任务。而结合容错重构算法的控制器对故障展现出了很好的鲁棒性,在不同的故障情况下仍能保证跟踪误差的收敛稳定性。通过图6分析可知,采用容错控制器后,即使推进器发生了故障,容错推进器也能够及时调整推进器的输出,对总控制输出进行重构恢复,实现期望的组合输出推力和力矩,完成循迹任务。

通过图7和图8展示的各推进器推力调节过程发现,在推进器出现故障时,容错控制器能根据故障情况及时调整推力分配权重,并通过螺旋桨电机的电压对推进器输出进行调节,补偿故障情况,恢复推进器输出。当有推进器出现完全故障时,容错控制器也能利用推进器的冗余度,及时调节剩余冗余推进器的电压,重构控制输出。

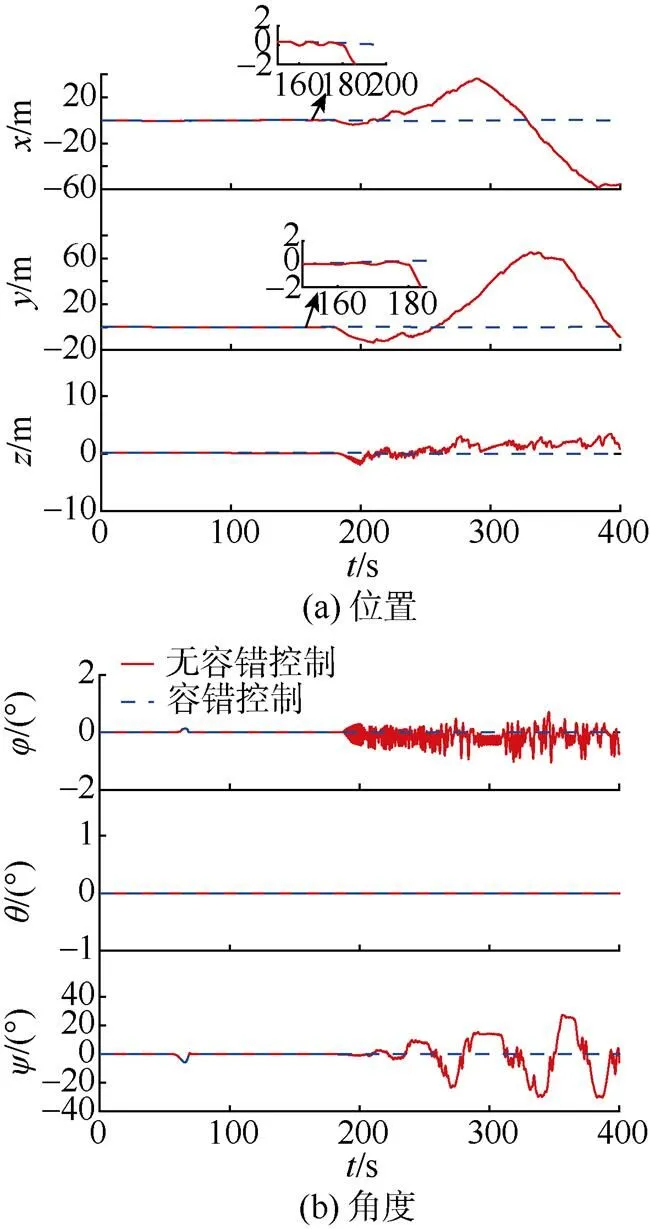
图5 轨迹跟踪误差

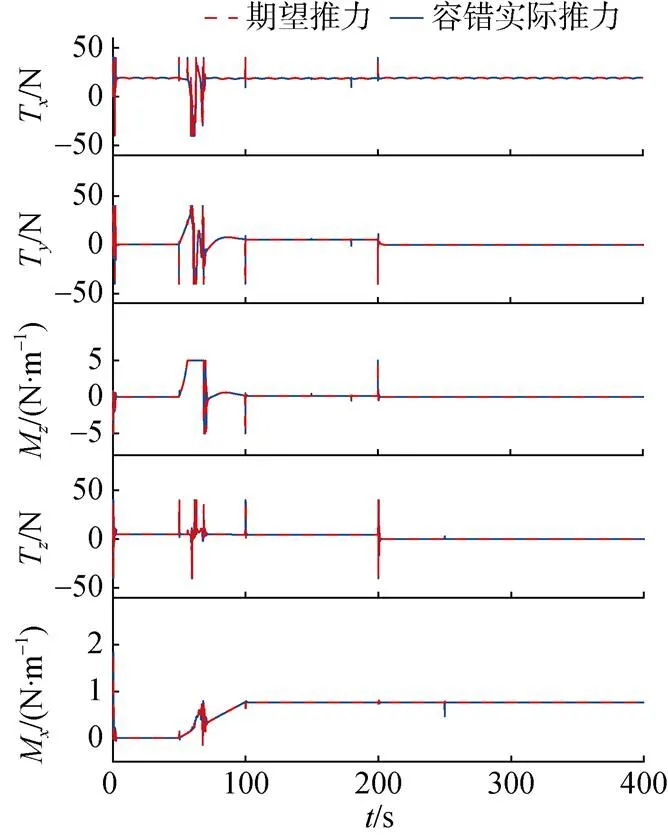
图6 推进器组合输出推力

综上,该容错控制器能有效应对不同推进器的故障情况,通过推进器的故障调节和冗余配置,完成AUV系统推进器的故障容错运动控制任务。

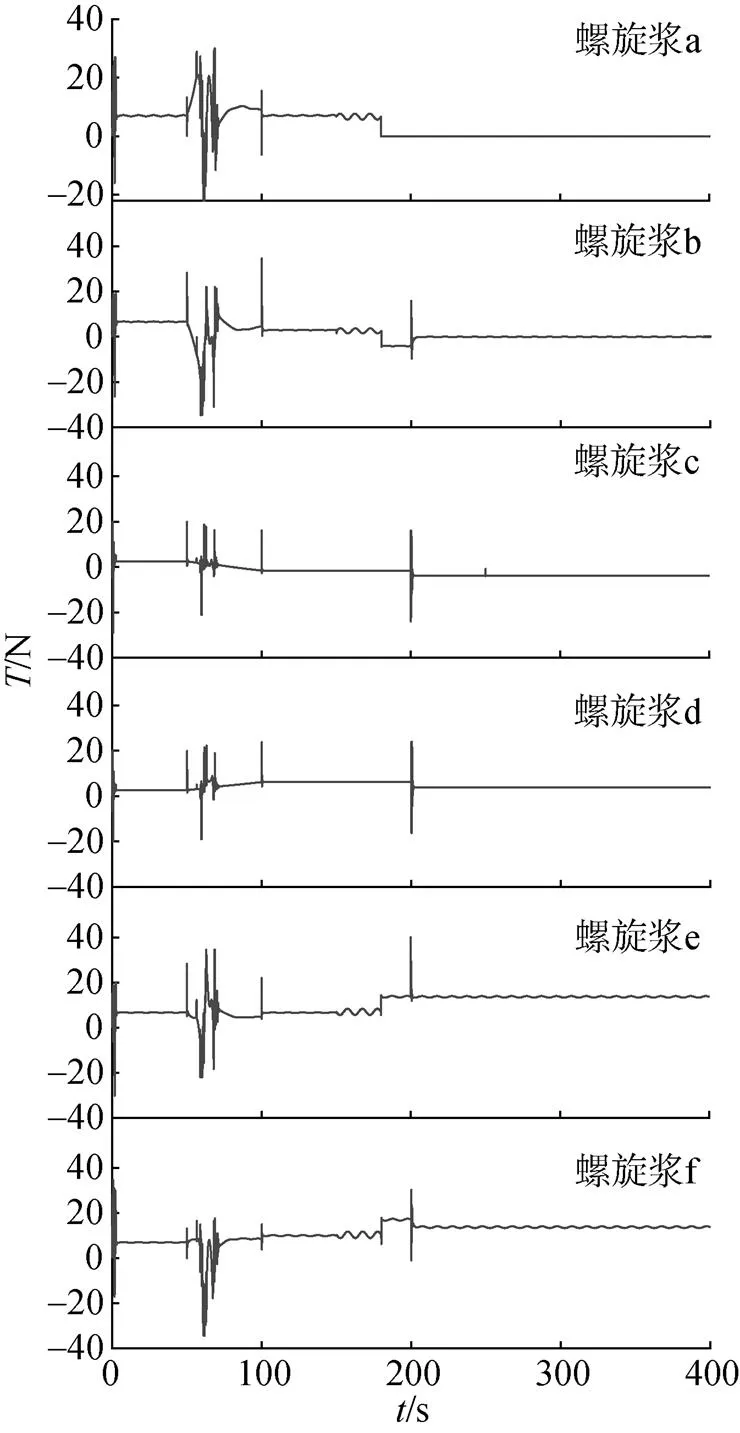
图7 螺旋桨推力

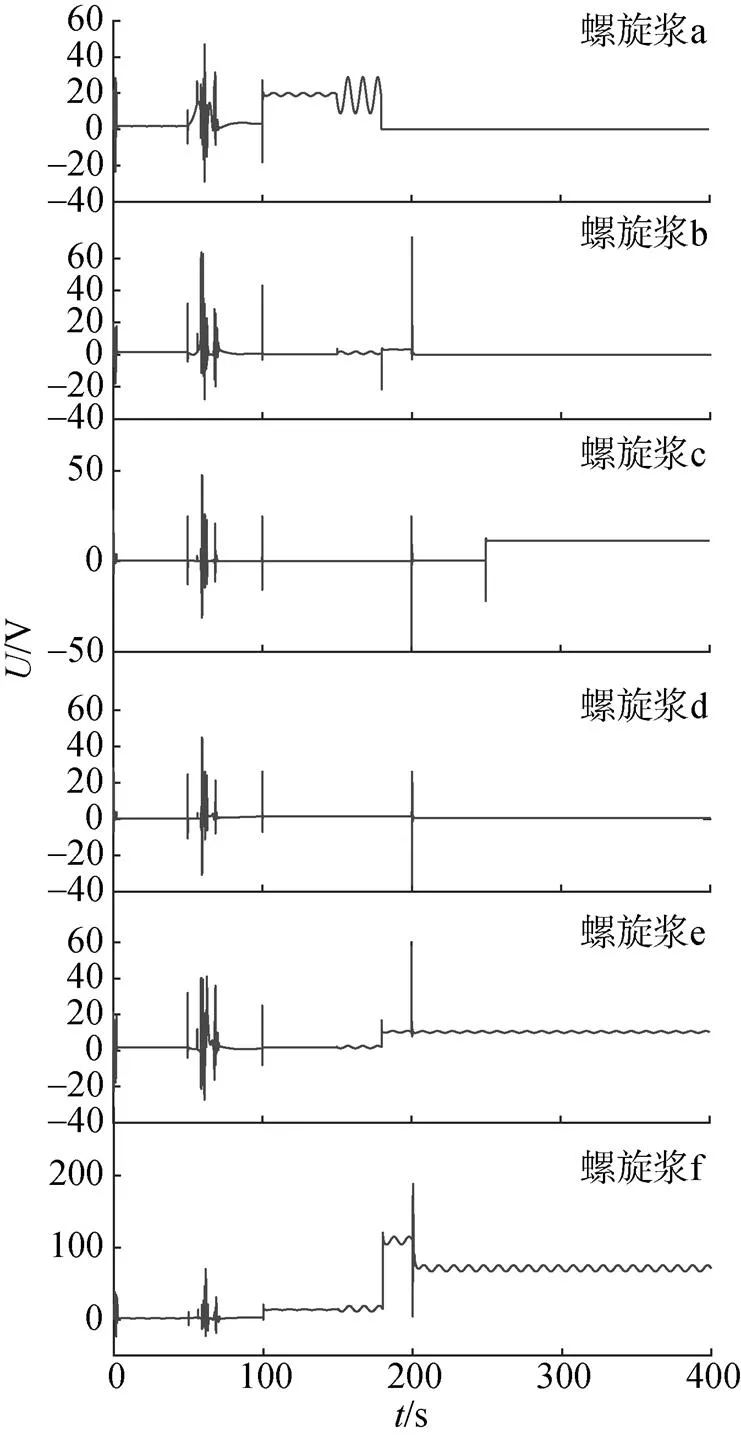
图8 螺旋桨电机电压

4 结束语

针对AUV推进器连续时变故障,文中提出一种基于自适应反步滑模的运动控制方法结合伪逆重构算法的推力分配方法,其可以自适应地调整推力分配策略,实现容错控制,完成轨迹跟踪任务。仿真结果表明,该控制算法可有效应对推进器出现的不同故障情况,利用故障信息对控制推力进行快速重构,对外界扰动和推进器故障具有鲁棒性,可以实现干扰下AUV的推进器容错运动控制。相比其他容错控制方法,文中所采用的动态冗余法和静态冗余法相结合的主动容错控制方法,在故障推进器仍然可控时,基于故障诊断信息修改控制器的输入,使得推进器的输出恢复正常。而当推进器完全故障不可控时,再基于故障诊断信息,更换控制器配置,通过冗余的推进器完成推力分配,实现推力重构,有效提高了容错控制算法的应用普适性。未来将继续丰富故障类型并完善控制器设计,进一步提高AUV对故障的容错能力。

[1] Xiao L,Qu X,Lei W,et al. Three-Dimensional Path Following of an Underactuated AUV Based on Fuzzy Backstepping Sliding Mode Control[J]. International Journal of Fuzzy Systems,2017,20(1): 1-10.

[2] 施小成,周佳加,边信黔,等. 模糊滑模变结构控制在AUV纵倾控制中的应用[J]. 计算机仿真,2008,25(10): 174-177.

Shi Xiao-cheng,Zhou Jia-jia,Bian Xin-qian,et al. Simulation of Fuzzy Sliding-Mode Control for AUV Pitch Control[J]. Computer Simulation,2008,25(10): 174-177.

[3] Chu Z,Xiang X,Zhu D,et al. Adaptive Fuzzy Sliding Mode Diving Control for Autonomous Underwater Vehicle with Input Constraint[J]. International Journal of Fuzzy Systems,2018,20:1460-1469.

[4] Lucia M. H2 and H∞Designs for Diving and Course Control of an Autonomous Underwater Vehicle in Presence of Waves[J]. IEEE Journal of Oceanic Engineering,2008,33(2): 69-88.

[5] 刘旌扬,冯正平,易宏,等. 水下机器人H∞控制系统设计[J]. 海洋工程,2008,26(3): 70-77.

Liu Jing-yang,Feng Zheng-ping,Yi Hong,et al. Design of H∞Control System for Autonomous Underwater Vehicles[J]. The Ocean Engineering,2008,26(3): 70-77.

[6] Cui R,Yang C,Li Y,et al. Adaptive Neural Network Control of AUVs with Control Input Nonlinearities Using Reinforcement Learning[J]. IEEE Transactions on Systems,Man,and Cybernetics: Systems,2017,47(6): 1019- 1029.

[7] Campos E,Monroy J,Abundis H,et al. A Nonlinear Controller Based on Saturation Functions with Variable Parameters to Stabilize an AUV[J]. International Journal of Naval Architecture and Ocean Engineering,2019,11(1): 211-224.

[8] 边信黔,程相勤,贾鹤鸣,等. 基于迭代滑模增量反馈的欠驱动AUV地形跟踪控制[J]. 控制与决策,2011,26(2): 132-135,139.

Bian Xin-qian,Cheng Xiang-qin,Jia He-ming,et al. A Bottom-following Controller for Underactuated AUV Based on Iterative Sliding and Increment Feedback[J]. Control and Design,2011,26(2): 132-135,139.

[9] 刘富樯. 无人水下航行器执行机构故障诊断与容错控制研究[D]. 西安: 西北工业大学,2015.

[10] Arslan M S,Fukushima N,Hagiwara I. Nonlinear Optimal Control of an AUV and its Actuator Failure Compensation[C]//10th International Conference on Control,Automation,Robotics and Vision,ICARCV 2008,Hanoi,Vietnam: IEEE,2008.

[11] Podder T K,Antonelli G,Sarkar N. Fault Tolerant Control of an Autonomous Underwater Vehicle under Thruster Redundancy: Simulations and Experiments[C]//IEEE International Conference on Robotics and Automation. San Francisco,USA: IEEE,2000.

[12] Cristofaro A,Johansen T A. Fault Tolerant Control Allocation Using Unknown Input Observers[J]. Automatica,2014,50(7): 1891-1897.

[13] Dos Santos C H F,Cardozo D I K,Reginatto R,et al. Bank of Controllers and Virtual Thrusters for Fault-tolerant Control of Autonomous Underwater Vehicles[J]. Ocean Engineering,2016,121: 210-223.

[14] Sarkar N,Podder T K,Antonelli G. Fault-accommodating Thruster Force Allocation of an AUV Considering Thruster Redundancy and Saturation[J]. IEEE Transactions on Robotics & Automation,2002,18(2): 223-233.

[15] Soylu S,Buckham B J,Podhorodeski R P. A Chattering-free Sliding-mode Controller for Underwater Vehicles with Fault-tolerant Infinity-norm Thrust Allocation[J]. Ocean Engineering,2008,35(16): 1647-1659.

[16] Fossen T I. Marine Control Systems: Guidance,Navigation and Control of Ships[M]. Norway: Marine Cybernetics,2002.

[17] Rauber J G,Santos C H F D,Chiella A C B,et al. A Strategy for Thruster Fault-tolerant Control Applied to an AUV[C]//17th International Conference on Methods & Models in Automation & Robotics. Miedzyzdroje,Poland: IEEE,2012.

[18] 高剑,徐德民,严卫生,等. 基于自适应反演滑模控制的AUV水平面动力定位方法[J]. 机械科学与技术,2007,26(6): 738-740.

Gao Jian,Xu De-min,Yan Wei-sheng,et al. Backstepping Sliding Mode Control of Dynamic Positioning of an Autonomous Underwater Vehicle(AUV)[J]. Mechanical Science and Technology for Aerospace Engineering,2007,26(6): 738-740.

[19] Buckholtz K R. Approach Angle-based Switching Function for Sliding Mode Control Design[C]//Proceedings of the 2002 American Control Conference. Anchorage,USA: IEEE,2002.

[20] 金鸿章,罗延明,肖真,等. 抑制滑模抖振的新型饱和函数法研究[J]. 哈尔滨工程大学学报,2007,28(3): 288-291.

Jin Hong-zhang,Luo Yan-ming,Xiao Zhen,et al. Investigation of a Novel Method of Saturation Function for Chattering Reduction of Sliding Mode Control[J]. Journal of Harbin Engineering University,2007,28(3): 288-291.

[21] Capisani L M,Ferrara A,Ferreira de Loza,A,et al. Manipulator Fault Diagnosis via Higher Order Sliding-Mode Observers[J]. IEEE Transactions on Industrial Electronics,2012,59(10): 3979-3986.

[22] Mahmoud Magdi S,Xia Y. Analysis and Synthesis of Fault-Tolerant Control Systems (Mahmoud/Analysis)|| Industrial Fault-Tolerant Architectures[M]//Analysis and Synthesis of Fault-Tolerant Control Systems. USA: John Wiley & Sons,Ltd,2014: 175-218.

[23] Omerdic E,Roberts G. Thruster Fault Diagnosis and Accommodation for Open-frame Underwater Vehicles[J]. Control Engineering Practice,2004,12(12): 1575-1598.

[24] 刘富樯,徐德民,高剑,等. 水下航行器执行机构的故障诊断与容错控制[J]. 控制理论与应用,2014,31(9): 1143-1150.

Liu Fu-qiang,Xu De-min,Gao Jian,et al. Fault Diagnosis and Fault Tolerant Control for Actuators of Underwater Vehicles[J]. Control Theory＆Applications,2014,31(9): 1143-1150.

Fault-tolerant Control of AUV Thruster Based on Adaptive Backstepping Sliding Mode

,

(State Key Laboratory of Ocean Engineering,Shanghai Jiaotong University,Shanghai 200240,China)

To achieve the robustness requirements of an autonomous undersea vehicle(AUV) for motion control in the case of thruster failure,this study designs an adaptive backstepping sliding mode motion tracking controller for the six-degree-of-freedom nonlinear vector motion model of the AUV and uses it in the thrust allocation. In the thrust distribution,the fault characteristics of the thruster are considered,and a continuous time-varying fault model is established. The fault adjustment function is added by incorporating the fault information,through the pseudo-inverse technique,based on the configuration of the structure function of the adjustment controller. The control input can be changed to correct the fault,and the fault adjustment and control reconstruction are adopted for different types of faults. This method realizes a fault-tolerant control under the fault state of the thruster and effectively improves the application universality of the fault-tolerant control algorithm. A variety of failure modes are simulated to verify the effectiveness of the adaptive fault-tolerant controller for AUV motion control in the case of thruster failure

autonomous undersea vehicle; thruster; adaptive control; fault adjustment; fault-tolerant control

U674.941; TP302.8

A

2096-3920(2021)04-0420-08

10.11993/j.issn.2096-3920.2021.04.008

张瀚文,王俊雄. 基于自适应反步滑模的AUV推进器容错控制[J]. 水下无人系统学报,2021,29(4): 420-427.

2020-10-26;

2020-12-02.

张瀚文(1996-),男,在读硕士,主要研究方向为水下机器人自动控制技术.

(责任编辑: 许 妍)