波浪滑翔器柔性水翼推进性能数值仿真分析

刘 芬,彭 彬,孙秀军,桑宏强,2

波浪滑翔器柔性水翼推进性能数值仿真分析

刘 芬1,彭 彬1,孙秀军3,4*,桑宏强1,2

(1.天津工业大学机械工程学院,天津,300387; 2.天津市现代机电装备技术重点实验室,天津,300387; 3.中国海洋大学物理海洋教育部重点实验室,山东 青岛,266100; 4.青岛海洋科学与技术试点国家实验室,山东 青岛,266237)

水翼是波浪滑翔器波浪动力转换的关键部件,直接决定了波浪滑翔器的航行性能。文中研究了波浪滑翔器柔性水翼的推进性能,根据波浪滑翔器工作时水翼的运动特点,基于COMSOL Multiphysics软件仿真出柔性水翼主动升沉运动下被动变形的过程,重点研究波浪参数、俯仰运动参数和斯特哈劳尔数对推进性能的影响。仿真结果表明,在一定范围内,水翼推进性能随波高、斯特哈劳尔数的增大而增大,随波周期的增大而减小; 当波周期较大时,波高和波周期的变化对水翼推进性能的影响较小; 当俯仰周期与波周期相等时,俯仰运动对水翼推进性能有积极作用。文中结果可为波浪滑翔器被动柔性水翼后续研究提供参考。

波浪滑翔器; 柔性水翼; 推进性能; 数值仿真

0 引言

波浪滑翔器是一种新型海洋移动观测平台,可以将波浪能转换为前向驱动动能,具有长期自主观测能力,目前已广泛应用于水文气象数据观测、环境监测、生物追踪及远程预警等领域[1-3]。

水翼作为决定波浪滑翔器波浪动力转换的关键部件,国内外学者已经进行了大量研究。桑宏强等[4]通过仿真分析提出了振荡水翼的最优运动方法,研究了水翼运动的极限位置等对波浪滑翔器推进速度的影响; 吕博元等[5]应用STAR-CCM+软件对水翼的摆动进行仿真,研究了被动摆动、主动摆动、限位角及波浪参数等对水翼推进性能的影响,可知主动摆动的推进性能优于被动摆动,水翼推进性能受波浪参数影响较大,且随波高和波浪频率的增加而增加,在波浪频率较小时,波浪频率的变化对推进性能的影响较小; Liu等[6]对规则波作用下振荡柔性水翼的推进性能进行了研究,可知在规则波波动频率与水翼振荡频率相等的情况下,水翼的推进性能最佳; Liu等[7]针对后缘柔性的主动振荡水翼能量汲取性能进行研究,发现水翼柔性激励了前缘涡的产生,提升了能量汲取能力; Alben等[8]发现自主推进柔性体的推进速度存在共振峰值,提出理论模型,并通过了实验验证; Prempraneerach等[9]进行了二维柔性摆动水翼实验,发现合理的弦向变形使得水翼效率提高了36%; Katz等[10]通过势流理论分析得出,当柔性尾鳍具有弦向变形时,其推进效率比刚性尾鳍高; 田宝强等[11]在传统波浪滑翔器的基础上,引入了柔性蹼翼,搭建了原理样机,通过水池实验验证了结构的可行性; 周凯[12]研究了典型仿生水翼的推进及能量吸收机制,结果表明对称运动模式下水翼的推进性能随斯特哈劳尔数的增大而增大,斯特哈劳尔数过大,会导致流场的不稳定。

文中在传统波浪滑翔器的基础上,引入柔性水翼进行研究,以期进一步提升波浪滑翔器的航行性能。根据波浪滑翔器及其水翼机构特殊的运动方式与特点,利用COMSOL Multiphysics软件中的流体模块、多体动力学模块和多物理场耦合模块,仿真柔性水翼随波浪滑翔器运动过程中产生的升沉运动、俯仰运动及形变的耦合过程。研究运动参数对柔性水翼推进性能的影响,主要包括波浪参数、俯仰运动参数以及斯特哈劳数,可为柔性水翼的开发提供参考。

1 柔性水翼物理模型

1.1 工作原理

为进一步提升波浪滑翔器的航行性能,引入柔性水翼。柔性水翼在结构上与传统波浪滑翔器的水翼机构有很大的差别,其主要通过在水动力下的弹性变形实现波浪能的吸收与利用。柔性水翼的优点主要表现在: 较刚性水翼结构更简单,可靠性强; 较刚性水翼更易轻质,同等水动力条件下具有较小的惯性; 可综合利用波浪滑翔器的升沉、俯仰和横滚运动产生前向驱动力。

根据以往的实验可知,波浪滑翔器在实际运动中的横滚较小,一般不超过±5°,因此文中不考虑波浪滑翔器横滚运动对柔性水翼的影响。假定波浪滑翔器以恒定的速度前向运动,当波峰来临时,波浪滑翔器在波浪的作用下产生上升运动与俯仰运动,同时柔性水翼受水动力的作用沿中心线向下弯曲,与水流形成一定攻角,柔性水翼因此受到升力和阻力的共同作用而产生前向动力,进而作用于波浪滑翔器,如图1(a)所示; 当波谷来临时,波浪滑翔器在波浪的作用下产生下沉运动与俯仰运动,同时柔性水翼在水动力的作用下沿中心线向上弯曲,与水流形成一定的攻角,柔性水翼因此受到升力和阻力的共同作用产生前向运动,进而作用于波浪滑翔器,如图1(b)所示。因此,柔性水翼在波浪中始终通过前向驱动力完成对滑翔机的推进。

1.2 运动规律

实际海况中,波浪形式非常复杂,导致水翼在波浪中的运动也极为复杂,通过数值仿真极难实现。为方便后续研究,结合线性波理论与柔性水翼的工作原理,对运动过程进行简化,赋予柔性水翼升沉运动、俯仰运动以及流场作用下的变形,将波浪的运动、柔性水翼的升沉运动与俯仰运动均设定为正弦函数,具体表达式为

波浪滑翔器能够充分利用波浪的起伏将水动力转化为前向推力,在升沉方向具有良好的随波性,因此认为波浪运动与柔性水翼升沉运动变化一致; 柔性水翼由初始状态下沉时,在水动力的作用下,俯仰运动角由平衡位逐渐向负向增大; 翼前缘相对于波浪滑翔器是固定的,所以翼俯仰运动中心相对位置也是固定的,但为了后续研究的典型性,文中简化翼前缘与俯仰运动中心一致。根据上述表述,可将式(1)中的参数设定为

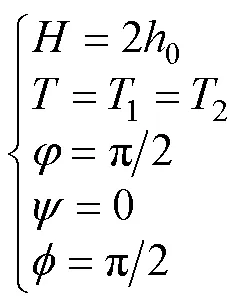
1.3 动力学参数

对于柔性水翼而言,无量纲参数斯特哈劳尔数对推进性能有很大的影响,且

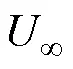
为更方便和直观地衡量柔性水翼推进性能,将其在流场中前向方向的受力转化为无量纲形式[5],推力系数为

为更直观地对比柔性水翼推进性能,计算得到1个周期内的平均推力系数[5]为

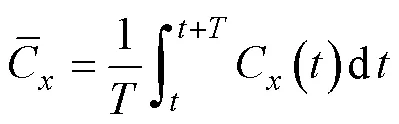
式中,为波周期。

2 仿真模型建立

2.1 计算模型

柔性水翼采用NACA0006翼型剖面,如图2所示。文中取翼弦长度为180 mm,翼后缘长度C为140 mm,翼前缘长度C为40 mm。

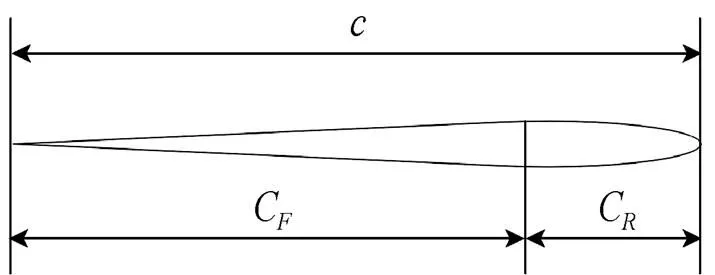
图2 柔性水翼模型

翼后缘呈弹性,其柔度系数E[12]定义为

式中: 取E为5.7×103;为翼后缘的杨氏模量。

2.2 计算域及网格划分

采用动网格技术研究柔性水翼在流场中的水动力特性。如图3所示,柔性水翼的计算域为20×(+20),翼表面设置为无滑移边界条件,其中心与计算域纵向中心线的距离为/2,与计算域横向中心线重合,右侧边界设置为速度入口,左侧边界设置为压力出口,上下边界设置为壁面。为确保计算的准确性,翼表面增设大小为5×5的变形域,其中心与翼中心重合,变形域顶点与整体计算域顶点连线作辅助边界。

采用湍流模型和COMSOL Multiphysics软件对计算域进行非结构网格划分,图4为网格划分示意图。

图3 计算域及边界条件示意图

图4 计算域网格划分

2.3 模型验证

为验证所建立模型的准确性,对网格尺寸以及计算可靠性进行验证。

2.3.1 网格无关验证

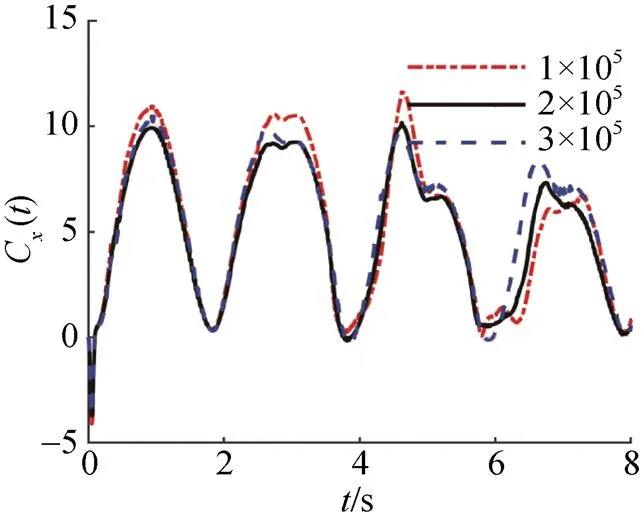
图5 不同网格数量下翼推力系数变化曲线

2.3.2 可靠性验证

表1 计算结果对比

3 仿真结果与分析

3.1 波浪参数对翼推进性能的影响

重点分析波高和波周期对翼推进性能的影响,其中波高为0.2～0.8 m,以0.2 m间隔选取,波周期为2～8 s,以2 s间隔选取,具体参数如表2所示。

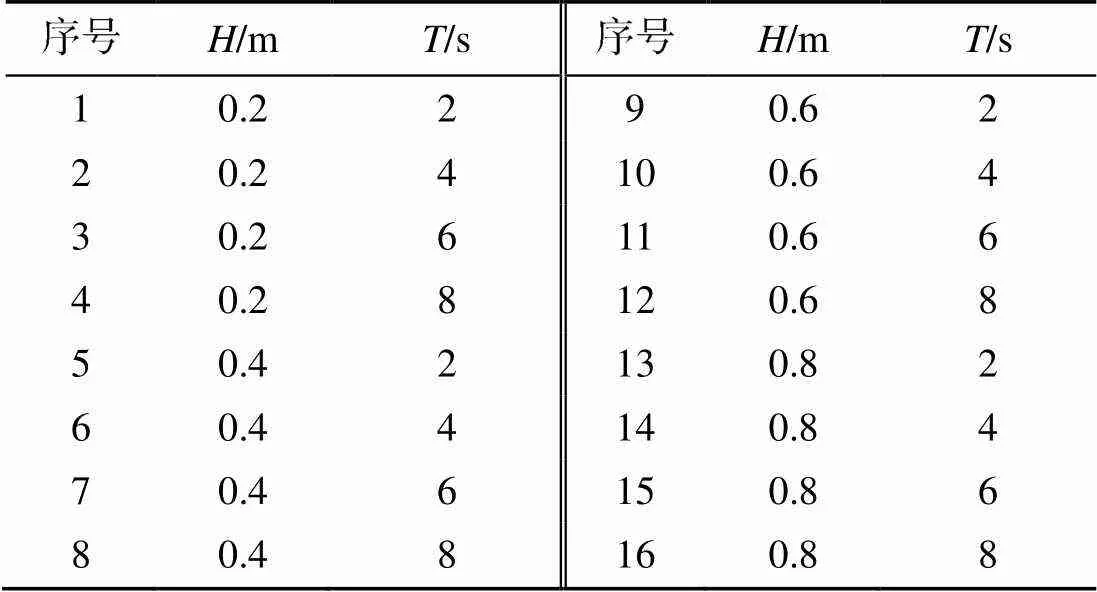
表2 数值仿真波浪参数

3.1.1 波高

图6是波周期分别为=2,4 ,6,8 s时,不同波高下翼推力系数C()随时间变化曲线。由于第1个周期处于启动阶段,流场处于不稳定状态,而第2个周期稳定程度相对较好,因此选择第2个周期进行分析。

由图6(a)可知,推力系数随波高的增大而增大,且在波高=0.4,0.6,0.8 m时,推力系数随时间的变化波动较大,没有呈现出明显的周期性,说明柔性水翼运动中周围的流场并未趋于稳定; 而在波高为0.2 m时,推力系数随时间的变化明显较小,且呈现出明显的周期性。由此可知,当波周期=2 s时,较小的波高可使流场和推力系数趋于稳定,较大的波高会导致流场与推力系数的不稳定。

由图6(b)～(d)可知,波周期=4,6,8 s时仍具有上述规律,且随着波周期的增大,流场和推力系数在更大波高下稳定变化,其中: 波周期=4 s、波高=0.4 m; 波周期=6 s、波高=0.8 m; 波周期=8 s、波高=0.8 m时,推力系数趋于稳定。

笔者相信，以村落民俗志为基础的乡村研究，在当今中国重述“亚洲”、重写“世界史”和“全球史”的学术热潮中，不仅没有过时，而且不可或缺。毕竟，体察中国国情，理解中国道路，提炼中国话语，仍要以“在村落里研究”[注][美]克利福德·格尔茨：《文化的解释》，韩莉译，译林出版社，1999年，第29页。 的乡土中国学术实践为立足点。

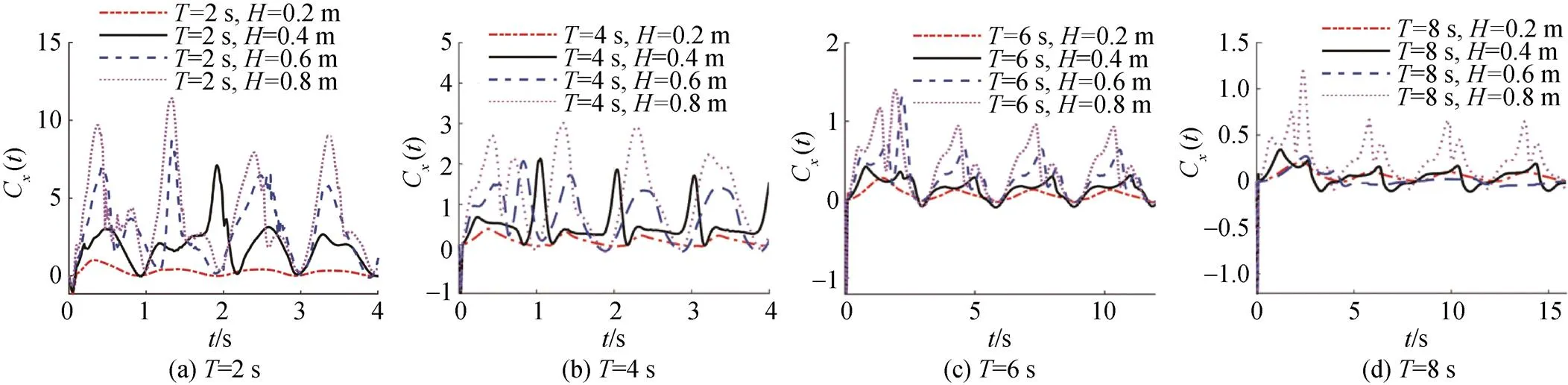
图6 不同波高下翼推力系数随时间变化曲线

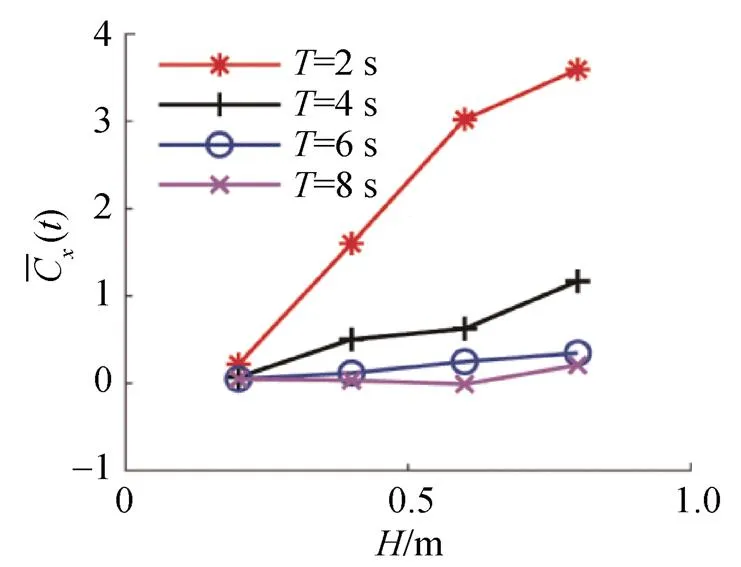
图7 不同波高下翼平均推力系数变化曲线

3.1.2 波周期

图8为翼推力系数在2个波周期随时间变化的曲线,波高为=0.2,0.4,0.6,0.8 m。基于上节所述原因,选择第2个周期进行分析。

由图8(a)可知,推力系数随波周期的增大而减小,且在波周期=4,6,8 s时,推力系数随时间变化波动较小,呈现出明显的周期性,流场趋于稳定,而在波周期=2 s时,推力系数随时间的变化波动较大,没有呈现出明显的周期性,流场并未趋于稳定。可见,当波高为0.2 m时,较大的波周期可使流场和推力系数趋于稳定,较小的波周期会导致流场与推力系数的不稳定。

由图8(b)～(d)可知,波高=0.4,0.6,0.8 m时仍具有上述规律,且随着波高的增大,流场和推力系数在更大的波周期下稳定变化,其中波高=0.4 m、波周期=4 s,波高=0.6 m、波周期=4 s,波高=0.8 m、波周期=6 s时,推力系数趋于稳定。

图9为不同波周期下柔性水翼平均推力系数的变化曲线。由图可知,不同波高下,平均推力系数均随波周期的增大而减小,且当波周期较小时,变化幅度较大,说明波周期对翼推进性能的影响程度较大; 波周期较大时,变化幅度较小,说明波周期的变化对翼推进性能的影响较小。该结果与文献[5]相近。

3.2 俯仰运动参数对翼推进性能的影响

为分析俯仰运动参数对柔性水翼推进性能的影响,重点分析俯仰角幅值0和俯仰运动周期2对推进性能的影响,其中俯仰角幅值为0～15°,以5°间隔选取,俯仰运动周期为0～4 s,以2 s的间隔选取,设计的具体工况如表3所示。

图8 不同波周期下翼推力系数变化曲线

图9 不同波周期下翼平均推力系数变化曲线

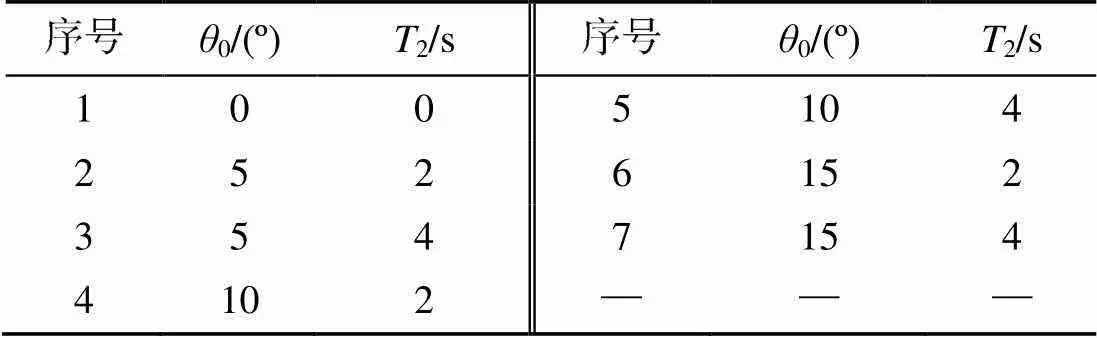
表3 数值仿真俯仰运动参数

3.2.1 俯仰角幅值

图10为柔性水翼推力系数在俯仰运动周期2=2,4 s时随时间变化的曲线,选择计算中的第2个周期进行分析。由图10(a)可知,在周期2=2 s时,随俯仰角幅值的增大,推力系数出现负值的区域逐渐增大,随时间变化的波动明显增大,没有呈现出明显的周期性,流场并未趋于稳定; 由图10(b)可知,在周期2=4 s时,随俯仰角幅值的增大,推力系数呈现良好的周期性,流场均趋于稳定。

图10 不同俯仰角幅值下翼推力系数变化曲线

图11 不同俯仰角幅值下翼平均推力系数变化曲线

图11中,当俯仰运动周期2与波周期相等时,俯仰角幅值在一定范围内增大,平均推力系数随之增大,变化幅度较小; 在俯仰运动周期为波周期的1/2时,平均推力系数随俯仰角幅值的增大而减小,变化幅度较大。可见,当俯仰运动周期与波周期相等时,在一定范围内,俯仰角幅值越大,推进性能越佳; 当俯仰运动周期为波周期的1/2时,在一定范围内,俯仰角幅值越小,推进性能越佳。

3.2.2 俯仰运动周期

图12为柔性水翼推力系数在2个波周期随时间变化的曲线,俯仰角幅值0=5°,10°,15°时,选择分析第2个周期。由图可知,俯仰运动周期的减小使得推力系数随着时间变化的波动明显增大,且周期性明显变差,流场由较稳定向较不稳定转变。

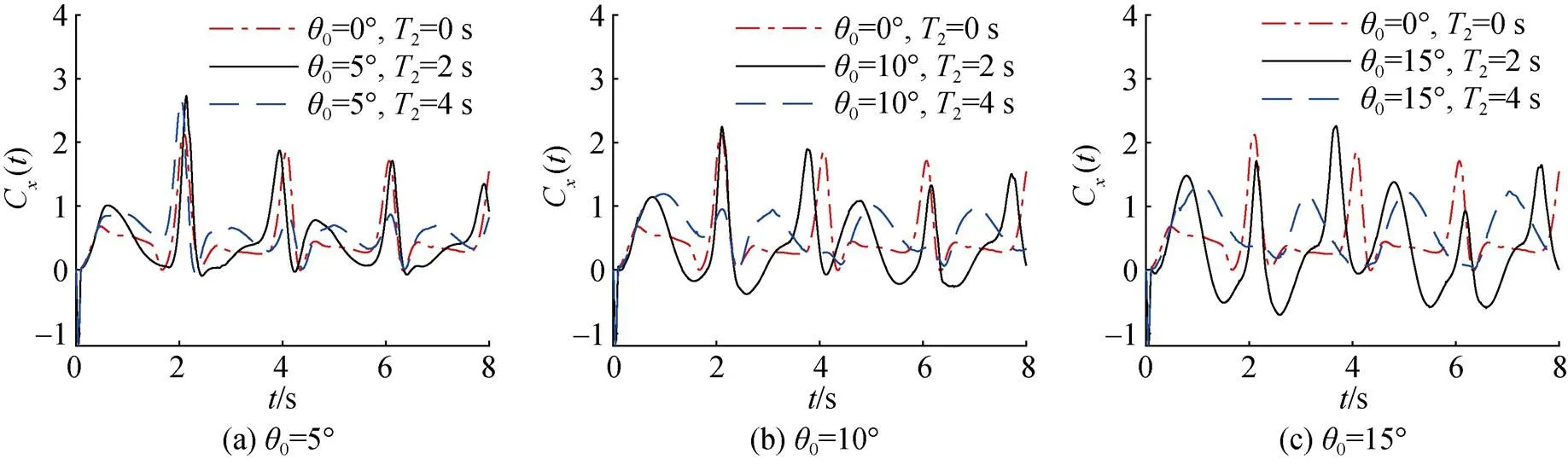
图12 不同俯仰运动周期下翼推力系数变化曲线

图13为不同俯仰运动周期下柔性水翼的平均推力系数变化曲线,由图可知,平均推力系数均随俯仰运动周期的增大呈先减小后增大的趋势,且在俯仰角幅值较小时,俯仰运动周期对平均推力系数的影响较小。

图13 不同俯仰运动周期下翼平均推力系数变化曲线

3.3 斯特哈劳尔数对翼推进性能的影响

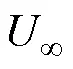
图14为柔性水翼推力系数在2个波周期内随时间变化曲线,斯特哈劳尔数=0.450,0.225,0.150,0.1125,0.090,选择计算中的第2个周期进行分析。

表4 数值仿真斯特哈劳尔数

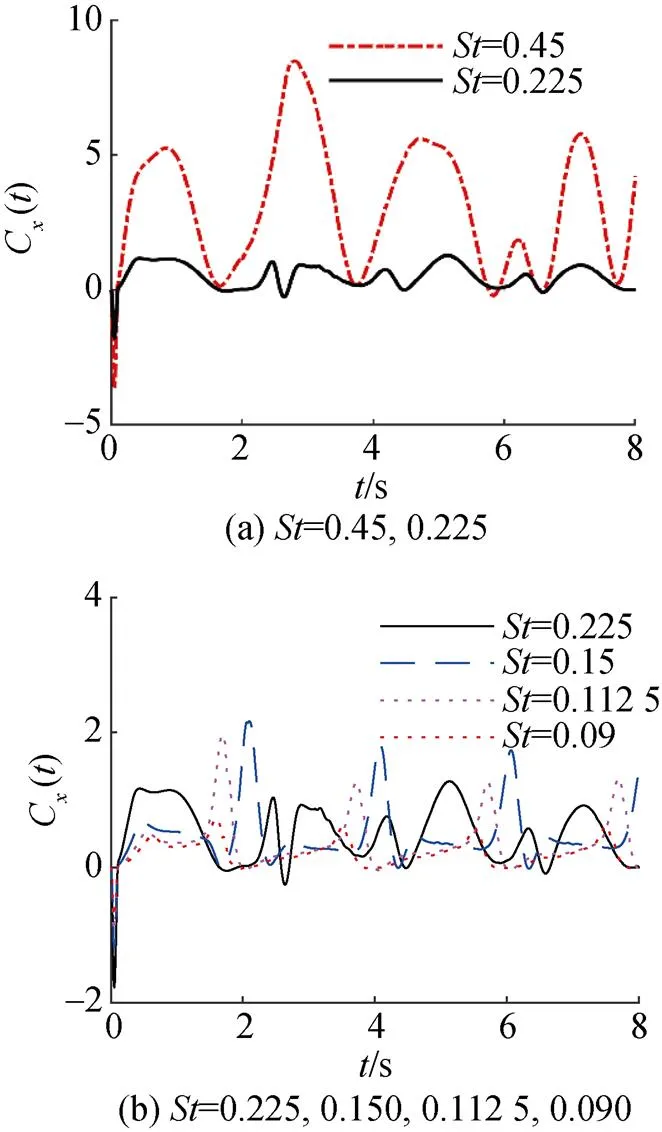
图14 不同斯特哈劳尔数下翼推力系数变化曲线

由图可知,随着斯特哈劳尔数的减小,推力系数随时间变化的波动明显减小,流场逐渐趋于稳定,呈现出明显的周期性,且当斯特哈劳尔数较小时,对推力系数的影响较小。

图15为不同斯特哈劳尔数下柔性水翼的平均推力系数变化曲线,由图可知,平均推力系数基本符合随斯特哈劳尔数增大而增大,斯特哈劳尔数较小时,其改变对平均推力系数的影响较小,该结果与文献[12]研究结果相近。

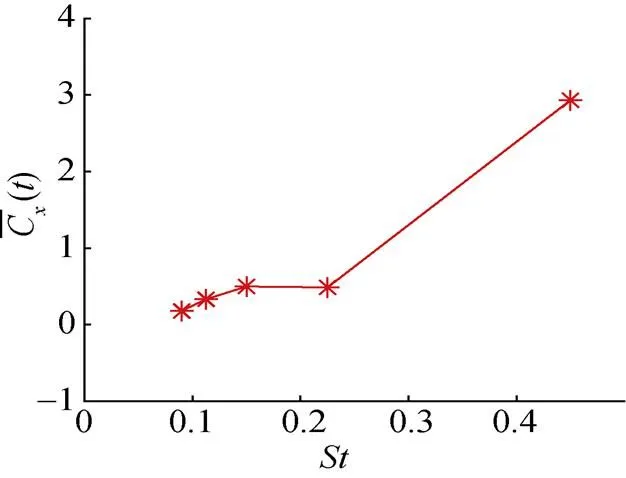
图15 不同斯特哈劳尔数下翼平均推力系数变化曲线

4 水池实验验证

4.1 实验平台搭建

水翼推进实验平台能够实现柔性水翼的升沉振荡运动,使得柔性水翼在流场作用下产生形变,从而产生前向推力。实验平台主要由气动装置、主体框架、滑动导轨、拉力测试仪和柔性水翼机构组成,通过调节气动装置的气压来调节柔性水翼升沉运动的行程和周期,主体框架搭载气动装置和柔性水翼机构,在与柔性水翼前向相反的方向安装拉力测试仪,实时接收柔性水翼机构的前向推力数据,实验平台如图16所示。

图16 实验平台

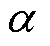
图17 柔性水翼几何参数

图18 柔性水翼实物图

4.2 实验结果分析

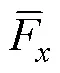
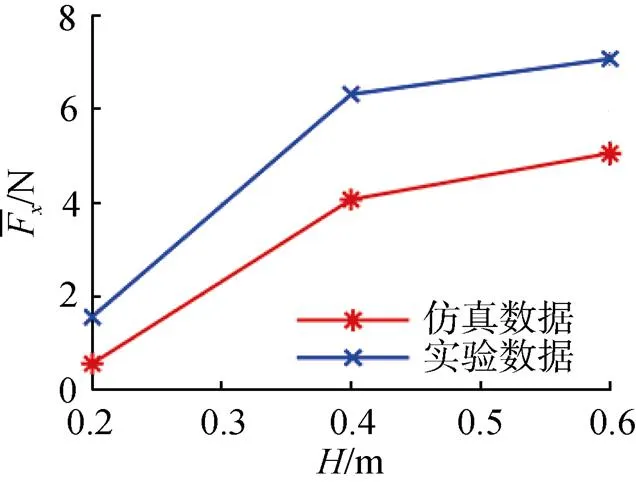
图19 波周期T=4 s下仿真与实验平均推力对比曲线

尽管存在一定偏差,但仿真数据与实验数据趋势性一致,符合前文仿真分析得出的规律,水池实验在一定程度上验证了文中的仿真结果。

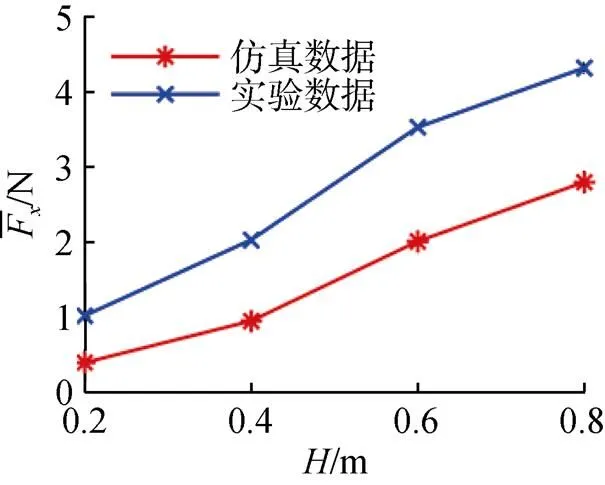
图20 波周期T=6 s下仿真与实验平均推力对比曲线

5 结论

文中以波浪滑翔器中的柔性水翼为研究对象,对柔性水翼在波浪中的运动进行仿真分析,重点分析了运动参数对翼推进性能的影响,得到如下结论: 1) 通过COMSOL Multiphysics软件的流体场与固体场相结合的模型,实现了柔性水翼在升沉运动和俯仰运动耦合中产生被动变形的仿真; 2) 在一定范围内,翼推进性能随波高的增大而增大,且较大的波高易导致翼周围的流场不稳定,当波周期较大时,波高对翼推进性能的影响较小; 3) 在一定范围内,翼推进性能随波周期的增大而减小,较小的波周期易导致翼周围流场不稳定,对翼推进性能的影响较大; 4) 在一定范围内,当俯仰运动周期与波周期相等时,俯仰运动对翼推进性能有积极作用,且俯仰角幅值越大,翼推进性能越佳,当俯仰运动周期与波周期不相等时,俯仰运动对翼推进性能有消极作用,且俯仰角幅值越小,翼推进性能越佳; 5) 在一定范围内,翼推进性能随斯特哈劳尔数的减小而减小,且在低斯特哈劳尔数下对翼推进性能影响较小; 6) 仿真数据和实验数据存在一定偏差,但二者趋势性相近,一定程度上验证了文中的仿真结果。

[1] Daniel T,Manley J,Trenaman N. The Wave Glider: Enabling a New Approach to Persistent Ocean Observation and Research[J]. Ocean Dynamics,2011,61(10): 1509-1520.

[2] Hine R,Willcox S,Hine G,et al. The Wave Glider: A Wave-Powered Autonomous Marine Vehicle[C]//Procee- dings of MTS/IEEE Biloxi-Marine Technology for Our Future: Global and Local Challenges. Biloxi,USA: IEEE,2009: 296-301.

[3] 廖煜雷,李晔,刘涛,等. 波浪滑翔器技术的回顾与展望[J]. 哈尔滨工程大学学报,2016,37(9): 1227-1236.

Liao Yu-lei,Li Ye,Liu Tao,et al. Unmanned Wave Glider Technology: State of Art and Perspective[J]. Journal of Harbin Engineering University,2016,37(9): 1227-1236.

[4] 桑宏强,李灿,孙秀军. 波浪滑翔器纵向速度与波浪参数定量分析[J]. 水下无人系统学报,2018,26(1): 16-22.

Sang Hong-qiang,Li Can,Sun Xiu-jun. Quantitative Analysis on Longitudinal Velocity and Wave Parameter of Wave Glider[J]. Journal of Unmanned Undersea Systems,2018,26(1): 16-22.

[5] 吕元博,田新亮,李欣,等. NACA 0012摆动扑翼水动力特性的二维数值模拟[J]. 中国舰船研究,2018,13(2): 7-15.

Lü Yuan-bo,Tian Xin-liang,Li Xin,et al. Two-dimen- sional Numerical Simulation of NACA 0012 Flapping Foil Hydrodynamics[J]. Chinese Journal of Ship Research,2018,13(2): 7-15.

[6] Liu P,Liu Y B,Huang S L,et al. Effects of Regular Waves on Propulsion Performance of Flexible Flapping Foil[J]. Applied Sciences,2018,8(6): 934.

[7] Liu W,Xiao Q,Zhu Q. Passive Flexibility Effect on Oscillating Foil Energy Harvester[J]. AIAA Journal,2016,54(4): 1-16.

[8] Alben S,Witt C,Baker T V,et al. Dynamics of Freely Swimming Flexible Foils[J]. Physics of Fluids,2012,24(5): 109-133.

[9] Prempraneerach P,Hober F S,Triantfyllou M S. The Effect of Chordwise Flexibility on the Trust and Efficiency of a Flapping foil[C]//Proceedings of the 13th International Symposium on Unmanned Untethered Submersible Technology. Durham,USA: IEEE,2003: 130-128.

[10] Katz J,Weihs D. Hydrodynamic Propulsion by Large Amplitude Oscillation of an Airfoil with Chordwise Flexibility[J]. Journal of Fluid Mechanics,1978,88(3): 485-497.

[11] 田宝强,李玲珑. 蹼翼型波浪滑翔机结构设计和运动原理分析[J]. 中国机械工程,2017,28(24): 2939-2943.

Tian Bao-qiang,Li Ling-long. Structure Design and Movement Principle of Wave Gliders with Webbed Wings[J]. China Mechanical Engineering,2017,28(24): 2939-2943.

[12] 周凯. 典型仿生水翼的推进及能量吸收机制研究[D]. 哈尔滨: 哈尔滨工程大学,2018.

[13] Kinsey T,Dumas G. Computational Fluid Dynamics Analysis of a Hydrokinetic Turbine Based on Oscillating Hydrofoils[J]. Journal of Fluids Engineering,2012,134(2): 021104.

Numerical Simulation Analysis of Flexible Hydrofoil Propulsion Performance for Wave Glider

1,1,3,4*,1,2

(1. School of Mechanical Engineering,Tianjin Polytechnic University,Tianjin 300387,China; 2.Tianjin Key Laboratory of Advanced Mechatronic Equipment Technology,Tianjin 30087,China; 3. Physical Oceanorgraphy Laboratory,Ocean University of China,Qingdao 266100,China; 4. Laboratory of Marine Dynamics and Climate Function,Pilot National Laboratory for Marine Science and Technology(Qingdao),Qingdao 266237,China)

The hydrofoil is a key component that determines the capability of wave power conversions and the navigation performance of wave gliders. The propulsion performance of a flexible hydrofoil is investigated in this study. The passive deformation process of a flexible hydrofoil under active heave motion is simulated using the COMSOL Multiphysics software according to the motion characteristics of a hydrofoil when the wave glider is working. The effects of wave and pitching motion parameters and the Strouhal number on the propulsion performance of the hydrofoil are investigated. The simulation results show that the propulsion performance of the hydrofoil increases with wave height and Strouhal number and decreases with wave period within a certain range. When the wave period is high,the change in wave height and wave period has little effect on the propulsion performance of the hydrofoil. In contrast,when the pitch and wave periods are equal,the pitching motion has a positive effect on the performance.

wave glider; flexible hydrofoil; propulsion performance; numerical simulation

TJ630; U674.941; O353

A

2096-3920(2021)04-0374-09

10.11993/j.issn.2096-3920.2021.04.002

刘芬,彭彬,孙秀军,等. 波浪滑翔器柔性水翼推进性能数值仿真分析[J]. 水下无人系统学报,2021,29(4): 374-382.

2020-08-28;

2020-11-11.

山东省重大科技创新项目(2019JZZY020701);天津市自然科学基金重点基金(18JCZDJC40100); 国家重点研发计划重点专项(2017YFC0305902); 青岛海洋科学与技术国家实验室“问海计划”项目(2017WHZZB0101).

通信作者简介:孙秀军(1981-),男,博士,教授,主要研究方向为波浪滑翔器技术及其海洋观测应用.

(责任编辑: 杨力军)