基于四元数反馈的UVMS滑模控制器设计

杜晓玮,侯冬冬,王红都,3,黎 明,3

基于四元数反馈的UVMS滑模控制器设计

杜晓玮1,侯冬冬2,王红都1,3,黎 明1,3

(1.中国海洋大学工程学院,山东 青岛,266100; 2.河南省水下智能装备重点实验室,河南 郑州,450015; 3.山东省海洋智能装备技术工程研究中心,山东 青岛,266100)

随着水下机器人-机械手系统(UVMS)向轻量化、敏捷化方向发展,对高精度水下姿态控制的需求日益突出。传统方法多使用欧拉角表示姿态,其在特殊姿态下求运动学逆解会产生奇异,不能满足特殊姿态作业的要求。因此,文中采用四元数表示水下机器人本体姿态,建立基于四元数的运动学模型,避免了欧拉角的万向锁问题。同时,进一步构建了UVMS的动力学模型,构造基于四元数误差的滑模面,设计了位置、姿态滑模控制器,并通过广义Lyapunov理论分析了系统的稳定性。为了实现更好的控制效果,利用时间误差绝对值函数设计适应度函数,采用遗传算法优化了控制器参数。仿真结果验证了控制器的有效性。

水下机器人-机械手系统; 四元数反馈; 滑模控制; 遗传算法; 参数优化

0 引言

为了开发海洋资源,开展水下作业任务,人们对水下机器人-机械手系统(undersea vehicle manipulator system,UVMS)进行了大量研究,取得了许多成果。在上世纪90年代,UVMS本体的体型和质量都比较大,如ALIVE[1]和SAUVIM[2]的机械手的运动就对本体影响较小。21世纪初期,对基于轻型自主水下航行器(autonomous undersea vehicle,AUV)本体的UVMS研究逐渐增多。GIRONA 500[3]是西班牙资助项目中开发的一种更轻便、更灵活的水下机器人,目前主要用于浅水作业,已经在许多项目中使用,如RAUVI、TRITON、TRIDENT、PANDORA和MERBOTS等项目[4]。

随着自主水下航行器(autonomous undersea vehicle,AUV)轻型化的发展,UVMS本体和机械手的质量比变小,导致系统的耦合性增强,控制难度增加,因此需要使用更先进的控制算法。Antonelli[5]详细讨论了UVMS的多种控制策略,如反馈线性化、前馈解耦控制、自适应控制、非线性控制、基于虚拟分解的控制等,并且分别在惯性坐标系和体坐标系下设计了多种控制方案。Dai等[6]提出了一种间接自适应控制方案,该方案由基于扩展卡尔曼滤波(extended Kalman filter,EKF)的补偿系统、基于模型计算转矩的控制器(a model-based computed torque controller,CTC)和鲁棒补偿跟踪控制器三部分组成,该控制器具有良好的干扰抑制效果。Dai等[7-8]又进一步研究了基于快速模型预测控制(fast model predictive control,FTMPC)的方法。Ramezani等[9]讨论了UVMS的自适应滑模控制,充分发挥了滑模控制抗参数变化和外部干扰的能力。Dai等[10]提出将滑模阻抗控制(sliding mode impedance control,SMIC)方法应用于I-AUV(UVMS的一种)的位置/力控制中,以完成某些水下操作任务。

用欧拉角表示姿态具有直观、易于理解等优点,因此在上述文献中,大多采用欧拉角来表示本体的姿态,设计反馈进行控制,但是在俯仰角接近90°时,欧拉角方法无法处理,逆运动学求解会出现多解问题,产生姿态表示上的奇异。为了满足一些特殊的操作任务或减少上升过程中的阻力,UVMS本体的姿态需要更加多样化,同时水下航行器的小型化和轻量化也使得这种姿态成为可能,此时使用欧拉角表示姿态,便会产生奇异。而使用四元数表示本体的姿态可以很好地解决此类问题。

Fjellstad等[11]详细介绍了如何使用四元数表示UVMS本体的姿态,建立了对应的运动学模型,并设计了比例-积分-微分(proportional integral derivative,PID)控制器进行了控制仿真。Antonelli 等[12-13]基于四元数反馈设计了一种滑模控制器,而后又进一步设计了自适应参数的控制器,并且在AUV的全方位智能导航器(omni-directional intelligent navigator,ODIN)上进行了实验验证。Arrichiello等[14]基于四元数反馈,研究了安装单方向驱动器的AUV的位置和姿态控制,其控制策略基于有界单纯形法。

滑模控制器对克服干扰和系统的不确定性有很强的鲁棒性,尤其是对非线性系统具有良好的控制效果,且算法简单,响应速度快。而结合滑模控制与四元数反馈对UVMS进行控制的文献比较少。因此,为了避免欧拉角的万向锁问题,建立了基于四元数的运动学模型。针对UVMS这一强耦合、非线性的复杂系统,设计了基于四元数误差的滑模控制器,对UVMS的姿态进行控制,分析了控制器的稳定性。为了得到更优的控制器参数,利用时间误差绝对值函数(integ- rated time absolute error,ITAE)设计适应度函数,将控制器参数选择问题转化成遗传算法(genetic algorithm,GA)的优化问题。仿真结果表明了控制器的有效性。

1 基于四元数的UVMS建模

1.1 正运动学模型

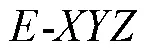
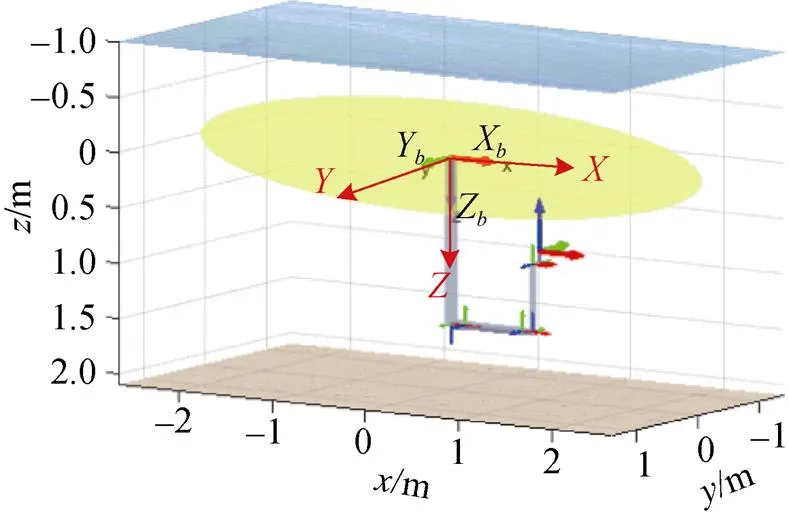
图1 UVMS坐标系示意图

基于四元数的表示方法,本体速度在体坐标系与惯性坐标系之间的变换关系如下[12]

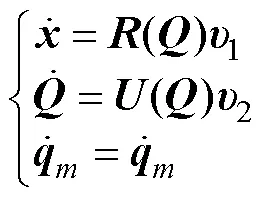
其中

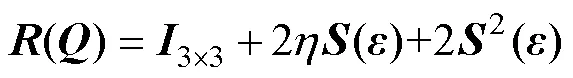
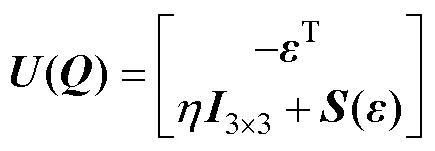
机械臂从肩部关节到末端手爪关节依次编号1～6,仿真模型是Smart3S机械臂[5],使用标准DH法建模后得到的DH参数如表1所示。

根据标准DH法对应的坐标系变换矩阵,可以利用本体位置、DH参数表和机械臂各关节角度计算末端手爪的位置。

1.2 逆运动学模型

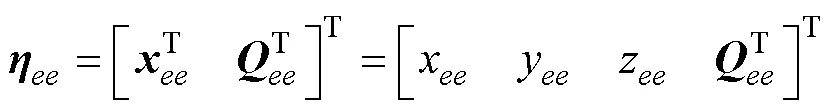
表1 机械臂DH参数表

可以通过简化的方式计算体坐标系下的参考速度[5](下标表示期望值),即

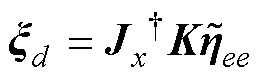
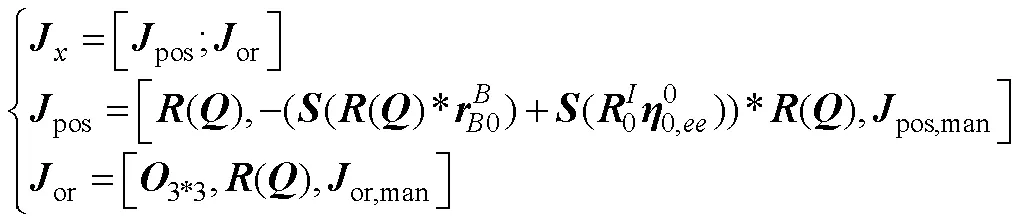
1.3 动力学模型

结合Fossen经典六自由度动力学模型[15-17],并根据机械臂的自由度进行扩展,最终得到十二自由度的UVMS动力学模型[5]

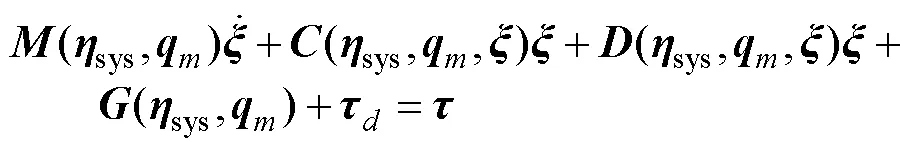
动力学模型满足以下3个重要的性质[12],将模型中的质量惯性矩阵、科氏力和向心力矩阵、阻尼系数矩阵简化为、、,得

2 滑模控制器设计

2.1 滑模面及误差定义

姿态误差的时间导数为

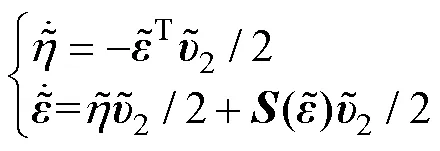
滑模面是速度误差和位姿、关节角度误差的线性组合

2.2 控制器设计

文中设计的滑模控制器为

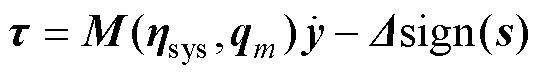
2.3 稳定性证明

针对式(13),选用如下李雅普诺夫函数分析系统的稳定性

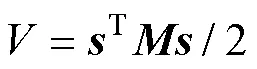
其导数为

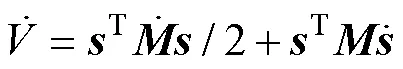
将滑模面式(13)的导数形式和动力学模型性质式(9)代入式(17),得到

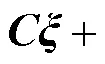
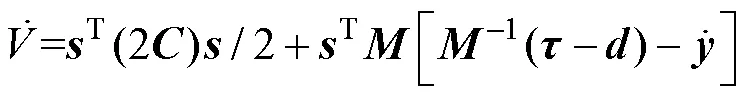
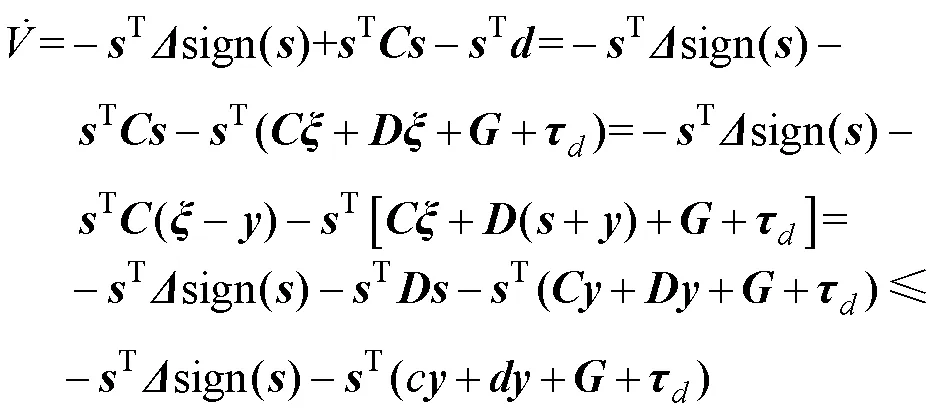
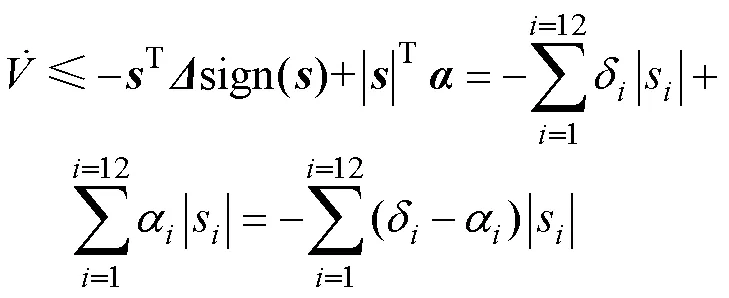
3 基于GA的控制器参数优化

式中:是仿真总时长;()是时刻的误差。式(22)是连续函数的积分形式,不便于仿真计算,需对其作离散化处理,得到离散条件下的ITAE,即

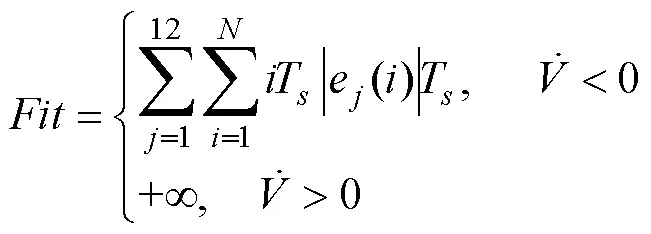
终止条件为多个条件的并集,包括期望的适应度值、最大的迭代次数、优化停滞不前的次数,满足其中任何一个条件,即可结束当前的优化过程。参数优化流程图如图2所示。

图2 基于遗传算法的参数优化流程图

4 仿真试验与结果分析

整个控制系统仿真框图如图3所示。设计了滑模控制器并优化了参数,最终实现了末端手爪的定点控制。

图3 系统仿真框图

文中使用的UVMS模型参数可以参考文献[5]。使用的开源函数库Simurv4.0也可以参考文献[5]。Simurv4.0不是一个一键式的模拟器,而是一个通用函数库,包含常用的坐标转换矩阵和雅可比矩阵等,可以用它来测试UVMS的运动学和动力学控制算法。

为了减少滑模控制器的抖振,仿真过程中使用饱和函数代替符号函数式(15)

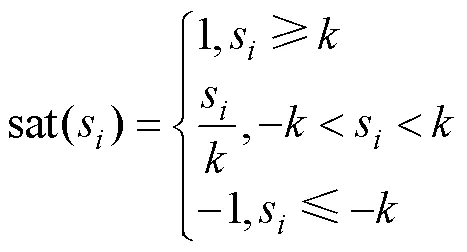
式中,是边界层,仿真中=2。

控制器更新为

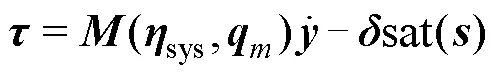
仿真分为2个阶段进行: 第1阶段,进行定点控制,将本体姿态的俯仰角设定为90°,验证四元数姿态表示的无奇异性,同时利用MATLAB的GA工具箱对滑模控制器参数进行优化,控制目标是使UVMS机械臂的末端手爪接近目标点; 第2阶段,加入轨迹规划和逆运动学求解,使机械臂末端手爪移动到指定位置,并通过运动学正向计算验证,最后绘制UVMS的状态图和各仿真曲线。控制器的仿真步长均为0.005 s,仿真总时长均为20 s。

阶段1: 首先对UVMS实现定点控制,本体的期望位置为[12 2 4]。后续没有特殊说明的情况下,位置坐标的单位都是m,即UVMS体坐标系的原点需要从惯性坐标系下的[0 0 0]点移动到 [12 2 4]点; 本体的期望姿态角为[0 90 0]°,俯仰角设定为90°,来验证四元数表示的无奇异性; 关节角的设定值为[0 -70 -30 -30 -170 -90]°,处于一种伸展的状态。

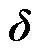
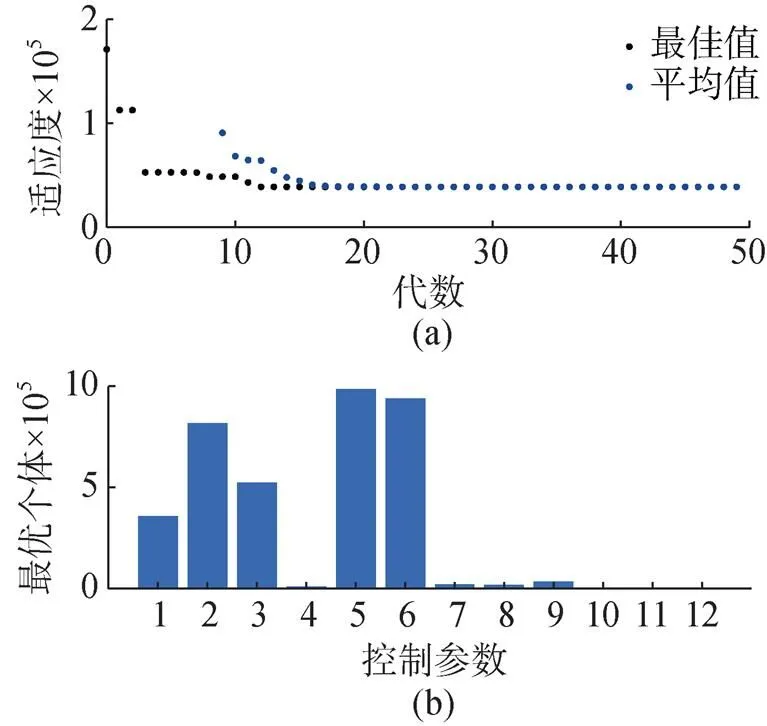
图4 GA优化结果图

将GA寻优得到的最佳个体,作为控制器的参数,绘制UVMS的仿真效果图。其中,UVMS的终止状态和运行轨迹如图5(a)所示,所绘制的轨迹是本体的重心轨迹; 刚体的位置和姿态跟踪性能如图5(b)所示,可知俯仰角最终达到88.8°,虽然存在1.2°的稳态误差,但并没有产生欧拉角表示的奇异问题; 刚体的位置误差如图5(c)所示; 机械臂关节角度的时间变化曲线如图5(d)所示。由图5可知,系统响应速度较快,基本在6 s左右即可达到稳定状态,且稳态误差较小,表明了控制器良好的控制效果。

阶段2: 在阶段1之后,UVMS机械臂的末端手爪已经到达目标点[3 3.5 14]附近。此时,使用梯形速度曲线规划末端手爪从当前位置到指定位置的轨迹,通过式(6)进行逆运动学求解,可得到体坐标系下的参考速度,进而通过坐标变换,转换到惯性坐标系下并进行积分,可得到惯性坐标系下的参考位置,即控制器的设定值。

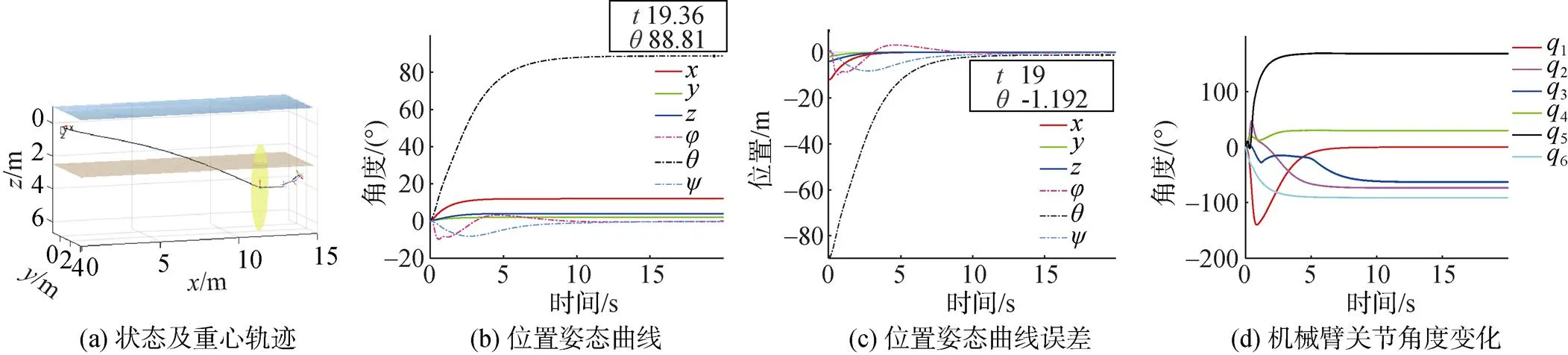
图5 阶段1仿真曲线

在仿真过程中,UVMS抓取前、后的状态分别如图6(a)～(b)所示。注意抓取的初始状态是阶段1的结束状态。机械臂末端手爪的实际位置和参考位置如图7所示,可知该控制器可以精确地到达目标位置,并且抖振较小,具有较好的控制效果。

图6 抓取前后状态图

图7 末端手爪实际与参考位置曲线

5 结束语

文中采用四元数反馈的方法为UVMS设计了滑模控制器,避免了俯仰角接近90°时,欧拉角进行姿态表示的多解问题,即避免了姿态表示的奇异性; 并在仿真中设计特殊的作业情况,验证四元数姿态表示的有效性。同时为了得到更好的控制效果,利用MATLAB的GA工具箱对控制器参数进行优化,设计适应度函数,取最小适应度值对应的种群个体作为控制器的参数。仿真试验验证了控制器的有效性。最后通过运动学逆解、坐标变换和积分,实现了机械臂末端手爪的定点控制。后续需要进一步研究存在障碍物的情况下,如何进行路径规划,以及进一步考虑末端手爪的姿态,而非仅实现末端手爪的位置控制。

[1] Evans J,Redmond P,Plakas C,et al. Autonomous Docking for Intervention-AUVs Using Sonar and Video-based real-time 3D Pose Estimation[C]//Oceans. San Diego,CA,USA: IEEE,2003.

[2] Marani G,Choi S K,Yuh J. Underwater Autonomous Manipulation for Intervention Missions AUVs[J]. Ocean Engineering,2009,36(1): 15-23.

[3] Ribas D,Palomeras N,Ridao P,et al. Girona 500 AUV: From Survey to Intervention[J]. IEEE/ASME Transactions on Mechatronics,2012,17(1): 46-53.

[4] Zereik,Bibuli E,Marco,et al. Challenges and Future Trends in Marine Robotics[J]. Annual Reviews in Control,2018,46: 350-368.

[5] Antonelli G. Underwater Robots[M]. Berlin Heidelberg: Springer,2014.

[6] Dai Y,Yu S. Design of an Indirect Adaptive Controller for the Trajectory Tracking of UVMS[J]. Ocean Engineering,2018,151: 234-245.

[7] Dai Y,Yu S,Yan,et al. An EKF-Based Fast Tube MPC Scheme for Moving Target Tracking of a Redundant Underwater Vehicle-Manipulator System[J]. IEEE/ASME Transactions on Mechatronics,2020,24(6): 2803-2814.

[8] Dai Y,Yu S,Yan Y. An Adaptive EKF-FMPC for the Trajectory Tracking of UVMS[J]. IEEE Journal of Oceanic Engineering,2019,45(3): 1-15.

[9] Ramezani-Al M R,Sereshki Z T. A Novel Adaptive Sliding Mode Controller Design for Tracking Problem of an AUV in the Horizontal Plane[J]. International Journal of Dynamics and Control,2019,7(2): 679-689.

[10] Dai P,Lu W,Le K,et al. Sliding Mode Impedance Control for Contact Intervention of an I-AUV: Simulation and Experimental Validation[J]. Ocean Engineering,2020,196: 106855.

[11] Fjellstad O E,Fossen T I. Position and Attitude Tracking of AUV’s: a Quaternion Feedback Approach[J]. IEEE Journal of Oceanic Engineering,2002,19(4): 512-518.

[12] Antonelli G,Chiaverini S. Singularity-free Regulation of Underwater Vehicle-manipulator Systems[C]//Proceedings of the 1998 American Control Conference. ACC(IEEE Cat. No.98CH36207). Philadelphia,USA: IEEE,1998,1: 399-403.

[13] Antonelli G,Chiaverini S,Sarkar N,et al. Adaptive Control of an Autonomous Underwater Vehicle: Experimental Results on ODIN[J]. IEEE Transactions on Control Systems Technology,2001,9(5): 756-765.

[14] Arrichiello V,Bartolini G,Pisano A,et al. Attitude and Position Tracking of Autonomous 6 DOF Vehicles with Mono-directional Actuators[C]//2016 14th International Workshop on Variable Structure Systems(VSS). Nanjing,China: IEEE,2016: 80-85.

[15] Thor I F. Guidance and Control of Ocean Vehicles[M]. Chichester,UK: John Wiley & Sons,1994.

[16] 魏延辉. UVMS系统控制技术[M]. 哈尔滨: 哈尔滨工程大学出版社,2017: 19-69.

[17] 李小岗,王红都,黎明. 自主水下航行器机械臂系统非线性PD控制器设计[J]. 水下无人系统学报,2020,28(1): 24-32.

Li Xiao-gang,Wang Hong-du,Li Ming. Nonlinear PD Controller Design for Autonomous Undersea Vehicle-Manipulator System[J]. Journal of Unmanned Undersea Systems,2020,28(1): 24-32.

1. 薛乃耀,刘鲲,王冬姣,等. 考虑模型误差的ROV抗饱和控制设计. 2021,29(3).

2. 黄博伦,杨启. 基于super-twisting二阶滑模算法的作业型ROV路径跟踪控制方法. 2021,29(1).

3. 施文煜,梁霄,曲星儒,等. 基于RBF积分滑模的无人艇集群协同路径跟踪控制. 2020,28(6).

4. 徐鹏程,曾庆军,陈尧伟,等. 基于导管螺旋桨负载的ROV推进器滑模控制. 2020,28(5).

5. 王香,张永林. 基于RBF神经网络的AUV路径跟踪分数阶滑模控制. 2020,28(3).

6. 霍宇彤,郭晨,于浩淼. 欠驱动AUV三维路径跟踪RBF神经网络积分滑模控制. 2020,28(2).

7. 姜晓奇,刘维亭,魏海峰,等. 基于全阶状态滑模观测器的混合永磁记忆电机磁链观测. 2020,28(2).

8. 李小岗,王红都,黎明. 自主水下航行器机械臂系统非线性PD控制器设计. 2020,28(1).

9. 李鑫,黄茹楠,丁宁. 输入受限的自主水下航行器自适应反演控制. 2019,27(6).

10. 张明明,刘维亭,魏海峰,等. 基于滑模观测器的PMSM单相霍尔位置传感器故障容错控制算法. 2019,27(6).

11. 桑宏强,于佩元,孙秀军. 基于航向补偿的水下滑翔机路径跟踪控制方法. 2019,27(5).

12. 林树锋,王冬姣,叶家玮,等. 基于蚁群算法的水下机器人机械臂工作路径优化. 2019,27(1).

13. 齐贝贝,严卫生,高剑. 基于偶极势场的移动回收站空间回坞导引算法. 2018,26(3).

14. 严浙平,李响,宋育武,等. 参数摄动下基于积分滑模的欠驱动UUV轨迹跟踪控制方法. 2018,26(3).

Sliding Mode Controller Design Based on Quaternion Feedback for UVMS

1,2,1,3,1,3

(1. College of Engineering,Ocean University of China,Qingdao 266100,China; 2. Henan Key Laboratory of Underwater Intelligent Equipment,Zhengzhou 450015,China; 3. Shandong Marine Intelligent Equipment Technology Engineering Research Center,Qingdao 266100,China)

With the development of lightweight and agile undersea vehicle manipulator systems(UVMSs),the demand for high-precision underwater attitude control is becoming increasingly prominent. Euler angle is traditionally used to represent the attitude; however,an inverse kinematic solution under a special attitude results in a singularity when this representation is employed. As a result,the requirements of special operations cannot be fulfilled through this representation. In this study,therefore,the quaternion is used to represent the posture of the rigid body of an undersea vehicle,and a quaternion-based kinematics model is established to avoid the gimbal lock. Furthermore,a dynamic model for the UVMS,sliding mode surface based on quaternion error,and position and attitude sliding mode controller are established. The stability of the system is analyzed by the generalized Lyapunov theory. In order to achieve a better control effect,this study uses the function of integrate time absolute error(ITAE) to design the fitness function and uses the genetic algorithm(GA) to optimize the controller parameters. The simulation results verify the effectiveness of the controller.

undersea vehicle manipulator system; quaternion feedback; sliding mode control; genetic algorithm; parameters optimization

TP241; TJ630.32

A

2096-3920(2021)04-0407-08

10.11993/j.issn.2096-3920.2021.04.006

杜晓玮,侯冬冬,王红都,等. 基于四元数反馈的UVMS滑模控制器设计[J]. 水下无人系统学报,2021,29(4): 407-414.

2020-10-20;

2020-11-12.

河南省水下智能装备重点实验室开放基金(KL02A1802); 中央高校基本科研业务费专项(201964012).

杜晓玮(1995-),女,在读硕士,主要研究方向为水下机器人-机械手系统建模与运动控制.

(责任编辑: 许 妍)