金属蜂窝夹层结构抗水下爆炸特性*

魏子涵，赵振宇，叶 帆，裴轶群，王 昕，张钱城，卢天健

（1.西安交通大学机械结构强度与振动国家重点实验室，陕西 西安 710049；2.南京航空航天大学多功能轻量化材料与结构工信部重点实验室，江苏 南京210016；3.南京航空航天大学机械结构力学及控制国家重点实验室，江苏 南京210016；4.中国船舶及海洋工程设计研究院，上海200011；5.上海船舶工艺研究所，上海200032）

随着各类水下武器爆炸威力的提升，舰船在现代战争中的生存环境日趋恶劣，海上作战的保障能力受到前所未有的挑战，舰船结构的抗爆抗冲击能力成为衡量舰船生命力最重要的技术指标，如何提升舰船的防护能力是各国海军的研究重点[1]。

舰船底部是主机、武器装备等的工作平台，也是容易遭受水下武器攻击的重点部位，底部结构的抗水爆性能对舰船生命力尤其重要。目前，舰船水下外板的单元形式多为加筋板架结构，与其相关的研究开展相对较早，研究成果也较为丰富[2-8]。然而，承受水下爆炸载荷时，由于船底结构的加强筋较强，加强筋与面板变形的量值不一致：面板会出现较大的局部凹陷，冲击载荷较强时面板发生撕裂破坏，而加强筋不完全破坏[9]，结构本身的防护性能未得到充分发挥。在这种情况下，金属夹层结构以其轻质、高强、高效吸能、可设计性强等优点成为一种新型的舰船防护结构，引起了广泛关注。以金属四方蜂窝夹层结构为例，相关研究包括理论、模拟及实验3个方面。理论和模拟方面，Fleck 等[10]将夹层结构在爆炸冲击载荷作用下的响应过程分为流固耦合、芯体压溃和整体弯曲/拉伸变形3 个阶段。张延昌等[11]、王自力等[12]以某舰船中部双层船底板架结构单元为研究对象，研究了四方蜂窝夹层板在水下爆炸冲击波作用下的变形损伤、能量吸收及运动响应，发现蜂窝夹层板在水下冲击波作用下的最大变形仅是等质量传统加筋板架结构的2/3～1/3，在一定程度上改善了冲击环境，具有优越的防护性能。Xue等[13]对比了几种不同芯层的夹层结构在水下爆炸冲击波载荷下的位移响应，在载荷冲量相同时，发现四方蜂窝和波纹夹芯结构的后面板位移小于等质量的实心金属面板和三维金字塔点阵夹芯结构。实验方面，Wadley 等[14]设计了圆柱形水下爆炸冲击波模拟装置，对四方蜂窝夹层板在水下冲击波作用下的响应展开了实验研究，并与有限元分析结果进行对比，揭示了结构的变形过程和破坏模式。此外，Mori 等[15]、任鹏[16]采用非药式水下冲击波加载装置，开展了蜂窝夹层结构在水下爆炸冲击波作用下响应的实验研究。然而，上述研究中多采用简化装置近似模拟水下爆炸冲击波载荷，受限于实验装置，试件尺寸较小，且多为圆形，无法真实地反映应用于舰船的夹层结构在实际冲击环境（舰船水下爆炸）下的动态响应。因此，有必要开展相关的水下实爆实验，以更进一步探究蜂窝夹层板的防护性能。

本文中，以背板加筋的金属四方蜂窝夹层结构为研究对象，首先设计并制造样件，制定相应的水下实爆实验方案并进行实验。随后，通过实验和有限元相结合的手段进一步研究结构的变形模式和动态响应，量化载荷参数和关键几何参数对结构防护性能的影响。最后，以结构面密度和后面板变形的无量纲量为目标函数，对结构进行多目标优化设计，得到对应的Pareto前沿。

1 实验设计

1.1 实验方案

水下实爆实验布置如图1所示，此实验在露天水池中开展，实验使用的药包为TNT球形装药。为减少气泡载荷对结构动态响应的影响，药包侧面正对蜂窝夹层结构爆炸。由于实验场地的尺寸足够大，忽略水池边缘及底部反射的冲击波对结构响应的影响。

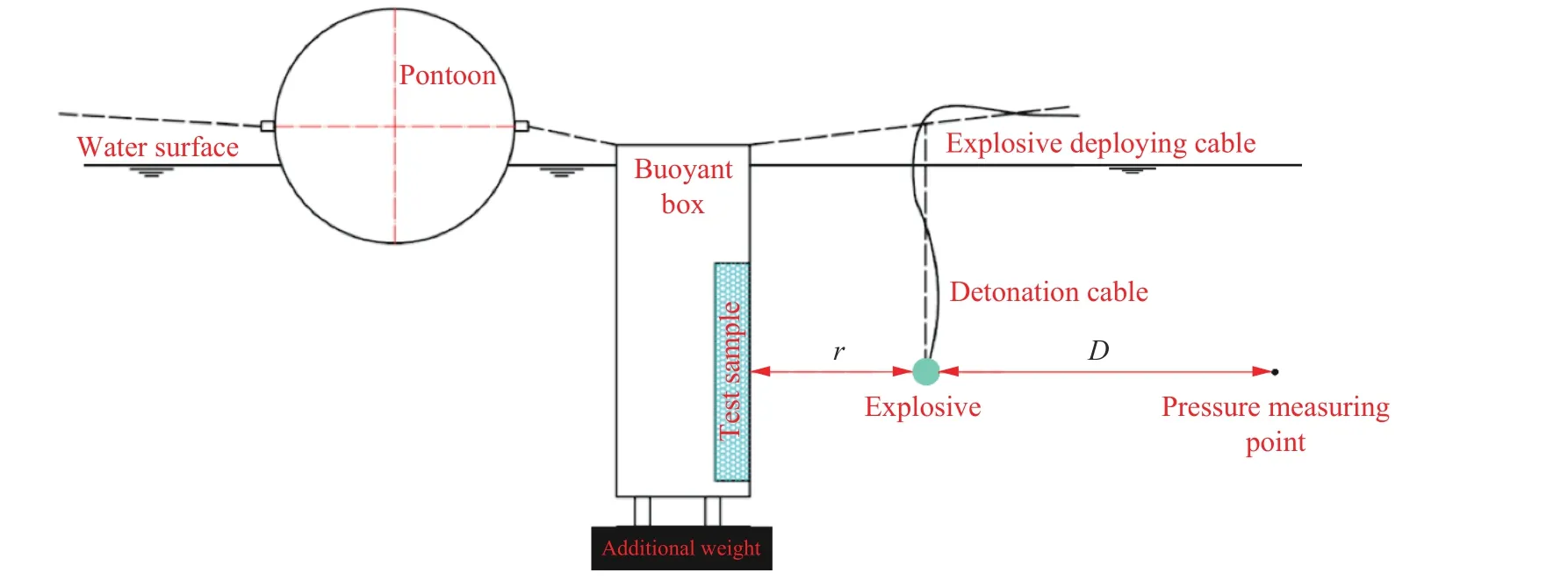
图1 水下爆炸实验布置Fig.1 Layout of underwater explosion experimental setup

实验装置包括浮筒、绳索、配重、试样、药包布防绳、起爆缆等。其中，浮筒不仅用于帮助调整浮箱位置，还可在试样出现破损时起到保护作用，确保装置能顺利地入水和出水；浮箱是实验的基础平台，其详细尺寸及作用将在1.3节叙述；配重通过缆绳与浮箱连接，主要用于调整整个实验装置的重心位置及重力，进而调整吃水深度及浮态；药包布放绳用于布放TNT 药包。本实验的TNT当量W为5 kg，爆距r为3.2 m，TNT 药包中心置于水深2 m 处。此外，在与药包水平相距D=6 m 处（压力测点处）布放一个压力传感器，用于测量水下爆炸冲击波的压力时程曲线。

1.2 实验样件

实验样件由蜂窝夹层板、加筋板及T形梁等3部分组成，长2.24 m，宽1.50 m,如图2所示。图3给出了蜂窝夹层板及其代表性体积单元的示意图。将迎爆面面板定义为前面板，背爆面面板定义为后面板，则蜂窝夹层板由前/后面板、四方蜂窝芯体及四周的封板组成。前/后面板的材料选用船用高强钢，蜂窝芯体及封板的材料选用304不锈钢，两种钢材的密度相同，用ρ表示。前/后面板长a=1.38 m，宽b=1.00 m。前面板厚度w1= 6 mm，后面板厚度w2= 3 mm。蜂窝芯体高度Hc=60 mm，芯板及四周封板的厚度wc= 0.8 mm，蜂窝芯体的单胞长度L= 83 mm。蜂窝芯体的相对密度 ρ ¯c及蜂窝夹层板的面密度M¯ 可分别表示为：

本实验样件的芯体相对密度ρ¯c为0.019，蜂窝夹层板的面密度M¯为79 kg/m2。为便于蜂窝夹层板与浮箱相连接，在其前面板的上下缘焊接有衬板，如图2所示。蜂窝芯体由格栅方形条拼接而成，格栅方形条之间通过激光焊接连接，如图4所示。前/后面板与蜂窝芯体之间的连接同样通过激光焊接完成，封板与蜂窝夹层板之间则通过氩弧焊焊接。蜂窝夹层板的外围为传统加筋板架结构（舰船底部结构）。采用气体保护焊焊接加筋板和T形梁，其中加筋板的加筋为L形钢，其腹板高92 mm、厚6 mm，翼板宽24 mm、厚9 mm。T形梁分为横向和纵向两种。与加筋板面板相连接的横向T 形梁（见图2），其腹板高200 mm、厚6 mm，翼板宽100 mm、厚8 mm。与蜂窝夹层板后面板相连接的横向T 形梁和纵向T形梁（见图2），其腹板高为137 mm，其余尺寸不变。

图2 实验样件Fig.2 A sample for underwater explosion experiment

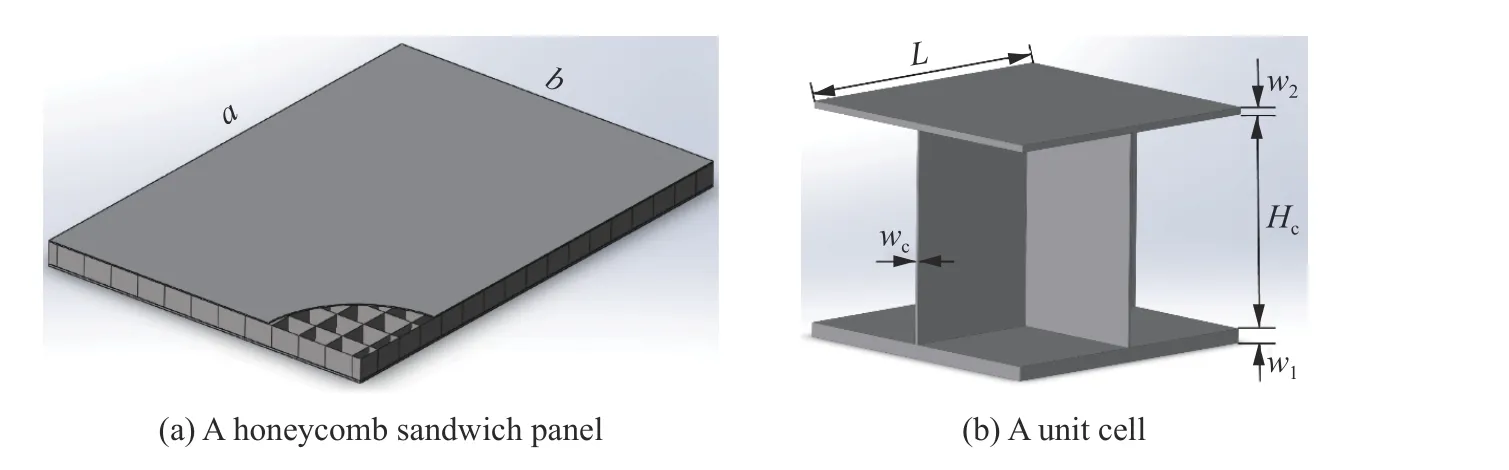
图3 蜂窝夹层板及其代表胞元示意图Fig.3 Schematics of a honeycomb sandwich panel and its unit cell

图4 四方蜂窝芯体的制备Fig.4 Fabrication of square honeycomb cores

1.3 实验浮箱设计

本次实验的爆距较近，为减小水下爆炸产生的气泡对结构响应的影响，实验设计为TNT药包侧面正对样件爆炸。由此设计了对应的浮箱，浮箱为长2.0 m、高3.3 m、宽1.0 m 的长方体箱体结构，材料选用304不锈钢，浮箱的面板厚度为12 mm。为防止浮箱在爆炸冲击波作用下产生破坏，在浮箱周围焊接有宽120 mm、厚12 mm 的加强筋，其空间分布如图5所示。实验时，为防止水下爆炸产生的水柱从上方灌入浮箱，在浮箱上加封盖。在浮箱侧面留置开口，以便将其与试样连接。浮箱与试样之间通过32个M10螺栓连接；为保证水密性，在浮箱与试样之间设置橡胶垫圈。为保证试样四周的边界条件一致，在开口上侧的样件与浮箱连接处焊接有隔板，隔板上同样焊接有加强筋。另外，在开口上、下侧各焊接有3 个工字钢，以便在样件变形时对样件的边界部分起到支撑作用，从而防止样件与浮箱之间的连接螺栓被剪断。本次实验中，浮箱的主要功能如下：（1）作为支撑平台，对试样起到一定的固定作用，同时使得后者达到并保持在预定的水下位置；（2）内空的盒体结构为试样提供背空的边界条件；（3）保证实验的水密性。

图5 浮箱示意图Fig.5 Schematic of thebuoyant box

2 数值模拟

为进一步研究背板加筋金属蜂窝夹层结构在水下爆炸载荷作用下的变形过程及载荷、几何参数对其防护性能的影响，本节通过商业有限元分析软件Abaqus/Explicit，采用声固耦合算法对结构的动态响应进行数值模拟。

2.1 有限元模型

采用声固耦合法进行水下爆炸冲击响应分析时，把流体描述为一种声学介质，冲击波在声学单元中传播：流体网格仅起到传递压力的作用，不会产生位移，也不会因为爆炸快速膨胀或流体单元的压缩而产生大变形，由此可显著节省计算资源，且计算相对稳定，因此该方法在工程领域广为应用[17]。使用声固耦合法分析水下爆炸问题，可采用Abaqus提供的两种方法：总波公式和散波公式。相较于散波公式，总波公式可考虑流体的空化效应及流体静压对结构响应的影响。本文中采用总波公式，流体的空化临界压力设置为0 MPa。图6给出了有限元模型的示意图，模型由3个子结构构成，即水域、浮箱及样件。建模时，浮箱及样件的几何尺寸与实际一致，但对样件的蜂窝芯体做简化处理，即忽略格栅方形条的平台及折弯部分，仅对方形条的纵板进行建模，并假设样件各部分之间为理想连接。水域的长宽均为7 m，高为8 m。模型的吃水深度（2.825 m）与实际实验的取值相同。爆炸源点（source point，即TNT药包球心，见图6）选取在水域之外水平正对样件中心相距3.2 m 处（r=3.2 m），爆距点（standoff point）选取在流体-结构耦合面上距离爆炸源点最近的点（即样件前面板的中心点，见图6）。水域的上表面为自由边界，其余几个表面设置为无反射边界。通过绑定(tie)接触，将样件与浮箱之间的连接设置为理想绑定连接。网格划分方面，采用AC3D4声学四面体单元对水域进行网格划分，流体-结构耦合面处的网格较密，网格尺寸设置为8 mm；水域外表面的网格则较稀疏，网格尺寸设置为60 mm。采用S4R 壳单元对样件和浮箱进行网格划分，为确定结构的网格尺寸，对比了采用不同网格尺寸计算得到的前面板中心点变形，如图7所示。可见，网格尺寸选取为8 mm 时，进一步加密网格对结构变形影响不大，因此后续计算中选取的网格尺寸均为8 mm。

图6 有限元模型Fig.6 Finite element simulation model

图7 网格收敛性分析Fig.7 Mesh convergence analysis

2.2 材料参数

采用双线性弹塑性模型模拟构成蜂窝芯体和浮箱的304不锈钢，材料参数依次为：密度，7 850 kg/m3；弹性模量，210 GPa；泊松比，0.3；屈服应力，200 MPa；塑性强化阶段的切线模量，2 GPa。304不锈钢为应变率相关材料，其动态屈服强度与应变率之间的关系[18]为：

式中：σd和σ0分别为材料在一定塑性应变下的动态 屈 服强 度 和 准 静态 屈 服强 度，εpl和ε ˙pl分 别为塑性应变和应变率；K为应变率相关因数，其值引自文献[19]并在表1中给出。采用理想弹塑性材料模型模拟构成样件面板等其他部分的船用高强钢，相关材料参数为：密度，7 850 kg/m3；弹性模量，181 GPa；泊松比，0.3；屈服应力，400 MPa。此外，定义水的体积模量为2.082 GPa，密度为1 000 kg/m3，声波在水中的传递速度为1 500 m/s。

表1 304不锈钢的应变率参数[19]Table 1 Strain-rate parametersof 304 stainlesssteel[19]

2.3 水下爆炸载荷

实验过程中，水下爆炸冲击波对样件的变形和破坏过程起主导作用。前人基于大量的理论分析及实验研究总结出了爆炸冲击波的计算公式。其中，TNT 球形炸药水下爆炸时产生的冲击波压力可通过以下半经验公式[20-21]求解计算：

式中：p(t)为冲击波压力，Pa；pm为冲击波压力峰值，Pa；θ 为时间衰减常数，表示冲击波压力从峰值压力pm下降至pm/e所需的时间，s；tp为冲击波正压载荷作用时间，s；W为TNT 药包质量，kg；r为测点距爆心的距离，m；r0为TNT 球形装药的药包半径，m；r¯为爆距与药包半径之比r/r0；c为水中声速，一般取1 500 m/s；p¯0为TNT 装药爆心处流体静水压强与大气压之比。

图8给出r=6 m 处压力测点的冲击波压力时程曲线的实验及理论结果，两者吻合良好。有限元计算时，输入载荷为r= 3.2 m 爆距点处冲击波压力的理论值，峰值压力为25.81 MPa，时间衰减常数为0.17 ms。

图8 压力测点处冲击波压力时程曲线Fig.8 Shock wave pressure-time curves at thepressure measuring point

3 结果与讨论

3.1 实验及模拟结果分析

图9给出蜂窝夹层样件在水下爆炸冲击波载荷作用下前/后面板中心点变形时程曲线的模拟结果。实验后经过测量，样件前/后面板中心点的最终塑性变形分别为123.4和119.1 mm，与之对应的模拟结果为120.5和120.0 mm，模拟计算的蜂窝芯体压缩变形较实验结果稍小，其原因是模拟计算中对蜂窝芯体做了简化，忽略了格栅方形条折弯过程中产生的初始变形缺陷，导致芯体的压皱峰值载荷有所增加。

图9 样件前、后面板中心点变形时程曲线Fig.9 Deformation-time curves at the central points of the front and back faces of the sample

通过模拟计算，图10给出样件（纵向二分之一模型）的变形过程。爆炸冲击波作用于结构后的t=2.4 ms时刻，由于浮箱上工字钢的支撑作用，蜂窝芯体首先在上下边缘区域发生压剪变形。随着时间的推移，芯体剪切区域逐渐向面板中心移动，t= 7.7 ms时结构达到最大变形，随后发生小幅度的弹性振荡，塑性变形则基本稳定。图11给出样件的整体变形实物图，图12则给出其横向、纵向剖面的模拟和实验变形对比，可见模拟和实验结果的吻合度较好。实验后，蜂窝夹层板的前、后面板未产生撕裂等损伤，前面板主要受到入射冲击波、芯体及边界约束的共同作用，产生弯曲和拉伸变形。在T 形梁的横向载荷、前面板传递的压力载荷、后面板的支撑力以及边界约束的共同作用下，边界部分的芯体发生较为明显的压皱与剪切变形；在前面板传递的压力及后面板提供的支撑力作用下，中间区域的芯体发生芯体剪切屈曲，但变形程度小于边界区域。后面板的上下边缘在工字钢支撑处有明显的凹陷痕迹，在左右边界区域受到T 形梁、芯体及边界条件的共同作用而发生明显的局部凹陷变形，以T 形梁焊接位置处变形最大，中心区域的后面板则受到芯体作用，发生拉伸与弯曲变形。

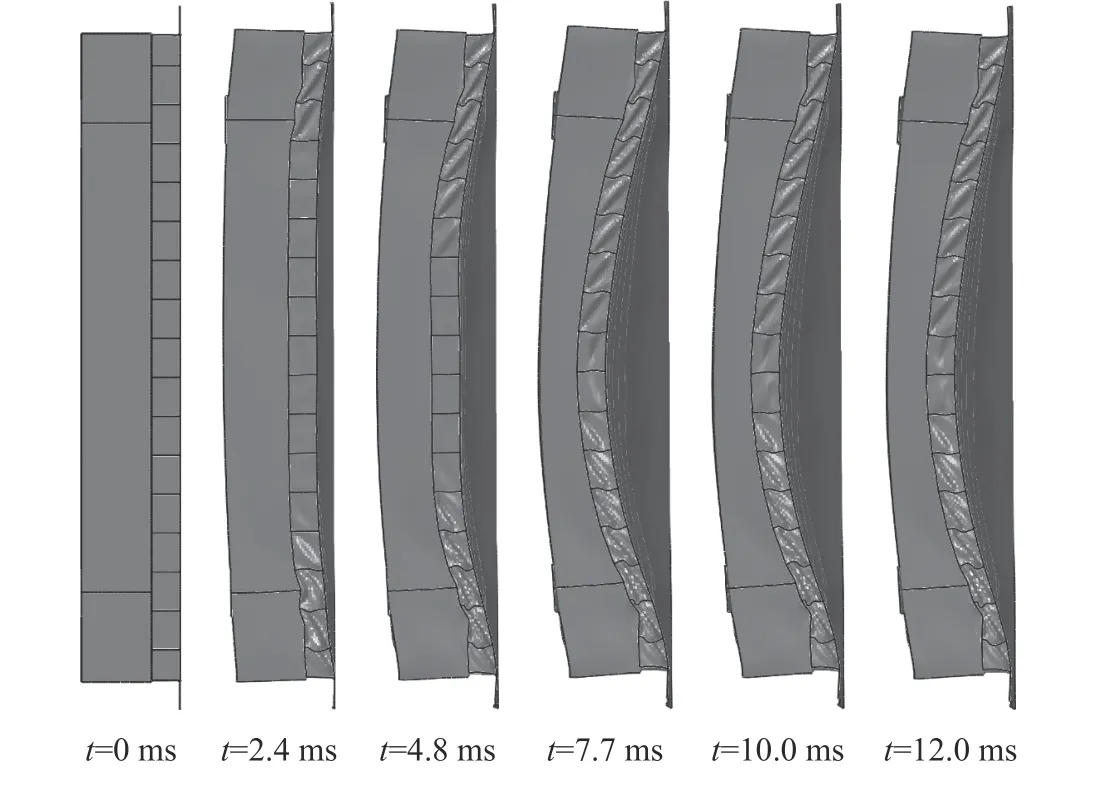
图10 水下爆炸载荷作用下样件变形过程模拟结果Fig.10 Simulated deformation process of thesample subjected to underwater explosion

图11 样件整体变形Fig.11 Overall deformation of thesample after underwater explosion

图12 试样剖面变形模拟结果与实验结果的对比Fig.12 Comparison of simulated and experimental profiledeformations of thesample

基于数值模拟，图13分别给出蜂窝夹层板前、后面板中心点的加速度时程曲线：可见，加速度响应为非线性很强的高频振荡曲线，相对于前面板，后面板的加速度峰值更低、曲线的振幅更小。该结果对保护舰船上的重要仪器设备具有指导意义。图14给出蜂窝夹层板在变形过程中，各个子结构及整体的塑性变形能量吸收曲线：可见，吸能效率较高的蜂窝芯体吸收了大部分能量，约占整个蜂窝夹层板吸收能量的69%；前面板和后面板吸收的能量相近，各自约占总吸收能量的16%。

图13 蜂窝夹层板前、后面板中心点的加速度时程曲线Fig.13 Acceleration-time curves at the central points of the front and back faces of the honeycomb sandwich panel

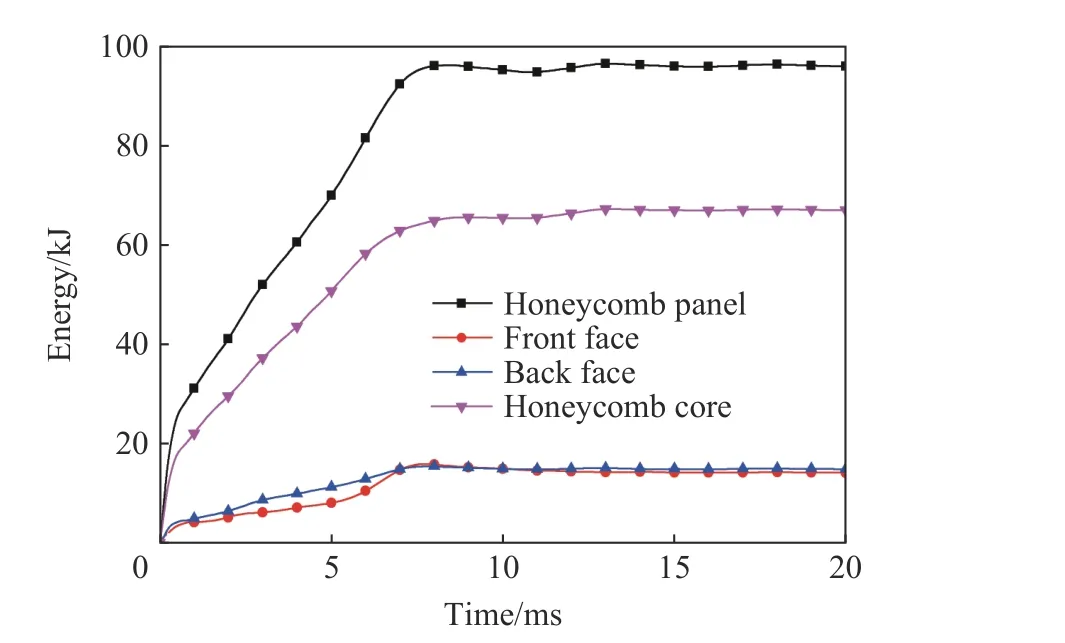
图14 蜂窝夹层板及其构成结构的能量吸收曲线Fig.14 Energy absorption curves of the honeycomb sandwich panel and itsconstituting sub-structures

3.2 载荷参数影响分析

为在更普遍意义上表达各种工况爆炸产生的冲击波对结构的影响，定义冲击因子φ[22]为：

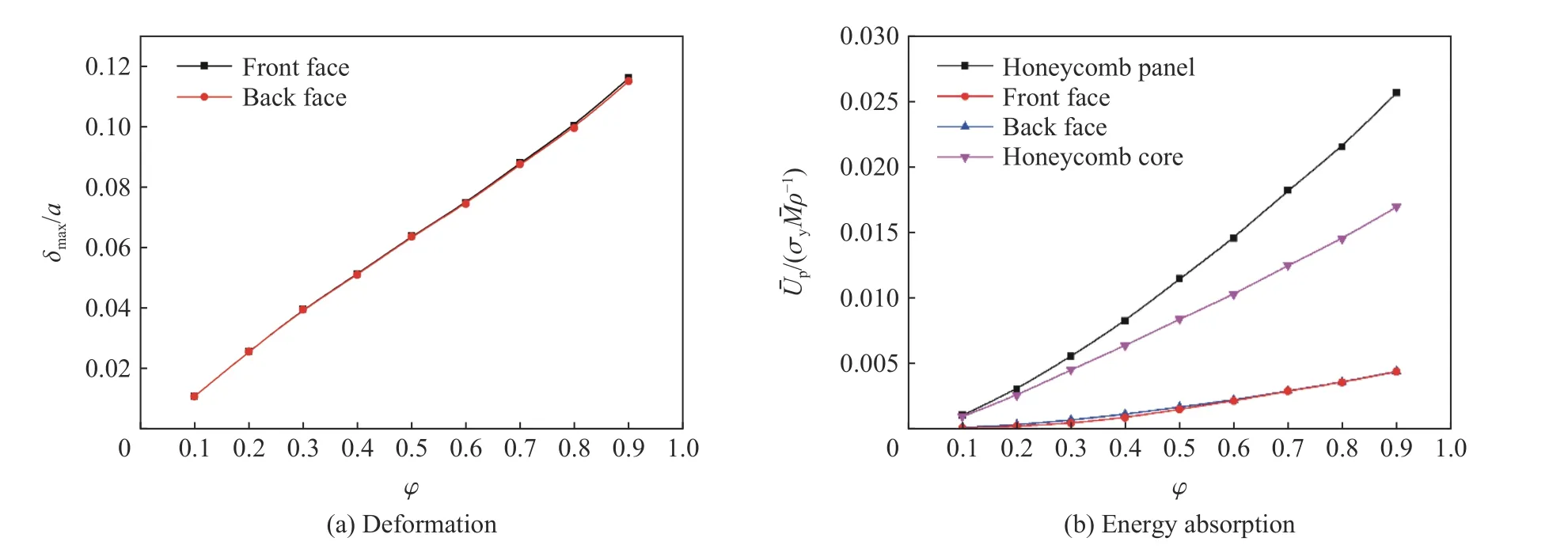
图15 冲击因子对夹层板变形及能量吸收的影响Fig.15 Effect of the impact factor on deformation and energy absorption of sandwich structures

图16 不同的冲击因子对应的结构截面变形示意图Fig.16 Cross-sectional morphologies of sandwich structures subjected to underwater explosion for different impact factors

3.3 结构参数影响分析

在爆炸载荷不变的前提下，改变前面板厚度w1、后面板厚度w2以及芯板厚度wc，保持其余几何参数与实验样件一致，研究了前/后面板厚度比w1/w2以及芯体相对密度ρ¯c对结构动态响应的影响。改变前/后面板厚度比时，芯体相对密度保持为0.019；改变芯体相对密度时，前/后面板厚度比保持为2。参数改变时，蜂窝夹层板的总质量保持不变。图17(a)给出δmax/a随前/后面板厚度比的变化曲线，可见前/后面板的最大变形随w1/w2的增大先降低后升高。w1/w2对结构纵向截面变形的影响如图18所示，结果表明改变w1/w2对芯体变形模式的影响不大，但对前面板的变形模式有一定影响。w1/w2为0.25或0.50时，前面板的厚度较小，在冲击波直接作用下，前面板在蜂窝单胞构成的空腔区域发生了局部弯曲，因此此时前、后面板最大变形的差值较大。随着w1/w2的增大，前面板不再发生局部弯曲，当w1/w2取1.00（即前/后面板厚度相同）时，结构的最大变形取得极小值，如图17(a)所示。图17(b)给出芯体相对密度对结构前/后面板中心点最大变形的影响曲线：与w1/w2的影响曲线类似，前/后面板最大变形随着ρ¯c的增加先降低后升高。图19给出几组不同ρ¯c取值下结构纵向截面变形的示意图。ρ¯c=0.005时，蜂窝芯板厚度较小，芯体的压皱峰值载荷较低，更容易被压皱，因此前后面板之间最大变形量的差值最大，芯体的压皱程度最高，此时前/后面板的变形也最大。随着ρ¯c的增加，芯体压皱峰值载荷逐渐提升，压皱程度逐渐降低，ρ¯c=0.060时，结构的变形取得极小值，此时的蜂窝芯体几乎无压皱变形。随着ρ¯c的进一步增大，蜂窝芯体的变形以整体弯曲为主，前面板开始发生局部弯曲变形，前后面板最大变形之间的差值开始升高，结构的变形量增大。相较于前后面板厚度比，芯体相对密度对结构变形的影响更大。

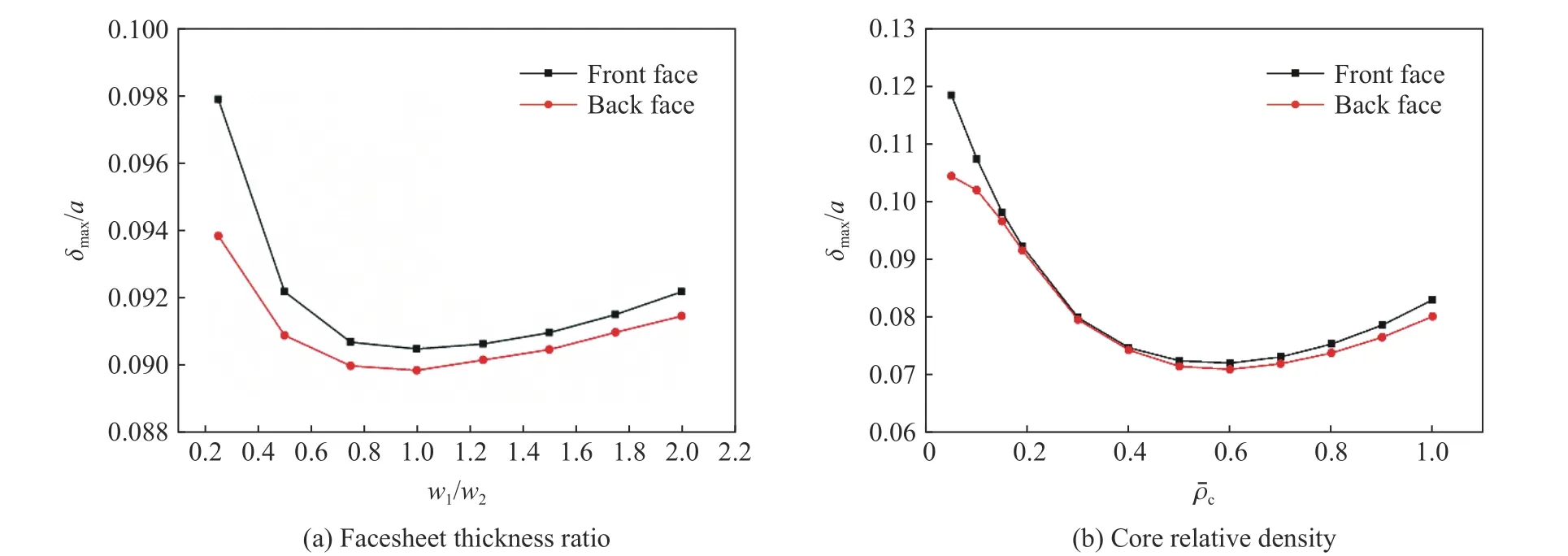
图17 前后面板厚度比和芯体相对密度对结构变形的影响Fig.17 Effect of thefacesheet thickness ratio and core relativedensity on deformation of sandwich structures

图18 不同前/后板厚度比对应的结构截面变形示意图Fig.18 Cross-sectional morphologies of sandwich structures subjected to underwater explosion for different facesheet thickness ratios

图19 不同芯体相对密度对应的结构截面变形示意图Fig.19 Cross-sectional morphologies of sandwich structures subjected to underwater explosion for different core relative densities

4 优化设计

蜂窝夹层结构具有很强的可设计性。在相同的水下爆炸冲击波载荷作用下,采用不同几何参数设计的蜂窝夹层结构呈现差异很大的防护性能。为在整个设计空间内获得抗爆性能最优的蜂窝夹层结构，有必要开展进一步的优化设计。通过商业数学软件Matlab R2016a 对蜂窝夹层结构展开多目标优化设计，流程如图20所示。

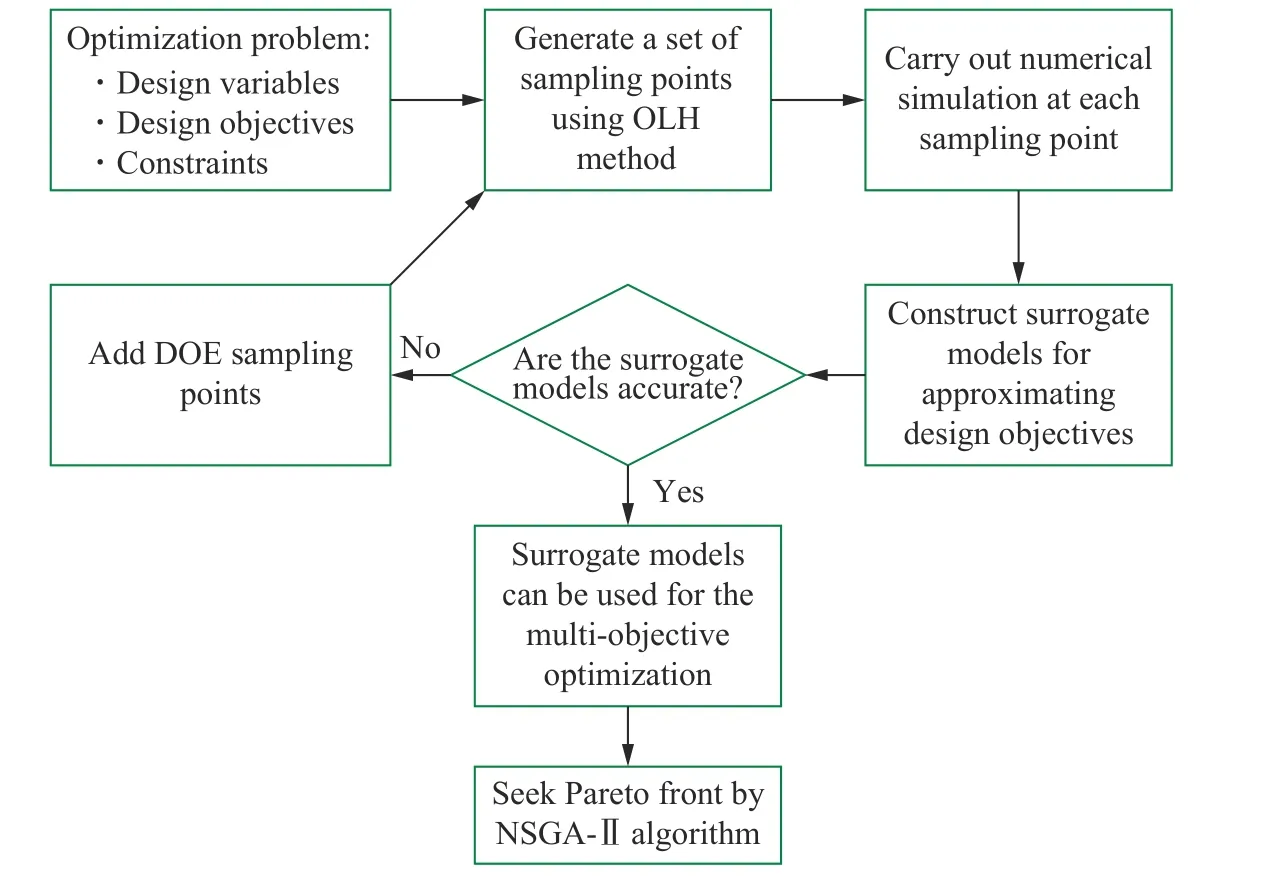
图20 优化流程图Fig.20 Flow chart of optimization methodology

4.1 多目标优化问题的建立

在对蜂窝夹层结构进行优化时，选取前面板厚度、后面板厚度以及芯板厚度的无量纲量为设计变量，分别表示为w1/Hc、w2/Hc和wc/Hc，其中，前/后面板厚度的取值范围为1.0～8.0 mm，对应无量纲量取值范围为0.017～0.133，芯板厚度的取值范围为0.4～4.0 mm，对应无量纲量取值范围为0.007～0.067，其余的几何参数保持与实验样件相一致。为使得蜂窝夹层结构在变形尽可能小的同时具有尽可能小的质量，以蜂窝夹层板后面板中心点变形最大值无量纲量δmax/a和面密度无量纲量M¯/(ρHc)为目标函数。其中，M¯的表达式在式(2)中给出。由于实验模型的复杂性以及水下爆炸问题本身的非线性，获取δmax/a的解析式比较困难，因此，在本优化问题中，选用代理模型法来近似拟合其表达式，具体细节在4.2节给出。根据设计变量、约束条件及目标函数可以确定本多目标优化的数学模型：

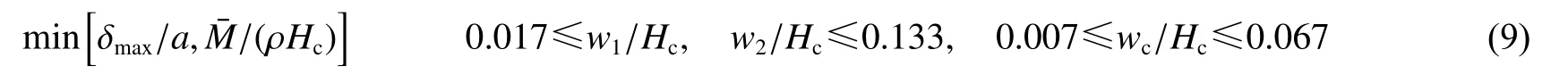
4.2 实验设计及代理模型

实验设计（design of experiments,DOE）是结构优化设计中重要的统计方法，其主要内容是讨论如何合理地安排实验、取得数据，然后进行综合的科学分析，从而达到尽快获得最优方案的目的[24]。优化拉丁超立方实验设计（optimal Latin hypercube,OLH）是一种典型的实验设计方法，它能使采样点均匀的散布在整个设计空间，同时考虑了采样点之间的正交性，使得模拟方案具备较好的典型性和代表性[25]。本节采用这种方法进行采样，共选取60 个样本点进行有限元模拟，得到每个点对应的位移响应，相应结果如表2所示。

表2 采样点及其对应的有限元模拟结果Table 2 Sampling points and corresponding numerical results

径向基神经网络代理模型（简称RBF模型）具有能以任意精度逼近非线性函数、近似能力好、应用价值高等特点，被广泛应用于优化设计[26]。本节采用该方法构造代理模型。为验证代理模型的准确性，对决定系数（R2）、均方根误差（erms）和最大绝对百分比误差（emap）进行了计算：

式中：yi、、分别为模拟结果、模拟结果的平均值和代理模型的预测值，N为采样点的个数。本文代理模型的确定系数为0.980 5，均方根误差为0.030 6，最大绝对百分比误差为0.109 1，均在可接受范围内，表明此代理模型可准确表示目标函数δmax/a与设计变量w1/Hc、w2/Hc和wc/Hc之间的关系。

4.3 基于NSGA-Ⅱ算法的多目标优化

在成功构建代理模型之后，本节采用非支配排序遗传算法（NSGA-Ⅱ）求解多目标优化问题。NSGA-Ⅱ算法具有运算速度快、计算复杂度低、易于实现等优点，已成为最常用的多目标优化算法之一[27-28]。由于多目标优化问题中各目标函数之间通常是相互冲突的，故在求解此类问题时，最优解并非唯一，而是一个解集，称为Pareto最优解集，而Pareto最优解集在目标函数空间中的像称为Pareto前沿。本文采用NSGA-Ⅱ算法进行优化时，设置的种群数量为100，最大迭代次数为500，最终优化出的Pareto前沿如图21所示。对两目标函数δmax/a和M¯/(ρHc)通过多项式进行拟合，拟合结果为：

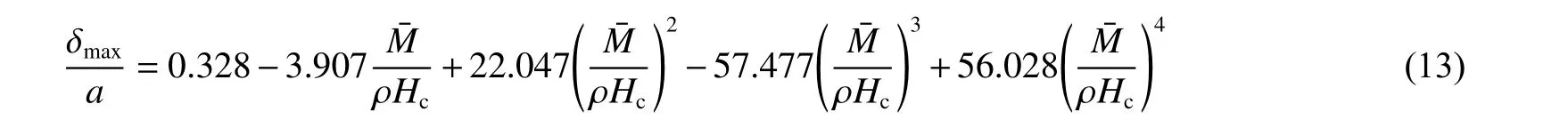
此多项式拟合的确定系数（R2）为0.999 8，足以说明其准确性。为验证上述优化结果的准确性和有效性，从Pareto前沿选取4个代表点，对其代表的结构进行模拟计算，表3对比了模拟与优化结果，可见两者之间误差小于3%，表明优化结果可靠。本文原实验结构的面密度无量纲量M¯/(ρHc)为0.167，后面板中心点的变形最大值无量纲量δmax/a为0.092。为了对优化后的结构与原结构进行对比，在图21中标出了实验样件所对应的点。从图中可以看出，点3在与实验样件拥有相同的后面板中心点最大变形的情况下，面密度相对实验样件减少了31.1%，点4在与实验样件拥有相同的面密度的情况下，后面板中心点最大变形相对实验样件减少了26.1%。位于点3和点4中间的点相对原实验样件同时呈现出了更小的面密度和后面板变形，是原实验结构的支配解，而Pareto前沿其它区域的点是原实验样件的非支配解。图22给出了Pareto最优解集中3个设计变量w1/Hc、w2/Hc和wc/Hc与目标函数δmax/a之间的关系。在工程应用时，可首先根据设计需要，确定结构的面密度无量纲量M¯/(ρHc)或接受范围内的最大变形无量纲量δmax/a，随后于图中找出对应的结构参数，以获得相应的优化结构。例如，若确定设计结构面密度的无量纲数M¯/(ρHc)为0.15，可首先结合图21和式(13)求出优化结构对应的后面板最大变形无量纲量δmax/a，其值为0.072，接着通过图22找出对应的设计变量w1/Hc、w2/Hc和wc/Hc的取值，分别为0.051、0.052和0.035，进而得到防护性能最优结构的几何构型。此优化结果对蜂窝夹层结构的选型有一定的参考价值。

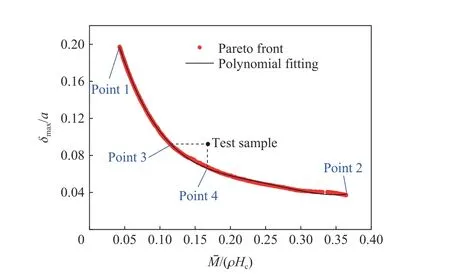
图21 多目标优化问题的Pareto前沿Fig.21 The Pareto fronts for the present multi-objective optimization problem

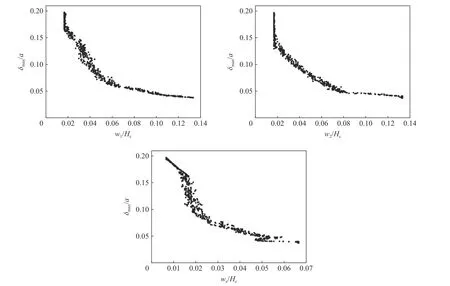
图22 最优解集对应的w1/H c、w2/H c 和w c/H c 与δmax/a 之间的关系Fig.22 Relationships of w1/H c,w2/H c and w c/H c with δmax/a obtained from corresponding optimization solutions

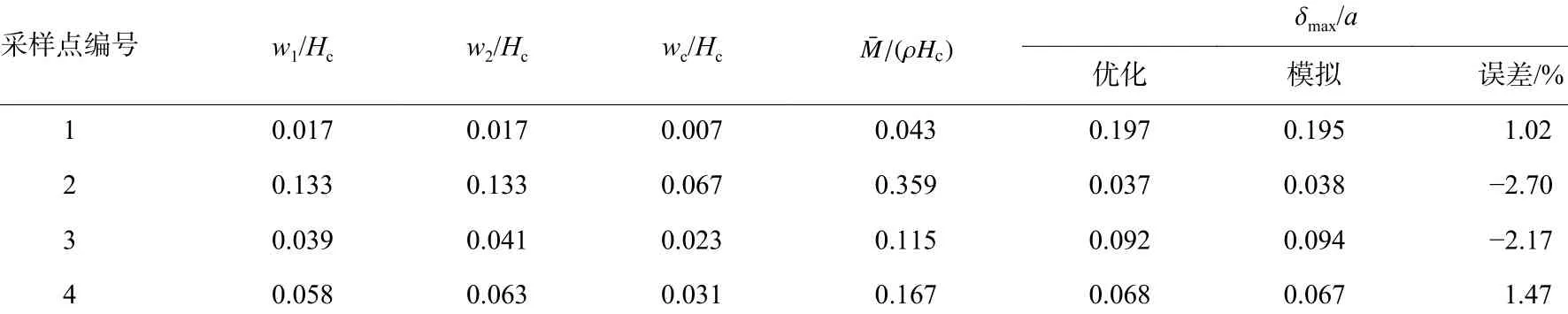
表3 优化结果与模拟结果的对比Table 3 Comparison between optimization solutionsand numerical results

5 结 论

为探究金属蜂窝夹层结构作为舰船水下防护结构的潜力，系统研究了背板加筋四方金属蜂窝夹层板在水下爆炸载荷作用下的动态响应特性及防护性能。首先，设计并制造了背板加筋蜂窝夹层结构试样及相应的浮箱，在大型露天水池中开展了水下实爆实验；随后，采用有限元模拟与实验相结合的手段研究了结构的水下爆炸响应，量化了载荷参数冲击因子及几何参数前后面板厚度比、芯体相对密度对结构响应和变形模式的影响；最后，通过NSGA-Ⅱ遗传算法对蜂窝夹层结构进行多目标优化，得到了对应的Pareto前沿。得到主要结论如下。

（1）水下爆炸载荷（TNT 药包质量W=5 kg，爆距r=3.2 m）作用下，背板加筋金属蜂窝夹层结构的芯体首先在上下边缘区域产生压剪变形，芯体压剪区域随后向面板中心移动，在7.7 ms时刻，蜂窝夹层结构的后面板达到最大变形，随后发生小幅度弹性振荡，塑性变形则基本稳定。

（2）水下爆炸后，蜂窝夹层结构的前、后面板未产生撕裂等损伤，前面板产生弯曲和拉伸变形；蜂窝芯体的主要部分发生剪切屈曲变形，在T形梁腹板对应的位置发生压剪变形；后面板的上下边缘受浮箱工字钢支撑处有明显的凹陷痕迹，左右边界区域发生明显的局部凹陷变形，在T形梁焊接位置处的变形最大，中心区域则发生与前面板类似的弯曲与拉伸变形。

（3）随着冲击因子的增大，蜂窝夹层板整体变形明显增大，蜂窝芯体始终是主要的吸能构件，但其吸能占比逐渐下降，前后面板在吸能方面的作用逐渐凸显。随着前后面板厚度比或芯体相对密度的增大，蜂窝夹层板前/后面板中心点的最大变形均呈现先降低后升高的趋势，同时呈现不同的变形模式。相较而言，芯体相对密度对结构变形的影响更显著。

（4）相较于原实验结构，以前后面板厚度及芯板厚度的无量纲量为设计变量，以蜂窝夹层板面密度和后面板中心点变形最大值的无量纲量为目标函数可实现多目标多参数优化，优化结构在相同最大变形下使面密度降低31.1%，在相同面密度下使最大变形降低26.1%。优化结果可为蜂窝夹层结构的设计选型提供参考。