高共面/异面抗冲击承载能力的新型蜂窝设计及吸能评估*

廖 就，李志刚，梁方正，王佳铭，刘婉婷，李 萌，冯建文

（1.北京交通大学机械与电子控制工程学院，北京 100044；2.中国空间技术研究院钱学森空间技术实验室，北京100094；3.中国民用航空适航审定中心，北京100102）

蜂窝结构由于其密度低、压缩变形能力强且变形可控等优点，被广泛应用于碰撞缓冲吸能领域。但蜂窝是一种各向异性结构，研究表明，常规铝蜂窝通常只在异面方向具有很好的承载能力，在共面方向承载很弱，异面承载性能远高于共面[1]。但在作为缓冲结构的实际应用过程中，承受的冲击载荷方向往往具有一定的不确定性，例如汽车的不同角度碰撞、直升机方向不确定的坠毁、城市安全岛防护等场景。在这些实际应用环境下，蜂窝除了要提供必要的异面承载能力之外，共面方向也要具备一定的强度，因此传统蜂窝共面异面承载能力差距大的问题就限制了蜂窝的实际应用。跟与蜂窝替代使用的泡沫结构相比，泡沫结构（如泡沫铝）虽具有近似各向同性的特征，能够多向承载，但是相比于蜂窝结构，泡沫铝是逐渐压实的过程，承载力曲线是逐渐上升，不能保持稳定的平台段；另外泡沫铝的有效压缩比与蜂窝相比更小，比吸能也相对要小。因此，本文的目标是设计高共面/异面抗冲击能力的新型蜂窝构型并对其吸能效果进行评估，提高共面/异面的蜂窝承载吸能比例。

目前在对蜂窝结构的研究中，主要集中在共面或异面某一个特定压缩方向下的分析。在异面方向的研究中，部分学者[2-4]通过理论研究的方式为蜂窝结构的缓冲设计提供思路，其中荣吉利等[2]基于超简化折叠单元理论，给出了六边形蜂窝异面压缩时的平台应力计算的理论公式。还有部分学者的研究聚焦在异面承载性能优良的新型蜂窝结构的设计上，何彬等[5]提出了一种基于菱形和圆形的新型蜂窝，通过在中高速冲击工况下与传统蜂窝进行对比，发现新型蜂窝异面承载能力和能量吸收能力较好。杜义贤等[6]提出了一种内部嵌套菱形结构的新型Y形周期性点阵结构，仿真结果表明该构型承载性能更加优越。Yang 等[7]在传统六边形蜂窝结构基础上引入马蹄形结构可以提升结构的异面承载能力和比吸能。王中钢等[8]、Wang 等[9]通过在六边形蜂窝内部合理布置加强筋，通过有限元仿真的方式研究了不等厚加筋对于正六边形蜂窝的异面承载能力影响，并且提出了两种新的加强蜂窝构型，分别是双六边形蜂窝以及内部圆加筋蜂窝，并建立了其平均压缩力和比吸能的理论模型，并通过仿真的方式加以验证，研究结果表明，新型加强蜂窝的平均压缩力和比吸能均优于传统六边形蜂窝和三角形蜂窝。

在蜂窝共面方向的研究中，胡玲玲等[10-11]研究了不同胞元构型和排列方式对蜂窝面内冲击力学性能的影响，发现不同的胞孔构型导致胞壁的受力状态不同，影响蜂窝的宏观力学性能。Liu 等[12]研究了冲击载荷作用对不同胞元微拓扑结构的动态冲击性能影响。何强等[13]建立了具有固定相对密度的分层屈服强度梯度圆形蜂窝模型，研究表明屈服强度梯度的变化使得蜂窝材料的局部变形模式发生变化，合理调节屈服强度梯度的变化可以减小初始峰值应力。为改善传统蜂窝共面方向承载能力较较弱的缺点，不少学者提出了共面承载能力优良的新型蜂窝。Hedayati 等[14]提出了一种新型的八角形蜂窝，并与传统构型蜂窝进行了比较，发现八角形蜂窝的屈服应力和弹性模量值与正六边形蜂窝相接近，且优于其他蜂窝；Thomas等[15]在铝合金蜂窝胞元内增加水平加强筋以提高其刚度，采用试验和仿真的手段研究了这种加强型六边形蜂窝的共面刚度和耗能性能。也有学者采用具有负泊松比的胞元构建新型蜂窝，卢子兴等[16]采用数值方法，研究了负泊松比蜂窝在不同冲击速度下的变形模式和能量吸收等动力学响应特性。Hu 等[17]对比了负泊松比的内凹六边形蜂窝与传统六边形蜂窝的面内刚度，发现等壁厚的内凹六边形蜂窝的刚度高于六边形蜂窝，但在等相对密度的前提下，内凹六边形蜂窝的泊松比绝对值必须大于特定值时，才有更高的面内刚度。马瑞君等[18]提出了一种新型改进内凹六边形蜂窝，通过数值仿真研究发现该构型具有三维负泊松比特性，该性能使蜂窝在共面压缩时具有更高的平台应力。

上述关于蜂窝的研究基本上都集中在蜂窝单一方向的承载能力，尚缺少同时兼顾共面和异面两个方向承载能力的研究。因此本文提出了3种新的高共面/异面抗冲击承载能力的新构型蜂窝，并对它们共面及异面的的承载能力进行了仿真评估，研究成果可为多方向载荷冲击下蜂窝结构设计提供参考依据。

1 新构型蜂窝设计

本节提出了3种高共面/异面抗冲击承载能力的新构型蜂窝。

1.1 胞壁弓字形弯折蜂窝

传统六边形蜂窝承受共面压缩时仅依靠胞壁从折痕处折叠弯曲来吸能，内部孔隙无支撑导致共面方向承载能力很弱，直接导致蜂窝结构的共面异面承载能力差距很大。因此，本构型以传统六边形蜂窝为出发点，将初始竖直胞壁每隔一段距离a向内部进行一次弯折，弯折长度为x，弯折的深度确保三部分弯折胞壁可以相互接触，从而能够在共面方向上相互支撑而承载吸能，模型的胞元边长为l，壁厚为t，高度为h，设计思路如图1所示。该蜂窝一方面以诱导变形思路规范了蜂窝异面压缩时的变形次序，另一方面内部折叠胞壁形成共面支撑肋板，承受共面压缩时，可以提供有效支撑，以提升共面方向的承载能力，最后达到缩小共面和异面承载能力差距的设计目的。

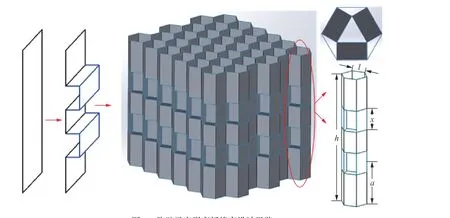
图1 胞壁弓字形弯折蜂窝设计思路Fig.1 Design of the bow-shaped honeycomb

1.2 层间组合蜂窝

传统蜂窝构型的胞壁均沿异面一个方向进行扩展延伸，这样的结构具有单一方向性的特点，导致蜂窝共面方向和异面方向承载能力具有较大的差距。因此本构型拟通过对蜂窝结构进行分层组合，使隔层蜂窝在空间中具备一定的交错角度来打破传统蜂窝结构的承载方向单一性，进而达到缩小共面异面承载能力差距的目的。考虑到六边形蜂窝的胞元边界之间相互有交叉，不容易实现层间组合的设计思路，因此本构型在设计时以传统的三角形蜂窝为出发点，隔层蜂窝在空间中交错90°，进而组合为一整体。本构型胞元边长为l，壁厚为t，模型高度为h，设计思路如图2所示，该层间组合蜂窝突破传统蜂窝胞壁结构方向的单一性，力求共面和异面方向上的承载结构趋同，最后达到缩小共面、异面方向上的承载和吸能差距的设计目的。

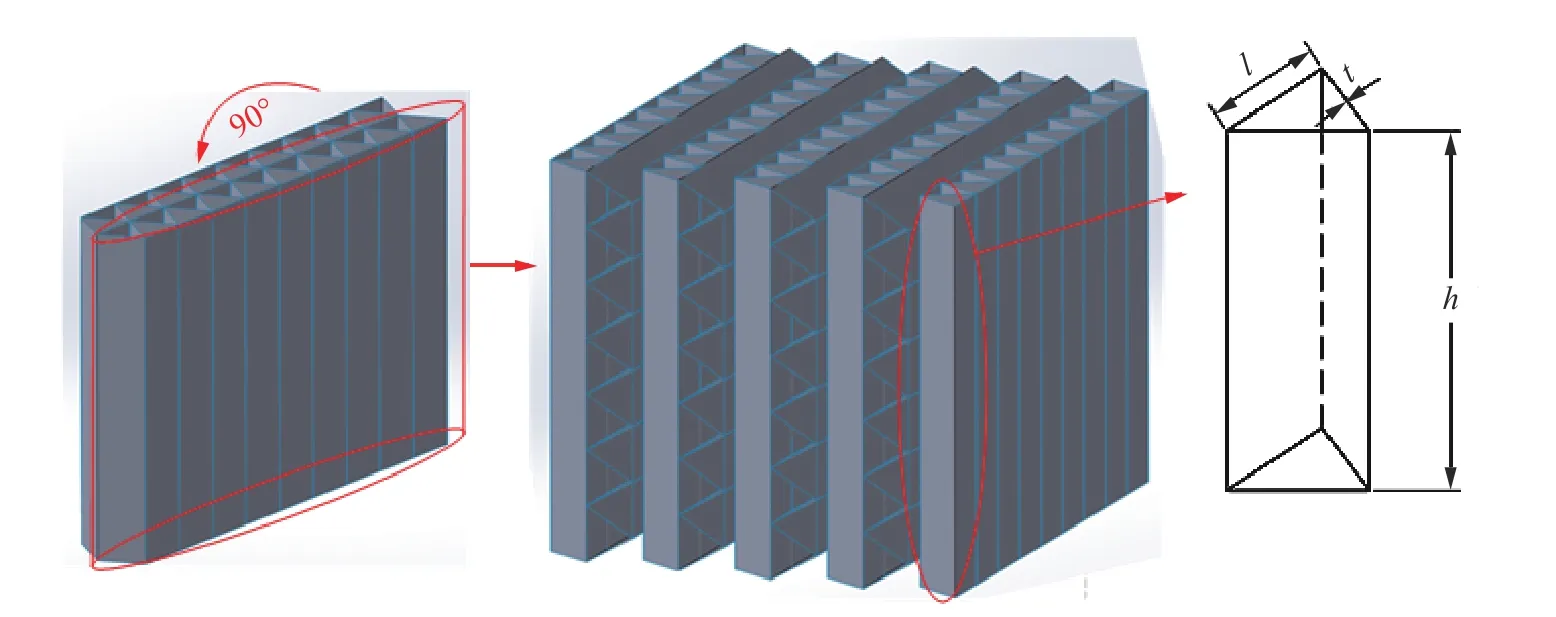
图2 层间组合蜂窝设计思路Fig.2 Design of the staggered honeycomb

1.3 折叠蜂窝

由于传统蜂窝结构的特殊性，导致共面异面承载能力相差甚远。基于此，Zhai 等[19]依据Miura 折纸原理提出了一种共面承载能力优良的折叠蜂窝，通过引入初始折痕对蜂窝进行折叠设计以改变传统蜂窝结构的缓冲特性，控制蜂窝结构的变形模式，但前期并未进行共面和异面承载能力的对比。根据折纸原理，将蜂窝结构沿面内假设为展开后的平面，沿脊线向内、谷线向外折叠，折叠后有两个折叠角α 和γ（α为蜂窝侧面中两条棱之间的夹角，γ 为蜂窝棱边与水平线的夹角）。六边形胞元边长为l，壁厚为t，模型的整体高度为h，设计过程如图3所示。

图3 折叠蜂窝设计思路Fig.3 Design of the folded honeycomb

2 不同构型蜂窝动态压缩有限元模型建立及仿真分析

为了验证建立的高共面/异面新型蜂窝有限元模型的有效性，本文将首先通过对常规的六边形蜂窝进行仿真分析和压缩试验，通过仿真与试验的对比以验证建模和仿真方法的正确性，然后在此基础之上，利用相同的建模方法，建立了新构型蜂窝的共面及异面动态压缩的仿真模型以进行后续的抗冲击性能评估。

2.1 铝蜂窝建模及仿真方法验证

本次试验用3003铝蜂窝采用波纹法制作，胞元短边长c=6 mm，长边长l=10.4 mm，扩展角α =120°，壁厚t=0.045 mm，相对密度为0.006，试验所用蜂窝试样为长宽为77 mm，高为36 mm 的长方体试件，如图4所示。本次试验在TA ElectroForce 3300试验机上进行，试验过程中分别用力传感器和线性位移传感器测量压力和试件位移。在10 s−1应变率下进行了蜂窝异面及共面压缩试验，如图4(c)所示。根据试验机压头的力和位移传感器采集得到的载荷位移曲线，根据σ =F/A,ε =d/H，（其中F为压力，A为蜂窝试件垂直压缩方向的横截面积，d是压头位移，H为蜂窝试件高度）转化得到应力应变曲线。

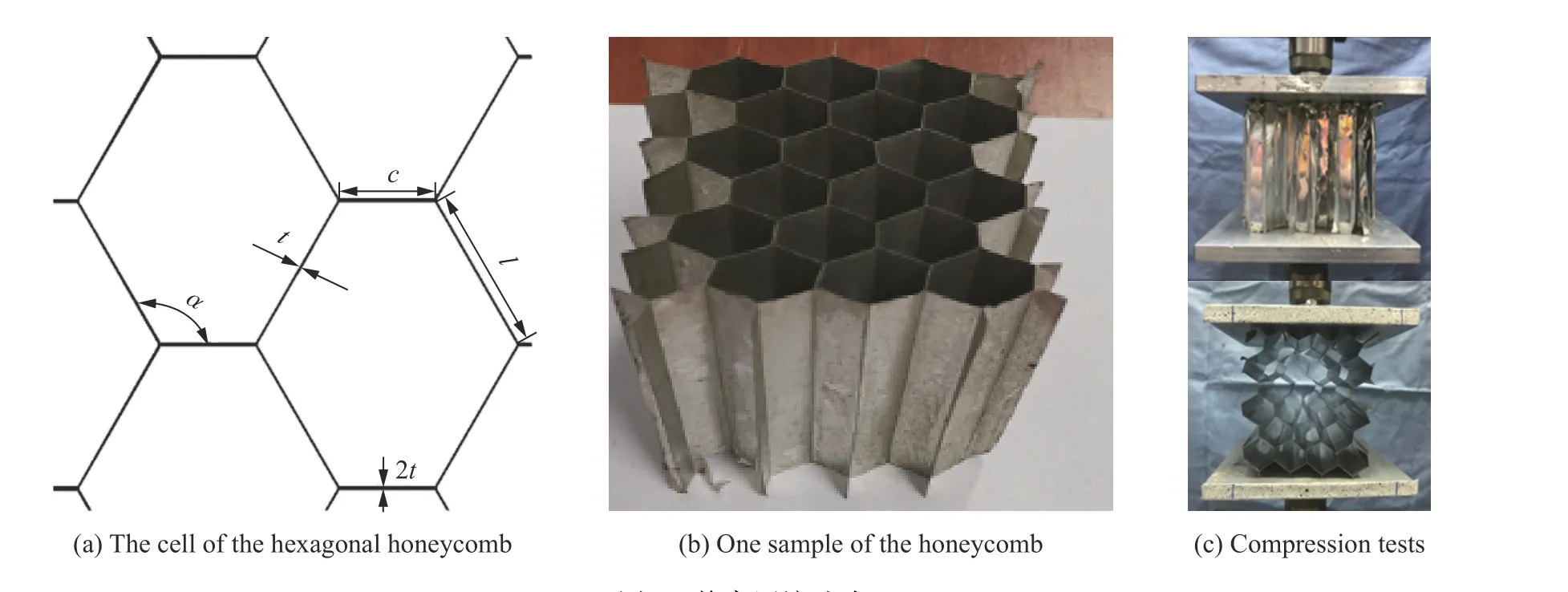
图4 蜂窝压缩试验Fig.4 Compression testson honeycombs

基于HyperMesh 和LS-DYNA 平台建立铝蜂窝异面及共面的动态压缩模型。其中铝蜂窝介于上下两块刚性平板中间，下刚性板施加全固定约束，上刚性板只有压缩方向1个移动自由度。对上刚性板施加强制位移使其匀速冲击蜂窝。另外，两端刚性板与蜂窝之间设置为自动面-面接触，蜂窝自身设置为自接触以模拟铝蜂窝自身之间的接触，设置铝蜂窝自接触摩擦系数为0.1，铝蜂窝与刚性板间的摩擦系数为0.3。

两端刚性墙采用刚性材料（MAT_20）模拟。蜂窝采用多段线性弹塑性模型（MAT_24）进行模拟，材料参数由3003铝蜂窝的基体材料试验得出，弹性模量为70 GPa，密度为2 700 kg/m3，泊松比为0.35，屈服应力为200 MPa。模型采用四节点四边形壳单元进行网格划分，经过网格收敛性性分析，网格大小选择为0.3 mm，厚度方向设置5 个积分点。

为了确定蜂窝有限元模型的有效性，利用上述仿真建模方法，建立了与试验对应的有限元模型，进行仿真模型的验证。由于试验过程中未采用高速摄像机，缺少试验过程照片。对于该模型，仅进行了应力应变曲线的对比。其中10 s−1应变率冲击工况下的异面及共面的仿真与试验所得到的应力-应变曲线对比分别如图5(a)和图5(b)所示。可以看出，异面和共面压缩时试验和仿真的应力应变曲线基本保持一致，平台应力与试验数值接近，表明该模型具有较好的精度。

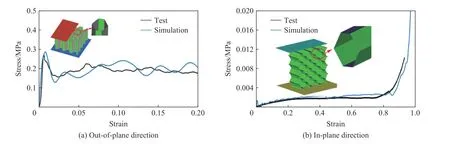
图5 仿真结果试验验证Fig.5 Comparison of the compressivestress-strain curves between test and simulation

为了进一步验证变形模式，参考文献[20]中10 m/s压缩速度的蜂窝异面压缩工况，按照文献中给出的蜂窝尺寸和材料参数进行了仿真分析，应力应变曲线及仿真过程对比分别如图6(a)和图6(b)所示，仿真与试验过程均表现出蜂窝从冲击端对侧发生规则的褶皱变形致使模型逐步压溃，而且平台应力吻合结果较好，进一步验证了该模型的精度。

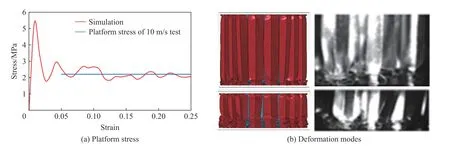
图6 在10 m/s 速度下试验和仿真的对比Fig.6 Comparison of the platform stressand deformation model between test and simulation at 10 m/s

2.2 新构型蜂窝仿真模型建立

表1 不同构型蜂窝的尺寸Table 1 The sizesof different honeycombs

2.2.1胞壁弓字形弯折蜂窝仿真模型建立

按照2.1节经过验证的仿真建模方法，建立了胞壁弓字形弯折蜂窝的有限元模型如图7所示。

图7 胞壁弓字形折叠蜂窝仿真模型Fig.7 The finite element model of the bow-shaped honeycomb

胞壁弓字形弯折蜂窝异面动态压缩的变形过程如图8所示。从图8可以看出，异面沿z轴方向压缩时，压缩过程明显两段化，类似于具有交叉分层梯度特性的串联式组合蜂窝，模型由折叠胞壁相互接触形成的三角形蜂窝和初始六边形蜂窝两部分交叉分布构成，而不是单纯按照梯度进行排列的。从变形过程来看，两部分中六边形蜂窝的承载能力较低，因此首先发生六边形胞壁部分（如图8(a)中红色椭圆区内所示）承受较高应力，从下至上依此发生周期性的折叠变形，表现在图9应力应变曲线中的第1个平台段。当前序蜂窝也就是六边形蜂窝部分压缩密实之后，内部三角形蜂窝才会发生周期性折叠变形使模型进一步坍塌，如图8(b)中黄色矩形区内所示，此时结构的承载能力迅速提高，表现在图9中异面压缩应力应变曲线的第2 个平台段。在异面压缩下，每一部分均出现弹性、塑性坍塌以及密实化3 个阶段。

图8 胞壁弓字形弯折蜂窝异面变形过程Fig.8 The deformation mode of the bow-shaped honeycomb under crush in out-of-planedirection

胞壁弓字形弯折蜂窝承受x和y两个方向的共面动态压缩时，上下刚性板附近的胞壁承受局部高应力，表现为从冲击段对侧产生局部变形带，依次变形压溃，如图10所示。与传统六边形蜂窝相比，由于内部弓字形弯折胞壁相互接触起到重要的支撑作用，改变了初始六边形蜂窝的共面变形模式，胞壁不能直接绕其端点转动而引起胞孔坍塌，此时的主要承载结构由外部胞壁变成内部相接触的折叠胞壁部分，承载方式转化为内部三角形蜂窝承受共面压缩以及折叠胞壁部分的相互接触压溃的耦合承载，大大增加了共面方向的承载能力，由于相邻层的折叠胞壁压溃时间不一致，压溃过程中表现出明显的平台段，最后伴随整个模型压溃进入密实段，承载力急剧上升。由图9可以看出，胞壁弓字形弯折蜂窝在x和y两个共面方向上的承载能力基本一致，且跟异面方向上的承载能力在前期已经比较接近。

图9 胞壁弓字形弯折蜂窝应力应变曲线Fig.9 The stress-strain curves of the bow-shaped honeycomb in in-plane and out-of-planedirections

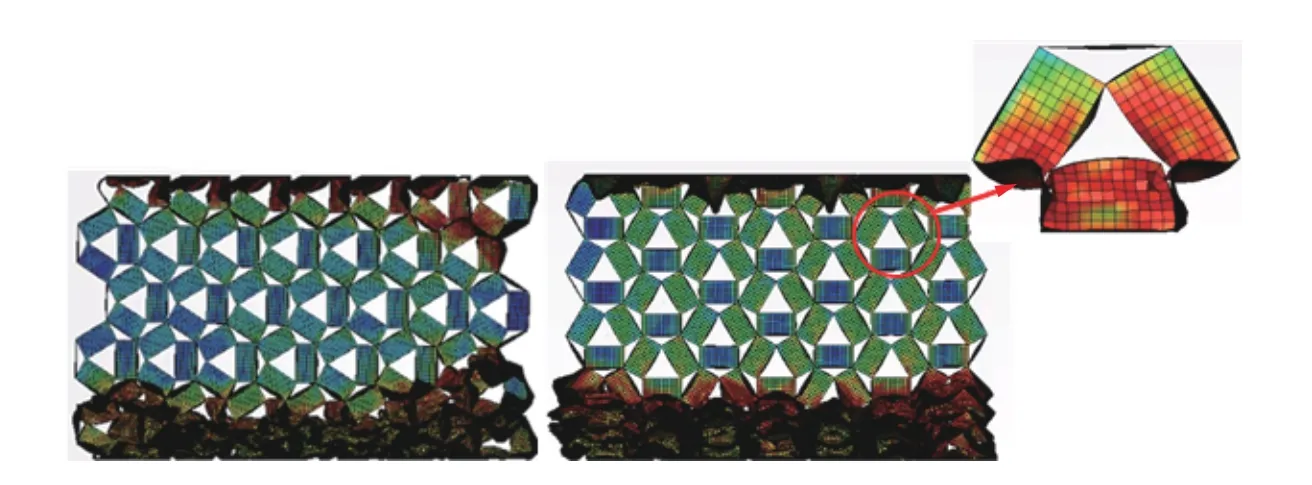
图10 胞壁弓字形弯折蜂窝共面变形过程Fig.10 The deformation mode of the bow-shaped honeycomb under crush in in-plane direction

2.2.2层间组合蜂窝仿真模型建立

按照2.1节中的建模方法，建立了层间组合蜂窝的有限元模型，如图11所示。

图11 层间组合蜂窝仿真模型Fig.11 The finite element model of the staggered honeycomb

由于层间组合蜂窝的设计特点，异面z方向和共面x方向的承载结构一致，因此两个方向上的变形模式趋同，如图12所示。从图12可以看出，此时层间组合蜂窝变形分为两大部分：一部分为平行压缩方向的胞壁，另外一部分为垂直压缩方向的胞壁。其中与压缩方向平行的胞壁等同于传统三角形蜂窝进行异面压缩，变形模式相同，均形成规则的褶皱变形以吸收能量，如图12中蓝色椭圆部分所示，该部分承载能力稳定，是层间组合蜂窝承受异面压缩时的主要吸能部分，形成如图13中应力应变曲线异面承载时的平台段；垂直压缩方向的胞壁在承受压缩时，变形模式类似于传统三角形蜂窝的面内压缩变形，受载后胞壁绕端点转动进而发生弯曲导致模型迅速压溃，如图12中绿色椭圆部分所示，与第一部分相比，该部分吸能能力较弱，对应力的贡献很小。由图13可以看出，由于承载结构的一致性，层间组合蜂窝承受异面压缩和共面x方向压缩时的承载差距很小。

图12 层间组合蜂窝异面和共面x 方向变形模式Fig. 12 The deformation mode of the staggered honeycomb in in-plane direction (x axis direction)and out-of-plane direction

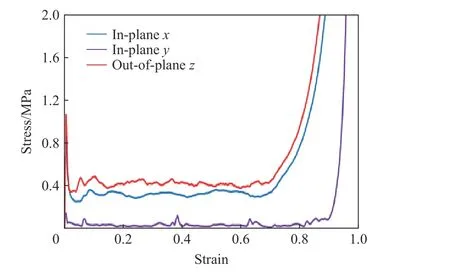
图13 层间组合蜂窝应力应变曲线Fig.13 The stress-strain curves of the staggered honeycomb in in-plane and out-of-planedirections

层间组合蜂窝在承受共面y方向的加载时，此时该构型蜂窝类似于两层传统三角形蜂窝的空间上的交叉组合，每层的变形模式与传统三角形蜂窝共面压缩保持一致，层间组合蜂窝从加载段对立侧开始依次变形，三角形蜂窝的倾斜胞壁发生弯曲导致模型快速压溃，胞孔从上下两端向中间逐渐压垮密实，形成明确的局部化变形带，如图14所示。由于每层变形时间不一致，应力维持稳定上下波动，在该方向上承载能力较差，如图13所示。

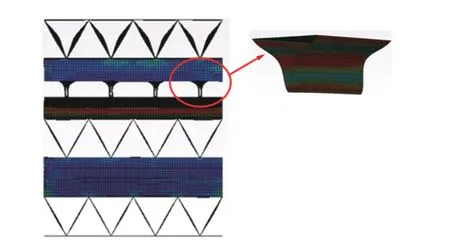
图14 层间组合蜂窝共面y 方向变形模式Fig.14 The deformation modeof the staggered honeycomb in in-plane(y-axis)direction

2.2.3折叠蜂窝仿真模型建立

按照2.1节中的建模方法，建立了压缩下折叠蜂窝的有限元模型，如图15所示。

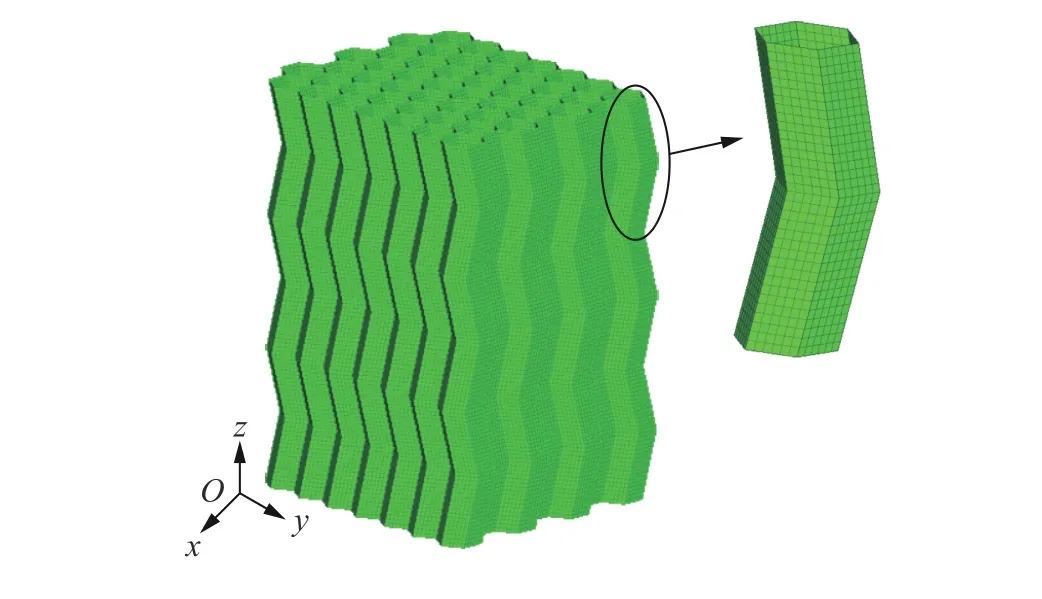
图15 折叠蜂窝有限元模型Fig.15 The finiteelement model of the folded honeycomb

折叠蜂窝受异面z方向的动态压缩变形模式如图16所示。从图16可以看出，由于初始折痕变形的引入，折叠蜂窝的变形模式与传统六边形蜂窝相比发生了变化，异面压缩时，不再形成规则的褶皱变形使模型逐步的稳定压溃，而是变成谷线折叠处向外弯曲变形，脊线折叠处向内弯曲变形，模型主要依赖Miura 机制进行折叠。因为初始折痕的引入，导致耗能水平下降，该构型的异面承载能力得到一定的削弱，相较传统六边形蜂窝有所下降。

图16 折叠蜂窝异面压缩变形模式Fig.16 The deformation modeof the folded honeycomb under crush in out-of-plane direction

共面压缩时，x方向加载时，出现分层变形模式，塑性区域主要出现在胞壁交接线上。开始承载时刻胞壁绕其端点转动形成塑性铰而使模型初步压溃，在该过程中模型在中部形成局部变形带，从两侧向中间逐层压溃，如图17(a)所示。胞壁并未发生大面积的塑性变形即进入初始压密状态，载荷保持稳定的同时稍有提升。随着初始密实段的完成，从另一角度来看，由于折叠蜂窝具有初始折叠角，因此在x方向承载时需克服折叠角而使模型逐渐压平，此时承载力提升速度加快，模型承载能力进一步提高，伴随着胞壁的相互接触，模型进入最终密实化阶段，变形过程如图17(b)所示。在达到初始峰值应力后，常规蜂窝上的应力一般迅速减小，随后出现一些波峰和波谷维持在平台段。但是，折叠蜂窝在初始峰值应力点后的应力值仍然较高，结构的平台应力随之增大，吸能能力也随之增大，如图18所示。当进行y方向加载时，初始折痕的引入并未明显改变变形模式，倾斜胞壁形成塑性铰，于模型中部形成明显的局部变形带，整体表现为V 形变形，如图19所示。折叠蜂窝结构的应力变化比传统蜂窝结构的应力变化更平滑，吸能能力明显增强，如图18所示。

图17 折叠蜂窝共面x 压缩变形模式Fig.17 The deformation mode of the folded honeycomb under crush in in-plane (x-axis)direction

图18 折叠蜂窝应力应变曲线Fig.18 The stress-strain curves of the folded honeycomb in in-planeand out-of-plane directions

图19 折叠蜂窝共面y 压缩变形模式Fig.19 Thedeformation mode of the folded honeycomb under crush in-plane (y-axis)direction

3 新构型蜂窝抗冲击承载吸能评价

蜂窝结构的承载能力与变形模式、屈曲变形区平台应力以及能量吸收率密切相关。在相对密度及冲击工况保持一致的前提下，利用不同评价指标进行胞壁弓字形弯折蜂窝、层间组合蜂窝和折叠蜂窝3种新构型蜂窝的抗冲击承载能力分析。此外，为了与传统六边形蜂窝的抗冲击承载能力进行对比，本文同时也进行了相同冲击工况下的相对密度一致的六边形蜂窝的动态压缩仿真，此时六边形蜂窝模型的质量和体积 别为1 .291g 和22 869 m m3。

3.1 蜂窝吸能评价指标

蜂窝由于结构的特殊性，压溃过程中，主要通过平台段（对应于图20中δs到δe段）蜂窝胞壁变形坍塌吸收能量，平台应力通常用来表征蜂窝的吸能能力。首先计算出平台力Fp，然后将平台力转化为平台应力σp：

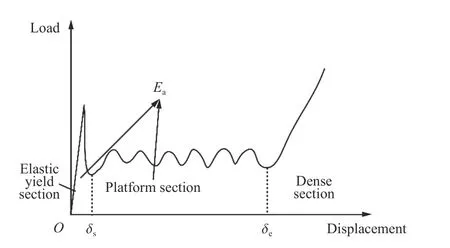
图20 铝蜂窝压缩特性曲线Fig.20 The compression curveof an aluminum honeycomb

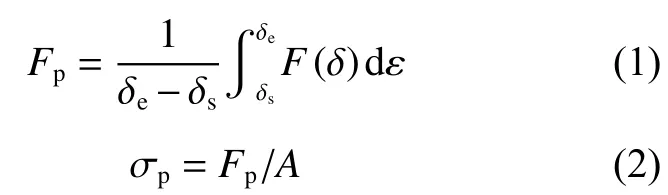
式中：σp为平台应力， δs和δe分别为平台段开始时和结束时的位移。

定义K为蜂窝在共面/异面平台应力的比值：

式中：σi为共面压缩平台应力，σo为异面压缩平台应力。K值越大，说明蜂窝的共面、异面平台应力越接近。

质量比吸能（Ea,s）是评价蜂窝材料在受压缩过程中能量吸收能力的重要指标，是缓冲吸能装置设计的重要参数。质量比吸能的计算公式为：

式中：Ea指蜂窝从初始压缩时刻至蜂窝密实化阶段开始时刻为止，蜂窝结构所吸收的能量，对应于图20中弹性屈服段和平台段下载荷位移曲线与位移轴所围成的面积；m表示结构的质量，显然比吸能越大，代表结构吸能能力更好。

本文中定义R为蜂窝共面/异面质量比吸能的比值，来评价共面和异面方向的吸能差异的大小：

式中：Ea,s,i为共面比吸能，Ea,s,o为异面比吸能。显然质量比吸能Ea,s越大，单位质量的蜂窝结构吸能越多，吸能效率越高。R值越大，说明蜂窝共面、异面吸能的效率越接近。

3.2 不同构型蜂窝吸能特性对比

3种新蜂窝构型与传统六边形蜂窝的平台应力对比如图21和表2所示。从对比的结果可看出，3种新型蜂窝均通过削弱异面承载能力的同时提高共面承载能力的方式来缩小异面与共面抗冲击承载能力的差距，K值均高于传统六边形蜂窝。传统六边形蜂窝共面及异面承载的平台应力差距近50多倍。胞壁弓字形弯折蜂窝共面方向承载能力均匀，较传统六边形蜂窝K值，弓字形弯折蜂窝共面方向平均提升21.3倍。折叠蜂窝共面x方向强于y方向，K值平均提升21.3 倍。层间组合蜂窝由于结构的特殊性，两个共面方向承载能力差距大，共面x方向承载结构与异面方向趋同，承载能力提升尤为明显，该方向的K值提升了42倍，平台应力基本与异面方向持平，y方向承载能力偏低，但K值也提升了3.8倍。

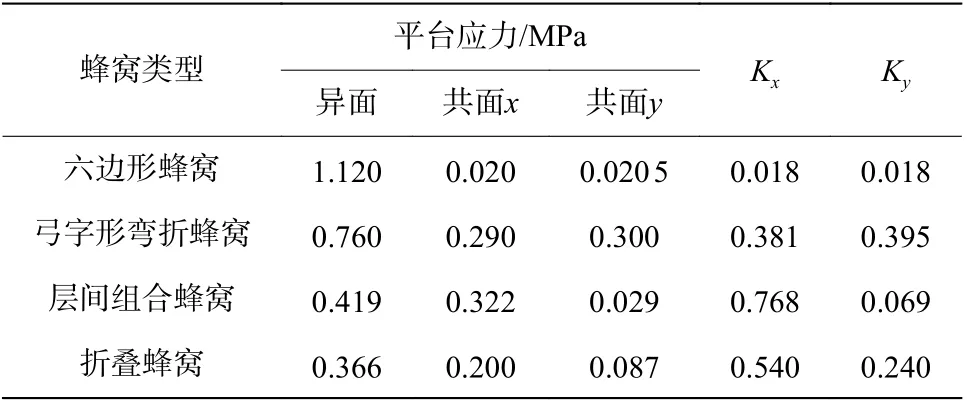
表2 不同构型蜂窝结构的平台应力Table 2 Platform stresses for different honeycombs

图21 平台应力比较Fig.21 Comparison of the platform stress among different honeycombs

3种新构型蜂窝与传统六边形蜂窝的共面及异面的质量比吸能对比如图22和表3所示。可以看出，传统六边形蜂窝在共面方向的质量比吸能远小于异面方向，差距50多倍。从对比的结果可看出，类似于平台应力的比较结果，3种新构型蜂窝较传统六边形蜂窝异面方向上的比吸能得到削弱，共面方向上的比吸能得到加强，共面和异面的承载能力差距也在不断缩小。

表3 不同构型蜂窝结构的质量比吸能Table 3 Specific mass energy absorption for different honeycombs

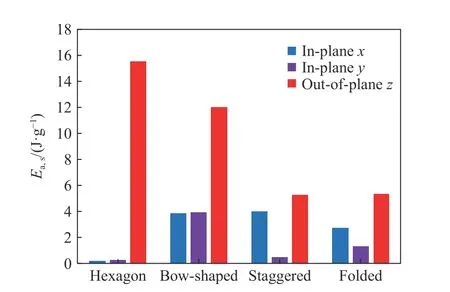
图22 共面与异面质量比吸能对比Fig.22 Comparison of the mass-specific energy absorption of different honeycombs in out-of-plane and in-plane directions

表现在R值上，弓字形弯折蜂窝两个共面承载能力相近，较传统六边形蜂窝平均提升17.2倍，折叠蜂窝共面x方向强于y方向，平均提升20.8倍。层间组合蜂窝的两个共面方向的质量比吸能差距较大，x方向表现突出，R值提升43.3倍，y方向表现欠佳，R值提升4.9倍。

需要说明的是：新构型蜂窝的设计在不同程度提高了共面和异面的承载吸能比，为各向同性蜂窝的设计提供了思路。如果单从异面方向来看，设计的新构型蜂窝与传统蜂窝相比，异面承载能力有所削弱。考虑到目前蜂窝结构的一些实际应用场景，例如汽车的成不同角度的低速碰撞、直升机方向不确定的低空坠毁、城市安全岛防护等场景。往往是碰撞速度低、碰撞方向不确定，此时无需异面方向的高强度，但需要蜂窝抗全向缓冲的特性。此外，异面承载能力的削弱，也可以通过调整蜂窝孔隙比率或者壁厚等参数来弥补，而且目前该种具有小孔隙比的异面高强度蜂窝制作工艺方法已经非常成熟，因此上述设计的3种高共面/异面承载吸能比的新型蜂窝结构，有望能更好地满足工程实际对多向承载的需求。

4 结 论

提出了3种高共面/异面抗冲击承载能力的新构型蜂窝，分别是胞壁弓字形弯折蜂窝、层间组合蜂窝和折叠蜂窝。通过传统六边形蜂窝共面及异面的压缩试验验证了仿真方法的正确性，然后根据该仿真方法建立了新构型蜂窝的共面及异面动态压缩的有限元模型，分析了其变形模式和承载能力。相较相同相对密度下的传统六边形蜂窝，研究发现3种新型蜂窝均提高了共面方向的承载能力，且缩小了共面和异面方向的承载能力差距，提高了共面/异面承载比值。从平台应力指标来看，胞壁弓字形弯折蜂窝两个共面方向承载能力相当，共面/异面承载比相较六边形蜂窝提高21.3倍；层间组合蜂窝由于结构特殊，两个共面方向承载能力悬殊，其中一个共面方向的共面/异面承载比提高42倍，但另一方向仅提高3.8倍；折叠蜂窝共面x方向的承载能力大于y方向，共面/异面承载比提高了21 倍。从质量比吸能结果来看，胞壁弓字型弯折蜂窝、层间组合蜂窝、折叠蜂窝的共面/异面承载比分别提高了17.2倍、20.8倍和43.3倍。今后可以进一步研究上述新型蜂窝的制作工艺，以逐步实现在汽车航空等需要多向承载吸能的场景中的应用，为多向载荷冲击下的蜂窝结构设计提供参考依据。