数学家泰勒斯的成就

季晓春

泰勒斯（Thales，公元前624-546）是古希腊时期的数学家、科学家、哲学家，出生于米利都城，创建了古希腊最早的哲学学派，是希腊最早的哲学学派——米利都学派（也称爱奥尼亚学派）的创始人，泰勒斯几乎涉足了当时人类的全部思想和活动领域，获得崇高的声誉，被尊为“希腊七贤之首”.泰勒斯为人类的自然科学和哲学的发展作出了伟大的贡献.

一、测出金字塔的高度

泰勒斯在埃及时曾测出了金字塔的高度.最早的记载出自海罗尼莫斯（Hieronymus，公元前4-前3世纪），引用他的话说，泰勒斯利用人的身高和影子相等时金字塔的高也和影子相等的道理，成功地测出金字塔的高，普利尼（Pliny，公元23-79年）也有类似的记载：泰勒斯发现在人身和影子等长的时候去量物体的影子，可以得到金字塔或者其他物体的高.普卢塔克（Plutarch，公元46-119）认为是泰勒斯利用了相似三角形的原理.

如果太阳在适当的位置，影长还是可以量出来的.以最大的胡夫金字塔为例，原高146.5米，底为每边长230米的正方形，四面正对着东南西北，如果太阳位于正东、正南、正西（正北是不可能的），仰角又小于侧面与底的夹角∠OMP（约等于51°52'），如图1，塔影就是一个等腰△AQB，影长应该是OQ=OM+ MQ，而OM等于底边长的一半，只要量出MQ就行了，如果应用相似三角形的性质，下一步的工作是计算比例.若避免用比例式，可以在太阳的仰角为45°时（即杆长与影长相等时）再量MQ，这时OQ就是塔高.

比方，每天正午（太阳在正南方）定时观测杆影，不难发现秋分以后影子逐渐增长，到了某一天，影长和杆长相等，这时太阳既在正南，仰角又是45°.若选择正东或正西方向，情况与此类似.总之，只要耐心观察，不通过比例式也能得到测度塔的高，

若允许应用比例式进行计算，就可以不必受时间的限制.较合理的办法是作两次观测.第一次记下杆顶影子的位置a，和塔顶影子的位置A，第二次观测时杆顶影子在6处，塔顶影子在B处，那么，AB：ab就等于塔高与杆长的比.这说明泰勒斯对相似形已有初步的认识.

二、发现有关平面几何学的结论

公元450年，普罗克洛斯（Proclus，公元410-485，希腊哲学家、天文学家、数学家、数学史家1在给欧几里得《几何原本》卷I作评注时，写了一部有关几何学发展的概要，叫做《普罗克洛斯概要》（或叫《欧德莫斯概要》，因为它主要取材于欧德莫斯（Eudemus，约公元前335年）的《几何学史》）.他在《普罗克洛斯概要》中写道：“泰勒斯是将这种学问（几何学）知识从埃及带回希腊的第一人.他发现了许多命题，又将一些重要原理传授给他的追随者，他的方法有些是具有普遍意义的，也有一些是经验之谈，”

普罗克洛斯指出泰勒斯发现的命题有：

1.圆的直径将圆平分.

普罗克洛斯说，泰勒斯是第一个证明了这个命题的，在《几何原本》中，欧几里得也只是将其作为定义提出来（卷I定义17：直径是通过圆心的直线，……将圆平分）.

2.等腰三角形两底角相等.

这是《几何原本》中卷1的命题5，也就是有名的“驴桥”，泰勒斯是用“相似”这个词来描述相等角的，说明他还未将角作为具有大小的量，而是将其看作有某种形状的图形.这和古代埃及人的观点一致.

3.两直线相交，对顶角相等.

这是《几何原本》卷1的命题15.

4.有两角夹一边分别相等的两个三角形全等.

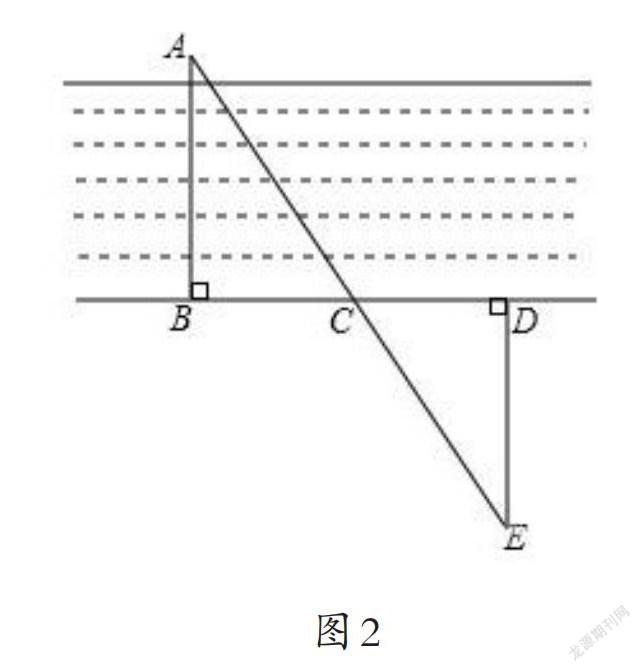
这是《几何原本》卷I的命题26.欧德莫斯在《几何学史》中将这个定理的证明归功于泰勒斯，并说他利用这个定理测出船只到岸边的距离.泰勒斯利用三角形全等的方法求出岸上一点到海中一艘船的距离.如图2，B是观察点，船4在B的正前方，过B作AB的垂线，在垂线上截取任意长BD，C是BD的中点，观察者从点D沿垂直于BD的DE方向走，直到点E、船A和点C在一条直线上，那么△ABC≌△EDC，从而量出DE的距离即为船离岸的距离AB.

5.半圆所对的圆周角是直角.

这是第欧根尼的记载，他引用潘菲拉（Pamphila）的话说，泰勒斯从埃及人那里学到了几何学，第一次在圆内作内接直角三角形，并为此宰了一头牛来庆祝.

如果这记载可靠，那么泰勒斯的几何学知识已经达到相当高的水平，而且还掌握了更多的知识，如三角形内角和等于两个直角、在圆的直径上的内接三角形一定是直角三角形.

最有名的是以他的名字命名的定理——泰勒斯定理.泰勒斯定理：若A，B，C是圆形上的三点，且AC是直径，∠ABC必然为直角，如图3所示.该定理在欧几里得《几何原本》第三卷中被提到并证明.

泰勒斯定理的逆定理同样成立，即：在直角三角形中，直角的顶点在以斜边为直径的圆上，该定理是平面几何中的一个重要定理.它也被归功于希腊数学家泰勒斯.

三、引入了命题证明的思想

上述的结论看起来并不复杂，有些仅凭直观判断就能得出，然而泰勒斯不满足于“知其然”，还要穷究“所以然”.他把它们整理成一般性的命题，论证了它们的严格性，并在实践中广泛应用.

泰勒斯在数学方面的划时代的贡献是开始引入了命题证明的思想.在数学中引人证明的思想，这是难能可贵的，从此数学从具體的、实验的阶段过渡到抽象的、理论的阶段，逐渐形成一门独立的、演绎的科学.

命题的证明，就是借助一些公理或真实性已经被确定的命题来论证某一命题的真实性的思想过程.它标志着人们对客观事物的认识从经验上升到理论，这在数学史上是一次不寻常的飞跃.

证明命题是希腊几何学的基本精神，而泰勒斯是希腊几何学的先驱.

泰勒斯是公认的希腊哲学鼻祖，他第一次冲破了超自然的鬼神思想的羁绊，去揭示大自然的本来面目，他断言水是万物的本质;而地球像一个圆盘，漂浮在浩瀚无垠的水中，欧德莫斯说他已知按春分、夏至、秋分、冬至来划分的四季是不等长的.

泰勒斯思想的影响是巨大的.在他的带动下，人们摆脱了神明思想的束缚，去探索宇宙的奥秘，经过数百年的努力，出现了希腊科学的繁荣，泰勒斯的首创之功，不可磨灭.