中国股市非流动性对市场超额收益的预测研究

谢军，胡楠，高斌，罗恬恬

摘要：从非流动性的内涵出发，计算沪深300指数的七个非流动性指标，并通过主成分分析法对七个非流动性测度进行降维，获得市场综合非流动性指标。使用ARFIMA模型拟合各变量的长记忆性及残差相关性，构建蒙特卡洛模拟衡量因长记忆性及残差相关性对预测回归的影响程度，使用Bootstrap抽样法调整偏差及筛选具有稳健预测能力的非流动性测度。结果表明：非流动性测度能够对超额收益进行短、中及长期预测，prin和fht指标有较高的预测拟合优度，非流动性因子是因子定价理论的重要因子，且大多非流动性指标对市场超额收益的短期预测能力来源于市场波动，而中长期预测能力由与波动无关的非流动性因素主导。

关键词：非流动性;长记忆性;流动性溢价;市场波动

文章编号：2095-5960（2021）02-0031-10;中图分类号：F830;文献标识码：A

一、引言

流动性是一个广泛而复杂的概念，具有多个不同的侧面，是反映资本市场运行状况的关键因素，与资产收益的关系密不可分。换手率是常见的流动性测度之一，张峥和刘力使用横截面数据，以换手率测度流动性，分析其与股票收益的关系，结果表明两者呈负相关，换手率较低的股票具有更高的预期收益。[1]在流动性的研究中，流动性的对立概念/非流动性（illiquidity）也被诸多学者用于流动性测度及预期收益预测。Tirole对非流动性的概念进行了梳理，顾名思义，非流动性就是指资本市场中参与者买入或卖出某项资产所面临的阻碍，市场的非流动性越高，资产的流动性就越低，到一定程度时，将会触发市场冻结、资产甩卖、危机蔓延甚至公司最终破产和政府救助。[2]

诸多学者从不同方面对非流动性进行测度，Roll使用股票相邻两天的收益协方差衡量相对有效价差[3]，Corwin & Schultz则使用最高报价与最低报价衡量股票的价差，从价差方面定义非流动性指标，价差越高非流动性程度越高，市场流动性越差[4];不限于价差，Pástor & Stambaugh从收益率逆转出发，根据收益率对订单流的逆转程度以衡量股票的非流动性;[5]Hou & Moskowitz基于股票对市场消息的反应速度测度非流动性，使用个股收益率拟合不同时段的市场收益率，通过拟合优度的比值表示非流动性程度; [6]Fong， Holden & Trzcinka结合市场波动因素得到市场波动及边际交易成本的非流动性测度; [7]根据Kyle对非流动性的定义，给定交易量对股价影响越大意味着其流动性越差;[8]Amihud以日度收益及日度交易金额得到计算得1元交易量所对应的价格变化幅度，其数值越大则非流动性程度越高。[9] 上述指标从五个方面测度非流动性，对非流动性的定义进行了较为综合地诠释。

高度非流动性与市场萧条、金融危机伴随出现，这使得非流动性指标预测市场超额收益成为可能。Chen等人使用非流动性指标预测标普收益率及宏观经济指标。 [10]Chen等人发现Amihud非流动性指标对经济衰退开始时点具有很强的预测能力。[11]而国内学者对于非流动性指标多集中于Amihud指标，其他非流动性测度及其预测研究涉足较少。王春峰和韩冬最早在我国股市应用Amihud非流动性测度，检验市场非流动性与股票收益关系。[12]闫东鹏和吴贵生基于Amihud非流动性指标，构建其变体对股票回报进行预测。[13]黄峰和杨朝军分析Amihud测度与股价关系，发现我国股市存在对非流动性水平的收益补偿，符合流动性溢价理论预期。[14]这一点也在谢赤等人的研究中得到了论证。[15]

但是，上述研究存在三个方面的缺失。第一，从资本资产定价模型到套利定价理论，多因子定价理论得到极大发展，如Fama-French三因子、五因子研究[16，17]。但是学者对非流动性因子尤其是综合非流动性因子的研究涉足较少。因此，本文提出假设：非流动性因子是因子定价理论的重要因子。具体的，通过主成分分析法对多个方面非流动性测度降维，获得综合性非流动性因子，并分别使用样本内及样本外方法，以非流动性因子预测超额收益率，根据其预测结果验证上述假设，丰富因子定价领域研究。第二，当前的预测研究多未考虑长记忆性对预测斜率的影响，对流动性溢价的论证不够严谨。本文进行模型偏差研究以获得偏差调整斜率，既能更严谨地论证流动性溢价理论，又能将准确的斜率应用于样本外实战。具体的，应用ARFIMA模型拟合非流动性指标及超额收益率的长记忆性参数，分析非流动性指标及超额收益率的残差相关性，通过构建蒙特卡洛以评估长记忆性及残差相关性造成有偏预测程度，并根据蒙特卡洛的结果对非流动性指标采用Bootstrap偏差纠正及检验。第三，鉴于中国股市的弱有效性，收益率对流动性信息反应速度可能较慢，非流动性的预测能力可能在中长期而非短期，而当前关于流动性因子的多期预测研究甚少，因此本文将上述8个非流动性指标对沪深300指数超额收益率进行短、中及长期预测;最后，本文剔除非流动性指标的市场波动因素，通过分解非流动性因子剖析其预测能力来源，并论证了非流动性因子的稳健预测能力。

二、指标体系构建

（一）非流动性指标

价格影响测度AMIHUD：由Amihud提出 [9]，根据股票日度收益及交易金额得到，即1元交易量所对應的价格变化幅度，体现了每单位交易量对价格的影响，具体计算公式如下：

AMIi，t=1Di×∑Did=1|Ri，d|RVOLi，d（1）

其中，Di指第i家公司在该月的有效交易天数。|Ri，d| 指第i家公司日收益率的绝对值，RVOLi，d指对应的人民币日度交易量。考虑到通货膨胀的影响，本文用CPI环比增速对AMI指标进行调整。

有效价差测度CS：参考Corwins & Schultz的方法构建指标[4]，使用每日数据中的最高报价和最低报价来估算买卖价差，代表股票日度最高（低）价与股票真实价值最高（低）值的差值，差值越大表示股票的非流动性程度越高。

边际交易成本及波动测度FHT：该指标反映了市场交易成本中的收益波动和边际交易成本，由Fong等人提出[7]。具体计算公式如下：

FHTt=In（2）+volt+g（ZEROSi，t）（2）

信息时滞测度HM：根据个股收益对当期及过去市场收益的反应程度比例获得，由Hou和Moskowitz提出[6]。具体的，使用拟合优度表示个股收益对当期或过去市场收益的反应程度。具体计算公式如下：

RETi，d=αi+βiRETm，d+∑5n=1δniRETm，d-n+εi，d（3）

其中RETm，d为第d交易日市场收益率，RETi，d指第d交易日个股收益率，RETm，d-n指第（d-n）交易日市场收益率。取滞后系数δi为0得拟合优度R2（restricted），滞后系数δi不为0得拟合优度R2（unrestricted），分别反映个股收益对当期市场收益的反应程度、对当期及过去市场收益的反应程度。若股票的信息反应速度快，则个股收益对当期市场收益的反应程度R2（restricted）高，非流动性测度HM低。

HM=1-R2（restricted）R2（unrestricted）（4）

收益逆转测度PS：Pástor & Stambaugh提出的流动性指标 [5]，通过收益率逆转程度以衡量流动性。如果股票不是完全流动的，那么人们对股票收益的预期将会发生逆转，而这种预期反转越大，股票的流动性就越低，即与订单流相关的收益变化是流动性效应的结果。

RETei，d+1=θi+φiRETi，d+γisign（RETei，d+1）RVOLi，d+εi，d+1（5）

其中，RETei，d+1指股票i第（d+1）交易日的个股超额收益率。RETi，d指股票i第d交易日的超额收益率，RVOLi，d指第d交易日的人民币交易量。将PS指标乘以一个负数获得最终的PS非流动性指标，日度PS指标加总平均获得月度测度。

有效价差测度ROLL：由Roll提出的有效价差估计值。[2]与CS指标不同，ROLL指标由股票收益率的协方差得到。若ROLL≥0时，则不再符合假设预期，取ROLL为0。

边际交易成本测度ZEROS：为零收益天数占交易天数的比例，即每月零收益天数除以交易天数，获得月度ZEROS指标。考虑到股票停牌的情况，因此本文选取的零收益天数只包括股票交易量为正的交易日。[18]

（二）综合非流动性测度构建

鉴于各非流动性指标代表流动性的不同侧面，因此以主成分分析法对非流动性指标进行降维，获得综合性的非流动性测度。以主成分分析法对非流动性指标进行加权平均降维获得综合非流动性指标，取第一主成分作为综合测度。

print=k1amit+k2cst+k3fhtt+k4hmt+k5pst+k6rollt+k7zerost（6）

其中print为主成分分析法所得综合非流动性指标，ki是非流动性指标在第一主成分的对应系数。

（三）超额收益和波动率指标

本文将沪深300指数的市场超额收益率作为预测目标，由沪深300指数的对数收益率减去无风险收益率得到，记为y。市场波动率为沪深300成分股收益率标准差在相应时间间隔中的横截面平均值。

voli，j=di，jσ（reti，d，j）（7）

其中voli，j为第i月第j家公司的市场波动率，reti，d，j为第j家公司第i月第d天的股票收益率，σ（reti，d，j）为第j家公司第i月日度股票收益率的标准差，di，j表示第i月第j家公司股票的有效交易天数。从统计学的角度考虑，对所有指标都进行对数转换，小写字母即表示经过对数处理的变量，如ami=In（AMI）。

三、数据与模型

（一）数据和描述性统计

本文数据主要来源于锐思数据库，选取了2005年4月至2019年3月期间沪深300成分股，通过等额加权平均日度非流动性指标获得月度因子。表1展示了非流动性指标以及其他变量的描述性统计，面板A为各变量的均值、标准差、偏度以及斜度。面板B展示了各变量之间的相关性，可以发现cs、hm、ps以及roll指标与同期超额收益呈正相关，即流动性越差，同期股票收益越高。而ami、fht、zeros以及prin指标相反。图1以fht， zeros和prin因子为例（为防止曲线过多造成图形杂乱），刻画了非流动性指标走势。在2008年经济危机及2015年股灾前夕，市场流动性枯竭，非流动性指标大幅上升;形成鲜明对比的是，在2007年及2015年上半年股市大涨前夕，市场流动性充裕，非流动性指标急剧下降，契合股市实际周期。

（二）变量长记忆性和残差相关

Stambuagh指出变量过高的记忆性会导致预测回归中的计量问题，尤其是预测因子和目标之间存在残差相关性时，估计所得斜率是有偏的。 [19]长记忆性指变量的自相关衰减速度较慢，通常以双曲线速率衰减。相对地，短记忆性时间序列自相关性以指数速率衰减，远远快于长记忆性变量。本文对各变量进行1、12以及36阶自相关性分析，比較其衰减速度。并且利用ARFIMA模型对平稳的长记忆时间序列进行建模，以拟合各变量的具体长记忆性参数d。ARFIMA模型是差分单整移动平均自回归模型（ARIMA）的拓展，其允许ARIMA模型进行分数差分。通过对非流动性指标以及其他指标进行长记忆参数拟合，本文发现大多非流动性指标、超额收益指标以及市场波动指标的d值都不为0，存在长记忆性。鉴于这些指标也存在一定的短记忆性，对非流动性指标、超额收益指标以及市场波动指标都应用ARFIMA模型，其中AR模型体现了指标的短记忆性，而d值体现指标的长记忆性。该过程可以写成：

2（L）（1-L）d2（yt-μx）=θ2（L）ε2，t

εt≡（εx，t，εy，t）′～iidN（0，Σ）

（1-L）d=∑∞s=0Γ（s-d）Γ（-d）Γ（s+1）Ls（8）

其中，x（z）=1-x，1z-…-x，pxzpx，θx（z）=1+θx，1z+…+θx，qzq为多项滞后算子。（1-L）d为由二项展开式定义的分数差分算子，Γ（·）代表伽马函数。残差εt=（ε1，t，ε2，t）′～iidN（0，Σ），Σ为一个正定对称矩阵，残差同期相关系数ρ=Σ12/Σ11Σ22。

通过式的ARFIMA模型完成滤波得超额收益率残差值ε1，t及非流动性指标残差值ε2，t，通过对两者进行相关性分析得残差相关性结果。表2面板A呈现了各变量的1、12及36阶自相关系数以及长记忆性参数d，与预期结果一致：变量长记忆性参数d越大，其自相关系数衰减速度越慢。具体的，价格影响测度ami及综合非流动性测度prin的长记忆性系数都接近于0，其自相关系数衰减速度极快;相反的，长记忆性参数较高的fht测度及zeros测度自相关系数衰减极慢。面板B展示了非流动性指标与超额收益率的残差相关性，ami指标、cs指标以及roll指标与超额收益率具有显著的残差相关性。但是，仅根据表2无法分析得多大程度的长记忆性及残差相关会对预测斜率造成干扰，因此构建蒙特卡洛模拟进一步分析。

（三）蒙特卡洛模拟

為了更严谨地评估变量长记忆性以及残差相关性对回归的影响程度，本文构建蒙特卡洛分析。首先，随机生成两组相关系数为ρ的时间序列，记为εx，t和εy，t。ρ的取值范围为-08到08，通过对两者相关系数ρ的不同取值，赋予εx，t、εy，t序列具有不同程度的相关性;其次，对两组随机时间序列应用ARFIMA（p，d，q） 模型，参数d取值范围为01到09;最终，得到了具有不同长记忆性和残差相关性的两组时间序列x及y，重复运算2500次获得蒙特卡洛结果。鉴于超额收益率存在一定程度的自相关性，应用AR（p） 模型以使蒙特卡洛模拟更加契合变量的特征，得到蒙特卡洛的预测模型：

yt=α+β1∑Jj=1yt-j+βxt-1+νt（9）

表3呈现了蒙特卡洛结果，面板A为根据上式所得的β值，即长记忆和残差相关系数的变化对预测造成的影响。可以发现，当残差相关系数ρ=0时，β基本等于0，而当ρ发生变化时，β随之变化，表明残差相关性的存在造成了“Stambaugh”偏差[19];残差相关系数ρ不变时，偏差随长记忆参数d递增。面板B展示了长记忆性及残差相关性造成偏差对回归显著性影响。结果表明：当ρ≠0时，斜率β就会产生明显误差，并且长记忆性参数d的变化也会对β造成影响。

（四）偏差纠正

通过蒙特卡洛模拟分析，可以发现长记忆性和偏差同期相关对β值和回归结果显著性存在干扰，从而造成不准确的预测结果。而根据表2的结果，几乎所有非流动性指标都有长记忆性及残差相关性。为了纠正变量长记忆性以及偏差同期相关造成的斜率误差及筛选出受误差干扰较小的测度，本节应用Bootstrap抽样法，具体过程如下：首先应用ARFIMA模型得到时间序列的残差值εt ≡（εx，t ，εy ，t ），剔除同期相关以外的数据特征。其次，对残差进行401次抽样生成样本，拟合ARFIMA模型得到参数p和q，进行分数差分获得样本（x*t，y*t）′，该样本只具有残差相关及长记忆数据特征。最后，对x*t和y*t应用式所示预测模型，记录回归所得的β^*，即因长记忆性及残差相关性造成的偏差斜率。重复上述抽样过程2500次得到2500个的偏差斜率β^*i ，取均值得到最终偏差斜率。将最小二乘法所得斜率减去偏差斜率，得到修正后的斜率，并计算Bootstrap抽样拒绝比以检验非流动性指标稳健预测能力。

β^*=β^-12500∑2500i=1β^*i（10）

其中β^为最小二乘法所得斜率，β^*i为第i次抽样所得斜率，K为β^*i>β^的次数。

四、非流动性指标预测能力分析

（一）样本内预测能力分析

鉴于股票收益变化常常会滞后于市场流动性的变动，有必要使用非流动性指标进行短、中及长期预测。因此，本节使用了全样本数据进行单月、一季度、半年及一年期样本内预测，考虑到被解释变量具有较高的自相关性，对超额收益变量应用了AR（p）模型，预测模型如下：

yt=α+β1∑Jj=1yt-j+βxt-l+νt（11）

其中，l分别取1、3、6和12，即利用非流动性指标预测未来一个月（一期）、一季度、半年以及一年后股票超额收益，j取1对应AR（1）模型。经过回归后得到了初始β值，同时经过Bootstrap获得修正后的斜率。

表4展示了非流动性指标对股票超额收益的样本内预测表现。fht指标预测能力最为突出，可以有效预测所有时段的股票超额收益，其中对半年后的股票超额收益预测能力最强，拟合优度达到987%，表现远远优于传统的预测因子。与fht指标类似，zeros指标和prin指标同样对半年后超额收益预测能力最佳。价格影响测度ami无法有效预测一个月及一季度后的超额收益，但却可以预测半年后和一年后的超额收益，且在一年期预测模型中表现最佳。下栏展示了经过Bootstrap调整的β^*以及对应的P值（拒绝比）。大部分指标经过调整的β^*与原始的β^差别极小，长记忆性及残差相关性对回归影响有限;cs指标和roll指标的回归结果受误差干扰较大，回归结果不可信。在具有Bootstrap稳健预测能力的非流动性指标中，fht指标、zeros指标、prin指标、ami指标和市场预期收益均呈正相关，即当期的流动性越差，市场预期收益越高，从非流动性测度的角度证明了沪深300市场中流动性溢价现象的存在。并且，prin等非流动性因子优异的预测表现证明了本文的假设：非流动性因子是多因子定价理论的重要因子。

（二）样本外预测能力分析

经过Bootstrap抽样得到偏差调整斜率及具有稳健预测能力的非流动性指标后，本文将经过调整的β应用于样本外检验以衡量非流动性指标的实战能力。通过比较预测值偏差以及历史基准值偏差，从而评估非流动性指标的样本外预测能力。具体而言，将（t+1）期实际收益yt+1作为预测目标，依据AR（1）预测模型得未来股票超额收益记为y^t+1，得到相應的样本均根预测误差（MSPE），同理得基准样本均根预测误差。

σ^2≡P-1∑（yt+1-y^t+1）2

σ^2BMK ≡P-1∑（y^t+1 -y^BMKt+1）2（12）

其中P代表样本外预测滚动次数，将历史收益的平均值作为未来一期股票超额收益预测值y^BMKt+1，yt+1为实际收益。

为了更直观地比较两个预测偏差，引入样本外拟合优度R2OOS[20]，样本外拟合优度R2OOS越大表明预测模型偏差相对基准模型偏差越小，即非流动性指标预测能力越强。本文还应用了Clark & West以及Giacomini & White使用的样本外表现评价方法[21，22]，模型如下：

R2OOS = 1-σ^2σ^2BMK

CW=σ^2BMK-σ^2+P-1∑（y^t+1-y^BMKt+1）2Adjustment

Giacomini-White=σ^2BMK-σ^2σ^p/P（13）

其中，σ^p为渐进方差^σ2p的异方差自相关一致性（HAC）估计值，σ^2p=var[P（σ^2BMK-σ^2）]。本文选择了48个月的滚动周期进行样本外检验，应用递增窗口回归分别得出样本外拟合优度R2OOS、CW值以及GW值。若所得结果大于0，则说明非流动性指标的预测能力优于历史基准，可以拒绝非流动性指标没有预测能力的零假设;CW值以及GW值越大，表示非流动性指标的样本外预测能力越强。

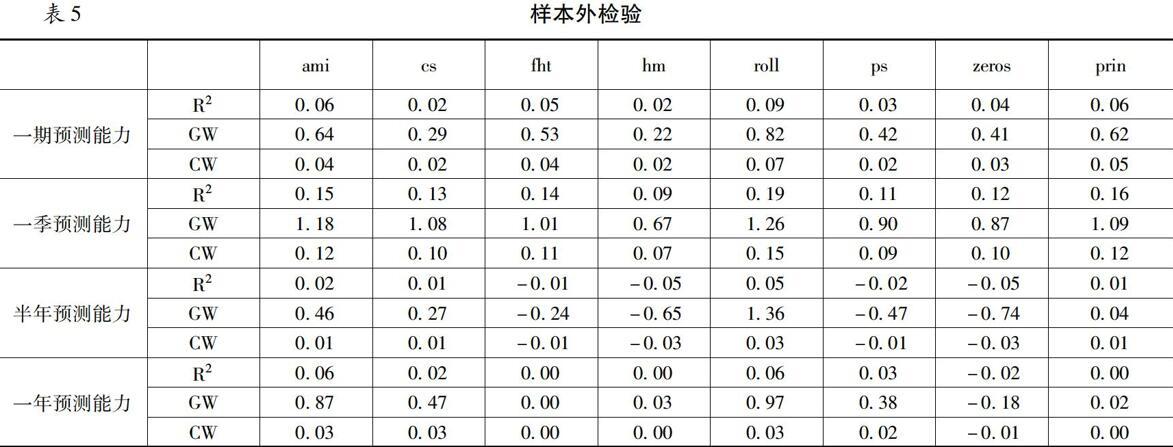
表5展示了非流动性指标的样本外预测表现。在一期及一季度预测中，所有非流动性指标的R2OOS、CW值及GW值均大于0，说明非流动性指标对超额收益的短期预测能力均优于历史基准;而在半年期及一年期的预测中，非流动性指标的表现出现分化，其中ami指标、roll指标、cs指标以及prin指标预测表现优于历史均值模型，而其他指标预测表现不及历史均值模型。因此，在样本内检验中表现较好的prin和ami等指标，在样本外检验中同样能够对超额收益进行有效预测。非流动性因子ami及综合因子prin不仅在样本内检验中具有优良的预测能力，且能够对超额收益率进行有效的样本外预测，证明了非流动性是多因子定价理论中的重要一环。

五、稳健性检验

Merton发现，即使市场交易成本较低时，收益率的波动性仍然会造成风险溢价。[23]因此本节对非流动性指标进行波动性调整，剔除非流动性指标中波动性的部分，检验其剩余部分对股票未来收益的预测能力。采用回归法对非流动性指标进行波动性调整，参照下式进行回归获得回归残差εt，取残差部分即为剔除市场波动后的非流动性指标。

ILQt=α+βvolt+εt（14）

其中，ILQt为任意非流动性指标，volt为市场波动指标。

剔除市场波动因素后的非流动性指标预测结果如表6所示。一期及一季度预测中，fht指标仍然具有显著的预测能力，但zeros指标和prin指标与未来一期的股票收益不再有显著相关性。然而，在中、长期预测能力评估中，ami指标、fht指标、zeros指标、prin指标和roll指标预测表现得到改善。Bootstrap稳健检验中除cs指标的预测偏差较大之外，其他非流动性指标的预测结果均可信，而在样本内检验中预测偏差较大的roll指标剔除波动因素后通过Bootstrap稳健检验，表明市场波动的长记忆性同样会造成预测偏差。综上可知，非流动性指标的预测能力是稳健的，剔除波动率的流动性因子仍然是重要的定价因子。

六、结论

本文从非流动性的内涵出发，使用7个反映不同方面的非流动性测度以及综合性非流动性测度对超额收益进行短、中及长期预测分析。研究发现：非流动性指标兼具对未来收益的短期预测能力和中长期预测能力，其中fht指标表现出色，比起传统流动性指标预测表现中1% 上下的拟合优度，fht指标在半年期的预测中拟合优度达到987%，对一季度后超额收益预测的拟合优度也有771%，验证本文假设，即非流动性因子是因子定价理论的重要因子;其次，长记忆性及残差相关性会对预测显著性造成干扰，cs指标及roll指标因长记忆性造成的误差较大，回归结果不可信;大多数测度斜率为正，符合流动性风险溢价理论预期。

以上研究结论具有一定的理论与实践意义：第一，证明非流动性因子是多因子定价理论的重要因子。自单因子CAPM模型向多因子定价模型发展以来，针对各类因子的研究层出不穷，但对非流动性因子尤其是综合非流动性涉足甚少。本文以多个非流动性因子对短、中及长期超额收益率预测发现，非流动性是因子定价理论中重要的一环，fht， prin及ami等非流动性因子能够对超额收益率进行有效的解释及预测，其中fht指标在半年期的预测中拟合优度达到987%，prin的拟合优度也高达816%，远远超过传统流动性因子预测表现，丰富了多因子定价领域研究。第二，经过Bootstrap调整后的斜率更加准确，且非流动性测度与未来市场超额收益斜率基本皆为正数，较为严谨地证明了沪深300市场流动性风险溢价现象的存在;非流动性测度如fht、prin测度，其对市场超额收益预测能力远优于传统预测因子，对投资者决策具有一定的实践意义;大多非流动性指标对市场超额收益的短期预测能力来源于市场波动，而中长期预测能力由与波动无关的非流动性因素主导。

参考文献：

[1]张峥， 刘力. 换手率与股票收益：流动性溢价还是投机性泡沫？[J]. 经济学， 2006（2）： 871～892.

[2]Tirole J. Illiquidity and All Its Friends[J]. Journal of Economic Literature， 2011， 49（2）： 287～325.

[3]Roll R. A Simple Implicit Measure of the Effective Bid-Ask Spread in an Efficient Market[J]. Journal of Finance （Wiley-Blackwell）， 1984， 39（4）： 1127～1139.

[4]Corwin S A， Schultz P. A Simple Way to Estimate Bid-Ask Spreads from Daily High and Low Prices[J]. The Journal of Finance， 2012， 67（2）： 719～760.

[5]Pástor L， Stambaugh Robert f. Liquidity Risk and Expected Stock Returns[J]. Journal of Political Economy， 2003， 111（3）： 642～685.

[6]Hou K W， Moskowitz T J. Market Frictions， Price Delay， and the Cross-Section of Expected Returns[J]. Review of Financial Studies， 2005， 18（3）： 981～1020.

[7]Fong K Y L， Holden C W， Trzcinka C A. What Are the Best Liquidity Proxies for Global Research？[J]. Review of Finance， 2017， 21（4）： 1355～1401.

[8]Kyle A. Continuous Auctions and Insider Trading[J]. Econometrica， 1985， 53（6）： 1315～35.

[9]Amihud Y. Illiquidity and Stock Returns： Cross-Section and Time-Series Wffects[J]. Journal of Financial Markets， 2002， 5（1）： 31～56.

[10]Chen Y， Eaton G W， Paye B S. Micro（structure） before Macro？ The Predictive Power of Aggregate Illiquidity for Stock Returns and Economic Activity[J]. Journal of Financial Economics， 2018， 130（1）： 48～73.

[11]Chen S S， Chou Y H， Yen C Y. Predicting US Recessions with Stock Market Illiquidity[J]. B E Journal of Macroeconomics， 2016， 16（1）： 93～123.

[12]王春峰， 韓冬， 蒋祥林. 流动性与股票回报：基于上海股市的实证研究[J]. 经济管理， 2002（24）： 58～67.

[13]闫东鹏， 吴贵生. 流动性和可预测股票回报：一个实证检验[J]. 统计研究， 2006（08）： 66～71.

[14]黄峰， 杨朝军. 流动性风险与股票定价：来自我国股市的经验证据[J]. 管理世界， 2007（05）： 30～39;48.

[15]谢赤， 张太原， 曾志坚. 中国股票市场存在流动性溢价吗？——股票市场流动性对预期收益率影响的实证研究[J]. 管理世界， 2007（11）： 36～47.

[16]Fama E F， French K R. The Cross-Section of Expected Stock Returns[J]. The Journal of Finance， 1992， 47（2）： 427～465.

[17]Fama E F， French K R. A Five-Factor Asset Pricing Model[J]. Journal of Financial Economics， 2015， 116（1）： 1～22.

[18]Goyenko R Y， Holden C W， Trzcinka C A. Do Liquidity Measures Measure Liquidity？[J]. Journal of Financial Economics， 2009， 92（2）： 153～181.

[19]Stambaugh R F. Predictive Regressions[J]. Journal of Financial Economics， 1999， 54（3）： 375～421.

[20]Campbell J， Thompson S P. Predicting Excess Stock Returns Out of Sample： Can Anything Beat the Historical Average？[R]. Harvard University Department of Economics， 2008.

[21]Clark T E， West K D. Approximately Normal Tests for Equal Predictive Accuracy in Nested Models[J]. Journal of Econometrics， 2007， 138（1）： 291～311.

[22]Giacomini R， White H. Tests of Conditional Predictive Ability[J]. Econometrica， 2006， 74（6）： 1545～1578.

[23]Merton R C. An Intertemporal Capital Asset Pricing Model[J]. Econometrica， 1973， 41（5）： 867～887.

The predictive power of aggregate illiquidity for stock returns

- based on ARFIMA model

XIE Jun1，HU Nan1，GAO Bin2，LUO Tiantian1

（1.School of Business，Guangxi University， Nanning， Guangxi 530000， China;

2.School of Economics， Guangxi University for Nationalities， Nanning， Guangxi 530000， China）

Abstract：From the concept of illiquidity， we calculate seven illiquidity proxies by using samples from Shanghai and shenzhen stock exchange （csi） 300， and use principal component analysis （pca） to obtain the comprehensive illiquidity proxy（prin）. We use ARFIMA model to fit the long memory and residual correlation of various variables， monte carlo simulation is constructed to measure the influence of long memory and residual correlation on prediction regression， and Bootstrap sampling method is used to adjust the deviation and screen the illiquidity measure with robust prediction ability. The results show that： the illiquidity measure can predict the short， medium and long term excess returns， R2 measures of fht and prin are high， which reflects that the important role of illiquidity factor in liquidity risk pricing; The short-term forecasting ability of most illiquidity indexes to the market excess returns comes from the market volatility， while the medium-term and long-term forecasting ability is dominated by the illiquidity factors which have nothing to do with the volatility.

Key words：illiquidity;long memory;equity premium;market volatility

責任编辑：萧敏娜 吴锦丹 萧敏娜 常明明 张士斌 张建伟 张领

收稿日期：2020-07-12

基金项目：国家自然科学基金（72061002）;国家社科基金后期资助项目（18FJY009）;广西自然科学基金青年项目（2018JJB180007）;教育部人文社会科学研究西部和边疆地区项目（18XJC790003）。

作者简介：谢军（1980—），男，广西桂林人，广西大学商学院副教授，博士，研究方向为行为金融、资产定价;胡楠（1994—），男，安徽蚌埠人，广西大学商学院硕士研究生，研究方向为资产定价、股票预测（通讯作者）;高斌（1984—），男，山东青岛人，广西民族大学经济学院副教授，博士，研究方向为行为金融、金融计量;罗恬恬（1995—），女，江西南昌人，广西大学商学院硕士研究生，研究方向为资产定价、股票预测。