新能源汽车永磁同步电机最大转矩电流比控制

杨家印

（江苏联合职业技术学院徐州经贸分院，江苏 徐州 221004）

由于永磁同步电机具有效率高、功率密度大等诸多优点，近年来其被广泛应用于新能源电动汽车、新能源发电等领域[1-3]。

与隐极式永磁同步电机相比，凸极式永磁同步电机可以通过利用磁阻转矩进一步增大转矩输出，因此特别适用于新能源汽车、数控机床等要求电机具有高功率密度的场合[4-5]。

为了充分利用凸极式永磁同步电机的磁阻转矩，实现最大转矩电流比控制，近年来，诸多学者开展了相关研究。

目前，常用的凸极式永磁同步电机最大转矩电流比控制方法主要包括3类，即直接公式计算法、基于查表的最大转矩电流比控制方法和采用定子电流矢量角自校正的控制策略[6]。

公式法是根据电机在最大转矩电流比点运行的约束条件，通过电磁转矩方程计算当前矢量角的一阶导数，然后令导数为零可得出最优电流角度的计算公式。这个方法虽然看似简单，但是其计算式中包含了很多电机参数，电机参数一定且准确时，运用公式才是正确的。但在实际运行中，电机参数会受温度等因素的影响而发生变化，所以公式法计算精度不高[7-10]。

为了解决公式法存在的计算复杂、且精度较低的问题，一些研究人员提出了基于查表的方法，即按照最大转矩电流比控制方法的转矩和定子电流之间的关系，将对应于各种转矩数值的d，q轴电流设定值列成表格。通过查表法，给出最大转矩电流比所需的d，q轴电流。尽管查找表的方法避免了复杂的计算方法，但它同时也增加了大量的离线测试以获取表中的数据，并且需要占用额外的存储资源。离线测试依然要基于电机做测试，对电机参数依然具有依赖性，因此并不能避免公式法的缺点[11]。

采用定子电流矢量角自校正的最大转矩电流比控制策略在稳态运行条件下，当给定转矩时，以较小的步幅缓慢改变电流矢量角设定值，然后比较定子电流对应的不同矢量角的幅值。经过多次比较后，在线获得给定转矩下所需的最小电流及其矢量角，从而实现最大转矩电流比控制。该方法有效地避免了由于参数变化所产生的影响。然而，由于不断地扰动，其转矩稳态控制精度较差[12-15]。

针对上述问题，本文以新能源电动汽车永磁同步电机为研究对象，为了提高电机最大转矩电流比控制的控制精度、增强其对参数变化的鲁棒性，提出了一种基于高频信号注入的永磁同步电机最大转矩电流比控制新方法。所提方法通过注入一个高频信号，并进行处理，从而实现最大转矩电流比控制，并消除了参数变化的影响。仿真和实验结果均验证了所提方法的有效性，能够为新能源电动汽车永磁同步电机或相近使用场合提供借鉴。

1 常规最大转矩电流比控制方法

在同步旋转d-q坐标系下，永磁同步电机的数学模型可表示为

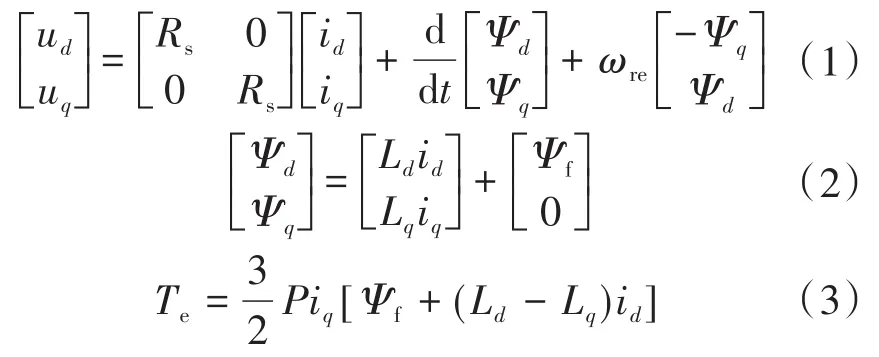
式中：ud，uq分别为 d-q坐标系下的定子电压；id，iq分别为d-q坐标系下的定子电流；ωre为电气角速度；Ψd，Ψq分别为d-q坐标系下的定子磁链；Ψf为转子磁链；Ld，Lq分别为d-q坐标系下的直轴电感、交轴电感；Rs为定子电阻；P为极对数；Te为电磁转矩。

由式（3）可知，电磁转矩Te与定子电流id，iq有非线性关系。常规的矢量控制常采用id=0的控制方法，此时，转矩Te与iq为线性关系。然而，此时凸极式永磁同步电机的磁阻转矩没有得到充分利用。为了充分利用磁阻转矩，实现最大转矩电流比控制，可根据式（3）优化电流id，iq的分配方法，实现输出同样转矩时电流幅值最小，从而可减小铜耗。

图1给出了定子电流矢量关系，其数学表达式如下式所示：

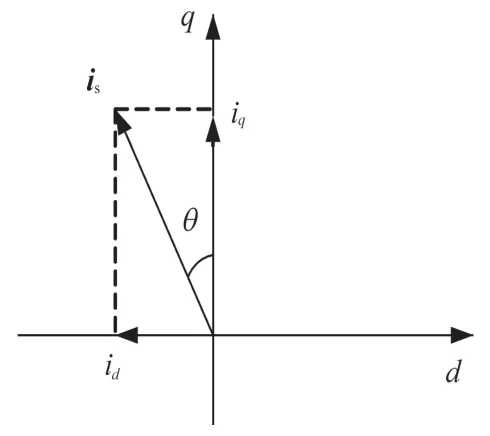
图1 定子电流矢量关系Fig.1 Relationship of the stator current vector

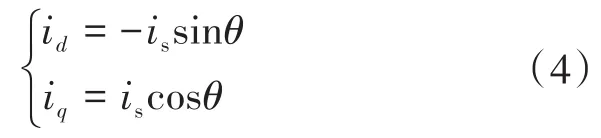
式中：is为定子电流幅值；θ为电流矢量角。

结合式（3）和式（4）可得：

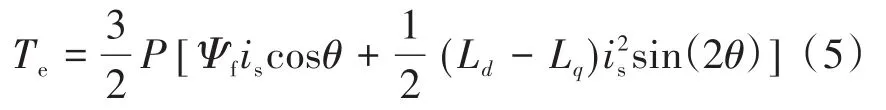
求电磁转矩对电流角的偏导数可得：

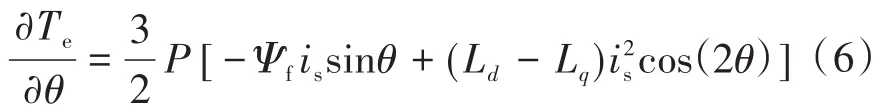
当实现最大转矩电流比控制时，要求式（6）为零。由此可得：

结合式（7）和式（4）可得：

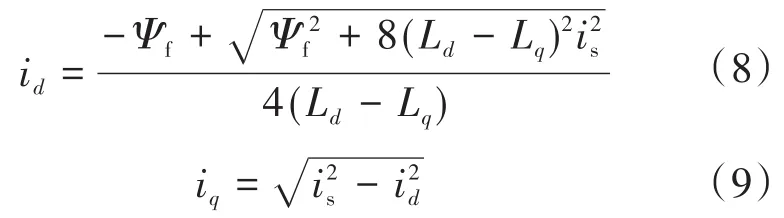
式（8）和式（9）给出了基于直接计算法实现最大转矩电流比控制的电流分配方法。虽然理论上该方法可以实现电流的最大转矩电流比控制，但是，由式（8）和式（9）可知，该方法对电机电感和磁链参数有较强的依赖性。为了解决该问题，本文提出了一种基于高频信号注入的永磁同步电机最大转矩电流比控制方法。

2 所提最大转矩电流比控制方法

2.1 基本原理

本文所提方法的实现原理是将高频、小幅值的电流角信号注入系统，将电磁转矩与电流角的关系表达式按泰勒公式展开，然后经过带通滤波器、低通滤波器滤掉多余频率的部分，最终得到只含有转矩的一阶偏导数的部分，并将其积分结果当做直轴电流参考值。如果此时没有工作在最大转矩电流比点，转矩对电流角的一阶偏导数不等于零，积分器会继续积分，调整直轴参考电流，直到它工作在最大转矩电流比点，即转矩对电流角的一阶偏导数为零为止，直轴参考电流因为PI控制器输入为零而保持上一个状态不变，电机继续运行在最大转矩电流比点，即实现最大转矩电流比控制。

当电流矢量中注入一个频率为ωh，幅值为A的高频正弦波信号时，可将电磁转矩与含有高频量的电流角[θ+Asin（ωht）]的关系式按泰勒公式展开如下：

最大转矩电流比控制的实现是使电磁转矩对电流角的一阶偏导数为零。注入电流角信号之后得到如式（10）所示的电磁转矩表达式，然后经过带通滤波器和低通滤波器，最终得到只含有电磁转矩对电流角的偏导数项的部分。当电磁转矩表达式中注入高频分量后，若要最终留下转矩对电流角的一阶偏导数来实现最大转矩电流比控制，就需要对式（10）作如图2所示的信号处理。

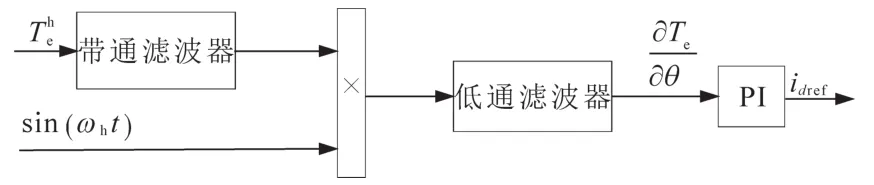
图2 信号处理方法Fig.2 Signal processing method

在图2中，将含有高频分量的电磁转矩的泰勒表达式经过带通滤波器可得到含有Asin（ωht）项的部分，其他频率的信号都被衰减甚至滤除，然后再与sin（ωht）相乘，得到含有sin（ωht）二次项的部分，展开得到如下式所示的结果：

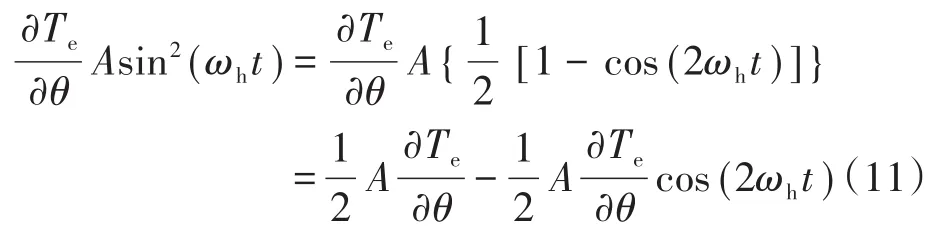
式（11）经过低通滤波器，剩下只含有常数项的部分，即得到电磁转矩关于电流角的一阶偏导数。若此时没有工作在最大转矩电流比点，即Te对θ的偏导数不为零，积分器会继续积分，直到工作在最大转矩电流比点，此时积分器保持上一输出，作为直轴参考电流idref，如图2所示。

当注入高频、小幅值的电流角扰动信号后，d，q轴电流中会含有高频分量，此时的电流表达式如下：

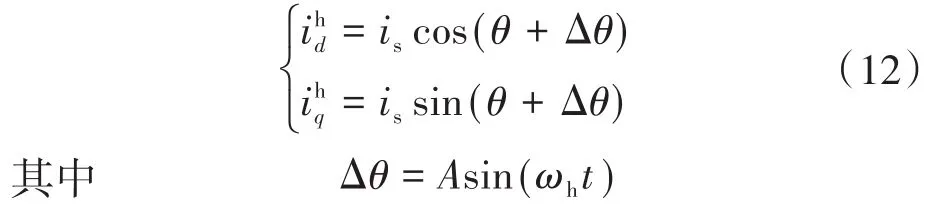
将式（12）代入式（3）中，可得：

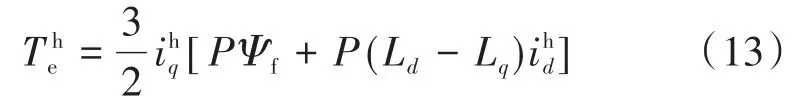
由此进一步可得完整的高频信号注入和处理方法控制框图，如图3所示。含所提基于高频信号注入的最大转矩电流比控制方法的整体控制框图如图4所示。

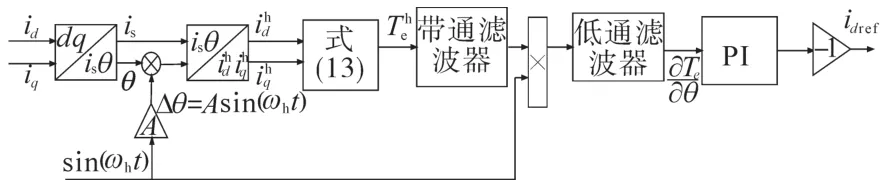
图3 高频信号注入和处理方法控制框图Fig.3 Control block diagram of high frequency signal injection and processing method

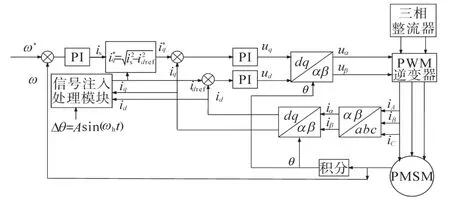
图4 整体控制框图Fig.4 The whole control block diagram

2.2 滤波器设计

上述流程中的关键点在于对加入的高频信号的处理，要从众多的杂波中滤掉流程所不需要的部分，才能使整个流程顺利完成，实现最大转矩电流比控制。

带通滤波器是指能通过某一特定频率范围内的频率分量，并将其他范围的频率分量衰减到非常低水平甚至消除的滤波器。本文注入的高频信号频率为500 Hz，幅值为0.075，所以带通滤波器的中心频率为500 Hz。本文所设计的带通滤波器传递函数为

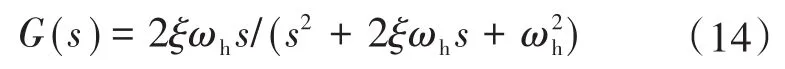
式中：ωh为中心频率，取1 000π；ξ取0.707。

低通滤波器的原理是允许截止频率以下的频率信号通过，而高过截止频率的高频信号则被阻隔并减弱而不能通过。低通滤波可以简单的认为：设置一个频率点，当频域高于这个截止频率时，则全部赋值为零。在这个过程中，所有的低频信号都会通过，这就是所谓的低通滤波。本文使用低通滤波器主要是为了使式（11）经过低通滤波器后只留下电磁转矩的一阶偏导数，最后经过PI控制器输出作为直轴参考电流。因此，所设计的低通滤波器的传递函数如下式：

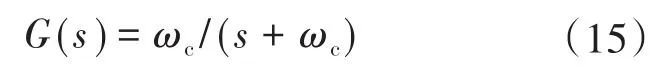
式中：ωc为截止频率，本文选择其为100π。

3 仿真研究

为验证算法的有效性，利用Matlab/Simulink进行了仿真验证，仿真所使用的参数为：d轴电感0.024 H，q轴电感0.044 H，永磁体磁链0.5 Wb，定子电阻0.6 Ω。首先，为了验证所提方法的有效性，在转速为500 r/min、负载转矩为30 N·m的条件下对所提方法进行了仿真验证，并与直接计算法进行了对比。所提方法的直轴电流id波形如图5所示，直接计算法得到的仿真结果如图6所示。

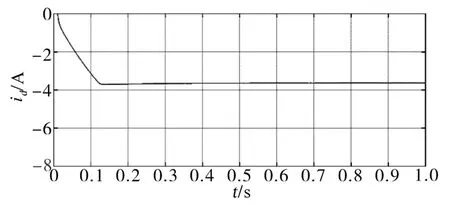
图5 本文所提方法的电流idFig.5 The current idof the proposed method

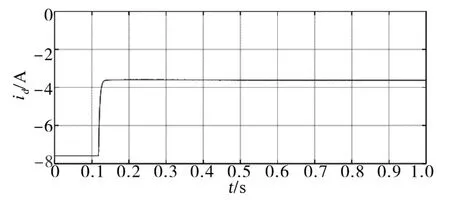
图6 直接计算法的电流idFig.6 The current idof the direct computing method

由图5和图6可见，本文所提方法可以获得与直接计算法完全相同的稳态电流结果，这就验证了所提方法的有效性。区别于直接计算法，本文所提方法不需要根据电机参数进行在线计算，因此，其鲁棒性更强。

为了进一步验证本文所提方法的优点，进一步通过仿真与直轴电流id=0的方法进行了对比。在该仿真中，电机转速由0加速至500 r/min，速度环输出电流的限幅值为20 A。转矩、电流和转速仿真结果如图7和图8所示。

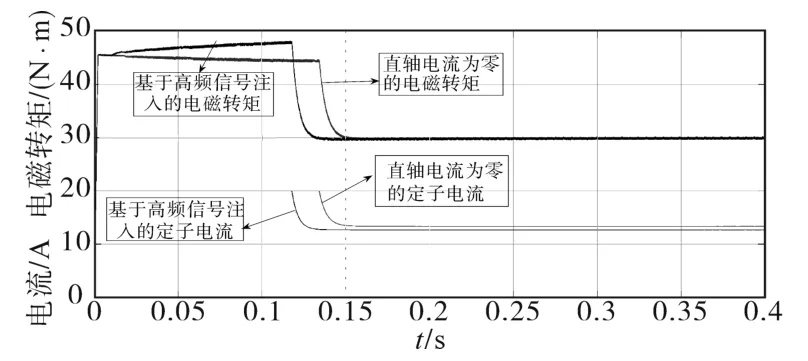
图7 转矩和电流波形Fig.7 The waveforms of the torque and the current

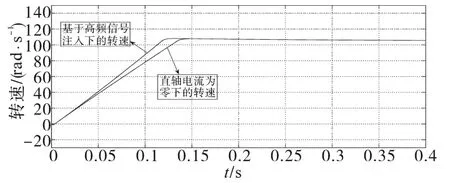
图8 转速波形Fig.8 The waveforms of the speed

由图7前段动态部分可见，在定子电流一定的情况下，基于高频信号注入的最大转矩电流比控制策略的电磁转矩大于id=0控制策略下的电磁转矩，这是因为前者合理地运用了磁阻转矩，重新分配了直轴和交轴的电流，使电磁转矩达到最大。这也验证了本文所提方法的有效性。此外，由图7后段稳态结果可见，在有一定的电磁转矩的情况下，基于高频信号注入的最大转矩电流比控制策略的定子电流小于id=0控制策略下的定子电流。同样也是因为前者充分利用了交、直轴电感不同而产生的磁阻转矩，在达到相同的电磁转矩时，基于高频信号注入的最大转矩电流比控制策略会比id=0控制策略需要更小的定子电流，以达到提高电机效率的目标。因为两种方法的负载相同，所以当系统达到稳定时，两者的电磁转矩相同。由图8可知，在相同的条件下，基于高频信号注入的最大转矩电流比控制策略的转速要大于id=0控制策略下的转速，这是因为基于高频信号注入的最大转矩电流比控制策略中电磁转矩较大，所以转速加速过程要快于id=0控制策略下的转速。同时，电机转速达到稳态所需的时间更短。

4 实验研究

为了进一步验证所提方法的正确性，建立了如图9所示的实验平台，并进行了实验研究。实验所用电机参数与仿真一致。

图9 实验平台Fig.9 Experimental platform

图10给出了电机转速为500 r/min，负载转矩为30 N·m时，施加本文所提方法前后的电流波形。由图10清晰可见，施加本文所提方法后，在负载转矩不变的前提下，电机的定子电流幅值得到减小，这就验证了本文所提方法的有效性。

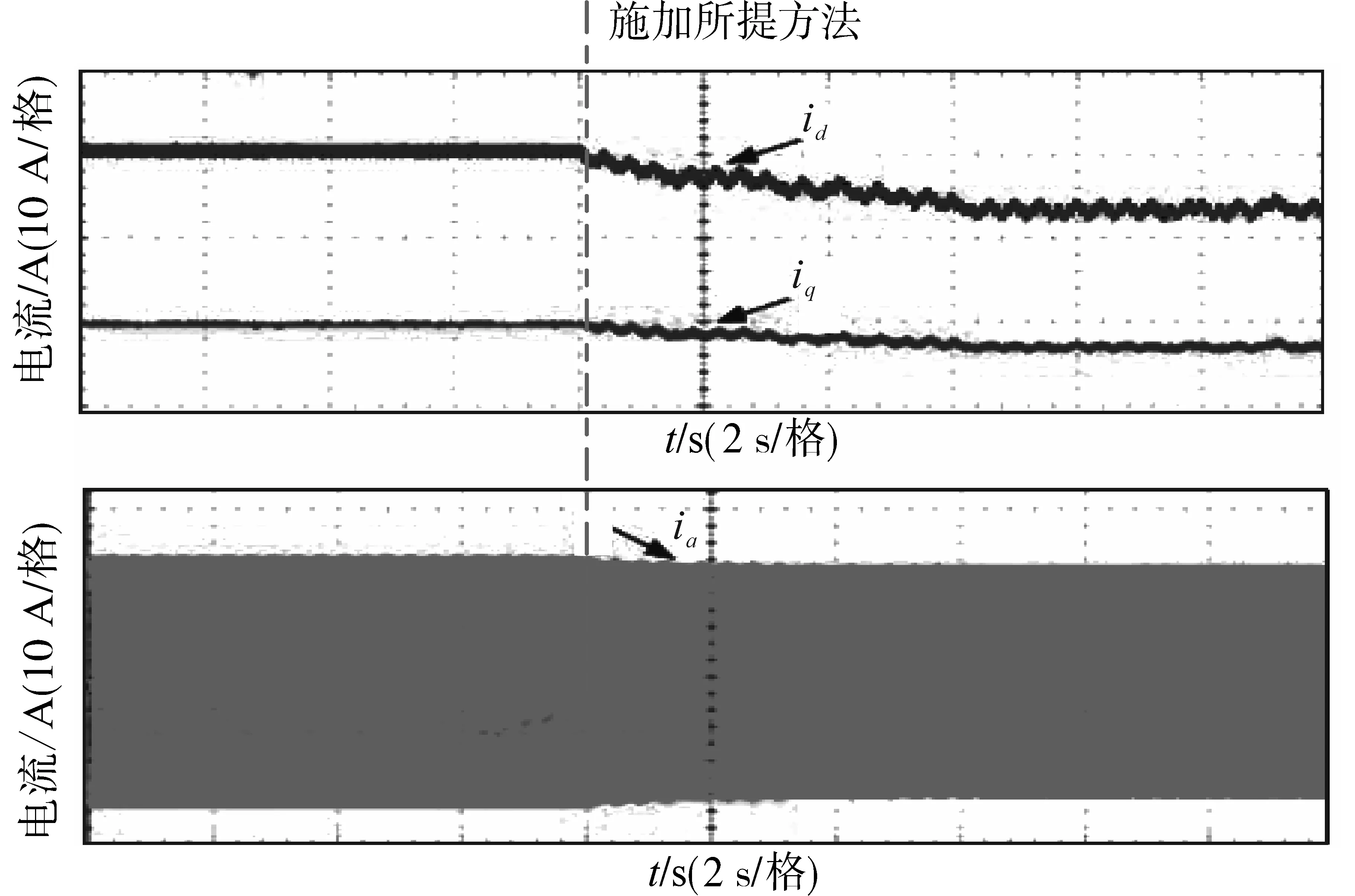
图10 本文所提方法实验结果Fig.10 Experimental results of the proposed method

5 结论

针对永磁同步电机的最大转矩电流比控制问题，提出了一种基于高频信号注入的最大转矩电流比控制新方法。详细给出了所提最大转矩电流比控制方法的基本原理和实施方法，并通过仿真和实验对所提方法进行了对比验证。仿真和实验结果都表明所提方法可以获得与直接计算法相同的控制效果，但所提方法对参数变化具有更强的鲁棒性。同时，与常规id=0的控制相比，仿真和实验结果均表明所提方法可以在负载转矩固定的前提下实现定子电流最小化控制，这进一步验证了所提方法的有效性。与常规基于直接计算的最大转矩电流比控制相比，所提方法避免了使用电机参数，因此可以明显提高最大转矩电流比控制的参数鲁棒性。但是，由于所提方法需要额外的注入高频信号，因此与常规基于直接计算的最大转矩电流比控制相比，所提方法也会增大转矩脉动，这也是所提方法的主要缺点。在今后的研究中，如何降低转矩脉动仍需深入研究。