基于ELM与DWT的电能质量检测技术研究

凌万水，刘刚

（1.上海金智晟东电力科技有限公司，上海 200233；2.国网江苏省电力有限公司宿迁供电分公司，江苏 宿迁 223800）

作为一个高度复杂的网络，智能电网在运行过程中需要先进的监测系统维持其可靠性、安全性与可持续性地工作。随着工业物联网（internet of things，IoT）等概念的提出，智能电网将产生越来越海量的数据，这也对快速有效的数据处理与挖掘提出更高要求[1]。此外，当今的智能电网体系正在连接越来越多样化的基本单位，如各类可再生能源与高级计量设施（advanced metering infrastructure，AMI）等[2]。由于工业社会与电网的高度耦合，停电等电能质量问题会造成重大损失。

在电能质量监测领域，电能质量事件（power quality event，PQE）分类是一个关键问题。一般地，PQE分类分为特征提取与决策两个阶段。在特征提取阶段，使用信号处理技术将电能质量（PQ）信号转换到特定的特征空间并提取特征，然后在决策阶段基于特征使用各种分类模型完成分类。特征空间的形式取决于特征变换中使用的方法，如基本的快速傅里叶变换（fast Fourier transform，FFT）与均方根（root mean square，RMS）变差跟踪等[3-4]。这两类方法在时域分析问题中不适用，短时傅里叶变换（short-time FFT，STFFT）对此进行了改进，使FFT具备了时域分析能力[5]。更为复杂的方法包括卡尔曼滤波器、Hilbert-Huang变换与S变换等[5-7]。在决策阶段，由于PQE检测本质上是分类问题，因此可以使用机器学习中常见的分类算法处理，如深度神经网络（deep neural network，DNN）与支持向量机（support vector machine，SVM）等[8-9]。

本文提出一种基于离散小波变换（discrete wavelet transform，DWT）与极限学习机（extreme learning machine，ELM）的PQE分类技术。在特征提取中，该方法将熵引入到小波变换的计算中，并结合直方图表示可以更为快速地提取特征集合。在决策阶段，建立非迭代的极限学习机模型，在保证模型性能的同时，通过省略迭代学习过程进一步提升效率。本文方法的优势包括：

1）在特征提取的效果上，在离散小波变换的基础上，引入了熵和直方图特征，进一步丰富了特征集；

2）在分类效率上，使用高效的极限学习机模型，该模型可以直接求解而无需梯度下降等迭代优化过程，在计算速度上具有显著优势。

1 特征选择

1.1 基于小波与熵的特征选择

小波变换的思想来源于ST-FFT，通过对信号进行自适应“时间-频率”窗口大小的变换，克服了ST-FFT仅能以固定宽度的窗口探测信号的局限性，从而可以揭示信号的深层次细节特征[10]。这一特点使小波变换可以基于不同的分辨率级别对信号波形进行灵活的时-频分析，即进行多尺度分析（multi-resolution analysis，MRA）。MRA易于在波形中发现事件的起点和终点，因此小波变换在PQE检测与分类等问题中有丰富的潜在应用场景[11-12]。

与傅里叶变换类似，小波变换可以应用到离散信号（DWT）。DWT的形式为

式中：a为频率缩放系数；b为时间偏移常数；y（t）为被处理的信号；ψ（t）为离散小波函数。

离散信号通过将信号划分为多个频段进行多尺度分析。但实际上信号会覆盖无限宽度的频率，因此一般只在一定频率范围内处理。本文使用8级分解的DWT，选取的小波函数为“Daubechies 4”（db4）小波[13]。图1给出了DWT在样本信号上进行MRA的一个例子，其中s为原始信号，d1～d8为8级分辨率的检测结果。可以看出，d1～d4已经可以清晰地检测出PQE在时域上的范围。

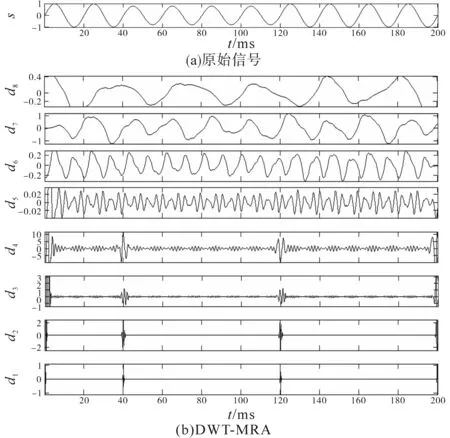
图1 基于DWT的8级多尺度分析Fig.1 8-level multi-resolution analysis based on DWT

在将信号输入分类器之前，需要对信号作规模缩小处理。在这一步骤本文引入基于熵的方法。在信号处理中，熵可用于表征一个非平稳信号的无序程度，常用于信号的熵定义包括香农熵、阈值熵、规范化熵与对数能量等[14-15]。图2仅以数据集中最典型的四种PQE类型（暂降（Sag）、暂升（Swell）、谐波（Harmonic）与中断（Interruption））为例，给出了样本PQE的熵的图示，图中横轴为MRA的尺度级别，纵轴为对应的熵值。可以看出，熵特征较好地对PQE进行了表征，并区分出不同类型的PQE。

对于信号y，其香农熵的定义为

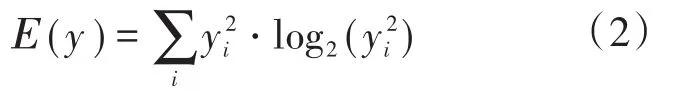
式中：yi为第i个分量。

对每个PQE的DWT系数向量计算熵，即可生成8个特征，见图2。

图2 样本PQE的8级DWT熵特征Fig.2 8-level DWT-entropy feature of sample PQEs

1.2 直方图特征提取

直方图可用于图形化地表示一定长度范围内事件的计数。图3以四种样本PQE为例，说明直方图可以直观地体现各种PQE的分布情况，使其特征更为显著。图中横轴为归一化的幅度。

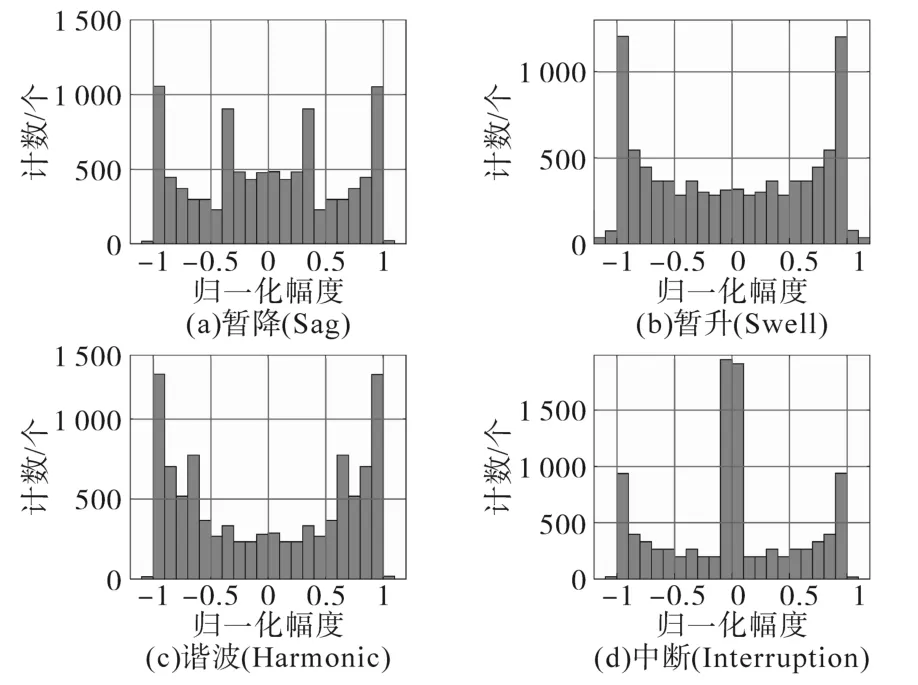
图3 样本PQE的直方图Fig.3 Histogram of sample PQEs

本文使用Sturges规则确定直方图中的每个区间并进行事件计数[16]。具体地，直方图特征集由每个PQE的14个分量构成，该值（记为C）由如下的经验公式确定：

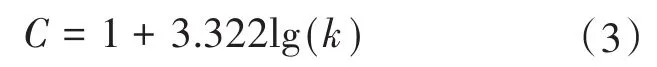
式中：k为每个信号的样本个数。

图4给出了四种PQE的直方图特征。

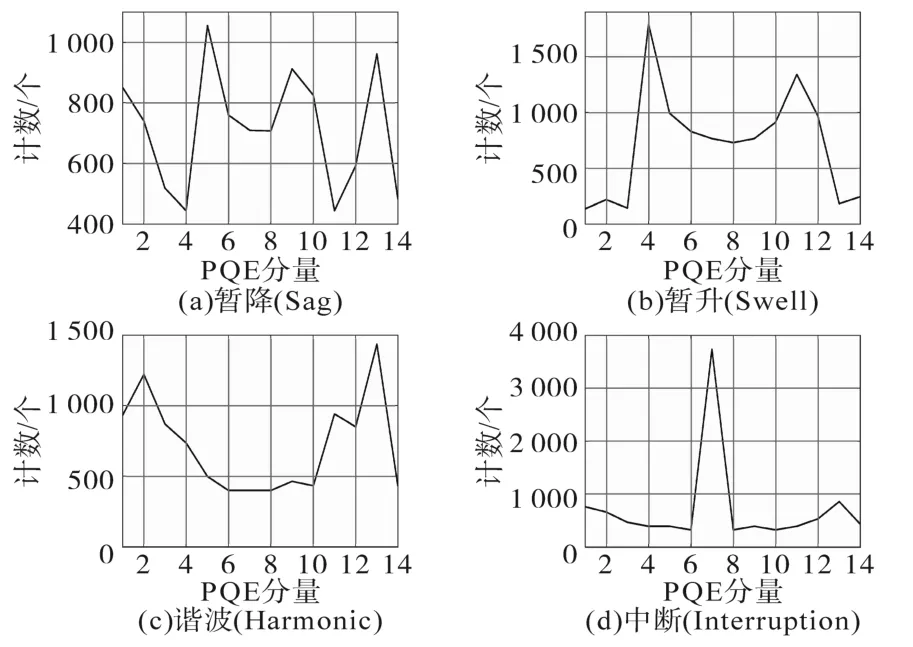
图4 样本PQE的直方图特征Fig.4 Histogram features of sample PQEs

由图4可以看出，直方图特征可以有效地区分四种PQE，其中横轴表示信号的各个分量。

2 极限学习机

极限学习机（ELM）最早作为单隐层前馈神经网络（single-hidden layer feedforward neural network，SLFN）的一种学习范式而被提出[17]。在ELM中，输入层的权值与偏置都是随机分配的，只有输出值会被计算，因此，ELM的计算时间极短。此外，与传统的前馈神经网络（feed forward artificial neural networks，FF-ANN）相比，ELM具有更强的泛化能力[18-19]。图5展示了一个基本的SLFN结构，其中xj与yj分别表示网络输入与输出。

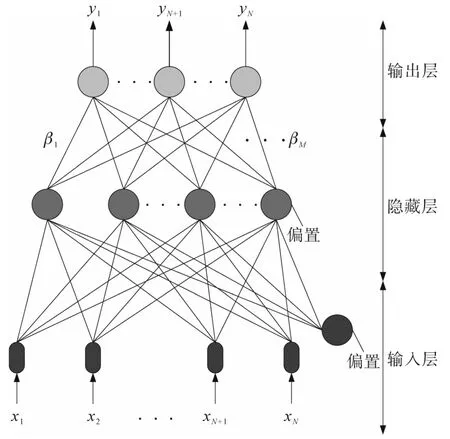
图5 单隐层前馈神经网络Fig.5 Single-hidden layer feedforward neural network

隐藏层包含M个结点，且激活函数为g（x）的SLFN可以表示为

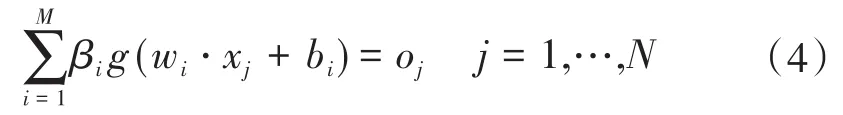
式中：w为输入层权值；b为输入层偏置；β为输出层偏置；o为网络的预期输出。

由于SLFN在理论上是零误差的，因此可以直接用y替代o，即

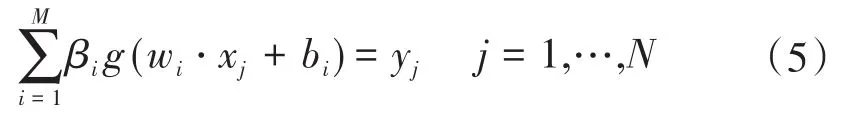
这表明存在合适的权值与偏置使SLFN的实际输出与真实值一致，上述过程简化可得：

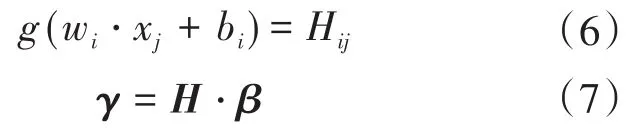
式中：Hij为隐藏层的输出。

求解线性方程式（7）即可得到合适的权值与偏置，其中γ为类别标签矩阵，H为隐藏层输出构成的矩阵。对于一般的神经网络，需要使用反向传播等迭代算法求解参数，但ELM仅需一次计算而无需任何迭代过程。其解决方案如下式：

3 实验结果与分析

3.1 数据集

本文使用的数据集采集自AMI设备在实际场景下检测到的信号，除用于举例的四类PQE之外，还包含了闪变（flicker）类样本。再加上普通信号，数据集中一共包括6类事件样本。经过采样，所有原始信号样本的长度都为10001，在特征提取后，特征的维度相比原始数据大幅降低。因此分类器所处理的实际上是22维的特征集合。图6给出了数据集中三个PQE信号的波形。

图6 样本PQE信号Fig.6 Sample PQE signals

3.2 实验结果

使用小波-熵以及直方图方法对数据集进行特征提取后，基于ELM进行PQE分类过程。22维的特征向量包括8级MRA提取的特征（记为E1～E8）与直方图方法提取的14维特征（记为H1～H14）。

实验中采用10折交叉验证评估模型性能，用于对比实验的模型为使用sigmoid激活函数的深度神经网络（deep neural network，DNN），所有实验在一台RAM为32 GB的工作站上进行。

表1给出了两种模型在信噪比（signal-noise rate，SNR）分别为30 dB，20 dB，10 dB时的PQE分类准确率。在经过充分的参数优化后，两种模型的准确性都达到了较高的水平，但ELM依然表现出优势。并且，由于ELM不需要迭代优化过程，因此在训练时间上大幅降低。值得注意的是，在20 dB噪声时，两种模型的性能相比10 dB噪声与30 dB噪声的情形都出现了下降，这可能是由于20 dB噪声恰好处在模型在数据集上保持鲁棒性的临界点附近所致[20]。

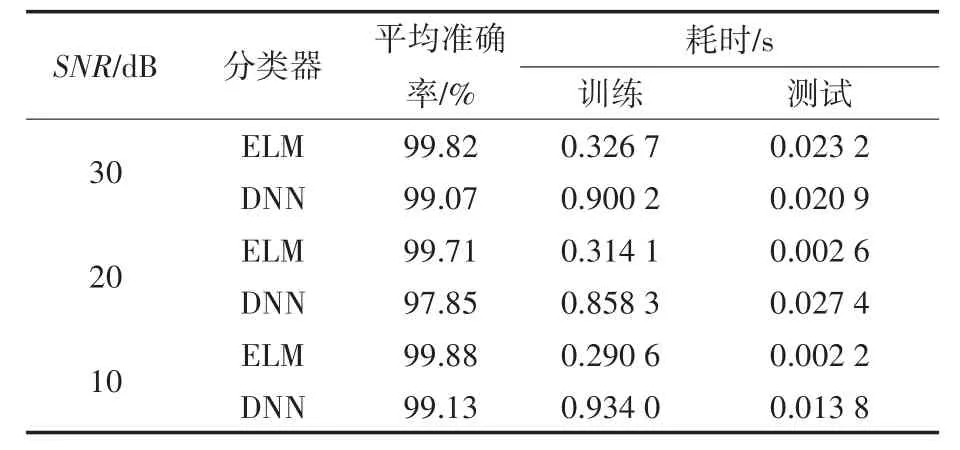
表1 不同信噪比下的准确率比较Tab.1 Comparison of accuracy under different SNR

实验同时分析了各个维度的特征对于模型分类过程的贡献。在每个类别中随机挑选100个样本并按类别依此排列，即第1类占据第1到第100个样本，第2类占据第101到第200个样本，等等。图7显示了8个维度的小波-熵特征在各个类别上的变化，图中的EC1～EC6分别指6个类别，依次为普通，暂降，暂升，谐波，中断与闪变。

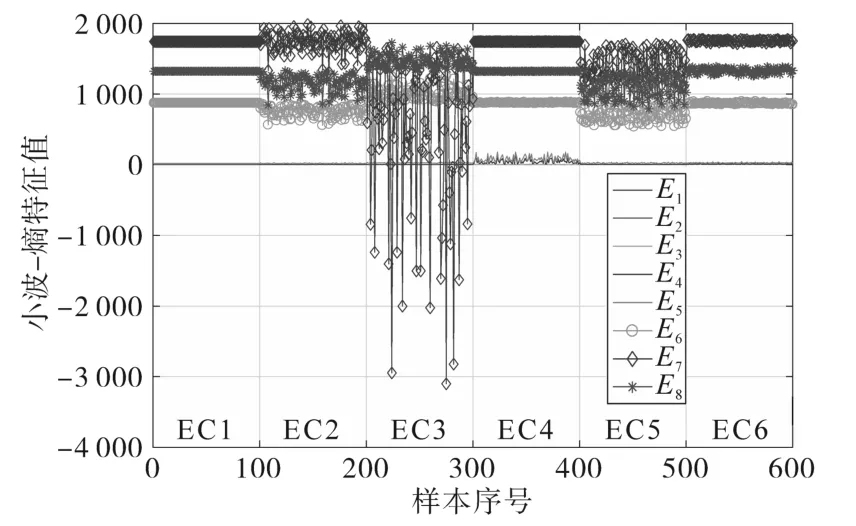
图7 小波-熵特征在不同类别样本上的变化Fig.7 Variation of DWT-entropy features on samples of different classes

从图7中可以看出，与E6～E8相比，特征E1～E5值接近0，且变化不明显，仅对EC4类别有微小响应，表2给出的使用不同特征子集时的模型性能验证了这一现象。可以看出，由于E6～E8特征在各个类别的PQE上差异较大，波形变化明显（E7最为显著），因此仅仅基于E6～E8就可以使分类模型达到较高的准确性，特征E1～E5在结合E6～E8后，特征集对PQE的分辨力也显著提升。

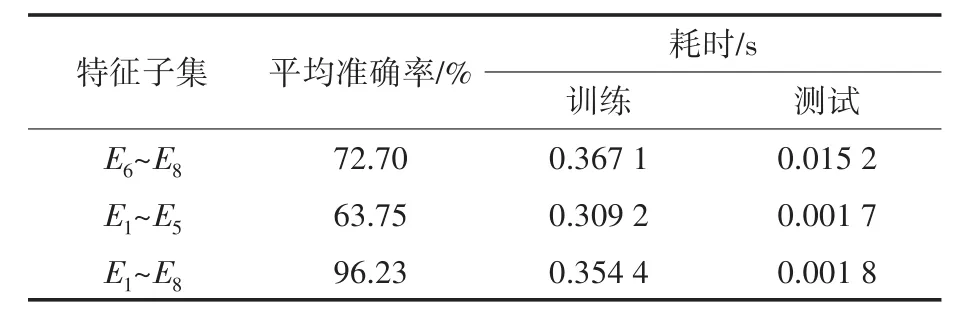
表2 不同小波-熵特征子集下的准确率比较（SNR=30 dB）Tab.2 Comparison of accuracy under different DWT-entropy feature subsets（SNR=30 dB）

表3进一步比较了小波-熵特征与直方图特征的重要性。两类特征提取方法在准确率上都较高，但小波变换所要求的计算量远大于直方图方法，因此特征提取耗时约为直方图方法的15倍。在实际应用场景中，需要综合准确率与效率两个方面的考虑。

表3 不同特征子集下的准确率比较（SNR=30 dB）Tab.3 Comparison of accuracy under different feature subsets（SNR=30 dB）

4 结论

本文提出了一种基于极限学习机的PQE分类器，结合小波-熵与直方图方法对PQE信号进行分类。利用其MRA特性，DWT方法适用于对PQE信号的多分辨率时频分析。通过引入熵，可以使降低数据维度并使信号特征更为显著。本文进一步引入直方图方法，在提取更为丰富的信号特征的同时，也可以大幅提升特征提取的效率，因此可用于嵌入式系统。在真实数据集上的实验表明，本文方法在分类准确率上达到了较高水平。通过进一步比较两类特征的重要性，可以指导实际应用场景下的特征选择。