钢筋混凝土框架梁柱子结构抗连续倒塌动力分析

2021-09-09张永兵刘泰奎

科学技术与工程 2021年22期

张永兵，刘泰奎，李治

(1.广西大学土木建筑工程学院，南宁 530004； 2.工程防灾与结构安全教育部重点实验室, 南宁 530004；3.广西防灾减灾与工程安全重点实验室，南宁 530004； 4.桂林理工大学土木建筑工程学院，桂林 541004)

1968年伦敦Ronan Point公寓的倒塌首次引起了各界学者对于连续性倒塌的注意，而1995年美国莫拉联邦大楼倒塌和2001年纽约世贸中心双子塔倒塌则使连续性倒塌问题成为学术界和工程界的一个热点问题。连续性倒塌[1]指由于结构遭受意外事件引起的局部破坏和局部损伤，通过结构破坏的连续传递，最终造成结构不成比例的坍塌。

近年来，中外学者在研究结构的连续性倒塌问题方面做了大量的工作。Sasani[2]进行对建筑物的原位去柱试验研究。研究表明：空腹桁架效应是影响结构倒塌过程中内力重分布的一个重要机制。Yu等[3-5]对一系列1/2缩尺中柱失效下的梁柱子结构进行了抗倒塌性能研究。研究表明梁柱子结构在试验过程中经历了弯曲效应阶段、压拱效应阶段、悬链线效应阶段，并证实了转动约束、跨高比、配筋率对结构破坏的影响。李易等[6]在总结国内关于混凝土框架结构抗连续性倒塌设计规范的基础上，提出了不同的抗连续性倒塌设计思想和设计方法。易伟建等[7]和李易等[8-9]通过非线性拆除构件法对现有的钢混框架结构进行了抗连续性倒塌性能方面的研究，并基于能量方法对钢混框架结构的连续性倒塌抗力需求分析讨论了梁机制和悬链线机制下结构抗连续倒塌的内力需求关系。何庆锋等[10]进行了5组约束梁的实验，通过改变配筋率、钢筋强度、加载速度等方式研究了梁柱子结构柱失效情况下考虑悬索效应对结构抗连续倒塌性能的影响。研究表明：钢筋的均匀拉伸和强度等级是影响结构抗连续倒塌性能的重要因素。

上述学者通过试验对拟静力加载条件下的钢混框架的抗连续倒塌的破坏机制和影响因素进行了大量的研究。但是目前中外学者在拟动力加载情况下的钢混框架结构的性能影响不足。肖宇哲等[11]通过对钢混梁柱子结构进行1次静力加载和4次动力加载试验，研究了钢混梁柱子结构的动力响应和动力连续倒塌。试验表明：动力损伤和材料应变率分别对梁机制动力效应和悬链线机制动力效应有重要的影响。罗维刚等[12]过基于清华大学的三层四跨框架拟静力倒塌试验建立了有限元模型，验证了楼板在结构抗连续倒塌设计中的作用不容忽视，同时对比了不同的拆柱时间对剩余结构动力响应幅值的影响。现基于已经完成的拟静力试验，运用ANSYS/LS-DYNA软件先建立精细化的模型[13-16]，再验证其于拟静力加载试验的准确性，最后再通过瞬时去柱的方式进行拟动力加载下的钢筋混凝土梁柱子结构动力响应分析。

1 试验概况

Deng等[17]采用拟静力加载方式研究了6个不同跨长、不同混凝土强度的梁柱子结构的抗连续倒塌性能。由于Deng等[17]所采用的试件数量较多，本研究仅选取其中的NSC-8试件和HSC-8试件进行研究。试件的钢筋构造如图1所示。其中NSC-8试件选用C45混凝土，HSC-8试件选用C80混凝土，两个试件的其余参数均相同。测得NSC-8试件的混凝土平均抗压强度为31.7 MPa，HSC-8混凝土的平均抗压强度为60.5 MPa。钢筋的力学性能如表1所示。试验装置如图2所示。

A-A、b-b、C-C和D-D为截面编号；@100表示箍筋间距为100 mm

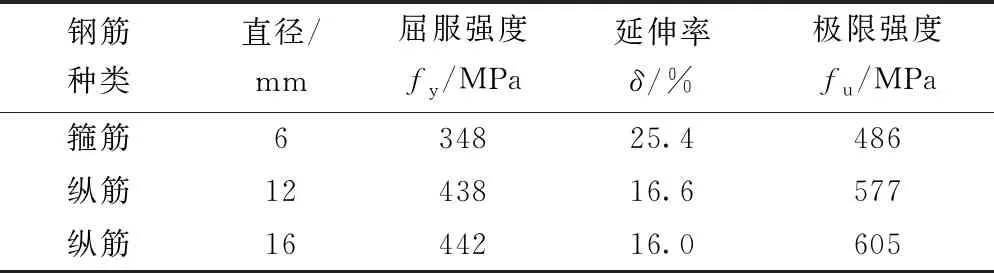
表1 钢筋材性[17]

图2 试验装置[17]

2 有限元模型建立

2.1 单元选取

采用有限元软件ANSYS/LS-DYNA进行有限元模拟。试验中试件由混凝土、钢筋和钢板组成,其中混凝土和钢板采Solid164实体单元进行模拟，钢筋采用Beam161单元进行模拟。

2.2 材料模型选取

有限元模型中的混凝土材料本构模型采用ANSYS/LSDYNA软件中的CSCM模型,其关键字为*MAT_CSCM(MAT_159)。CSCM模型的优点在于参数输入简单，只需输入密度、抗压强度、最大骨料直径参数，部分参数为默认值存储在模型中,剩余其他参数可由计算自动产生,因此对试验测量参数要求低于其他本构模型。

钢筋材料采用本构模型MAT_024，模型关键字为*MAT_PIECEWISE-LINEAR-PLAST-ICITY。该材料达到屈服后硬化曲线由多线段组成。材料参数通过简单的密度、弹性模量、泊松比、屈服应力及有效应力应变曲线等参数共同定义。钢材的应变率效应为

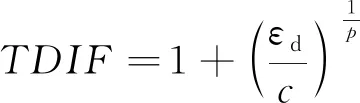
(1)

式(1)中：εd为钢筋的抗拉塑性应变；c和p为模型参数，通常情况下对于钢筋,取c=40，p=5。

加载和边界处所使用的钢板，则采用线弹性材料MAT-001(*MAT_ELASTIC)。

2.3 边界条件与有限元模型

由图2可以看出，试件在试验过程中均是通过螺栓同周围装置进行连接。精细化有限元模型为建立等效边界，将边柱螺栓用弹簧进行简化，弹簧单元用LS-DYNA中的*MAT_SPRING_ELASTIC(MAT_S01)，用关键字*CONSTRAINED_JOINT _SPHERICAL定义球铰来替代试件与底部支座相连处的螺栓。有限元模型边界条件如图3所示。有限元模型如图4所示。

图3 有限元模型边界条件

图4 有限元模型

3 有限元模型验证

3.1 荷载-位移曲线验证

将模拟所得的NSC-8试件的荷载-位移曲线与拟静力试验曲线进行对比。如图5(a)所示，可以看出在达到悬链线阶段峰值荷载之前，两者的变化趋势较为接近。试验压拱峰值位移为75.55 mm，有限元模拟压拱峰值位移为81.13 mm，两者相差7.4%；试验压拱峰值荷载为77.25 kN，模拟压拱峰值荷载为79.58 kN，两者相差3.1%；试验悬链线阶段峰值荷载为87.91 kN，模拟悬链线阶段峰值荷载为91.41 kN，两者相差3.8%。由此可以表明，该有限元模型各特征值吻合较好，发展趋势接近，能够较好地模拟试验的荷载-位移曲线。

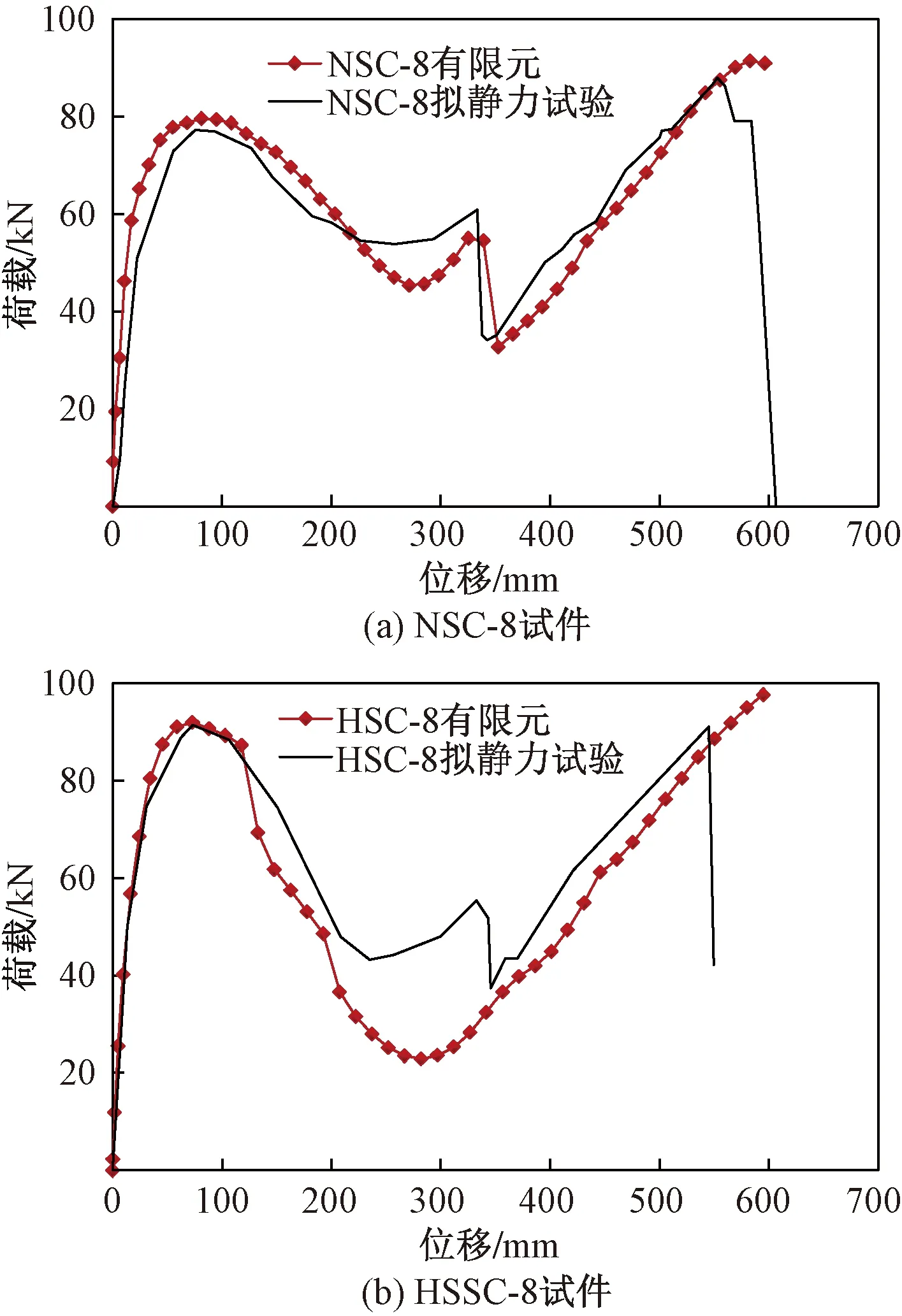
图5 有限元模拟与试验荷载-位移曲线对比

将模拟所得的HSC-8的荷载-位移曲线与试验曲线进行对比，如图5(b)所示，可以在达到压拱阶段峰值荷载之前，两者的变化趋势较为接近。试验压拱峰值位移为73.13 mm，模拟压拱峰值位移为73.21 mm，两者相差0.1%；试验压拱峰值荷载为91.50 kN，模拟压拱峰值荷载为92.21 kN，两者相差0.76%；试验悬链线阶段峰值荷载为91.15 kN，模拟悬链线阶段峰值荷载为97.13 kN，两者相差5.8%。表明该有限元模型各特征值吻合较好，发展趋势接近，能够较好地模拟试验的荷载-位移曲线。

3.2 破坏模态

NSC-8试件有限元破坏模态与试验破坏模态对比如图6所示。在竖向位移达到605.21 mm，外加荷载达到91.41 kN时，钢筋混凝土(RC)梁柱子结构中柱节点接近完全破坏，梁与中柱分离，结构抗力大幅度降低。如图6(c)所示，有限元局部破坏模态与试验局部破坏模态相似，梁柱节点处下部纵筋断裂。表明该有限元模型能够较好地模拟试验的破坏模态。

图6 NSC-8试件破坏模态[17]

HSC-8试件与NSC-8试件的破坏模式相似，有限元破坏模态与试验破坏模态对比如图7所示。在竖向位移达到599.56 mm，外加荷载达到92.21 kN时，RC梁柱子结构中柱节点接近完全破坏，梁与中柱分离，结构抗力大幅度降低。如图7(c)所示，有限元局部破坏模态与试验局部破坏模态相似，梁柱节点处纵筋发生断裂。表明该有限元模型能够较好地模拟试验的破坏模坏。

图7 HSC-8试件破坏模态[17]

4 动力响应分析

4.1 有限元模型建立

瞬间去柱模型如图8所示，为了模拟去柱前的工况，动力加载模型在失效柱的下方加有一个短柱。模型失效柱上方在计算过程中施加恒定荷载，通过关键字*MAT_ADD_EROSION定义附加破坏准则，并将失效时间设置为0.2 s，使计算时间进行到0.2 s时瞬时去除失效柱下方的短柱，以此模拟瞬时去柱。计算总时长设置为1.5 s，以确保结构振动稳定。

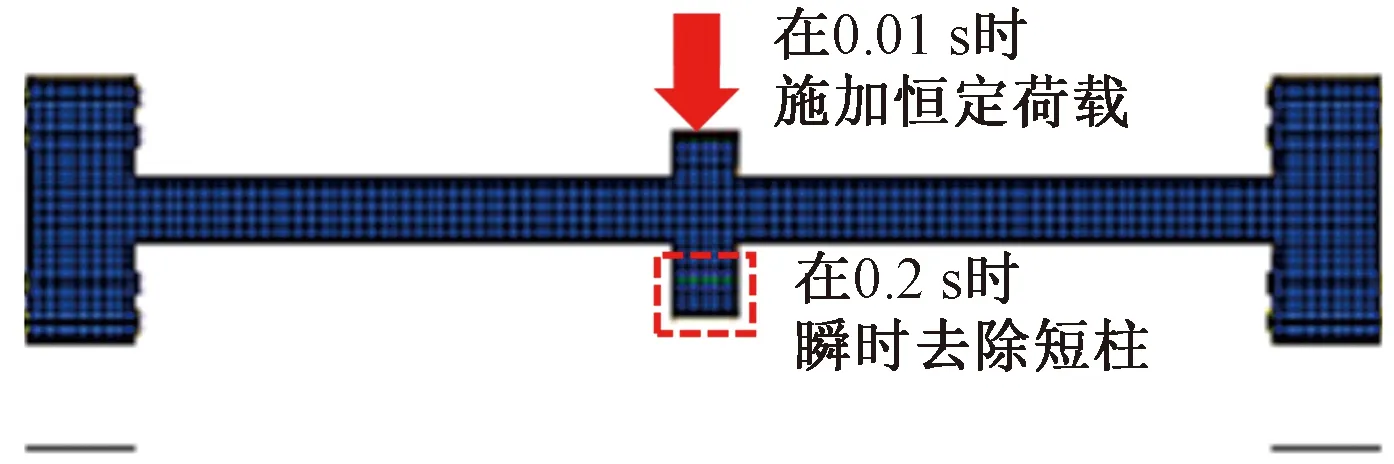
图8 瞬间去柱有限元模型

4.2 NSC-8试件动力响应

图9(a)为NSC-8试件有限元模型在外加荷载为30 kN时的时间-位移曲线，其中失效柱最大振幅依次为1.98、1.84、1.59、1.34 mm逐渐衰减，相邻峰值时间间隔依次为0.053、0.054、0.056、0.057 s。由此反映出结构在振动过程中自振周期增加，阻尼比减小。失效柱的最大振幅及基线位移分别占模型跨度的0.099%与0.51%，最大振幅占基线位移的19.4%。

图9(b)为NSC-8试件有限元模型在外加荷载P为60 kN时的时间-位移曲线，其中失效柱最大振幅依次为3.75、3.09、2.54、1.97 mm逐渐衰减，相邻峰值时间间隔依次为0.054、0.055、0.056、0.058 s。由此反映出结构在振动过程中自振周期增加，阻尼比减小。失效柱的最大振幅及基线位移分别占模型跨度的0.188%与2.24%，最大振幅占基线位移的8.39%。

图9 时间-位移曲线

图10为NSC-8试件有限元模型在动力荷载P=75 kN的时间-位移曲线。由图10可知，由于试件完全断裂，失效柱位移不收敛。

图10 试件破坏的时间-位移曲线(P=75 kN)

由图11可知，NSC-8试件有限元模型的破坏类与拟静力加载破坏形态不同。模型破坏是由于梁与边柱节点处形成贯通裂缝，纵筋断裂，梁与边柱分离，结构承载能力丧失。

图12为NSC-8试件有限元模型在不同外加荷载下的时间-位移曲线，其可以反映在不同动力荷载情况下模型的位移情况。如图12所示，当外加荷载由10 kN增加到70 kN时，动力位移从1.72 mm增加到93.12 mm。当外加荷载大于70 kN后结构破坏，时间-位移曲线开始不收敛，因此将70 kN可作为有限元模型的动态极限承载力。

图12 有限元模型动力增长趋势

图13为NSC-8试件不同动力荷载下的最大位移所做的动力荷载-位移曲线，该图由图12中每个荷载对应的最大位移点得出。

图13 动力荷载-位移曲线

4.3 HSC-8试件动力响应

图14(a)为HSC-8试件有限元模型在外加荷载为30 kN时的时间-位移曲线，其中失效柱最大振幅依次为3.03、2.10、2.07、1.24 mm逐渐衰减，相邻峰值时间间隔依次为0.054、0.054、0.055、0.057 s。由此反映出结构在振动过程中自振周期增加，阻尼比减小。失效柱的最大振幅及基线位移分别占模型跨度的0.152%与0.516%，最大振幅占基线位移的29.4%。

图14(b)为HSC-8试件有限元模型在外加荷载为60 kN时的时间-位移曲线，其中失效柱最大振幅依次为4.17、3.85、3.10、2.69 mm逐渐衰减，相邻峰值时间间隔依次为0.053、0.055、0.056、0.057 s。由此反映出结构在振动过程中自振周期增加，阻尼比减小。失效柱的最大振幅及基线位移分别占模型跨度的0.208%与2.16%，最大振幅占基线位移的9.6%。

图14 时间-位移曲线

图15为HSC-8试件有限元模型在动力荷载P=80 kN的时间-位移曲线。由图15可知，由于试件完全断裂，失效柱位移不收敛。

图15 试件破坏的时间-位移曲线(P=80 kN)

由图16可知，HSC-8试件有限元模型的破坏形态与拟静力加载破坏形态不同。模型破坏是由于梁与边柱节点处完全破坏，纵筋断裂，梁与边柱分离，结构承载能力丧失。

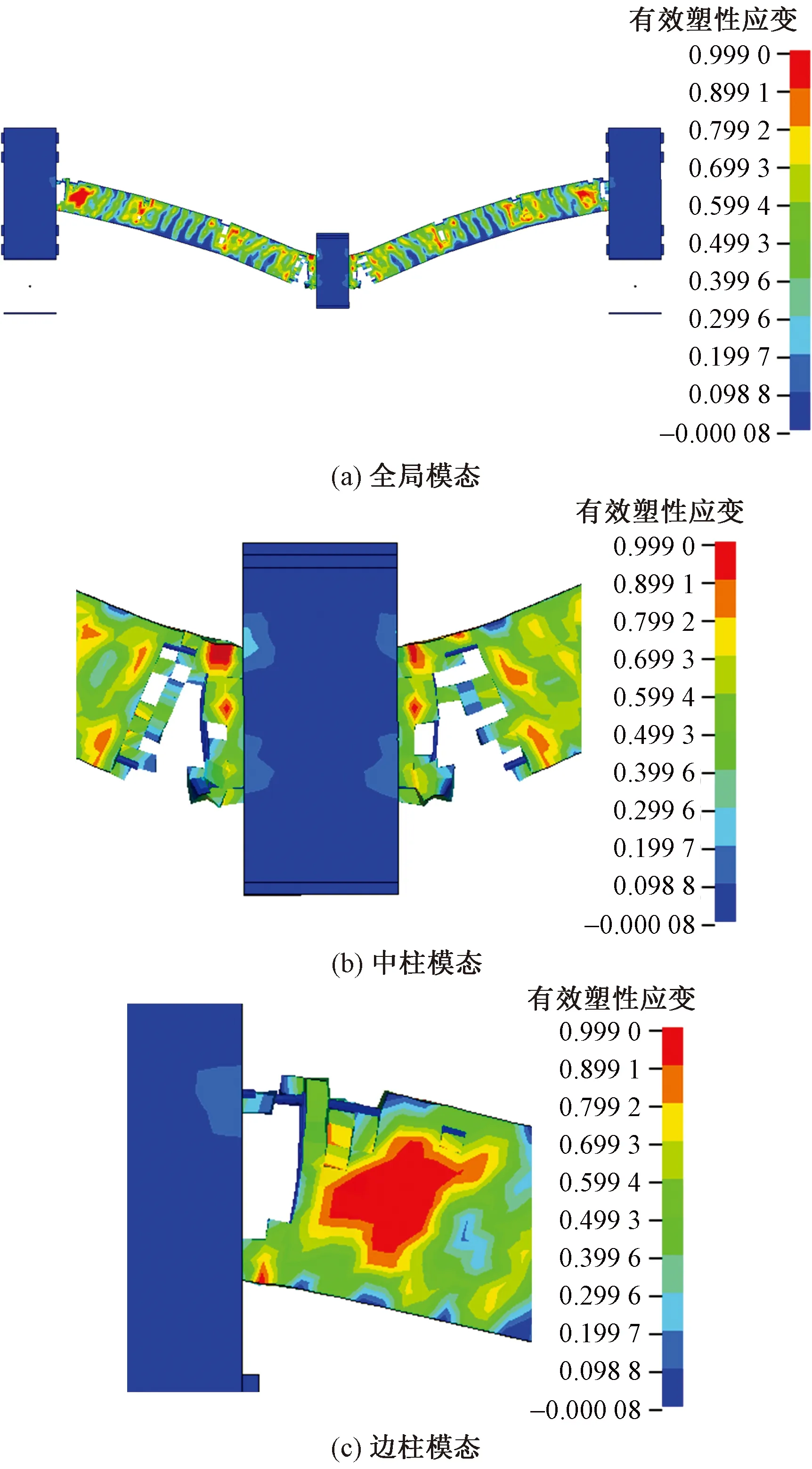
图16 动力破坏模态(P=80 kN)

图17为HSC-8试件有限元模型在不同外加荷载下的时间-位移曲线，其可以反映在不同动力荷载情况下模型的位移情况。如图13所示，当外加荷载由10 kN增加到75 kN时，动力位移从2.62 mm增加到110.23 mm。当外加荷载大于75 kN后结构破坏，时间-位移曲线开始不收敛，因此将75 kN可作为有限元模型的动态极限承载力。

图18为HSC-8试件不同动力荷载下的最大位移所做的动力荷载-位移曲线，该图由图17中每个荷载对应的最大位移点得出。

图17 有限元模型动力增长趋势

图18 动力荷载-位移曲线

4.4 基于能量法的动力分析

为了进一步研究RC梁柱子结构在瞬间动力去柱情况下的动力性能，采用能量法将静力荷载-位移曲线转化动力曲线，以便对RC梁柱子结构在瞬间动力去柱后的抗力进行预测。已有研究表明，能量法[18]可以方便地基于试验获得的拟静力荷载-位移曲线预测结构动力响应。能量法的基本数学表达式为

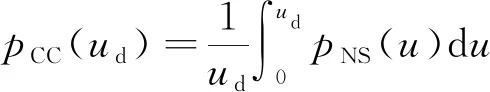
(2)

式(2)中：pCC(ud)和pNS(u)分别为极限承载能力和非线性静态加载结果；ud为极限位移；du为位移。

图19对比了NSC-8试件和HSC-8试件在能量法、有限元分析及拟静力试验得出的荷载-位移曲线。需要说明的是，由于试件在超过动态极限承载力时便已经完全破坏，时间-位移曲线不再收敛，所以有限元分析中在超过第一峰值荷载之后的荷载-位移曲线没有给出。可以看出，在相同位移下，试件的静态承载力总是大于动态承载力，动力变形能力小于静力变形能力。由于能量法中没有考虑结构阻尼效应的影响，导致能量法中所计算得出的动力承载能力曲线略低于有限元预测的动力抗力曲线。由于在数值模拟中可以考虑结构的阻尼效应，所以使得采用有限元模拟的方法比能量法所得出的结构动力荷载-位移曲线更加的接近实际情况。