热负荷作用面为圆形电器件散热器热阻数值分析
2021-09-09张金龙武振锋王良璧
卢 鑫,张金龙,武振锋,王良璧
(1. 兰州交通大学 机电工程学院,兰州 730070;2. 铁道车辆热工教育部重点实验室(兰州交通大学),兰州 730070)
肋片式散热器是工程中常见的一种设备,广泛应用于电子元件,制冷及工业冷却系统.散热器上的肋片增大了散热器与空气的接触面积,从而降低了风冷电子元件的热阻和工作温度,达到有效散热的目的.图1所示的肋片散热器是目前应用中最常见的一种结构,广泛应用在电子设备中的功率元器件,如晶闸管、集成电路等,它的结构是由平行的薄板以阵列的形式分布在基板上形成一系列矩形通道,热负荷作用面形状普遍为方形结构.
在实际工程应用中,从不同制造商提供的数百种型号的散热器中为特定设计选择最佳的散热器对工程设计者来说是一项比较艰巨的任务.最佳散热器的选择往往取决于其综合性能、尺寸参数、制造成本等多种因素.因此,为了权衡优化多方面的影响因素,需要设计者在选择过程的早期就能快速容易的预测散热器的性能.
许多国内外学者针对图1结构的肋片散热器散热特性进行了大量的理论分析与实验验证,并得出了许多重要的性能参数和通用性结论.图1结构散热器热源的作用面形状为方形,热量的传递方式首先从底板通过热传导的方式传递给肋片,再通过热对流和热辐射的形式散去.Muzychka和Yovanovich[1-3]提出了一种适用矩形截面散热器对流传热关联式.通过关联式可以求出矩形通道散热器的摩擦系数f,气流阻力R及流经整个散热器的气流压力损失,与传热学手册所提供的方法相比较而言,计算结果更接近于实验数据.Freegah[4]基于CFD数值模拟方法对新设计的半圆销型板翅式散热器强化传热进行了分析,在平行流和冲击流作用下比较了不同结构半圆销翅片的效率、基温和热阻,新结构设计为开发电子工业冷却系统提供很大的潜力.Prajapati[5]对不同翅片高度(0.4 mm~1.0 mm)的矩形并联微通道散热器的传热和流动特性进行了数值研究,发现翅片高度0.8 mm的传热效率最大.Jonsson[6]对七种不同结构散热片结构进行了综合研究,散热片包括板翅、直排式和交错式板翅,以及交错式的圆形和方形销形等.通过研究不同参数对散热器性能的影响,如风道高度、风道宽度、肋片的高度、厚度和肋片之间的距离等,得出了努塞尔数和无量纲压降的经验关联式.Huang等人[7]提出两种新型翅片散热器,即针型翅片和倾斜型翅片散热器,用于大功率LED灯在自然冷却条件下的散热,并对它们的散热性能进行了数值研究.研究结果表明,两种新型肋片结构散热器模型的总热阻与原模型相比降低了9.0%~15.6%,传热系数分别提高了12.6%~35.2%.
图1 阵列肋片式散热器结构 Fig.1 Radiator structure with fin array distribution
Castelan等人[8]建立了平板翅片散热器在强制对流冷却条件下的三维分析解模型,求解了散热器的平均温度和热阻,并与数值模拟进行了比较.分析模型与数值模型的平均温差(ΔT)最大差异为1.4 ℃.该分析解可用于优化设计,以减少现有散热器的重量,同时验证了该分析解用于优化冷却系统的快速性和精确性.赵亮等人[9]对采用数值模拟方法研究了电子器件冷却常用的平直翅片散热器及五种针翅散热器的散热性能,对比分析了不同来流速度下,不同散热器的热阻和流阻特性,得出相比于圆柱针翅、方柱针翅、75°斜柱针翅和60°斜柱针翅,45°斜柱针翅的热阻最小,但是其流阻增幅更大;增加针翅翅片的厚度能够有效降低热阻,但是其流阻增幅也更大;因此在针翅结构设计过程中,应选用较薄的方柱针翅、75°斜柱针翅或60°斜柱针翅结构.
综上所述,在电子元件肋片式散热器性能的研究中,国内外学者主要考虑的结构是热负荷作用面形状普遍为方形,且电子元件与散热器的相对关系大多数局限于图1所示关系.图2所示结构是一种应用于大功率整流柜散热结构,功率器件二极管热负荷作用面形状为圆形.对于图2所示热负荷作用面为圆形的研究很少.为此,本文将对热负荷作用面为圆形的电器件散热器散热性能进行研究,获得能快速预测散热器散热性能的结果,为此类散热器的结构优化提供指导.
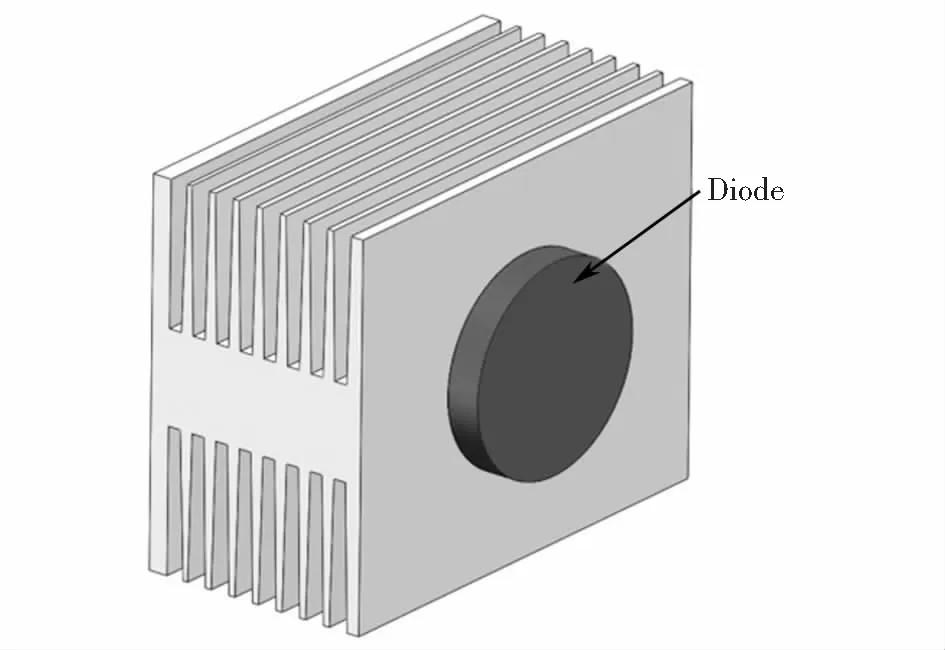
图2 二极管肋片式散热器三维简化模型Fig.2 A three-dimensional simplified model of diode- heated finned structure radiator
1 物理模型
1.1 几何模型
二极管肋片结构散热器几何参数如图3(a)~(b)所示,为了方便计算,将带有坡度的肋片厚度t和肋片间距b取平均值,散热器模型可以看做是由N-1个平行板通道组成.结构参数:翅片数n=9;肋片厚度t(t=3 mm),肋片间距b(b=5 mm),肋片高度d(d=46 mm),肋片长度L(L=140 mm),肋基厚度S(S=30 mm),散热器总高度W(W=71 mm),总宽度H(H=122 mm).散热器与二级管相接触的热负荷面定义为圆形C面,C面直径用D表示,在通道气体进口处指定均匀进口速度U和环境流体温度Tf.
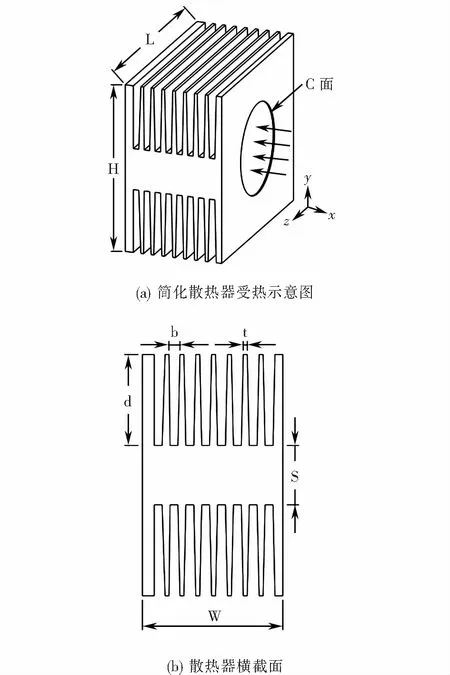
图3 二极管肋片式散热器几何参数Fig.3 Geometric parameters of radiator with diode heating fin structure
1.2 控制方程及边界条件
散热器固体区域的导热微分方程:
(1)
对于强制对流换热,辐射的热量比例很小,热量主要靠空气对流换热散发出去,因此,可忽略肋片的辐射换热,仅考虑其导热和强制对流换热.
C面上热边界条件
设二极管耗散功率PEH为常数,由导热第二类边界条件可得二极管与散热器接触面(圆形C面)处的边界条件为:
(2)
式中:Fc为二极管与肋基接触位置面积.
除C面以外面上热边界条件
(3)
式中:Tw为散热器壁面温度,Tf为环境温度.
1.3 热阻的定义
(4)
式中:Tmax为散热器最高温度.
2 对流换热系数的确定
要获得物理模型图3(a)的热阻,就得求解方程(1)~(3),在得到Tmax后就能得到Rf.要求解方程(1)~(3),先需获得表面对流传热系数h.下面我们介绍一下不求解流动方程获得该系数的方法.
2.1 边界层理论估计方法
传热学[10]中介绍了经典流体外掠平板层流分析解,雷诺数的定义为:
ReL=UL/ν.
(5)
如果假设肋通道可以用外掠平板近似,则物理模型图3(a)通道表面的对流传热表面传热系数近似为:
h=Nu·λ/L.
(6)
式中:L是肋片的全长,U进口风速(m/s),λ是流体导热系数,ν流体的运动粘度(m2/s).
2.2 修正边界层理论直接估计方法
Teertstra[11]等人将图1形式两个相同结构的散热器采取背对背的组合建立了分析模型,对平行平板开口通道中充分发展流动和发展流动两种极限情况模型分别进行理论求解并得出复合模型解,将肋效率考虑在内,得出了平均努塞尔数与散热器几何形状和流体速度的函数关系以及对强制对流冷却平板肋片开口通道散热器的平均换热率进行了预测.最后在不同的进风速度和发热功率的情况下对组合散热器模型进行风洞实验,将分析模型安装于紧凑的长方体的玻璃防护罩内以减小旁路效应,分析结果与实验结果非常吻合,最大误差为2.1%.
平均对流换热系数:
h=Nubλ/b.
(7)
平均努塞尔数:
Nub=Nui·η.
(8)
不考虑肋效率时的努塞尔数:
Nui=
(9)
肋效率:
(10)
通道修正雷诺数定义:
(11)
如假设初始环境温度为40 ℃,在1个大气压下干燥空气的物理参数如表1所示,并对计算进行对比分析.

表1 空气物性参数
当入口风速U=5 m/s时,ReL=41 273.6小于ReL=5×105层流过渡到湍流的临界值.因此,入口风速小于5 m/s时,符合流体外掠平板层流解特征数方程适用范围.进口风速为1 m/s、2 m/s、3 m/s、4 m/s、5 m/s时此类结构散热器的对流换热系数h计算结果如图4所示.
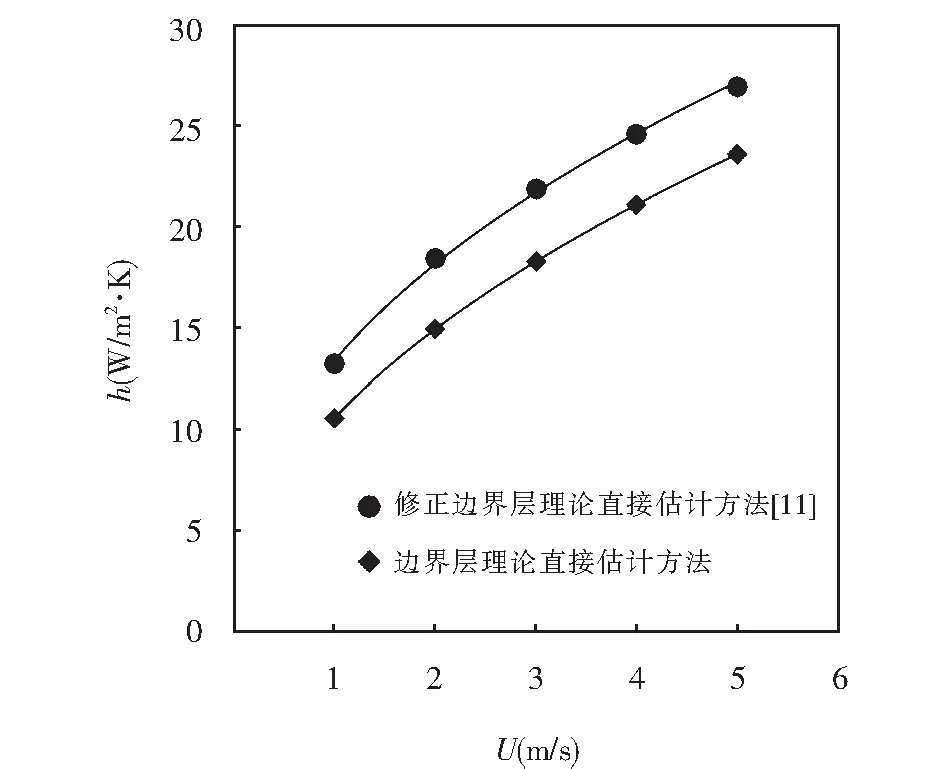
图4 入口风速对换热系数的影响Fig.4 Relation between inlet wind speed and heat transfer coefficient
由图4可以看出,两种计算方法所得表面传热系数变化趋势一致,最大绝对误差值为3.5 W/(m·K),最大相对误差为16%.由于对流换热系数的影响因素众多,散热器的几何结构因素是其中之一,将散热器开口通道结构近似为流体外掠平板进行求解是导致误差主要的原因.第二种方法针对肋片开口通道结构散热器,通过理论分析修正与实验验证,并且将肋效率考虑在内,比第一种估计方法要准确,从而论文使用第二种方法确定h.
3 数值方法
论文采用FLUENT 17.0软件进行模型方程(1)~(3)的三维数值模拟计算,为了确保计算结果的精确性,对数值模拟方法进行了网格独立性考核和可靠性分析.
3.1 网格独立性考核
网格的划分方式和类型将对数值模拟的精确解有一定的影响.合适的网格可以更准确地模拟散热器的热特性.论文采用多区域方法将整个几何形状离散为有限体积的六面体网格[12],如图5所示.
图5 肋片式散热器计算网格图Fig.5 Computational grid of a finned radiator
网格单元的数量对数值模拟的结果有很大的影响.为了保证数值计算的准确性,针对数值计算模型采用不同数量的网格进行了网格独立性考核:论文对加热功率为500 W,取入口风速U=5 m/s,对流换热系数值h=26.71 W/m2·K,初始温度T0=40 ℃,C圆直径D为66 mm的结构进行了网格独立性考核,其结果如表2所示.

表2 网格独立性考核
很明显所得结果准确性并没有随着网格元素数量的显著增加而显著提高,这说明使用1.84×106的网格已经能够获得网格独立的结果.
3.2 数值结果验证
为了确保数值结果的准确性,针对Ong等人[13]对图1所示结构,热负荷作用面形状为方形翅片散热器所报道的实验结果,论文采用与实验件相同结构尺寸的计算模型进行了数值模拟,数值结果与实验结果的比较如图6所示.
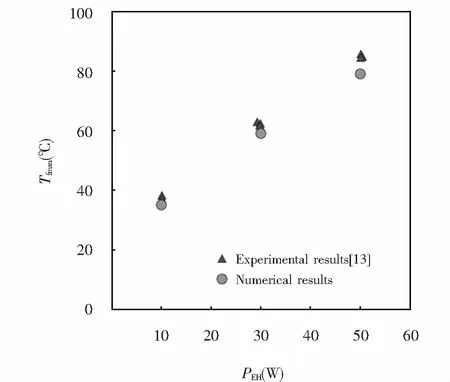
图6 数值计算结果可靠性验证Fig.6 Verification of the numerical results reliability
图6反映了三种输入功率PEH(10 W、30 W、50 W)的作用下散热器基板的最大温度Tfmax实验结果与数值计算结果.可以看出使用修正换热系数模拟计算的最大温度值与实验值吻合良好.为了提高实验的准确性,Ong等人在每一个输入功率PEH下,对实验重复进行三次,三次试验结果非常接近.不同功率PEH最大温度Tfmax的实验平均值与数值结果的最大相对误差为6.58%.可见论文中数值方法能获得可信的结果.
4 结果及分析
4.1 散热器温度分布
当散热器结构参数为n=9,t=3 mm,b=5 mm,d=46 mm,L=140 mm,W=71 mm,H=122 mm,C圆直径D=66 mm,散热器材料为铝,导热系数λ=202 W/(m·K),PEH=600 W,U=5 m/s时,热负荷作用面为圆形二极管散热器温度分布如图7所示.二极管直接作用在散热器顶板位置,与其他研究文献中热源作用在散热器基板位置不同,因此热量的传递方式也与其他肋片结构散热器有所不同.二极管产生的热量由顶板沿肋基和肋高方向逐层进行传递,越靠近顶板肋片温度越高.高温主要分布在与二极管接触的顶板肋片表面,最高温度主要出现在肋基的两端.如果最高温度超过器件的节温,器件失效.因此,掌握该类型结构散热器温度分布,对设计者来说,在已知功率器件功率和温度允许范围内,对散热器结构以及数量的选择有一定的参考意义,使得所选用的散热器在规定范围内不容易失效.
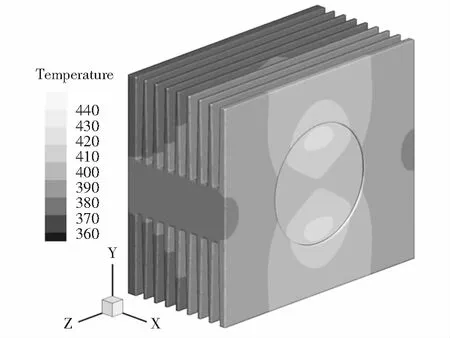
图7 热负荷作用面为圆形二极管散热器温度分布Fig.7 Temperature distribution of a diode radiator with a circular thermal load acting surface
4.2 Re对热阻的影响
设定环境温度为40 ℃,用前述散热器结构及材质,当二极管输入功率PEH分别为400 W、500 W、600 W时对不同风速U(即不同雷诺数Re)条件下对散热器散温度场进行分析.所得Re和Rf的关系如图8所示.由图8可以看出,随着Re的不断增大,三组不同输入功率PEH作用下的热阻Rf曲线走势一致,均以一定的规律逐渐减小,Re相同时,不同的输入功率PEH,热阻Rf值相等.
4.3 散热器材质导热系数对热阻的影响
设定环境温度为40 ℃,U=5 m/s,二极管输入功率PEH分别为400 W、500 W、600 W,散热器结构参数同前述,用不同材质的散热器进行温度场分析.所得导热系数λ和Rf的关系如图9所示.可以看出,散热器的热阻Rf随着材料导热系数的增大逐渐减小.
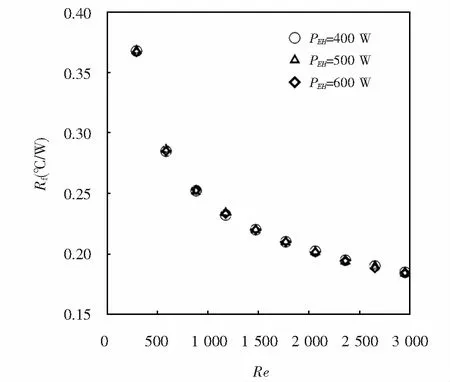
图8 雷诺数Re对热阻的影响Fig.8 Influence of Reynolds number on thermal resistance
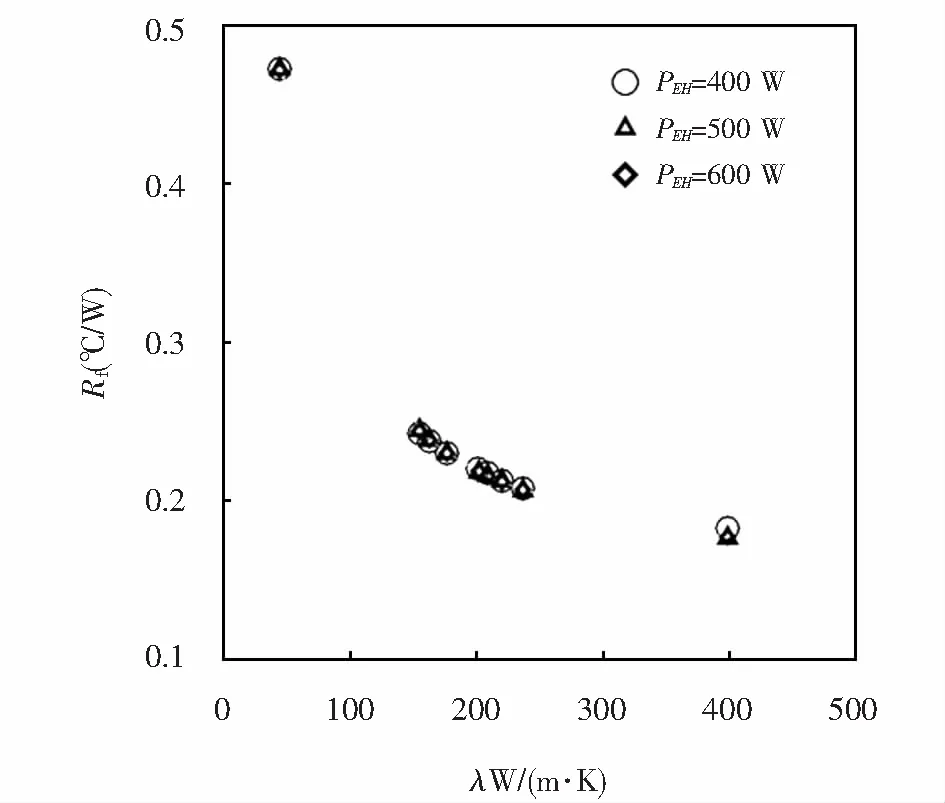
图9 导热系数λ对热阻的影响Fig.9 Influence of thermal conductivity on thermal resistance
4.4 热负荷作用面直径D对热阻的影响
散热器结构参数同前述,当二极管输入功率PEH分别为400 W、500 W、600 W,空气速度U=5 m/s(Re=1 474),改变热负荷作用C面直径D的尺寸对该结构散热器散热温度场分析,所得热阻如图10所示.可以看出,三种不同输入功率PEH作用下,随着热负荷作用C面直径D的增大,散热器热阻的变化趋势基本一致.当热负荷作用C面的直径D增加时,散热器热阻逐渐减小并趋于稳定,但随着C面直径D继续增加,热阻又不断增大.当C面直径D等于60 mm左右,热阻值达到最小.说明当热源通过热传导的形式将热量传递给散热器时,需要考虑热源与散热器的接触面积,接触面积大小不同时会导致导热热阻的变化.
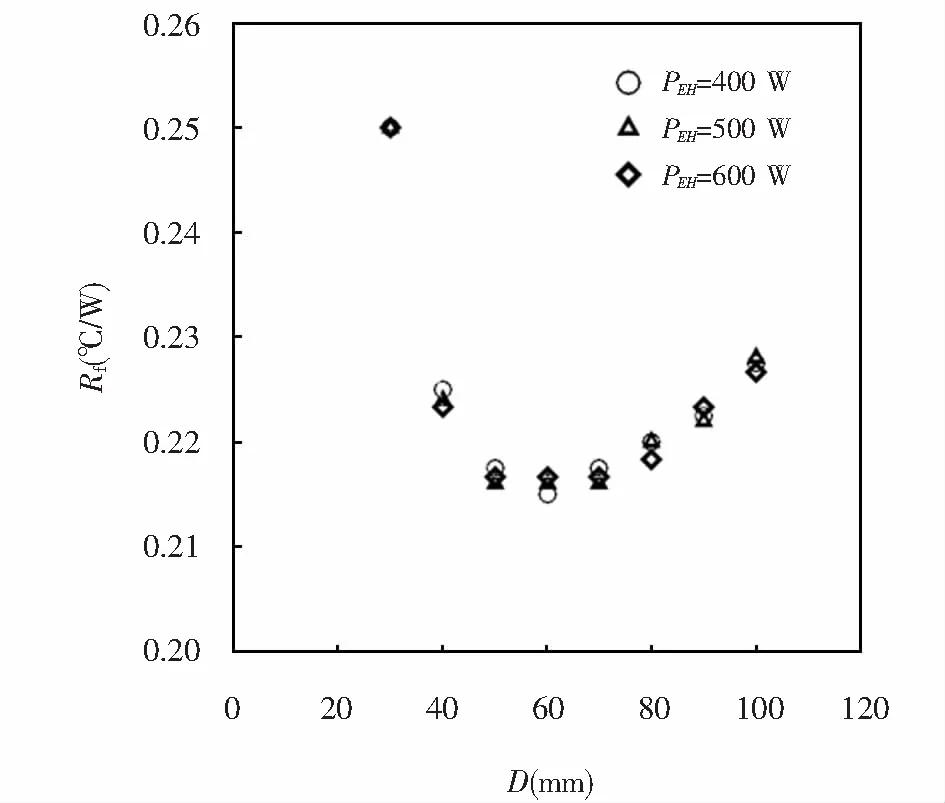
图10 热负荷作用C面直径D对热阻的影响Fig.10 Influence of thermal load surface diameter D on thermal resistance
图1所示为常见的散热器结构,其热量传递方向只沿着肋高方向传递.文献[14]中对这一结构散热器接触面积对热阻的影响进行了研究,得出结论:热负荷作用面面积与肋片基板面积相等时热阻值最小.然而本文所研究的散热器结构热负荷作用在肋片基板的一侧(作用在肋片顶板),热量的传递方向是先从顶板开始传递,同时沿着肋基方向,再沿着肋高方向进行传递.热负荷作用C面面积的大小除了和肋片顶板面积有关之外,更多的和肋基的厚度S有关.计算可得,对于论文中这一结构类型的散热器,肋基的厚度S与热负荷作用C面的直径D的比值等于0.5,即S/D=0.5时,热量可有效的沿肋基和肋高方向传递进行散热,热阻值达到最小.
4.5 热负荷对热阻的影响
图8~10表明,C面上加热功率PEH与热阻关联度不大.这主要是在计算Nu时用了固定的特征温度即初始环境温度都设定为40 ℃.因此,在散热器结构参数固定不变的情况下,由式(9)~(13)可得其Nu保持不变.当加热功率PEH增大时,使得最大温度Tmax相应增大,但不改变其热阻的大小.在后续的设计计算中,可忽略热负荷作用面上加热功率PEH对热阻的影响.
5 结论
论文通过理论和数值方法分析了热负荷作用面为圆形电器件散热器散热特性,并且在已知散热器尺寸参数和来流风速的情况下,能够快速容易的预测散热器的对流传热系数、肋效率、表面温度分布以及散热器热阻.与大多数文献研究的热负荷作用面形状为方形的翅片散热器散热性能有所不同,本文中发热器件热负荷作用面形状为圆形,热量的传递方式由肋片顶板沿肋基和肋高方向逐层传递,而大多数文献中热量的传递是由基板传向肋高方向.论文结论可总结如下:
1) 求解工程对流传热问题时,对设计者而言,在选用类似肋片结构散热器时,根据Teertstra提出的试验关联式能够快速预测估计其散热效率和表面传热系数.
2) 热负荷作用面形状为圆形时,最高温度分布出现在加热区域肋基的两端.
3) 热阻Rf随着雷诺数Re和材料的导热系数λ增大而减小,热阻Rf与雷诺数Re存在唯一对应关系.
4) 热阻随着热负荷作用C面直径D的增加呈现先减小后增加的变化规律.研究表明,热负荷作用C面面积大小对导热热阻有较大影响.论文中的散热器结构,当肋基的厚度S与热负荷作用C面的直径D的比值等于0.5时,热量从顶板有效的沿肋基和肋高方向传递进行散热,热阻值达到最小.
