基于随机微分方程的高速列车轮对预防性维护模型分析
2021-09-09皇甫兰兰苏宏升
皇甫兰兰,苏宏升
(兰州交通大学 自动化与电气工程学院,兰州 730070)
高速列车具有的运行速度高、运载能力强、准点率高、节能环保等优势越来越受到人们的青睐.然而高速列车速度的提高和运载能力的加大,在方便人们出行的同时,也带来了一定的安全性问题和维修费用的增加.列车轮对是高速列车运行安全的重要部件之一,是保证其安全性和可靠性的根源.而影响列车轮对正常服役的最主要的因素是轮对的磨耗,因此研究和分析列车轮对的可靠性及磨耗状态维护具有重要的理论意义和工程应用价值.
国内外学者在对磨耗监测和预测方面开展了大量的研究工作.文献[1]提出了一种轮轨接触算法,使得轮轨法向接触更加准确,计算效率更高.文献[2]基于半赫兹接触和完全理论程序计算了磨耗深度的分布.文献[3]基于动力学开发了一套车轮磨耗的计算方法.文献[4]利用动力学软件与磨耗模型的交互计算实现了磨耗预测.文献[5]利用数理统计理论,提出一种轮对磨耗数据处理方法以及周期预测模型.文献[6]基于拟合函数提出了一种轮对磨耗预测函数模型.文献[7]建立了一种考虑轮对柔性的车轮-轨道相耦合的系统动力学模型,分析了车轮扁疤对轮对磨耗的影响.上述文献的研究多采用动力学模型来计算车轮磨耗的模型.
本文针对列车轮对磨耗的既有统计数据,提出一种基于随机微分方程的状态预防性维修模型.随机微分方程可以克服传统的常微方程存在确定性积分无法描述部件维修过程中的不确定性因素的缺点,它可以描述维修过程中存在的随机干扰因素[8].状态预防性维护属于事前维修,通过对设备状态的采集和监控,预测设备的状态发展趋势,在故障发生之前进行的一种维护活动[9-12].本文以高速列车轮对状态为研究对象,将随机微分方程应用到预防性维护活动中,建立轮对状态转移随机微分方程模型,该模型是由轮对状态和运行里程相结合的故障函数,以及外界干扰引起的轮对状态波动两部分组成,既考虑轮对的内部退化过程,又添加外界随机因素对其状态的干扰;并选取某高速列车轮对的磨耗状态监测数据,建立状态转化模型,进而预测轮对的预防性时刻及车轮璇修周期,与铁路检修部门实际制定的车轮璇修周期进行对比,验证本文所提方法是否有效.
1 随机微分方程理论描述
随机微分方程广泛用于描述物理、经济、金融等不确定动态行为,其一维随机微分方程形式[13]如下:
(1)
其中:x(t)(t∈[t0,T])为完全概率空间(Ω,F,P)上的一维随机状态变量,表示系统在时刻t所处的状态,Ω为所有子集构成的σ-域,F为Ω集合的一个事件域,P为事件域F发生的概率;b(x(t),t)为漂移系数,σ(x(t),t)为扩散系数,b(x(t),t)、σ(x(t),t)均是Borel可测的;B(t)是一维布朗过程,布朗(Brown)过程也称维纳(Wiener)过程,是实际应用中由随机因素引起的随机过程,一般可以近似地用布朗过程来描述,对于任意t≥0,该过程均服从正态分布.
引理1[13](强解存在唯一性)如果系数b(x(t),t)和σ(x(t),t)满足局部Lipschitz条件以及线性增长条件,即对于所有|x|、|y|≤Rn且0≤t≤T,存在一个常数K,有
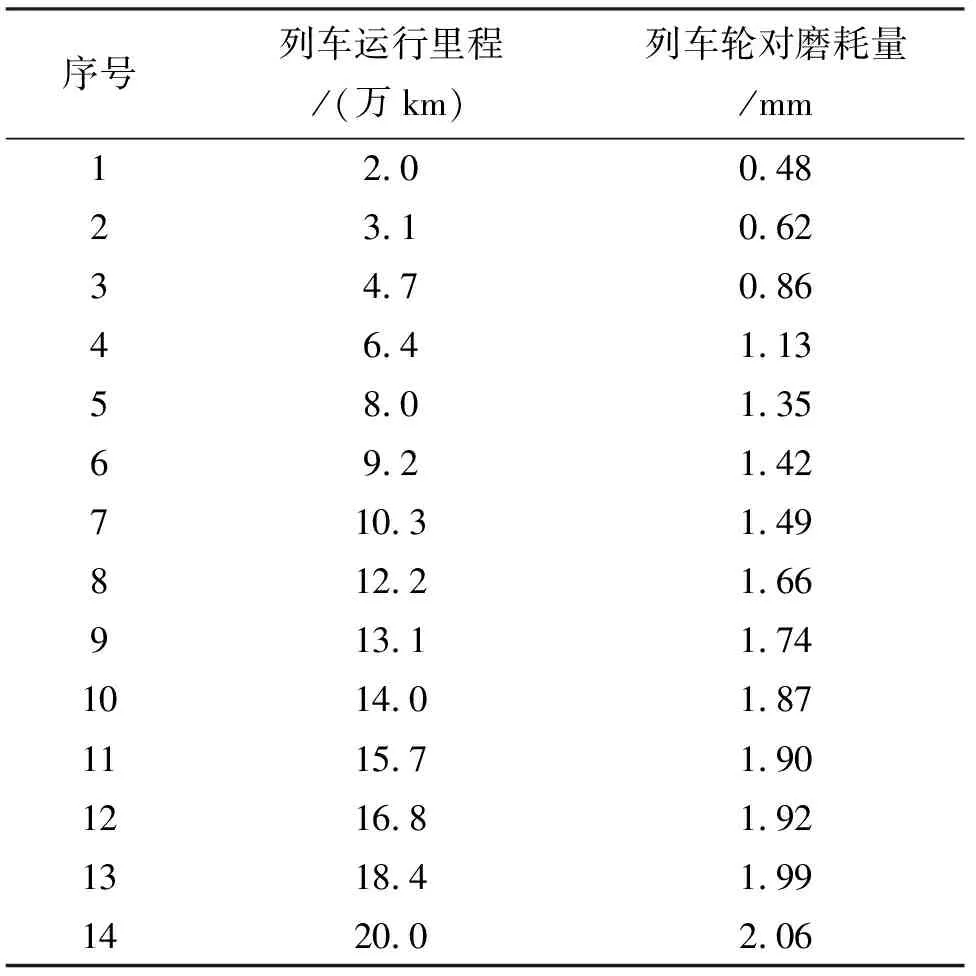
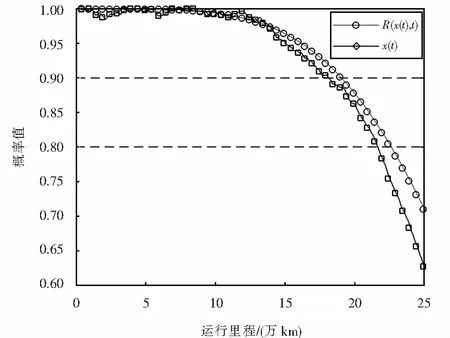
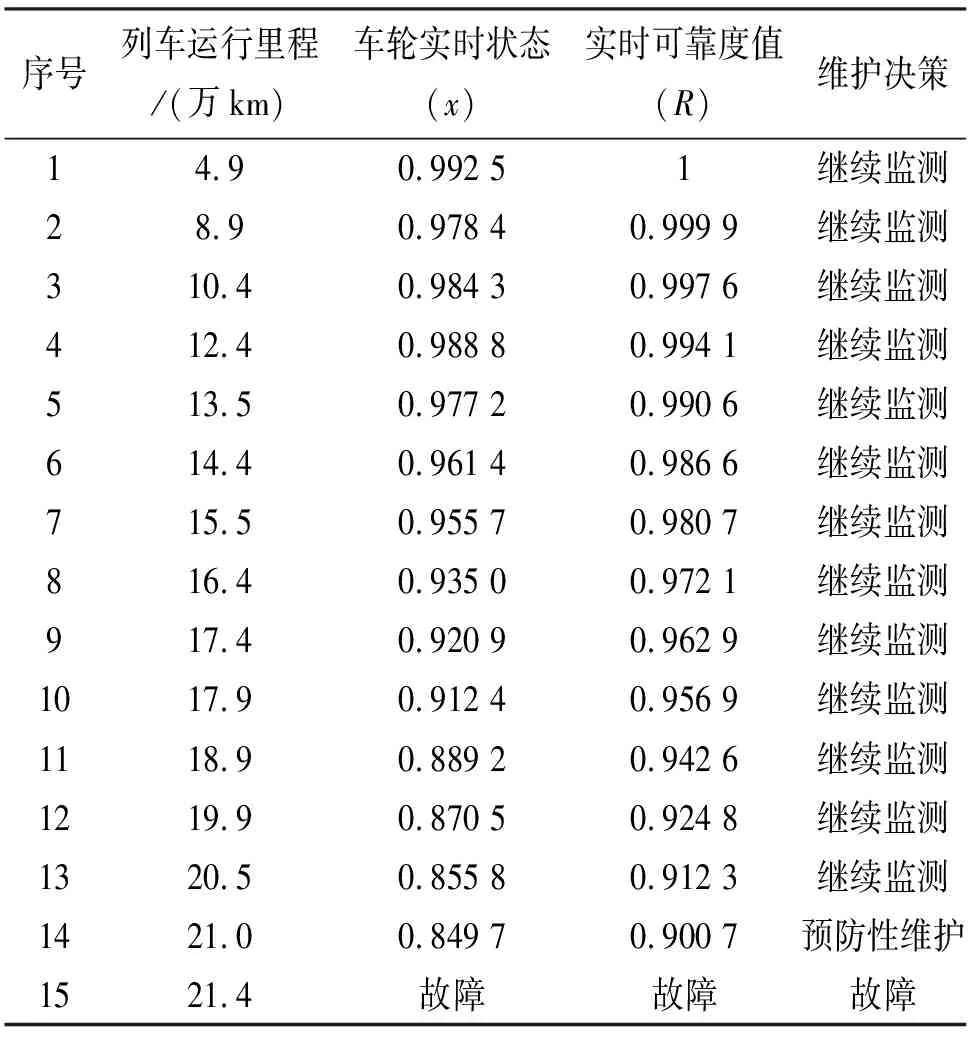
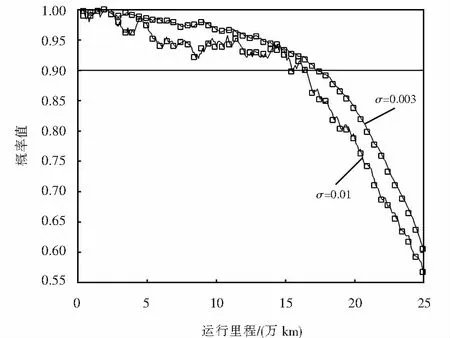
|b(x,t)-b(y,t)|+|σ(x,t)-σ(y,t)| (2) 且,存在常数KT,有 |b(x,t)|+|σ(x,t)| (3) 则,对于任意x(0)初值与布朗运动B无关,且满足E|x(0)|2<∞时,随机微分方程(1)存在唯一的强解且有连续的路径.同时满足条件 (4) 其中,C为仅与K和T有关的常数. 高速列车轮对状态的变化是由轮对本身的状态退化和外界随机干扰共同作用的结果,轮对本身的状态退化可以用故障率来表示,而外界的干扰是随机的.在建立高速列车轮对状态模型之前,本文作如下假设: 1) 轮对的状态检测认为是完美的,不存在无法检测的情况. 2) 外界随机干扰认为是在一个均值点附近随机波动,则干扰始终是独立和稳定的,且其期望值为0. 3) 轮对的故障与其状态、运行时间均相关. 基于以上假设条件,可建立基于随机微分方程(stochastic differential equation,SDE)的高速列车轮对状态模型: dx(t)=b(x(t),t)dt+σ(x(t),t)dB(t). (5) 根据可靠性理论中时间的定义,时间的概念通常是广义的,高速列车的时间评价尺度一般选用的是运行里程.因此,式(5)中:t表示的是高速列车的运行里程,单位为万km;x(t)表示高速列车轮对在时刻t的状态,当x(0)=1时,表示车轮在初始时刻处于全新状态,当x(t)=0时,表示车轮在时刻t处于完全损坏状态;b(x(t),t)称为漂移系数,是车轮的故障率;σ(x(t),t)为随机扰动系数,是车轮状态的波动率;B(t)是一维布朗过程. 当满足引理1时,该状态模型(5)具有唯一的强解. 高速列车轮对故障由时间和状态两个因素引起的,因此其故障率由基本故障率和状态相关的故障率两部分构成. 设备的基本故障率故障分布又称为寿命分布,常见的故障分布有指数分布、正态分布、伽马分布和威布尔分布,而威布尔分布在可靠性分析中应用的比较广泛,特别适用于机械中的疲劳强度、腐蚀寿命及磨损累计故障的分布形式[14].因此本文选用威布尔分布作为高速列车轮对的基本故障率,其表达式如下: (6) 式中:β为形状参数;η为尺度参数或特征寿命;t为高速列车的运行里程. 令轮对状态相关的故障率为g(x(t)),是一个在区间[0,1]上的有界可测实值连续函数,实际上它是RN维空间上的高速列车轮对状态x(t)映射在R1维空间[0,1]内的点.当x(t)=0时,表示车轮在时刻t处于完全损坏状态,则此时的故障率g(x(t))=1,因此可采用多项式进行逼近,其表达式可写为 (7) 由式(6)~(7)可求得高速列车轮对的故障率模型为 (8) 高速列车轮对所受的随机干扰是随机的,因此与列车的运行里程无关,即与时间t无关,但这种随机干扰对轮对的状态会产生影响,影响的强度记为σ,即状态波动的强度大小.则,波动率模型表达式可写为 σ(x(t),t)=σx(t). (9) 根据上述故障率和波动率模型,式(5)可写为 (10) 在高速列车轮对的状态监测中,轮对磨耗量是高速列车轮对的状态监测中的一个重要的特征量,与高速列车轮对的状态密切相关,本文选取轮对的磨耗量作为状态的观察指标.利用磨耗量的现场统计数据来估计状态模型的相关参数. 根据可靠性的基本知识,求得列车轮对状态模型的可靠度函数为 (11) 本文利用构造似然函数来进行参数β、η及a的估计,在构造似然函数之前,需求得参数β、η及a模型的概率密度函数为 从而可求得列车轮对状态模型的似然函数为 (12) 式中:n为采集轮对的磨耗量数据的个数;x(ti)为高速列车运行公里ti时的磨耗量. 对式(12)两边同时求对数,可得列车轮对状态模型的对数似然函数为 (13) 对式(13)求得一阶偏导方程组为: (14) 显然,令方程组(14)为0,没有显解,只能使用迭代法进行求解.本文采用牛顿-拉佛森(N-R算法)算法进行求解[15].令g为一阶偏导向量,则 (15) 求得二阶偏导方程组为: (16) 令H为二阶偏导向量,则H为 (17) 设当前的参数向量为 根据牛顿-拉佛森(N-R算法)算法,则下一个参数向量为 (18) 当k=0时,确定参数向量的初值,便可以通过迭代公式(18)求解最终的参数向量值. 本文选取某高速列车轮对的磨耗状态监测数据,见表1.根据现场实际数据统计,当高速列车运行里程达到20万km时,车轮的磨耗量大约达到2 mm,这时车轮的疲劳累计损伤值接近于1,表示列车车轮可能会发生疲劳破坏,这时不能保证列车正常运行. 表1 高速列车轮对的磨耗状态监测数据 根据3节模型参数估计方法,利用Matlab仿真软件对表1的高速列车轮对的磨耗状态监测数据进行仿真计算,可求得参数值为:β=4.44,η=323.49,a=0.1393.而波动率的大小选取σ=0.003.从而求得高速列车轮对状态转化模型为 0.003x(t)dB(t). (19) 高速列车轮对可靠性函数为 (20) 在Matlab仿真软件中对列车轮对状态转化模型(19)和可靠性函数(20)进行仿真,变化曲线如图1所示.从图1中的可靠性曲线可以看出,当可靠度取0.9时,高速列车能够安全运行的里程约19万km,另外,若可靠度值取0.8时,高速列车能够安全运行的里程约为23万km.为了更一步验证该模型的准确性,本文选取另外一组与上述型号相同的车轮磨耗数据,通过公式(19)计算出状态x(ti)实时值,并将该值带入式(20),从而求出可靠度达到阈值0.9时,高速列车的实际运行里程,进而确定车轮预防维护的最佳里程,即车轮的璇修周期.车轮可靠度及维护决策如表2所列,可以根据可靠性阈值0.9,最大限度的利用车轮的寿命,制定车轮的璇修周期21.0万km,这与铁路检修部门实际制定的车轮璇修周期20万km基本相符,说明模型的准确性.这样不但保障了高速列车的安全运行,同时在一定程度上降低了列车的运行成本. 图1 列车轮对状态函数和可靠性函数曲线图Fig.1 Train wheelset condition function and reliability function curve 表2 高速列车轮对可靠度及预防性决策 从图1曲线中可以看出,高速列车轮对状态的变化不是一条光滑的曲线,而是一条上下波动的曲线,反映了外界随机扰动对轮对状态影响,这个影响的大小和波动强度有关.为了更加清楚的说明状态的变化和波动强度的关系,本文通过以下方法来求解波动强度σ.在预防性维护区间[0,T]内,令Δt为状态监测步长,n为一个预防性维护周期内的监测个数,Δxn(t)为一个监测步长中的状态变化量,根据式(10),可得 (21) 式(21)进一步求解可得 (22) 当步长Δt→0时,式(22)可写为 (23) 从式(23)可以看出,波动强度σ和状态变化量Δxn(t)成正比,波动强度越大,状态变化量越大.为了验证式(23),在Matlab仿真软件中对波动强度的不同值进行仿真,不同波动强度下高速列车轮对状态的变化如图2所示.从图2中可以看出,波动强度越大,外界随机扰动对轮对状态影响越大,状态退化的速度越快,这与式(23)中反映的关系相一致. 图2 不同波动强度下列车轮对状态函数曲线变化图Fig.2 Wheelset condition function curve under different fluctuation intensity 1) 本文以某高速列车轮对的磨耗状态为研究对象,建立了列车轮对状态转化模型及可靠性函数模型,通过算例仿真分析,确定轮对的最佳璇修周期,与现场实际的璇修周期基本相符,验证了模型的有效性.与传统的固定璇修周期相比较,该模型能够反映轮对的实时磨耗状态,避免了轮对的欠维护和过维护. 2) 本文构建的列车轮对状态转化模型在一定程度上可以保障列车的安全运行以及成本的降低,为高速列车及其他行业中设备的维护决策提供一定的参考价值. 3) 本文在估算状态转化模型的参数时,仅依据了轮对的磨耗深度,考虑的不够全面,在后续研究中将探索影响轮对磨耗量的其他因素,使得建立的状态转化模型更加精确.2 高速列车轮对状态模型建立
2.1 故障率模型
2.2 波动率模型
3 高速列车轮对状态模型参数估计
4 算例分析
5 结论
