基于遗传算法的矢量磁测量非对准误差校正

罗建刚，张 峰，刘静晓，李海兵,2，罗 骋,2

(1.青岛海洋科学与技术试点国家实验室，山东 青岛 266237；2.北京航天控制仪器研究所，北京 100039)

0 引言

矢量磁测量技术是进行空间磁场测量和磁目标物探测的有效方法之一，与传统总场强度测量相比具有诸多优势[1-2]。矢量磁测量系统主要由三分量磁力仪和姿态仪构成，为避免姿态仪对磁力仪产生磁场干扰，通常将二者间隔一定距离放置并利用刚性结构件捷联安装；其直接测量结果为磁力仪坐标系下的三分量磁场和姿态仪坐标系相对于地理坐标系的姿态角(横滚角、俯仰角、航向角)，最终通过姿态坐标变换，得到地理坐标系下的矢量磁场信息[3]，实现动态条件下的矢量磁力测量。

理想情况下，三分量磁力仪和姿态仪坐标系处于对准状态，可将三分量磁场准确地变换至地理坐标系下；在实际工程中，三分量磁力仪坐标系和姿态仪坐标系均不可视，单纯依靠机械安装的方式难以保证二者坐标系精确对准，即存在非对准误差[4]。非对准误差会导致三分量磁场姿态坐标变换出现偏差，影响地理坐标系下矢量磁场的测量精度，为实现高精度矢量磁力测量，需要对非对准误差进行校正。文献[4]利用磁场/重力场在固定坐标系投影不变的原理校正三分量磁力仪和惯导的非对准误差，需要将磁力仪和惯导封装在正六面体内，另需借助高精度无磁直角台提供基准坐标系，当矢量磁测量系统体积较大时，此种方法并不适用；文献[5]利用3D Helmholtz线圈标定三轴磁传感器阵列间的非对准误差；文献[6]提出了一种车载三轴磁力仪安装误差的校准方法；文献[7—8]利用地磁矢量与重力矢量点积为常数的原理，对AHRS内部三轴磁强计和三轴加速度计的非对准误差进行校正；文献[9]为避免椭球拟合校正法的旋转模糊问题，利用POS算法校正地磁传感器和载体的安装误差，但实验测试中POS算法较椭球拟合法校正效果改善并不明显；文献[10]提出了一种标定电子罗盘与载体的安装误差的方法，但该方法仅能标定两个方向的误差角；文献[11—13]对三轴磁传感器的仪器误差进行了校正；文献[14—16]对惯导系统的误差进行了校正。上述文献或只针对单个传感器的误差进行校正，或提出的非对准误差校正方法针对特定系统且操作方法复杂，均不适用于常规意义上矢量磁测量系统的非对准误差校正。本文针对上述问题，提出了基于遗传算法的矢量磁测量非对准误差校正方法。

1 非对准误差分析与遗传算法

1.1 非对准误差分析

图1为矢量磁测量系统中坐标系示意图，其中XnYnZn为姿态仪本体坐标系，xgygzg为三分量磁力仪本体坐标系。为方便分析，将磁力仪本体坐标系xgygzg进行变换,得到中间坐标系XgYgZg，变换过程如式(1)所示，再将二者坐标系原点重叠放置，则矢量磁测量系统的非对准误差可表示为图2所示的形式。

图1 坐标系示意图Fig.1 Diagram of coordinate system

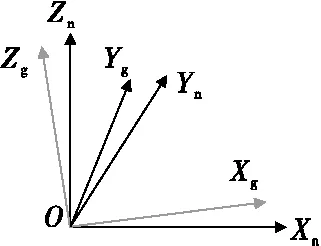
图2 非对准误差示意图Fig.2 Diagram ofmisalignment error

(1)

在进行非对准误差校正前，已分别对三分量磁力仪和姿态仪的自身误差进行了校正，可认为XnYnZn、XgYgZg均为正交坐标系；两个正交坐标系间任何复杂的角位置关系均可看作是有限次基本旋转的复合[17]，将三分量磁力仪坐标系XgYgZg进行有限次基本旋转，使之与姿态仪坐标系XnYnZn重合，则消除了非对准误差。

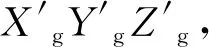
上述坐标系旋转过程可用式(2)进行表示：

Rn=CφCψCθRg

(2)

式(2)中，Rg表示磁力仪坐标系XgYgZg，Rn表示姿态仪坐标系XnYnZn，

通过上面的分析，把非对准误差校正问题转化为非对准角θ、ψ、φ的求取问题。

1.2 遗传算法

遗传算法(genetic algorithm,GA)是模拟生物在自然环境中的遗传和进化的过程而形成的自适应全局优化搜索算法[18-19]，通过对当前种群施加选择、交叉、变异等遗传操作，产生新一代种群，使种群逐步进化到包含或接近最优解的状态。

通过建立合适的目标函数，利用遗传算法优化计算可得到非对准角θ、ψ、φ的最优估计值。

2 基于遗传算法的非对准误差校正

2.1 遗传算法目标函数构建

在实际中，坐标系不可视，无法直接判断坐标系是否对准，但可以通过磁场矢量在二者坐标系的投影矢量进行判断。设bg=[bgx,bgy,bgz]T为三分量磁力仪的测量值，Bn=[Bnx,Bny,Bnz]T为磁场矢量在姿态仪坐标系的投影；令bg进行式(2)的坐标系旋转得到Bg=[Bgx,Bgy,Bgz]T，即：

Bg=CφCψCθbg

(3)

若有Bgx=Bnx，Bgy=Bny，Bgz=Bnz，则说明三分量磁力仪坐标系和姿态仪坐标系是重合的。

在地磁场环境纯净的区域，地理坐标系下的磁场矢量可以利用国际地磁参考场模型(IGRF)的计算值作为近似[4]，设Bd=[Bde,Bdn,Bdu]T为地理坐标系下的磁场矢量，根据姿态仪输出的姿态角信息，将Bd进行坐标系旋转，得到磁场矢量在姿态仪坐标系下的投影Bn=[Bnx,Bny,Bnz]T，旋转过程为：

Bn=CrCpChBd

(4)

式(4)中，

r、p、h分别表示姿态仪输出的横滚角、俯仰角和航向角。

令矢量磁测量系统在空间转动，尽量多的遍历空间姿态，三分量磁力仪的测量信息为bg(i)=[bgx(i),bgy(i),bgz(i)]T,(i=1,2,…,n)；姿态仪的测量信息为r(i)、p(i)、h(i), (i=1,2,…,n)。

根据式(3)、式(4)得到式(5)、式(6)：

(5)

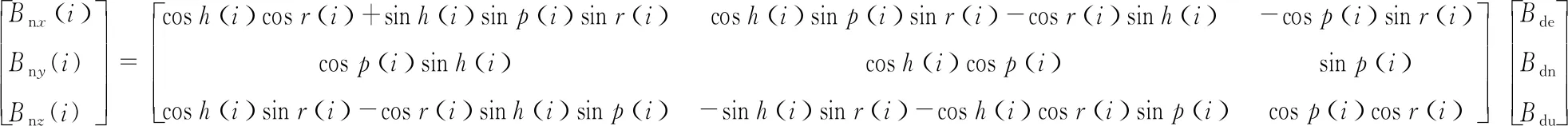
(6)

此时，如果有Bgx(i)=Bnx(i)，Bgy(i)=Bny(i)，Bgz(i)=Bnz(i)，(i=1,2,…,n)，则说明获得了θ、ψ、φ的准确值；但实际中，三分量磁力仪和姿态仪难免存在测量误差，可令：

令：

fθ,ψ,φ=(RMSx+RMSy+RMSz)/3

(7)

以式(7)作为遗传算法的目标函数，通过遗传进化使目标函数取最小值，即令：

fθ,ψ,φ=min,θ,ψ,φ∈R

(8)

2.2 基于遗传算法的非对准角估计

遗传算法估计非对准角的过程如下：

1) 以fθ,ψ,φ作为目标函数，θ、ψ、φ作为染色体基因；设定种群规模为NP、进化代数为G、交叉概率为Pc、变异概率为Pm；

2) 以实数编码方式对θ、ψ、φ进行编码，编码范围：[emin，emax]，随机生成NP个染色体的初始种群P(0)；

3) 个体评价：计算种群P(t)中各个染色体对应的适应度值fθ,ψ,φ(j)，(j=1,2,…,NP)，根据适应度值高低对染色体进行排序；

4) 选择、交叉和变异操作：根据Pc，利用最优染色体与种群中偶数位染色体交叉操作；根据Pm，进行变异操作产生子种群；

5) 个体再评价：将子种群与父种群合并，计算适应度值并对染色体排序，取前NP个染色体构成新种群P(t+1)，准备进行下一次遗传操作；

6) 终止条件判断：若达到最大进化代数G，则结束进化并输出最优染色体；否则，继续遗传进化。

通过遗传算法优化计算，可获得非对准角θ,ψ,φ的最佳估计值，然后根据式(2)对磁力仪坐标系进行旋转，即可实现非对准误差校正。

3 仿真分析与实验验证

3.1 仿真分析

为验证上述算法对非对准误差的校正效果，利用计算机进行仿真分析。设置环境磁场总场强度为50 000 nT，磁倾角为50°，磁偏角为-7°，计算得到地理坐标系下的磁场矢量Bd=[-3 916.8,31 899.8,-38 302.2]T。

模拟矢量磁测量系统在上述磁场环境中转动，采集三分量磁场信息和姿态角信息；设置如表1所示的矢量磁测量系统的非对准角；设置三分量磁力仪的测量噪声均值为0、方差为100 nT的高斯白噪声，姿态角的测量噪声均值为0、方差为0.002 5°的高斯白噪声。图4为三分量磁力仪输出的磁场分量曲线，图5为姿态角曲线。

图4 磁场分量曲线Fig.4 Magnetic field component curve

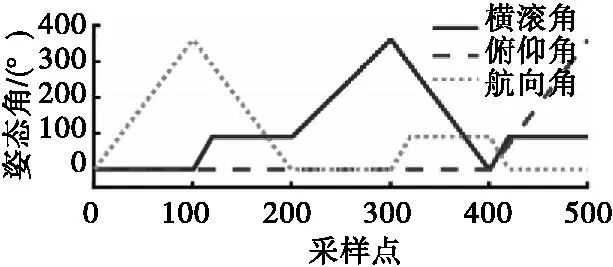
图5 姿态角曲线Fig.5 Attitude angle curve

利用上述遗传算法对非对准角进行估算，非对准角的计算值如表1，遗传算法的参数设置如表2。

表1 非对准角设定值与计算值对比

表2 遗传算法参数设置

从表1可见遗传算法对非对准角有很高的估算精度，根据估算出的非对准角，通过式(3)实现非对准误差校正。为方便对比，将非对准误差校正前后的三分量磁场数据分别变换至地理坐标系下，变换过程如式(9)、式(10)。

(9)

(10)

其中，

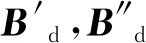
地理坐标系下各磁场分量曲线对比见图6。非对准误差校正前各分量曲线明显偏离真实值，具有较大的均方根误差；非对准误差校正后各分量曲线基本与真实值曲线重合，均方根误差显著减小。校正前后均方根误差对比见表3，校正后各分量均方根误差改善率在94%以上。通过仿真分析证明本文所提出的方法对非对准误差有良好的校正效果。

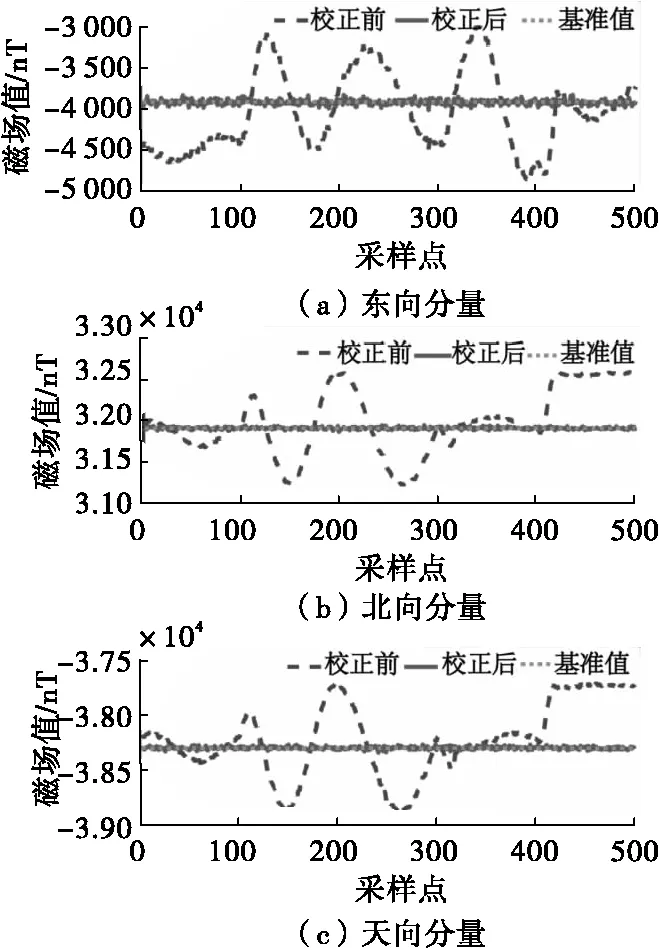
图6 地理坐标系下曲线对比Fig.6 Comparison of curves in geographical coordinate system

表3 均方根误差对比

3.2 实验验证

实验设备主要包括三分量磁力仪、高精度光纤惯导(姿态仪)、无磁刚性结构件、数据采集板、上位机、三轴无磁转台等。三分量磁力仪与光纤惯导通过无磁刚性结构件捷联安装构成矢量磁测量半实物系统，数据采集板与上位机负责采集与存储数据，系统部分组件如图7。

图7 矢量磁测量系统Fig.7 Diagram of vector magnetic measurement system

实验地点选择在青岛市周边某海岛上，实验地点远离磁干扰源，通过IGRF12模型计算出实验地点的东、北、天向磁场分量分别为：-4 185.3 nT，30 153.0 nT，-42 250.4 nT。

利用三轴无磁转台转动矢量磁测量系统并记录一组数据，图8为三分量磁力仪输出的磁场分量曲线，图9为光纤惯导输出的姿态角曲线。

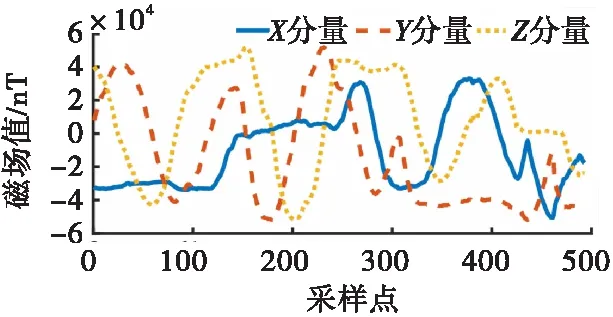
图8 磁场分量曲线Fig.8 Magnetic field component curve

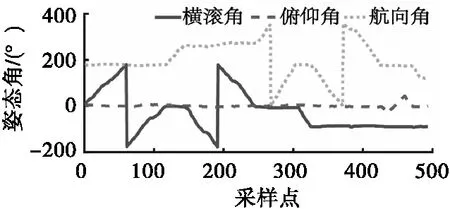
图9 姿态角曲线Fig.9 Attitude angle curve

利用上述遗传算法对非对准角进行估算，遗传算法参数设置同表2，非对准角的计算值见表4。通过式(3)进行非对准误差校正，然后根据式(9)、式(10)将校正前后的三分量磁数据分别变换至地理坐标系下，地理坐标系下各分量曲线对比见图10，校正前后各分量的均方根误差对比见表5。

表4 非对准角计算值

图10 地理坐标系下曲线对比Fig.10 Comparison of curves in geographical coordinate system

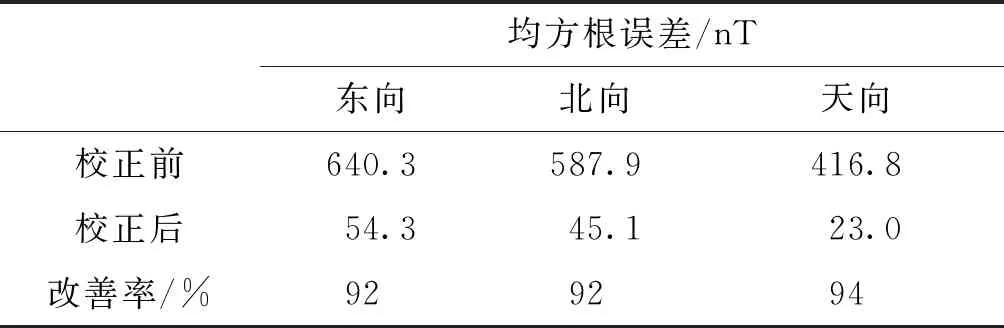
表5 均方根误差对比

对比上面曲线，非对准误差校正前，地理坐标系下各分量磁场曲线出现近2 000 nT的波动，说明非对准误差严重影响了矢量磁测量的精度；非对准误差校正后，地理坐标系下的各分量曲线更接近真实值曲线，明显提高了矢量磁测量精度；对比校正前后各分量的均方根误差，校正后各分量数据的改善率均在92%以上，说明上述方法对非对准误差起到了良好的校正效果。

4 结论

本文提出了基于遗传算法的矢量磁测量系统非对准误差校正方法，该方法以空间磁场的投影矢量为基准，通过三步坐标旋转的方式实现磁力仪和姿态仪坐标系对准，然后利用遗传算法估算其中的坐标系旋转角度(非对准角)，最终实现非对准误差校正。通过仿真计算和实验验证，该方法可以准确估算出非对准角，经非对准误差校正后，仿真数据和实测数据各分量的均方根误差改善效果分别在94%和92%以上。综合分析认为该方法具有一定工程应用价值。