基于正逆向导航解算的捷联罗经动基座对准研究

于飞飞，王振桓，曾庆双，陈希军

(哈尔滨工业大学航天学院，哈尔滨 150001)

0 引言

罗经系统典型的对准方法有解析对准和罗经法对准[1-4]。罗经法初始对准是利用罗经原理基于控制反馈的自主式对准方法[5]。罗经法对准不需要精确的数学模型和噪声模型，并且具有自主性强、精度高和航向误差不随时间积累等特点[6]。捷联罗经初始对准是基于罗经效应通过控制算法完成闭环调节的过程，对准算法的精确性和快速性是相互制约的。随着光纤陀螺、激光陀螺和加速度计等惯性器件的日益成熟完善，为捷联罗经初始对准研究增加了新的活力[7]，最终使精度得到了很大提高，而快速性问题逐步成为捷联罗经对准研究的主要问题之一。将逆向导航解算运用于捷联罗经对准之中，改进捷联罗经对准方法，对缩短其对准时间具有重要的现实意义[8]。严恭敏将逆向导航解算应用于捷联罗经初始对准中，设计了快速捷联罗经初始对准方法，并借助辅助外速，将正向捷联罗经初始对准与逆向航位推算相结合，实现了行进状态下的捷联罗经初始对准和位置导航[9]。目前进行的仿真或试验基本是在静止或直线运动条件下完成的，在实际应用中，很难达到这种理想状态。在动基座条件下，姿态角一直处于变化中，如果采用文献[9]中的方法，在导航计算机处理数据期间载体姿态角已经发生变化，计算完毕后并不能获得最新的姿态角；另外，还可能遇到较大干扰或恶劣环境，造成粗对准航向角误差变大，有时能超过10°以上，在大失准角条件下会延长精对准时间，尽管不影响最终精度，但快速性受到影响[10]。本文针对上述问题进行了深入研究，提出了基于姿态补偿的对准方法和正逆向二级变参数对准法，解决了相关问题。

1 捷联罗经初始对准原理

捷联罗经初始对准原理如下[11]：

水平对准东向通道

(1)

水平对准北向通道

(2)

罗经方位通道

(3)

K(s)=KU3/ωiecosL·(s+KU4)

(4)

2 捷联罗经回路参数分析

分析罗经回路参数的目的是通过配置合适的极点，提高对准回路系统的综合性能。

2.1 水平对准回路参数

根据水平对准通道方程，并以水平对准北向回路为例，进行对准回路分析。

设衰减系数为σ，σ=ξωn，无阻尼振荡频率为ωn，阻尼振荡频率为ωd，则特征根可设为：s1=-σ，s2=-σ+jωd，s3=-σ-jωd，构造特征多项式如下

Δs=(s+σ)(s+σ-jωd)(s+σ+jωd)

(5)

由回路方程求得水平对准北向回路特征多项式如下

(6)

2.2 方位对准回路参数

根据罗经方位通道方程，列写方位回路特征多项式如下

(7)

罗经方位回路中的KU1、KU2和水平对准北向回路中的KN1、KN2并不相同。显然，罗经方位对准回路是一个四阶系统，一般用2个二阶系统串联来实现，论文采用以下两种方式实现。

方法a，2个相同振荡环节串联，这是一种最经典的设置方法[12]，特征多项式为

(8)

对比式(7)和式(8)系数，可得参数如下：KU1=KU4=2σ，KU2=2σ2/(ξωs)2-1，KU3=σ4/(ξ4g)。

2个振荡环节，跟踪速度快，但不利于对准结果的稳定，在摇摆状态下对准时，对准误差较大。

方法b，1个振荡环节和1个过阻尼环节，极点配置有区别于方法a，此配置方法具有更强的跟踪能力，同时保证了稳态精度，能够提高摇摆状态下的对准精度[13]。特征多项式为

(9)

对比式(7)和式(9)系数，可得参数如下：KU1=2ωn，KU2=2σ2/(ξωs)2-1，KU3=σ4/(ξ4g)，KU4=2σ。

本文中水平对准参数设计均使用同一种设计思路，方位对准参数根据不同的载体状态，使用不同的配置方法。

2.3 调节参数Td

Td为阻尼振荡周期，在实现对准时以Td为调节参数更加方便直观。由前述分析可知，三阶水平对准回路和四阶方位对准回路均建立在二阶回路基础之上，因此从二阶系统入手分析Td作为调节参数的优势。

典型的二阶闭环传递函数为

(10)

取Td=30s，ξ=0.3，其单位阶跃响应曲线，如图1所示。

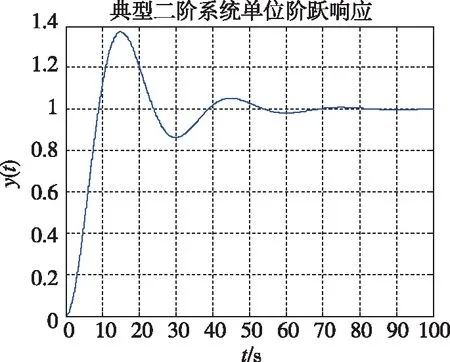
图1 典型二阶系统单位阶跃响应曲线Fig.1 Unit step response curve of the typical second-order system

将2个典型二阶系统串联起来获得典型四阶系统，Td和ξ保持不变，单位阶跃响应曲线如图2所示。

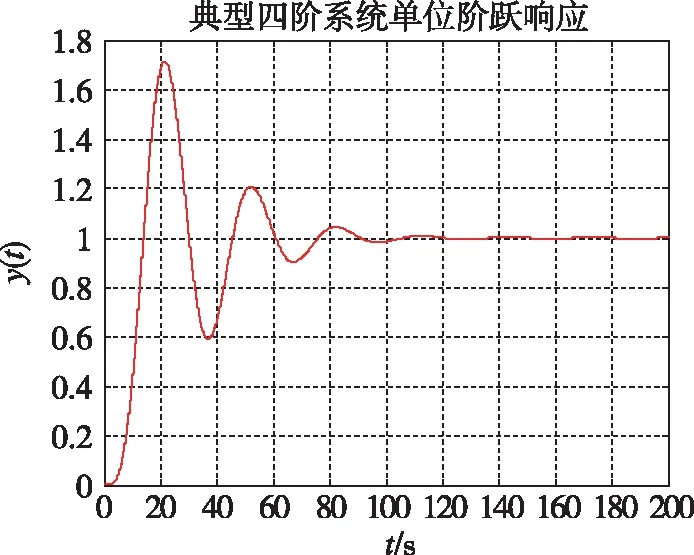
图2 典型四阶系统单位阶跃响应曲线Fig.2 Unit step response curve of the typical fourth-order system

在ξ一定时，对于二阶系统和四阶系统来说，Td可以反映tr、tp、ts等指标，振荡次数主要由ξ确定。因此，对于罗经法初始对准来说，在ξ一定时，以Td作为调节参数更加直观实用，可以在一定程度上反映对准时间；但在实际工程中，由于环境和器件误差等原因，Td不能选的太小，否则系统振荡加强，不利于稳定收敛。因此，在算法实现时可将水平对准回路和方位对准回路参数改写为以Td作为调节参数的形式。文中水平回路用Txy表示，方位回路用Tz表示。

3 逆向导航解算运用分析

由文献[9]可知，正、逆向导航算法在形式上是相同的，只要将正向存储的陀螺数据和地球自转角速率取反，并将正向终值设置为逆向初值，就能实现逆向导航。因此，在捷联罗经初始对准中，如果被逆向处理的数据作为一组新数据继续使用，等效增加了数据量；或者将正向罗经对准和逆向姿态解算相结合，正向反复使用数据，也可等效为增加了数据量[14]。逆向导航解算在捷联罗经初始对准中的运用主要有两种思路，具体如下：

全循环正逆向对准：初始对准完成一次粗、精对准后，将相应数据存储，并作逆向处理，构造一组新数据，接续进行逆向罗经精对准，进行精对准正逆向循环直到精度符合要求，时序如图3所示。

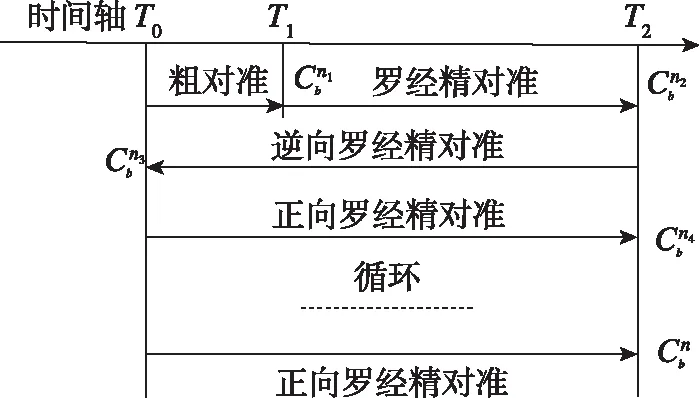
图3 全循环正逆向对准法时序图Fig.3 Sequence diagram of the full cycle forward and reverse alignment method

半循环正逆向对准：初始对准完成一次粗、精对准后，将相应数据存储，以获得姿态矩阵为初值，进行逆向姿态解算至起点，利用存储的数据，再次进行正向罗经精对准，如此循环直到精度符合要求，时序如图4所示。

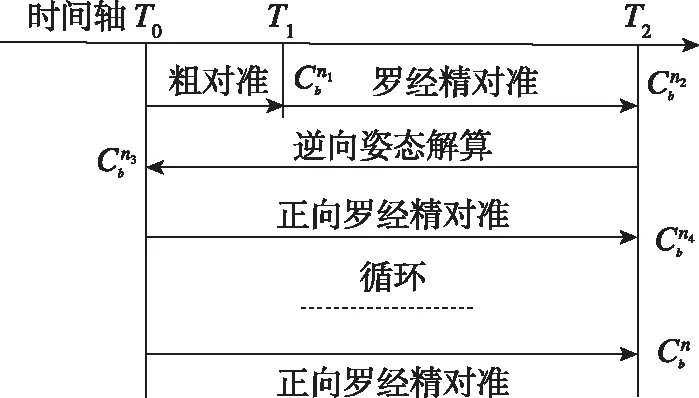
图4 半循环正逆向对准法时序图Fig.4 Sequence diagram of the half cycle forward and reverse alignment method

4 动基座逆向捷联罗经精对准算法

将方程组(1)～(3)离散化后，借鉴文献[9]的逆向导航推导思路，推导动基座逆向捷联罗经精对准算法，具体如下：

逆向水平对准东向通道

(11)

逆向水平对准北向通道

(12)

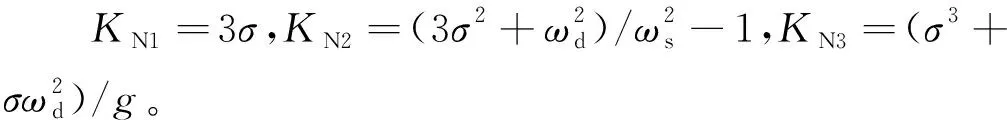
逆向罗经方位通道

(13)

参数为：KU1=KU4=2σ，KU2=2σ2/(ξωs)2-1，KU3=σ4/(ξ4g)。

如果是单纯的摇摆状态下，此时载体没有线运动，可将辅助外速置零，但是逆向罗经方位通道采用如下配置为：KU1=2ωn，KU2=2σ2/(ξωs)2-1，KU3=σ4/(ξ4g)，KU4=2σ。

5 基于姿态补偿的对准实现及仿真试验

5.1 姿态补偿分析

在动基座条件下，若姿态角在T2时刻后发生了变化，直接运用上述两种思路进行对准，对准结果会存在很大误差，无法完成对准，因此必须进行姿态补偿。以全循环法为例，时序如图5所示。

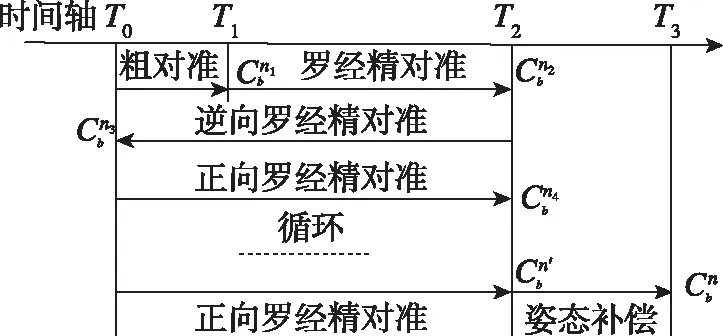
图5 基于姿态补偿的初始对准时序图Fig.5 Sequence diagram of the initial alignment method based on attitude compensation

本文设计了一次姿态补偿和接续姿态更新两种补偿方法，具体如下：

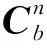
(14)

(15)

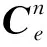
(16)

(17)

(18)

接续姿态更新法：初始对准前，事先约定循环计算使用数据长度的时间T2。在T2时刻开始循环解算，同时存储T2时刻之后的采样数据；在获得T2时刻精确姿态矩阵后，以其为初值，利用T2时刻之后存储的惯组数据进行姿态更新解算；一直更新到最新采样数据时刻T3，此时初始对准结束，从而获得了最新的姿态矩阵。

5.2 摇摆状态下仿真试验验证

为了验证两种补偿方法的正确性，在摇摆状态下进行仿真试验，摇摆模型为三轴正弦摇摆。约定本文中对准姿态角和对准误差均按照俯仰角、横滚角和航向角的顺序书写，惯组数据均从轨迹发生器中获得。这里采用一次正向捷联罗经精对准代替循环法对准，初始姿态角为：0°，0°，30°；粗对准误差为：1°，1°，5°；T2取值800s，假设导航计算机计算耗时为13s，T3取值813s。813s时刻姿态角真值从轨迹发生器中直接获得，按照俯仰角、横滚角、航向角的顺序分别为1.9021°、2.8532°和26.7693°。仿真试验结果见表1。

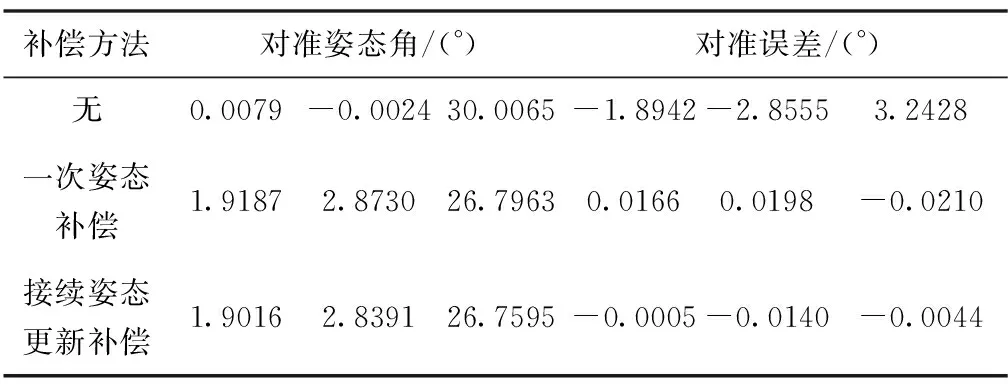
表1 姿态补偿对准仿真试验结果表

分析表1，如果对800s对准结果进行13s姿态补偿，最终对准精度将大大提高，否则误差很大。

5.3 行进状态下仿真试验验证

通常舰船和车辆等载体在初始对准时，速度不高，运动比较平稳，但也会出现加速、减速或转弯等现象，导致速度和航向角发生变化，因此也需要进行姿态补偿。这里以全循环法为列，时序如图6所示。

图6 行进状态下基于姿态补偿的全循环法初始对准时序图Fig.6 Sequence diagram of full cycle initial alignment based on attitude compensation in moving state

假设载体初始时刻姿态角为0°、0°、30°，从T1时刻开始以1m/s的视加速度向北作匀加速运动10s，之后先进行右转弯10s，接续进行左转弯10s，转弯时转动角速率恒定为0.0175rad/s(大约转动1(°)/s)，之后匀速行驶280s，再进行右转弯10s，后保持匀速运动。在前10s完成粗对准，T1取10s，T2取300s，假设导航计算机解算耗时30s，即T3取330s。采用三种方法进行仿真试验：常规捷联罗经对准、全循环捷联罗经对准和半循环法捷联罗经对准。全循环捷联罗经对准共进行3次正向罗经精对准，2次逆向罗经精对准，采用真实300s数据等效1500s数据；半循环法捷联罗经对准共进行3次正向罗经精对准，2次逆向姿态解算，采用真实300s数据等效1500s数据；作为对比，常规捷联罗经对准采用330s真实数据完成对准。三种方法均采用水平调平+方位估算粗对准方法，过程一样，仿真试验结果中只对比精对准过程，具体如图7～图9所示。

分析图7常规法仿真试验结果，对准误差为-0.0044°、0.0018°和0.1845°。

分析图8全循环法仿真试验结果，300s时刻对准姿态角为0.0057°、0.0002°和29.9763°，对准误差为-0.0042°、-0.0021°和0.0244°。从轨迹发生器获得330s时刻姿态角为0.0010°、0.0008°和20.0009°。补偿后获得最终姿态角为0.0057°、0.0009°和19.9761°，最终误差为0.0047°、0.0001°和-0.0248°，精度符合要求。

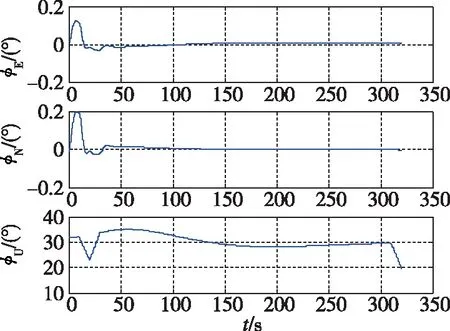
图7(a) 行进状态常规法对准姿态角图Fig.7(a) Alignment attitude angle by conventional method in moving state

图7(b) 行进状态常规法对准误差图Fig.7(b) Alignment error by conventional method in moving state

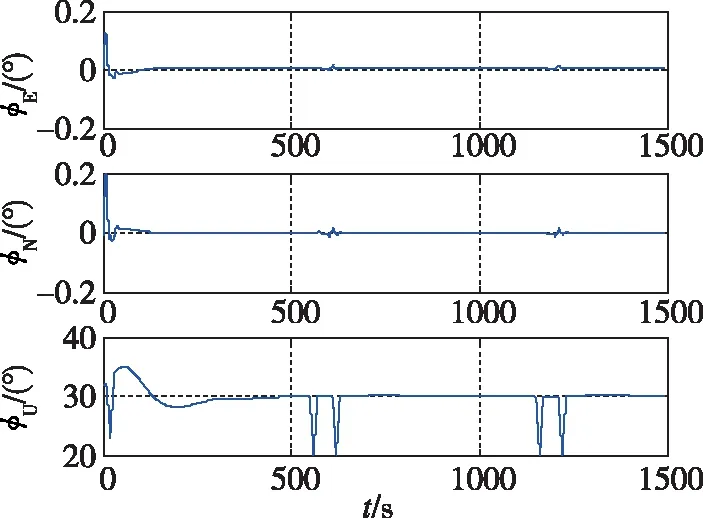
图8(a) 行进状态全循环法对准姿态角图Fig.8(a) Alignment attitude angle by full cycle method in moving state

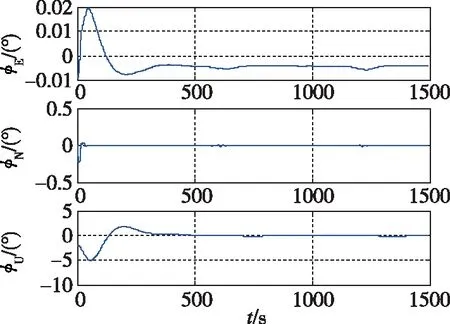
图8(b) 行进状态全循环法对准误差图Fig.8(b) Alignment error by full cycle method in moving state

图9(a) 行进状态半循环法对准姿态角图Fig.9(a) Alignment attitude angle by half cycle method in moving state

图9(b) 行进状态半循环法对准误差图Fig.9(b) Alignment error by half cycle method in moving state

分析图9半循环法仿真试验结果，300s时刻对准姿态角为0.0056°、0.0002°和30.0383°，对准误差为-0.0041°、-0.0021°和0.0357°。从轨迹发生器获得330s时刻姿态角为0.0010°、0.0008°和20.0009°。补偿后姿态角为0.0054°、0.0009°和20.0382°，计算出最终误差为0.0044°、0.0001°和-0.0373°，精度符合要求。

因此，经过姿态补偿后，基于正逆向导航解算的捷联罗经全循环法和半循环法,在动基座条件下均能完成初始对准，在同等时间和参数条件下，对比常规捷联罗经对准方法，其对准精度高，且缩短了对准时间。

6 基于正逆向导航解算的变参数捷联罗经初始对准研究

当粗对准误差较大时，精对准必须加快收敛速度，尽快将误差降下来；当误差较小时，如果继续保持振荡频率，那么就不利于收敛区域稳定，有可能一直振荡，或者需要更长的初始对准时间。因此，本文提出了基于正逆向导航解算的二级变参数捷联罗经对准方法。

6.1 正逆向二级参数配置

现以全循环法为例进行分析，具体参数配置示意图如图10所示。

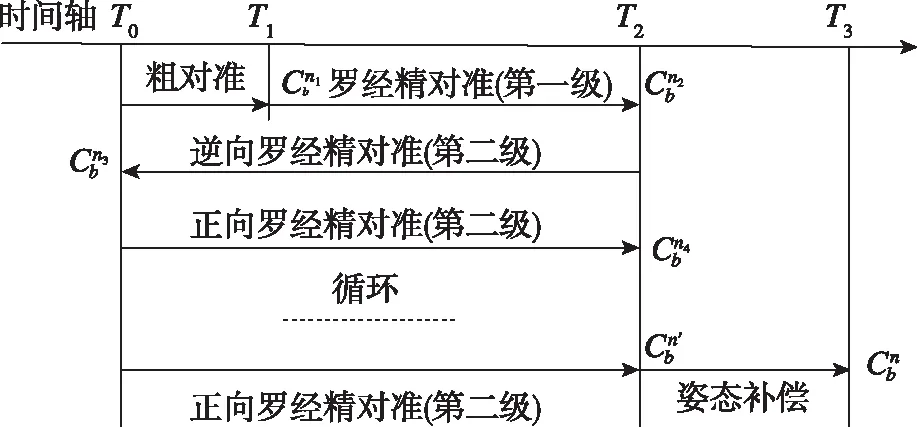
图10 正逆向二级变参数配置示意图Fig.10 Schematic diagram of forward and reverse two-stage parameter configuration

1)第一级参数：第一级参数配置在第1次正向罗经精对准中，强调前期对准过程的收敛速度，罗经方位调节参数Tz取小值，提高振荡频率，加快收敛。经过大量仿真试验可知，当ξ取0.707时，在第1个Tz处，航向误差一般降低至原误差的4%～6%之内，甚至更低，满足小角度要求。如果粗对准结束后误差已经很小，那么在Tz内会进一步减小振荡，保证了第1次正向罗经初始对准结果能为后续罗经精对准提供更高品质的初值。

2)第二级参数：第二级参数配置在后续正逆向循环中，强调后期对准结果的稳定性，罗经方位调节参数Tz取大值，提高了最终精度的稳定性。

6.2 仿真试验及验证

在摇摆和行进两种状态下进行仿真试验，以给定误差作为粗对准结果，直接参与罗经精对准。给定粗对准误差为1°、1°、10°，以全循环法为例进行仿真试验，固定参数和变参数两种方法均进行3次正向罗经精对准和2次逆向罗经精对准。摇摆状态仿真实验，T2取260s，固定调节参数：Txy=20，Tz=100;变调节参数：第一级调节参数Txy=20，Tz=100，第二级调节参数Txy=20，Tz=200。其他条件同5.2节，仿真试验结果分别如图11(a)和图11(b)所示。行进状态仿真试验，载体运动状态同5.3节，T2取200s，固定调节参数：Txy=20，Tz=100;变调节参数：第一级调节参数取Txy=20，Tz=100，第二级调节参数Txy=20，Tz=200。仿真试验结果分别如图12(a)和图12(b)所示。

图11(a) 摇摆状态固定参数对准误差图Fig.11(a) Alignment error by fixed parameters in swing state

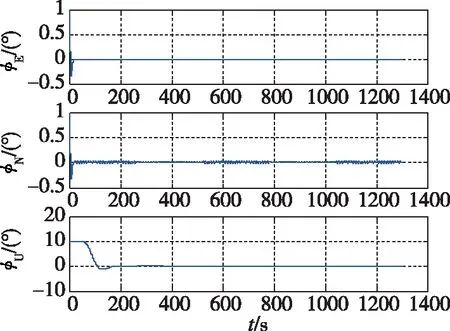
图11(b) 摇摆状态变参数对准误差图Fig.11(b) Alignment error by variable parameters in swing state

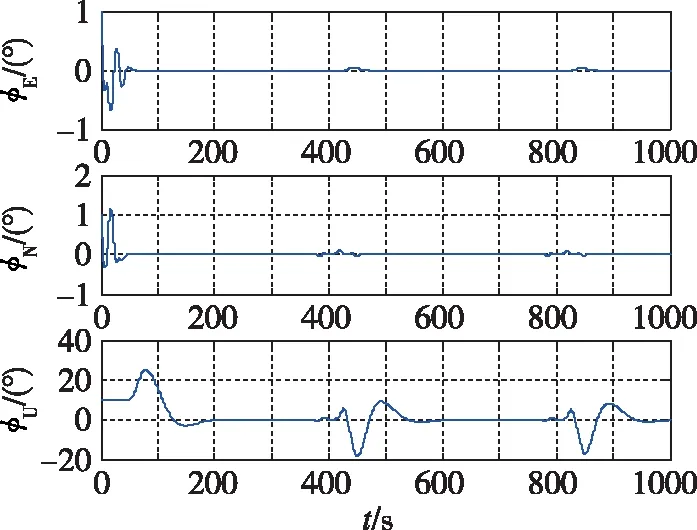
图12(a) 行进状态固定参数对准误差图Fig.12(a) Alignment error by fixed parameters in moving state

图12(b) 行进状态变参数法对准误差图Fig.12(b) Alignment error by variable parameters in moving state

分析图11(a)，对准误差为-0.0082°、-0.0018°和0.1349°，没有达到对准要求，再增大正逆次数后，继续小幅振荡，几乎没有提高；分析图11(b)，对准误差为-0.0078°、-0.0018°和0.0038°，达到了对准要求。

分析图12(a)，对准误差为-0.0043°、-0.0029°和-0.1730°，没有达到对准要求，再增大正逆次数后，继续小幅振荡，几乎没有提高；分析图12(b)，初始对准误差为-0.0043°、-0.0029°和-0.0006°，达到了对准要求。

因此，采用变参数法对准经过第一级对准后，误差迅速收敛到要求范围内，在第二级对准中超调量逐渐减小，误差很快趋于稳定。

7 结论

本文重点研究了逆向导航解算在捷联罗经初始对准中的应用问题，在全循环正逆向对准和半循环正逆向对准方法的基础上，针对提升基于正逆向导航解算的捷联动基座对准实时性的问题，提出了基于姿态补偿的对准方法。该方法能够减小在循环解算过程中因外界环境变化导致姿态角变化而产生的新误差，从而提高了对准精度，实现了基于正逆向导航解算的捷联罗经动基座初始对准。针对动基座中粗对准误差过大导致精对准时间延长的问题，提出了正逆向二级变参数配置方法，加快了对准过程中误差收敛速度，缩短了对准时间。最后进行了仿真试验验证，证明了在动基座条件下全循环法和半循环法均能在同等参数和时间条件下提高对准精度,对比常规捷联罗经对准方法，缩短了对准时间。