二维弹道修正引信转角控制翼面角度测量方法
2021-09-09徐渊源范清田张小虎
徐渊源,王 森,范清田,张小虎
(1.机电动态控制重点实验室,陕西 西安 710065;2.西北工业集团有限公司,陕西 西安 710043)
0 引言
二维弹道修正引信能够实现无控弹药智能化、灵巧化,减少弹药的消耗和后勤保障的压力,是实现低成本精确打击的有效手段[1]。固定翼二维弹道修正引信通过控制外弹道中翼面的转动角度从而改变弹丸的飞行姿态,进而通过变化的气动力为弹丸提供持续的修正力,最终实现弹道修正功能,故二维弹道修正引信翼面转角的准确控制对实现弹道修正具有重要意义。
二维弹道修正引信通常采用鸭舵修正方案[2-3],在炮射环境下,如155 mm榴弹平台,弹丸出炮口转速约为300 r/s,固定翼相对弹丸反转,转速更高,从而导致转角控制时翼面角度测量难度大,不易观察,并且进行炮射实验需要消耗弹药且须在满足相应射程的靶场进行,成本较高。
目前,国内多家高校及科研院所正在开展相关的研究工作,但对翼面角度使用地面设备测量的分析未见报道。地磁场具有良好的矢量特性和稳定性,磁传感器具有价格便宜、无积累误差、抗高过载、可以全天候工作等众多优势[4-5],因此,针对在炮射环境中转角控制翼面角度测量难度大、成本高的问题,本文提出了一种基于地磁检测的固定翼二维弹道修正引信转角控制翼面角度测量方法。
1 相关坐标系及固定翼二维弹道修正引信工作原理
1.1 相关坐标系
计算过程中涉及到地磁矢量在多个坐标系之间的转换,于是根据外弹道学的相关知识,对这些坐标系进行定义[6],以便推导相关结论。
1) 地理坐标系OXeYeZe(E)
如图1所示,其原点在炮口断面中心,OXe轴沿水平线指向地理东,OYe轴沿水平线指向地理北,OZe轴按右手法则确定为垂直向上。

图1 地磁矢量在地理坐标系的分量Fig.1 Geomagnetic vector component in geographic coordinate system
地磁矢量为H,其强度为H,磁偏角为D和磁倾角为I,磁偏角D是OYe轴与地磁矢量在OXeYe面上的投影的夹角,方向规定北偏东为正;磁倾角I是地磁矢量与水平面的倾角,规定向下为正,则地磁矢量在地理坐标系可表示为:
(1)
如图2所示,其原点在炮口断面中心,OXn轴沿水平线指向射击方向,OYn轴铅直向上,OXnYn铅直面称为射击面,OZn轴按右手法则确定为垂直于射击面指向右方。射向ψ为从OYe轴到OXn轴转过的角度,北偏东为正。

图2 地理坐标系与发射坐标系Fig.2 Geographic coordinate system and launch coordinate system
则地磁矢量在发射坐标系可表示为:

(2)
3) 准弹体坐标系OXaYaZa(A)
如图3所示,其原点在弹体的质心,OXa轴沿弹轴指向弹体头部方向,OYa轴垂直OXa轴向上,OXaYa铅直面称为射击面,OZa轴按右手法则确定为垂直于OXaYa平面指向右方。φ为航偏角,θ为俯仰角。
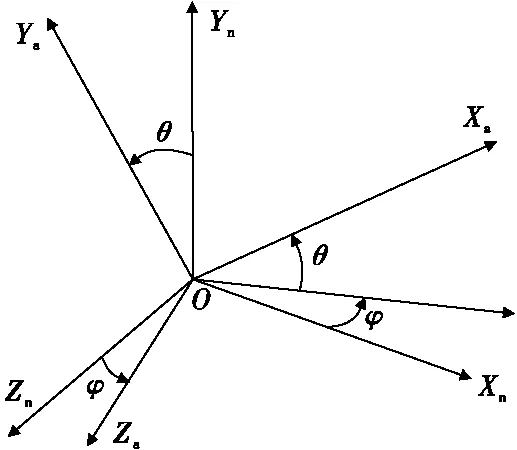
图3 发射坐标系与准弹体坐标系Fig.3 Launch coordinate system and quasi-projectile coordinate system
根据坐标系之间的转换关系,则有地磁矢量在准弹体坐标系的表达式为:

(3)
1.2 固定翼二维弹道修正引信工作原理
二维弹道修正引信主要由引信主体和修正执行机构两部分构成,如图4所示。引信主体通过螺纹与弹丸连接,修正执行机构部分包括电机和固定翼,固定翼与引信主体通过轴承连接,可以相对转动。三轴磁传感器安装于引信主体的头部结构内,安装方式为:磁传感器x轴沿弹轴方向安装,磁传感器的y轴和z轴垂直于弹轴方向安装,磁传感器的输出和电机的控制信号有关。固定翼修正执行机构包含两对翼面:一对翼面为导转翼面,为修正执行机构提供导转力矩;另外一对为升力翼面,为弹丸提供修正力和力矩[7]。

图4 二维弹道修正引信示意图Fig.4 Schematic diagram of two-dimensional trajectory correction fuze
如图5所示,翼面1和翼面3为升力翼面,当升力翼面位于水平位置时,它们和过质心的铅直面是对称的,外弹道环境所受气动力为F1、F3所指向方向,对弹丸提供升力;翼面2和翼面4为导转翼面,当升力翼面位于水平位置时,它们和过质心的水平面不对称,外弹道环境所受气动力分别为F2、F4所指向方向,为整个固定翼面提供顺时针旋转(从头部向尾部方向观察)的导转力矩。固定翼二维弹道修正引信在进行弹道修正时,通过控制外弹道中翼面转动的角度,使翼面固定在某一确定方向,从而改变弹丸的飞行姿态,进而通过弹丸所受变化的气动力为其提供持续的修正力,最终实现系统的修正功能。

图5 固定翼结构原理图Fig.5 Schematic diagram of fixed wing structure
2 转角控制翼面角度测量数学模型
2.1 翼面转角分析
外弹道刚出炮口时,弹丸相对地面高速右旋,修正翼面相对地面左旋。当引信开始进行弹道修正(起控)时,修正翼面受电机提供的电磁力矩相对大地静止,只需要将翼面停至预期的位置便可使弹丸所受气动力发生变化,实现系统的二维弹道修正功能。为了方便计算翼面转动角度,规定一对升力翼面水平且所受气动力向上时(即图5翼面所处位置)翼面转角为0°,转角沿气动力转动方向(顺时针方向)为正。
他拿出一个信封,递到李萍手里,“我家那口子,没挺过三年就去了。大家当时凑给我的钱,我都一一还了,这是你的那五百。”
若转角控制相对准确,当装定控制后翼面转角的目标角为0°时,修正引信在空中起控后的翼面的姿态应和图5一致,即导转翼面2竖直向上。由于准弹体坐标系OXa轴和弹轴方向一致,OYa轴竖直向上,这时准弹体坐标系OYa轴和导转翼面2中心线的方向一致。因此当翼面转角的目标角为0°时,外弹道中地磁矢量与准弹体坐标系OYa轴的夹角等于其与导转翼面2中心线的夹角。
2.2 翼面转角计算及测量方法
如图6所示(从修正引信头部向尾部观察),地磁矢量在准弹体坐标系弹轴径向平面的分量为M,其强度为M,与准弹体坐标系OYa轴的夹角为α。则地磁分量M在OYa轴上的投影分量为:My=Mcosα;在OZa轴上的投影分量为:Mz=Msinα,则:
α=arctan(Mz/My)
(4)
由坐标转换关系,联合式(1)—式(3)可求出地磁矢量在准弹体坐标系的数值为:
Ha=L(θ,φ)L(ψ)He
(5)

图6 地磁矢量在准弹体系径向平面分量Fig.6 The radial plane component of geomagnetic vector in quasi-projectile coordinate system
由于My和Mz分别是地磁矢量在准弹体坐标系弹轴径向平面OYa轴和OZa轴上的分量,则My和Mz分别是Ha(1×3矩阵)的第二行、第三行的数值,即:
(6)
代入式(4)最终可求得α。分析可知夹角α和磁偏角D、磁倾角I、射向ψ、航偏角φ和俯仰角θ有关,与地磁矢量强度H无关(分子分母约除)。
在使用地面转台模拟炮射实验进行转角控制翼面角度测量时,用指南针或地磁检测仪测量地磁分量M在风洞双旋转台上的方向,并在转台上做好标记M。只需要给引信飞行控制模块装定炮射位置的磁偏角、磁倾角、射向及目标角,存储炮射试验的航偏角和俯仰角数据,便可计算出夹角α。从修正引信头部向尾部观察:为了方便观测,第一次装定目标角为0°,进行双旋试验起控时,图5中翼面2停止时中心线的位置应为标记位置M沿顺时针方向转动α;当装定任意的目标角ε(0°≤ε<360°),进行双旋试验起控时,翼面2停止时中心线的位置应为标记位置M沿顺时针方向转动β,且β=α+ε,由此便实现了固定翼二维弹道修正引信的转角控制在炮射环境翼面角度的测量。
3 验证
3.1 仿真验证
仿真时,由于计算结果与地磁矢量强度H的大小无关,故取H=1。装定某靶场的炮位参数磁偏角:D=-1.8°,磁倾角:I=56.4°,射向:ψ=-42°。飞行控制模块读取已经存储的炮射实验外弹道航偏角和俯仰角数据或者6D模型仿真的外弹道航偏角和俯仰角数据,目标角ε分别装定为0°、90°、180°、270°。
外弹道范围内地磁矢量在准弹体坐标轴OYa、OZa上的分量如图7(a)、(b)所示,它们的值与目标角无关。目标角ε分别装定为0°、90°、180°、270°时,仿真得到任意时刻起控(实际通常在弹道中后段起控)后,地磁矢量在准弹体坐标系弹轴径向平面分量M与导转翼面2中心线的夹角β图形如图8所示。

图7 地磁矢量在准弹体坐标轴上的分量Fig.7 The component of geomagnetic vector on coordinate axis of quasi-projectile coordinate system

图8 不同目标角下起控后β在外弹道变化Fig.8 Changes of β in exterior ballistics after control at different target angles
夹角β在不同目标角时变化趋势相同,在同一时刻大小相互相差90°。外弹道大约64 s,β在前22 s基本不变,22 s后随着控制时间的延续逐渐减小。例如,炮射后40 s开始起控,则在四种目标角起控时,β分别151°、241°、331°、61°,随着控制时间的延续β缓慢减小,从起控点到弹道末端β大约减小14°。
3.2 双旋转台验证
在双旋转台上进行转角控制实验时,先测出双旋转台上地磁分量M的方向,并做标记M(西安的磁偏角为2°29′)。飞行控制模块使用的所有射击参数与仿真相同,包括磁偏角D、磁倾角I、射向ψ、航偏角φ、俯仰角θ及目标角ε。当修正引信上电后,系统工作至起控时间(40 s)时,如图9所示,修正翼面2在不同目标角停止时中心线的位置分别为M沿顺时针方向转动154°、244°、334°、64°,随着控制时间的增加这个夹角缓慢减小,从起控点到弹道末端大约减小14°。
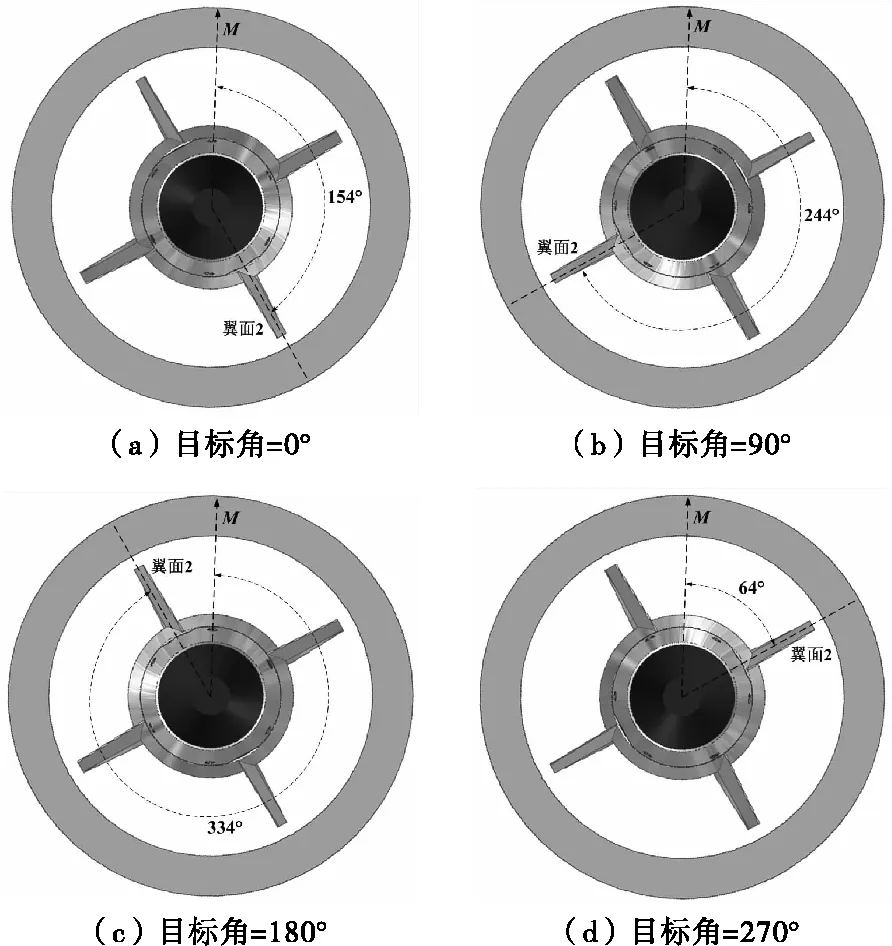
图9 不同目标角起控时翼面停止的位置Fig.9 The position where the wing surface stops when starting control at different target angles
实验中修正引信起控时翼面停止的位置分别与理论预期的角度相差3°,这是由于修正引信系统本身存在滚转角测量误差以及相对转角测量误差等,导致的转角控制结果与理论预期的角度有少量偏差,具体转角控制的角度误差与每发修正引信的自身系统测量误差有关。
4 结论
本文提出了固定翼二维弹道修正引信转角控制翼面角度地面测量方法。该方法利用坐标系转换关系计算出地磁矢量在准弹体坐标系弹轴径向平面分量与准弹体坐标轴之间的夹角,结合目标角的分析,计算出外弹道起控后地磁分量和翼面的夹角及其变化规律;接下来通过测量双旋转台径向平面上地磁分量的方向,飞行控制模块装定炮位相关射击参数,存储并读取炮射环境航偏角和俯仰角数据,最终在双旋转台实现二维弹道修正引信转角控制翼面角度的测量。仿真和实验结果表明,该方法能够方便、准确地实现固定翼二维弹道修正引信的转角控制在炮射环境翼面角度的测量,为二维弹道修正引信系统集成提供了必要的基础。分析表明,转角控制的角度与理论预期角度有一定误差,可以通过进一步研究系统的滚转角测量误差及相对转角测量误差,对系统的转角控制误差进行补偿。
