基于隐马尔科夫模型的动向目标运动趋势预测∗

娄洋歌 邹锦涛 周学平

（中国电子科技集团公司第二十八研究所 南京 210007）

1 引言

在现代防空作战中，随着探测侦察手段的不断丰富，侦获的非格式化动向情报越来越多，将准实时动向情报与实时航迹目标进行关联识别的需求尤为迫切。动向情报关联识别的前提是能够对侦收的动向情报进行运动趋势预测，建立准实时动向情报与实时航迹的关联关系，为目标识别的推理提供依据。

一般来说，传统的预测方法可以划分为定性和定量两类［1］。定性法主要是参考历史资料，利用个人经验、专业知识和综合研判能力，对事物将来的发展情况进行分析预测，该分析法缺点是主观性较强。定量法主要是融入基于数学算法的预测理论，通过数学方法对获取的数据进行统计、分析，以预测事物的发展趋势［2］。

目前，基于数学模型的预测方法主要有线性回归法、非线性回归法、Logistic函数拟合法、指数曲线拟合法、灰色系统预测法等［3］。后来，许多科研院所学者在已有方法的基础上，通过融入新的方法提出了新的数学预测模型。陈玉金、刘永健等人在神经网络的基础上提出了回归分析组合模型［4］；于振明等人在组合预测模型方法的基础上融入情景规划分析的方法［5］；芮海田等人提出在指数平滑算法的基础上通过利用马尔科夫模型预测客运量的方法［6］。

然而，以上研究基本上有大致相同的局限性，且数学模型复杂导致模型求解困难，在实际工程运用中要达到较快的运算速度和较高的计算精度，仍存在较大的难度。此外，现有文献中很少提及将预测方法用于动向目标运动趋势预测。

本文提出了利用隐马尔科夫模型（Hidden Mar⁃kov Model，HMM）对动向目标运动趋势进行预测的算法处理模型。首先，对实际获取的动向情报，提取动向要素。然后，利用基于决策树的方法对目标的动向要素进行关联聚类处理。最后，建立隐马尔科夫模型对动向目标的运动趋势进行目标状态预测。

图1 动向目标运动趋势预测流程

2 动向情报预处理

侦收的动向情报是非格式化的文本形式，预处理的基本任务就是从非格式化的动向文本中提取格式化的动向要素，通过预处理构建基于动向要素的特征向量，利用基于语义的决策树实现对动向要素的关联聚类处理，最终形成机器可认知的格式化结构，为动向目标的运动趋势预测提供支持［7～8］。

2.1 动向要素提取

假设给定的一个非格式化动向情报内容如下所示。

2014年08月29日05时59分，位我当面岛礁东南30°方共侦获美舰1艘，坐标310406N1260654E，研判为美驱逐舰。

可将上述动向情报内容表征为以＜发生时间、发生地点、目标行为、关联平台、关联机构＞等表示的格式化动向情报。动向要素主要包括结构化的时空信息和主体目标信息，采用分词系统对获取的原始文字情报进行分词处理，然后进行目标动向实体识别，提取动向情报中的时空信息和目标信息。在计算目标实体关联前，需要对各类获取的数据分别进行时空化的数据对准处理以统一数据格式，如图2所示。通常以模板方式来体现实体要素的表示方式，比如通过时间模板表示。模板为：数字+时|分|秒|点，例如，下午14hh：30mm：25ss。

图2 时空化数据分类处理

2.2 动向要素关联提取

动向要素提取主要采用基于概念树的处理方法，从根结点到叶子结点的排列来分类动向样本实例。

本文主要采用构造数字型概念树［9］的方法，具体的方法可以描述为将动向要素数据放入二维数据表中，利用动向要素数据的关系视图R={C}i=1r以及k-means聚类算法（聚类个数k为关系视图中R的某一概念数层的节点总数），将动向要素的数据分别划分成对应的集合以便关联关系视图中的节点概念。

如图3所示，对于目标动向要素的所属文字，概念树的各个结点代表了文字中目标动向要素的所属分类。决策树的上层节点一般是概念数中最有助于分类目标动向实例的属性，所以概念数的根结点一般可以表示特征向量中最优的属性。

图3 动向要素关联聚类示意图

3 基于隐马尔科夫模型的动向目标运动趋势预测

隐马尔科夫模型［10～11］可以通过数学符号λ=(A，B，π)表示，其中A={aij}是状态转移矩阵，aij为t时刻从状态Si转移到状态Sj的数学概率；概率分布矩阵B={bik}；初始状态概率πi=P(q1=si)，它表示在初始时刻选择某个状态的概率。该模型的具体算法流程如图4所示。

图4 隐马尔科夫模型算法流程图

一个已知的HMM能够形成观测序列O={o1，o2，…，oT}，ot表示在t时状态为Sj的观察值。隐藏状态序列Q和可观察状态序列O的联合概率为

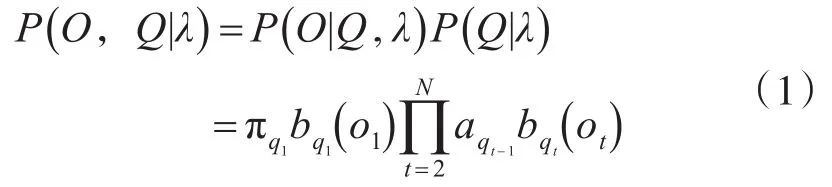
其中，P(O，Q|λ)为观察序列O的概率，P(Q|λ)为隐藏状态序列Q在该HMM下的概率。由于式（1）的计算量很大，本文通过利用后向算法减少式（1）计算量大的问题。隐马尔科夫模型λ，在时刻t且状态为qi时，从t+1到T的部分观测序列Ot+1，Ot+2，…，OT的概率为后向概率，公式为

本文采用隐马尔科夫模型作为对动向目标运动趋势进行预测的系统模型，利用语义决策树对动向要素进行聚类得到几个隐含状态，实现将动向目标运动趋势转化为动向目标的运动状态预测。用动向目标相对应的真实的空间位置表示观测对象，建立隐马尔科夫模型，由式（3）得到预测序列的概率。

本文实现维特比算法计算动向目标的最优状态序列：

输入：λ=(A，B，π)和观测序列S=xt1，xt2，…，xtN；输出：最优状态序列。

最后，根据动向目标的趋势概率分布，系统采用扇形波门的形式，构建关联区域，扇形关联区域表现形式如图5所示。

最终的概率公式为

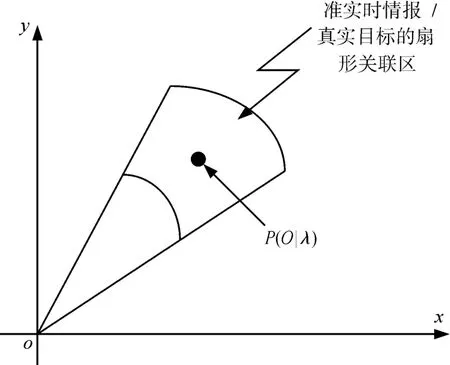
图5 扇形关联区

4 实验分析

本实验主要以侦获的空中动向目标为基础，利用基于隐马尔科夫模型对动向目标的运动趋势进行预测。然后采用均方根误差来计算衡量模型预测的位置精度。实验中，每隔1min预测一次，然后分别计算预测的经度和纬度与观测值的均方根误差的值。

均方根误差公式表示为

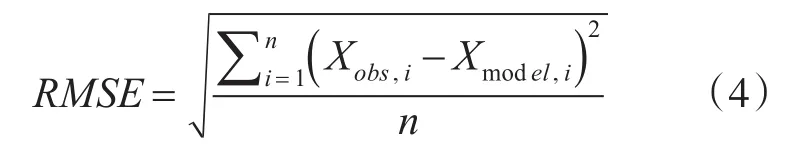
Xmodel，i是下一时刻位置的观测值，Xobs，i是预测值，n是预测次数，RMSE的值越小说明模型越好。

观测值与预测值之间距离的公式表示为

其中，(x1，y1)为观测值的坐标，(x2，y2)为预测值的坐标。

对动向目标运动趋势进行预测的预测值与观测值的比较曲线如图 6（a）所示，从图6（a）中可以看出，本文提出的基于模型预测的动向目标运动趋势的预测值在经过多次预测后较接近于观测值，能较好地反映真实目标的运动趋势。

该模型对应的预测精度的均方根误差曲线如图6（b）、（c）所示，从图6（b）、（c）中可以看出，在进行多次预测之后，经度和纬度的均方根误差逐渐收敛。

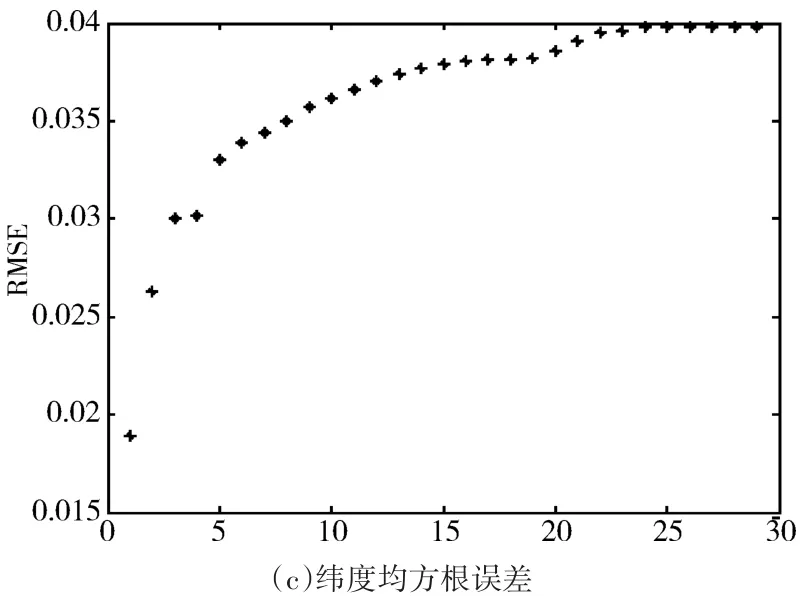
图6 预测值与观测值比较及对应的经纬度均方根误差

对动向目标的运动趋势进行预测后，需与实时目标进行位置关联［12～13］，本文采用的关联门限定义如下：

1）预测值与观测值的距离在0～5km为确定关联；

2）预测值与观测值的距离在5km～10km为模糊关联；

3）预测值与观测值的距离在大于10km为不关联。

基于上述定义的位置关联门限，统计实验中属于确定关联、模糊关联和不关联的具体点数，具体点数如表1所示，本文定义处于模糊关联的点可认为为关联点。

表1 动向目标与实时目标关联点数统计

由表1可知，确定关联和模糊关联的点数和为25，占总点数的86.2%。可见，动向目标的运动趋势预测结果能够为与实时目标的关联提供有效依据。

5 结语

在对提取的动向要素建立特征向量的基础上，本文提出了基于隐马尔科夫模型的动向目标运动趋势的预测方法。经过实验验证，该模型预测的动向目标的运动趋势与观测值接近，在进行多次状态预测之后，误差增长趋于平缓。此外，在本文提出的关联规则中，动向目标运动趋势的预测结果能够为动向目标与实时目标的关联提供依据。

由于空中目标机动时的航向、速度变化较大且较快，该模型不适应机动目标的运动趋势预测，在后续研究中，可以进一步开展机动目标的运动趋势预测研究。