基于Freeman 链码改进图像处理算法的指针式仪表识别

李贵良,李 博,陈德帛,罗新元,郭 祥,罗永盛

(云南电网有限责任公司,云南 昆明 650041)

0 引言

随着大数据时代的到来和“工业4.0”的提出与实施,各类数字仪表(如电流表、电压表)在日常生活、学习与工作中的使用数量急速增多。 在我国智能化道路发展速度加快的背景下,机器人已逐步替代了传统人工作业。 这也在一定程度上扩大了指针式仪表的应用范围[1-3]。 但指针式仪表存在不足之处,如电磁干扰、数据变化过快等[4]。 针对上述情况,有学者提出了基于Freeman 链码图像处理算法的指针式仪表识别技术。 研究表明:该技术整体效果优异,可惜尚未得到推广与普及[5-6]。 本文以上述研究为基础改进了该算法,并进行了试验验证。

1 基于Freeman 链码改进图像处理算法的图像描述

图形学理论认为:视频图像的轮廓中,每个点至少存在1 个方向与8 个链码方向之一相互对应;每个像素点与其相邻像素点的8 个方向便可视作8 个链码值。 如按一定顺序对其进行标记,便可形成最终集合,即Freeman 链码[7]。 假设闭合曲线值起始位置后的第i个像素的链码值为ai,ai∈{0,1,...,7},L、L1分别代表某像素点、要跟踪的像素,此时满足ai=1。 若将起始点记作L0、终点记作L7,按标记顺序将标记点图像并应用Freeman 链码扫描,便可形成矩阵邻域的一次链码整理。 Freeman 链码的方向取值如图1 所示。

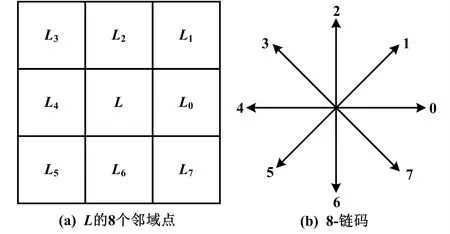
图1 Freeman 链码的方向取值Fig.1 Direction value of Freeman chain code

由图1 可知,若将矩阵邻域看作不同的点并将其边缘按一定顺序连接起来,便可形成Freeman 链码边缘表述。 根据图像处理理论进行图像信息描述。 其中:将特征信息部分像素视作1、背景像素视作0,按从下至上、从左往右的方式寻找像素值为1 的点。 将L0(a)下一个搜索点的灰度值看作1,并将其命名为起始点左上方的像素点。 按顺时针方向每次旋转45°,依次重复上述步骤直至找到起始点为止。 Freeman 链码的边缘表述与邻域如图2 所示。

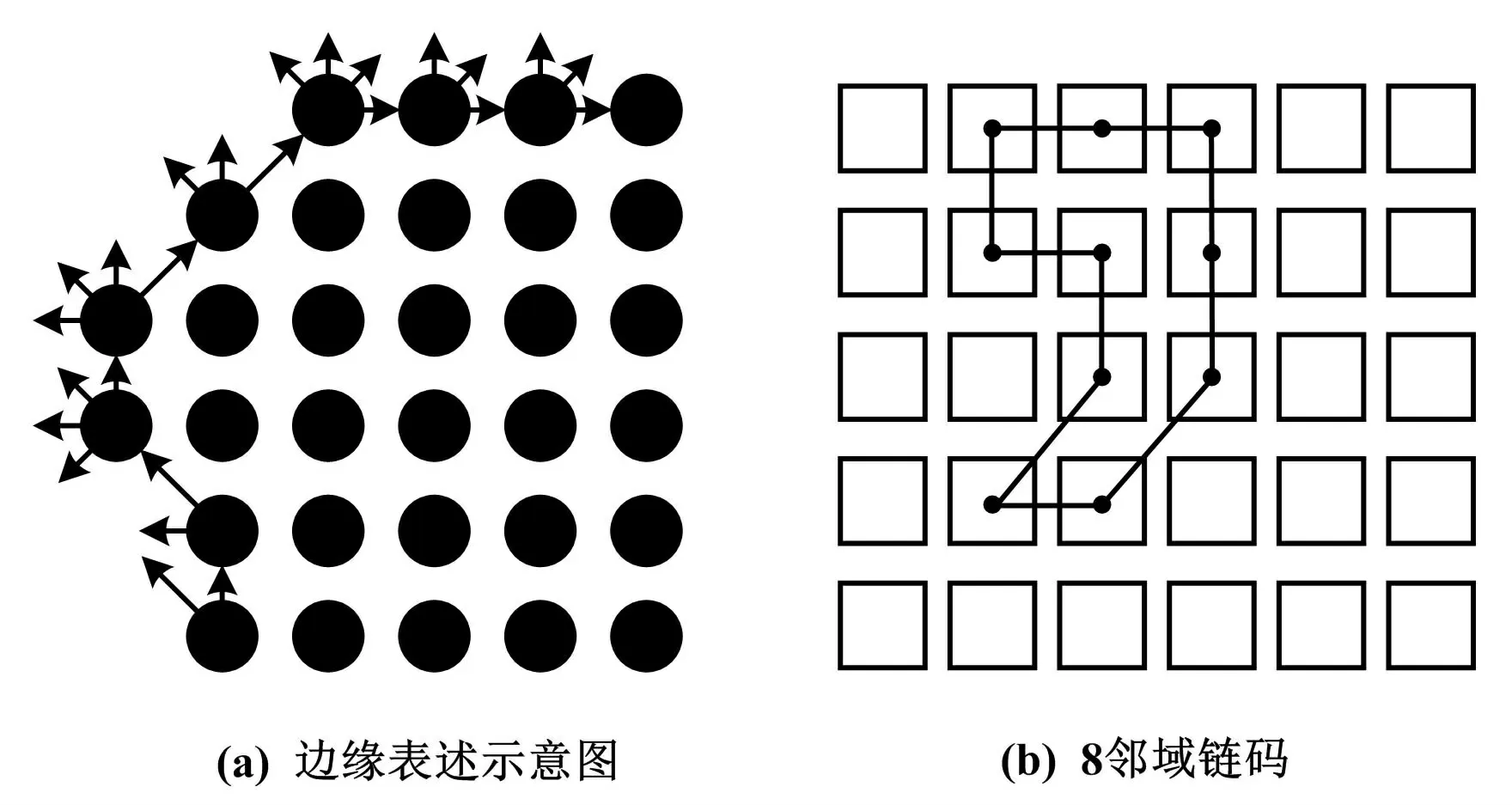
图2 Freeman 链码的边缘表述与邻域Fig.2 Edge representation and neighborhood of Freeman chain codes

由图2 可知,影响图像处理中Freeman 链码分割效果好坏的因素主要是种子点、生长原则和终止条件。基于Freeman 链码改进图像处理算法的区域生长过程如图3 所示。 由图3 可知,不同生长原则下的图像生长区域与结果均不同,且二者均受灰度值、纹理、颜色、梯度等因素的影响。

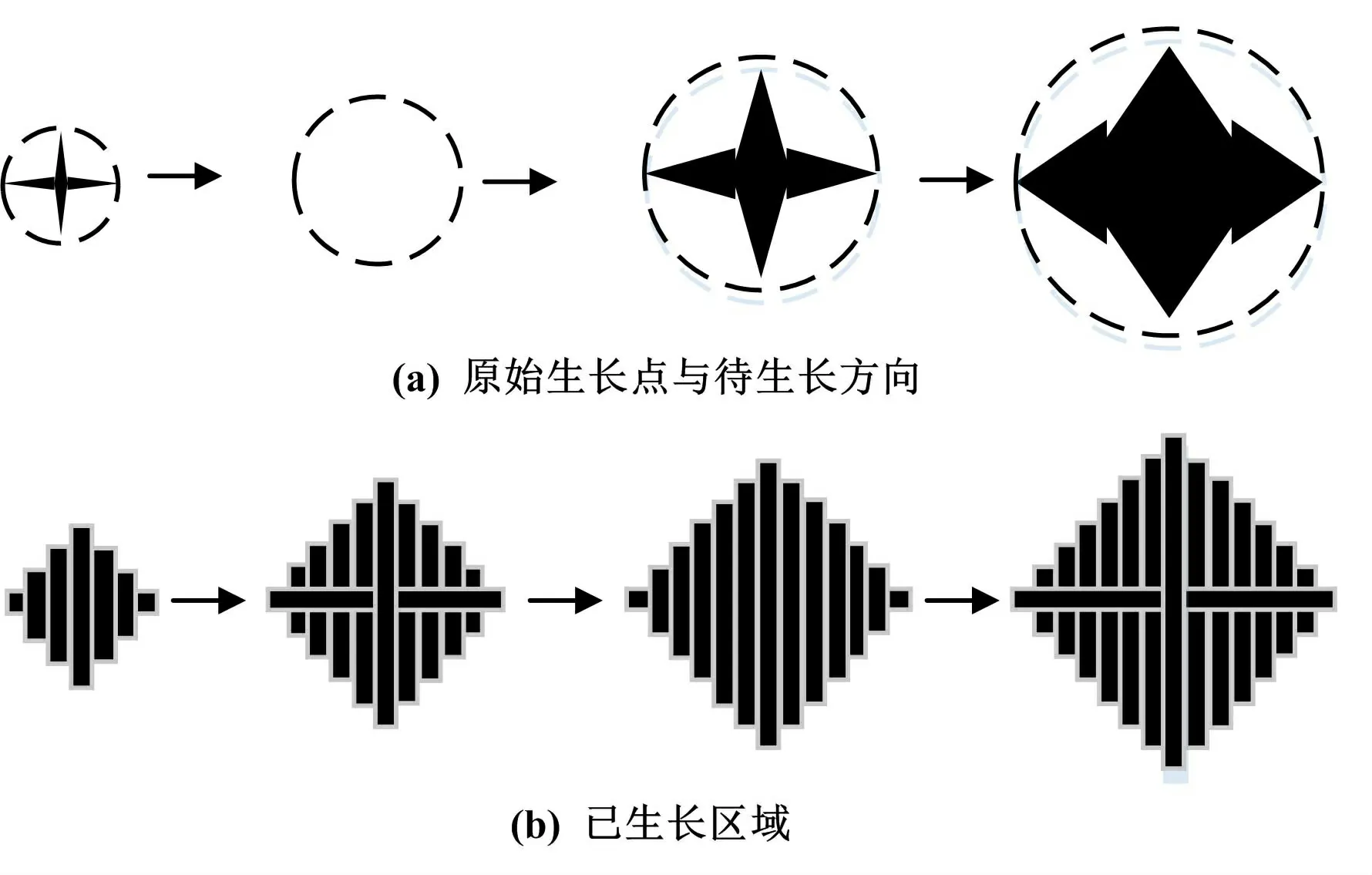
图3 基于Freeman 链码改进图像处理算法的区域生长过程示意图Fig.3 Regional production process of improved image processing algorithm based on Freeman chain code

在图3 的基础上,假设Freeman 链码改进图像处理算法中的图像I的生长区域为R,Np为像素p的邻域,其中两个像素p、q(p∈R,q∈Np)之间的距离为dpq,应用欧几里法得出距离为ρ。 当ρ=1 时,Freeman链码改进图像处理算法中的图像的矩阵呈四邻域状态。 式(1)、式(2)表示不同限制条件下的两类像素集。

2 基于Freeman 链码图像处理算法的改进

2.1 基于Freeman 链码图像处理算法优化

噪声是影响指针式仪表性能的主要因素,也是其试验预处理中的关键环节[8]。 指针式仪表识别技术的应用通常会涉及边缘检测,主要包括滤波检测、增强边缘、效能检测3 个步骤。 为改进基于Freeman 链码图像处理算法,本文将引入约翰·肯尼(John Canny)边缘算法,对指针式仪表性能中存在的不足之处进行优化处理[9-10]。 设标准差为E(满足1.4 的5×5 高斯函数内核),如式(3)所示。

依照Sobel 滤波器操作步骤,使用以下卷积矩阵,即可得式(4)。

由表1 可以看出,Canny 算子、Sobel 算子在基于Freeman 链码图像处理算法中各有优势,但方框滤波和均值滤波处理下的指针式仪表图片过于模糊,高斯滤波处理下的指针式仪表图片关键信息缺失。 此次研究最终决定使用Canny 算子、Sobel 算子作为本文的预处理方法。 霍夫线变换原理如式(5)所示。

表1 不同边缘检测算子在指针式仪表检测中的耗时对比表Tab.1 Time consumption comparison of different edge detection operators in pointer instrument detection s

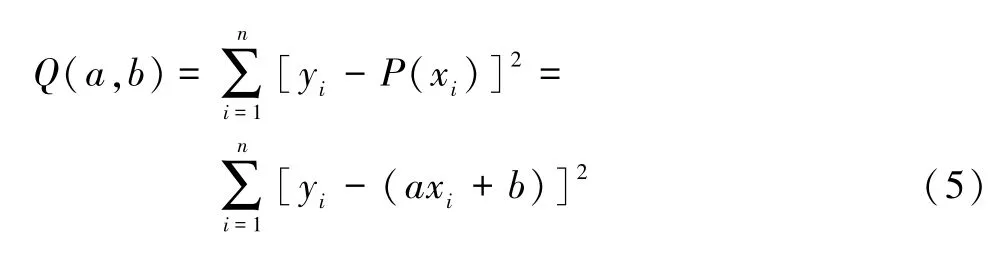
式中:i为指针式仪表中的任意正整数;(xi,yi)为提取的像素点;P(xi)=axi+b为数点所连成的直线,a、b分别为斜率、截距;Q(a,b)为函数驻点;n为像素点数。需注意的是,若Q(a,b)梯度为0 时,点(a,b)需满足以下两个条件,如式(6)所示。

对式(6)求解,得a、b的方程组,最终可得满足指针式仪表中的像素点直线方程:y=ax+b。 为判定直线(霍夫变换)是否与x轴垂直,设β为任意小的正数。在此条件下若绝大多数像素点的横坐标值均在(x-β)～(x+β)之间,则上述基于Freeman 链码图像处理算法的假设成立。 同时,将直接坐标系调换为yOx,并将y设为横坐标,可得直线方程:x=cy+d。 表盘直角坐标系如图4 所示。

图4 表盘直角坐标系Fig.4 Dial rectangular coordinate system

如图4 所示,设圆心点(x,y)和半径r构成的三维空间的圆的2 个直线的参数分别为r、θ,圆心为(xcenter,ycenter,r)。 刻度值计算如式(7)所示。

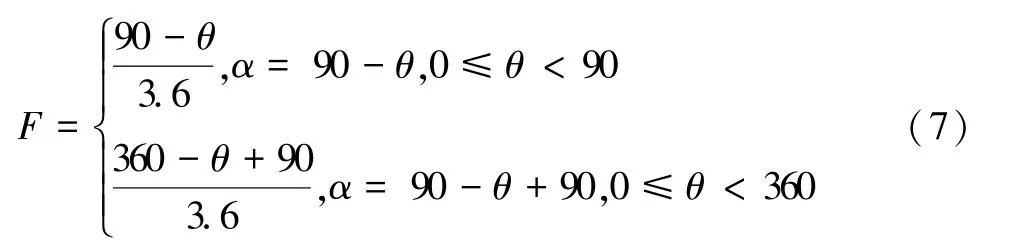
式中:θ、α分别为提取角度、零刻度与指针CP的夹角,每一度的刻度值(F)为1/3.6。

设经过Freeman 链码处理后的特征图像,得λ 取值计算式,如式(8)所示。

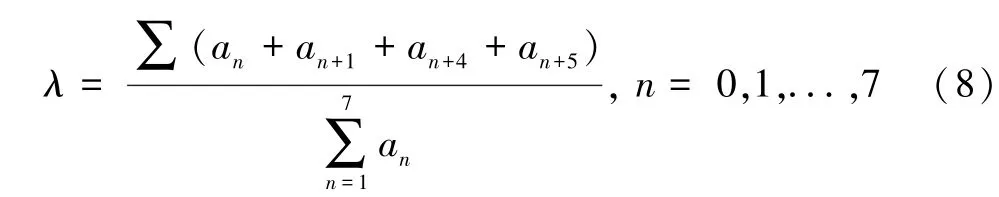
式中:λ为方向链码占比;an为8 个不同方向的链码,n=0,1...,7。

当特征方向链码占比大于所有链码75%(即T=0.75)时,在式(8)的基础上继续设指针式仪表的指针的2 个定点与底点所在的位置分别为ppeak、pbottom,即仪表指针的直线;而指针直线的倾斜角度定义为θ。 按式(9)所示的反三角函数即可求出θ。

式中:θ、θ0分别为待测指针偏转角度、指针量程最小值与指针指向表盘中间位置的偏转角度;K、K0分别为待测指针示数、待测指针示数;(x1,y1)、(x2,y2)分别为指针的2 个坐标;M为仪表指针旋转一周的理论测量值。

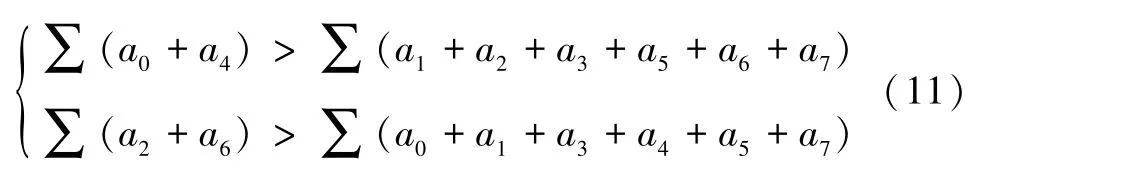
需注意的是,由于式(10)存在2 种不同方向,即水平与竖直方向,故还需满足式(11)。

综合经灰度化处理、滤波增强、边缘检测、Freeman链码处理后的各项数据可知,Canny 算子虽然图像处理时间相对较长,但能更直观地反映仪表的数值。 指针式仪表示数识别如图5 所示。

图5 指针式仪表示数识别图Fig.5 Indication recognition diagram of pointer instrument

接着对本文算法的识别准确性进行验证,得出不同算法下的仪表示数对比如表2 所示。 由表2 可知,将上文中的霍夫变换算法与本文中的基于Freeman 链码改进图像处理算法用于自指针式仪表的示数识别结果进行对比后,发现本文算法的耗时均高于霍夫变换算法。 本文算法最大相对误差为0.04%,而霍夫变换算法的最大相对误差为1.23%。 故相较而言,本文提出的基于Freeman 链码改进图像处理算法在指针式仪表的应用中的性能更好。

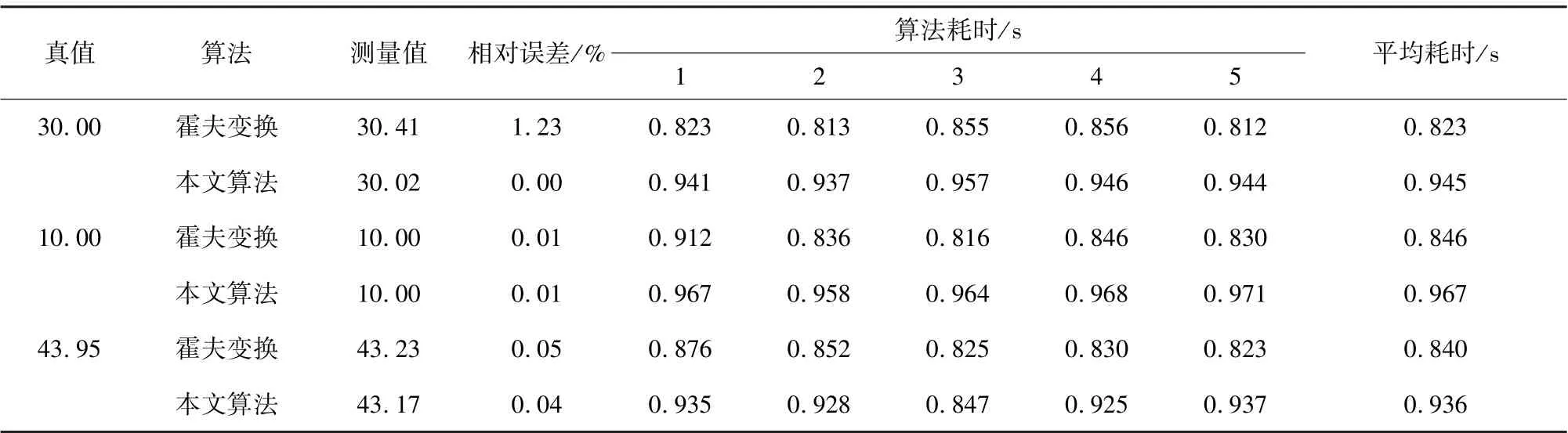
表2 不同算法下的仪表示数对比Tab.2 Comparison of instrument indication under different algorithms

2.2 基于Freeman 链码图像处理算法的二次校正

透视投影、平行投影是目前图像处理领域中应用较多的2 种图像处理投影方法,可实现从三维立体信息到二维平面信息的转换。 透视投影的标准几何模型与透视变换模型如图6 所示。 相较而言,如图6(a)所示的透视投影作为摄像机捕获图像信息的标准几何模型,应用价值较平行投影更高。 但由于不同角度拍得的图像不同,畸变也不一样。

当视点为E时,平面物体(P)必须穿过P1才能观察得到,这便是常规的透视图模型。 但若投影视角存在一定倾斜时,图像便会畸变。 而在透视变换后,图像所对应的点也会随之改变。 如图6(b)所示,即A1→A、B1→B、C1→C和D1→D。

为有效校正图像畸变,设变换图6 参数分别为a、b、c、d、e、f、g、h,并按由左往右进行适当校正,如式(12)所示。

图6 透视投影的标准几何模型与透视变换模型Fig.6 Standard geometric model and perspective transformation model of perspective projection

式中:(x,y)、(u,v)分别为变换前坐标、变换后坐标。

根据式(12)找到透视图与正视图的4 个对应点的投影图坐标(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4)和正视图坐标(u1,v1)、(u2,v2)、(u3,v3)、(u4,v4),并设变换参数为M,Z=AM、M=A-1Z,F=PM,如式(13)所示。

根据式(13)可求出基于Freeman 链码图像处理算法的透视变换矩阵。 通过对最左边至最右边的4个图分别进行校正,即选取一次校正后圆上的4 个匹配点,分别作圆在这4 个校正点方向的切线,使其在不同阶段均形成1 个新的矩阵,并分别对倾斜圆进行校正。 根据式(12)、式(13)进行计算,即可实现对图像的二次校正。 倾斜至二次校正的变化过程如图7 所示。

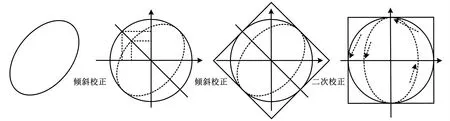
图7 倾斜至二次校正的变化过程Fig.7 Change process of tilt to secondary correction

3 试验结果验证与分析

3.1 基于本文算法的指针式仪表的斜率校正验证

在指针式仪表的图像识别过程中,水平、垂直和混合倾斜是影响指针式仪表自动识别的主要原因。 所获图像可能存在倾斜,这是其图像畸变的主要因素[11-12]。 在此进行斜率校正验证,不同刻度值下的指针识别结果如表3 所示。

表3 不同刻度值下的指针识别结果Tab.3 Pointer recognition results under different scale values

由表3 可知,相较于人眼宏观度数识别,本文所提出的基于Freeman 链码改进图像处理算法的指针式仪表识别技术的准确性、可靠性均更接近真实值。 倾斜校正效果如图8 所示。

图8 倾斜校正效果图Fig.8 Tilt correction effect

根据式(14)实现第一步校正。 效果如图8(c)所示。 接着采用霍夫变换和透视变换理论对一次倾斜校正图像进行第二次校正,实现了本文所设定的研究效果,如图8(d)所示。 因此,本次研究的倾斜校正图像识别结果如图9 所示。

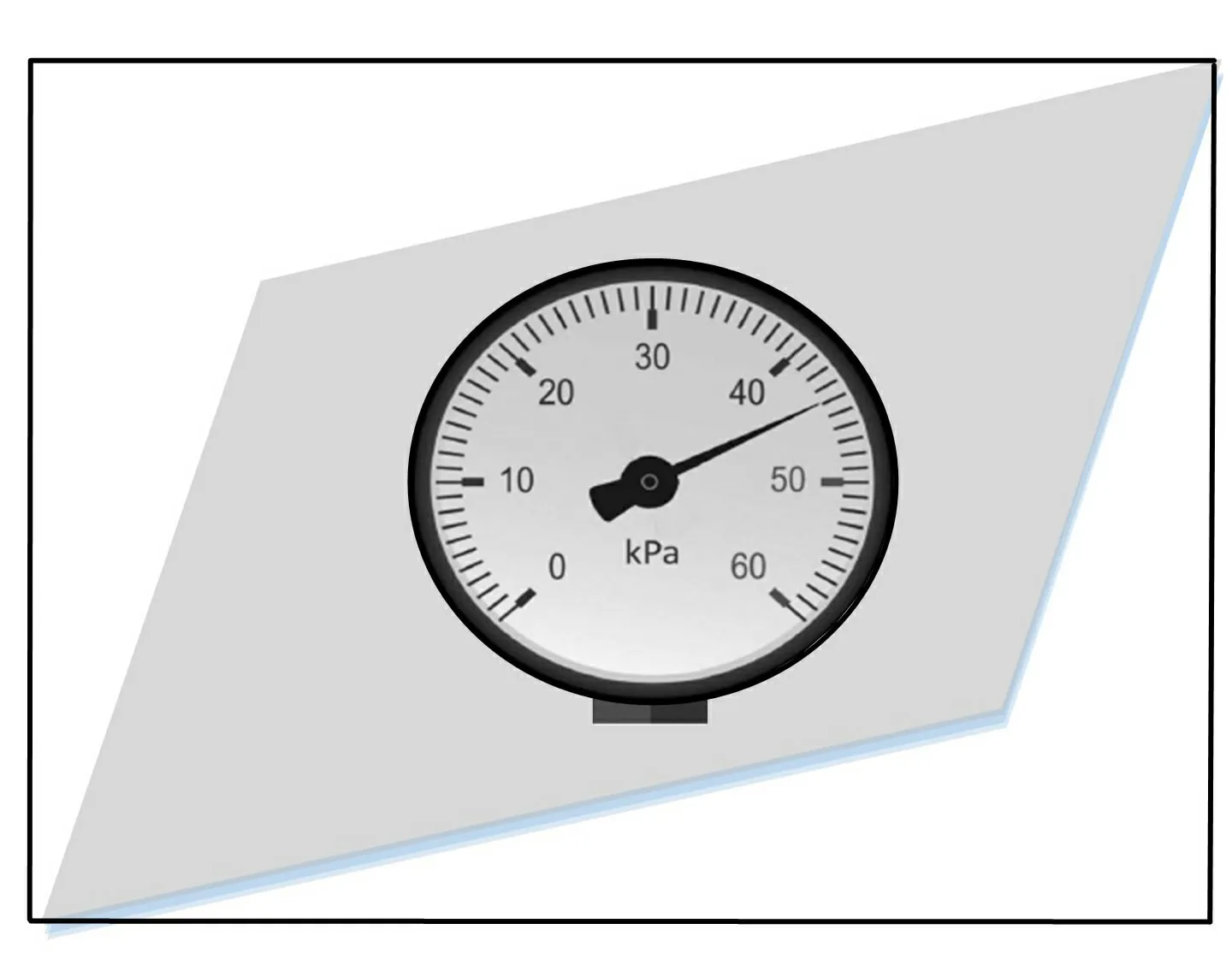
图9 倾斜校正图像识别结果图Fig.9 Image recognition results of tilt correction

由图8 可知,虽然倾斜校正处理后的图像依旧存在些许模糊,但校正处理后的图像特征与校正前相比清晰度、精确度均更高,不影响后续自动识别。由此可见,基于Freeman 链码改进图像处理算法能有效地分析指针式仪表图像倾斜问题并对其进行校正,避免了单一的图像水平倾斜所造成的指针式仪表识别缺陷。

3.2 校正图像识别验证的差异比较

通过上述图像校正处理后,再次对校正后的图像进行示数识别处理。 本文研究的重点是基于Freeman 链码改进图像处理算法的线性指针式仪表识别。

相较于霍夫变换算法,本文提出的基于Freeman链码改进图像处理算法在指针式仪表的应用中的性能更好。 在图9 的基础上,分别比较了人工识别与基于Freeman 链码改进图像处理算法识别基础上的指针式仪表的周长占比情况,如图10 所示。

由图10 可以看出:相较于人工识别而言,基于Freeman 链码改进图像处理算法识别的指针式仪表的周长占比误差相对更低,在可接受范围内波动。

4 结论

综上所述,圆形、优弧或者劣弧是相对常见的指针式仪表的3 种刻度线,工业中常见的是圆形和方形。但从理论角度而言,上述几种指针式仪表的刻度线在经数字化处理之后,均可被视作以指针中心为圆心、以中心点到刻度线的距离为半径的圆形。 本研究在前期研究的基础上,综合考虑了不同情况下指针式仪表图像获取中可能发生的各种问题,并提出了基于Freeman 链码改进图像处理算法的识别方法,实现了对图像倾斜问题的校正与识别,最终验证了指针式仪表示数识别的可靠性,以及Freeman 链码改进图像处理算法的高效性和普适性。