一种新压缩顶点链码

魏 巍，段晓东，刘勇奎，郭 晨

(1.大连民族大学 计算机科学与工程学院，辽宁 大连 116600； 2.大连海事大学 信息科学技术学院，辽宁 大连 116026； 3.大连民族大学 大连市民族文化数字技术重点实验室，辽宁 大连 116600)

一种新压缩顶点链码

魏 巍1,2,3，段晓东1,3*，刘勇奎1，郭 晨2

(1.大连民族大学 计算机科学与工程学院，辽宁 大连 116600； 2.大连海事大学 信息科学技术学院，辽宁 大连 116026； 3.大连民族大学 大连市民族文化数字技术重点实验室，辽宁 大连 116600)

(*通信作者电子邮箱duanxd@dlnu.edu.cn)

链码是一种以较少的数据存储表示线条、曲线和区域边界的编码技术。为进一步提高链码的压缩效率，提出了一种新的压缩顶点链码：改进的正交3方向顶点链码(IO3DVCC)。IO3DVCC将顶点链码(VCC)的统计特征与正交3方向链码(3OT)的方向特征相结合，共设5个码值。码值1将VCC中的1、3组合和3、1组合归并表示，码值2与VCC的对应码值表达相同，码值3与3OT中的码值2表达相同，码值4和码值5分别对应2个连续的新链码码值1和8个连续的VCC码值2。新链码基于Huffman编码，为不定长编码。针对100幅图像的轮廓边界，统计并计算了IO3DVCC与改进的相对8方向Freeman链码(ERD8FCC)、基于算数编码的变长相对四方向Freeman链码(AVRF4)、基于算数编码的正交3方向链码(Arith_3OT)、压缩VCC(CVCC)和改进的CVCC(ICVCC)6种链码各码值出现的概率、平均码值表达能力、平均码长和链码效率。实验结果表明，IO3DVCC效率最高。针对随机选择的20幅轮廓边界图像，统计并计算了IO3DVCC、Arith_3OT和ICVCC3种链码表达的总码数、二进制总位数，以及相对于8方向Freeman链码的压缩比率。实验结果表明，IO3DVCC的压缩效果最好。

链码；Huffman编码；图像边界；链码效率；压缩

0 引言

链码是一种表示线条、曲线和图像边界区域的常用编码技术，它由一系列固定方向和长度的小直线段组成。在表示图像边界轮廓时，按照定义好的编码规则对轮廓上的像素点进行表达和存储。由于链码编码简单，操作方便，因此在图像识别等领域应用广泛。

最直观的链码是Freeman[1]在1961年提出的8方向Freeman链码(8-Direction Freeman Chain Code, 8DFCC)和4方向Freeman链码(4-Direction Freeman Chain Code, 4DFCC)。8DFCC基于边界像素8连通的原理，码值由Σ(F8)={σ|0,1,2,3,4,5,6,7}组成，其中每一码值σ∈Σ表示与X轴正向呈45°×σ角，如图1所示。4DFCC基于边界像素4连通原理，码值由Σ(F4)={σ|0,1,2,3}组成，其中每一码值σ∈Σ表示与X轴正向呈90°×σ角，如图2所示。Freeman链码以图像边界轮廓的方向为依据，因此8DFCC和4DFCC均具有明显的方向性。

图1 8DFCC示例

图2 4DFCC示例

1999年，Bribiesca[2]提出了目前使用非常广泛的顶点链码(VertexChainCode,VCC)。与Freeman链码不同，VCC是通过标记图像边界轮廓像素的顶点数目表示的。VCC的码值由Σ(VCC)={σ|1,2,3}组成，码值1表示单独的像素顶点，通常在边界像素处出现；码值2表示连续的两个像素顶点，用来表示连续的像素；码值3表示将有3个像素顶点聚集在一起，常在边界像素方向改变处出现，如图3所示。

图3 VCC示例

正交3方向链码(OrThogonal3-directionchaincode, 3OT)[3]的码值由Σ(3OT)={σ|0,1,2}组成。其中：码值0表示后继链码与前续链码码值方向相同；码值1表示链码前进方向发生改变，同时与其前续相邻的链码码值改变的变化方向不同；码值2表示链码前进方向发生改变，但与其前续相邻的链码码值改变的变化方向相同。如图4所示。

图4 3OT示例

由图1、图2和图4可以看出，8DFCC、4DFCC和3OT链码在表示图像边界轮廓时具有明显的方向性，而由图3可以发现VCC是通过统计顶点的个数来组成链码的。这些链码对图像轮廓的几何形状均有很好的表示，但在存储时，往往受限于码值长度，导致链码存储占据较大的空间。因此，在后续研究中提出了对这些链码的改进方案。每种新提出的链码均会在一定程度上提高码值平均表达能力，降低链码平均长度，提高链码整体压缩效率。本文将VCC的统计特征与正交3方向链码的方向特征相结合，针对VCC提出了一种新的压缩链码。进一步，对所提的新链码进行改进，大幅提高了链码的压缩效率。

1 链码的改进

1.1 改进的Freeman链码

2001年，刘勇奎[4]基于8DFCC提出了角度差Freeman链码(AngleDifferencesFreemanChainCode,ADFCC)。ADFCC的码值由Σ(ADFCC)={σ|0,1,2,3,4,5,6,7}组成，分别表示码值的角度差为0°、±45°、±90°、±135°和 180°。ADFCC应用Huffman编码，对图像中的数字曲线和边界轮廓进行了统计，对边界中最常出现的像素相邻情况分配较少的二进制位表示，从而相对8DFCC压缩比率有很大提高。

2007年，Zahir等[5]基于8DFCC和ADFCC，提出了改进的相对8方向Freeman链码(EnhancedRelative8-DirectionFreemanChainCode,ERD8FCC)。ERD8FCC的码值由Σ(ERD8FCC)={σ|F,FL,L,BL,B,BR,R,FR,X,Y}组成，其中每一码值均表示当前像素相对于其前续像素的位置关系：F表示当前像素位于前续像素的前方(Front)，FL表示左前方(FrontLeft)，L表示左方(Left)，BL表示左后方(BackLeft)，B表示后方(Back)，BR表示右后方(BackRight)，R表示右方(Right)，FR表示右前方(FrontRight)，X表示连续的10个F，Y表示连续的5个F。同ADFCC类似，ERD8FCC也通过Huffman编码得到不等长的码值表达，相比于ADFCC，对图像中连续的码值合并为一个新的码值。在图像出现连续F码值较多的情况下，能很好地降低F码值出现的概率，同时增加X、Y码值出现的概率。由于X、Y码值的二进制长度小于对应连续F码值所需的二进制长度，因此能够减少了链码二进制总长度，提高压缩效果。

2013年，李灵华等[6]基于4DFCC提出了基于算数编码的变长相对四方向Freeman链码(ArithmeticencodingVariable-lengthRelative4-directionFreemanchaincode,AVRF4)。AVRF4的码值由Σ(AVRF4)={σ|0,1,2,3,4}组成，相比4DFCC新增了码值4。AVRF4变4DFCC的绝对方向为相对方向，码值0表示后续像素与当前像素方向相同，码值1表示后续像素相对当前像素方向向左改变，码值2表示方向向后改变，码值3表示向右改变，码值4表示8个连续的码值0组合。

1.2 改进的3OT链码

2009年，Sánchez-Cruz等[7]基于3OT链码提出了基于算数编码的正交3方向链码(Arithmeticcodingappliedto3OTchaincode,Arith_3OT)。Arith_3OT的码值由Σ(Arith_3OT)={σ|0,1,2,3,4,5}组成，码值0、1、2与3OT的相同，新增的码值3、4、5是基于码值方向的统计，码值3与码值4分别表示5个连续的码值0和1，码值5表示连续的3OT码值0110组合。

1.3 改进的VCC链码

2007年，Liu等[8]对VCC进行改进，提出了压缩VCC(CompressedVCC,CVCC)。CVCC的码值由Σ(CVCC)={σ|1,2,3,4,5}组成，基于Huffman编码对VCC定义了码值进行了新增和改进，其中码值1对应VCC的码值2，码值2对应VCC的码值1、3组合，码值3对应3、1组合，码值4和5分别对应VCC的码值1和3。实验表明，CVCC的压缩比率和链码效率远远高于VCC。

2014年，魏巍等[9]对压缩链码CVCC进一步改进，得到了改进的CVCC(ImprovedCVCC,ICVCC)。ICVCC的码值由Σ(ICVCC)={σ|1,2,3,4,5,6}组成，链码在CVCC的基础上，新增了一个码值6用来表示CVCC中连续的9个码值2的组合。ICVCC与CVCC的对应关系如表1所示。实验表明，其链码效率和压缩比率要高于压缩的VCC的。

表1 ICVCC与VCC的对应关系

除了对常用链码进行改进，研究者尝试应用多种方式提高链码的压缩效率。2015年，Žalik等[10]提出一种新的无损压缩链码方法：基于游程编码、动态窗口等压缩方式对链码二进制进行压缩。2016年，Žalik等[11]又提出采用基于Move-To-Front变换(Move-To-FrontTransformation,MTFT)和Burrows-Wheeler变换(Burrows-WheelerTransform,BWT)等字符变换技术，结合游程编码方法对链码进行压缩，取得了较好的压缩效果。

2 新压缩VCC

2.1 正交3方向VCC

正交3方向链码及其改进链码的共同特点是具有明确的方向性。VCC及其优化链码虽没有明显的方向性，但通过逐一统计边界像素的顶点个数完成编码过程。本文将3OT链码的方向特征与VCC的像素统计特征相结合，提出了一种新的链码：正交3方向VCC(Orthogonal3-DirectionVCC,O3DVCC)。

O3DVCC共3个码值：码值1表示当前链码与之前最近发生方向改变的码值对应的方向不同；码值2同VCC的码值2，表示方向没有改变；码值3表示当前链码与之前最近发生方向改变的码值对应的方向相同。O3DVCC需要一个参考方向，通常将遍历的第1个像素方向定义为参考方向，后续码值均相对于前续的码值进行定义。图5给出了用O3DVCC表示图像边界的示意，其中位于像素格子内的链码表示是VCC，位于像素格子外围带方向箭头的表示为O3DVCC。

O3DVCC将链码的方向特征与统计特征进行了融合，其中方向特征是相对的，统计特征是绝对的。由图5不难发现，应用VCC表示的链码为1313131时，对应的O3DVCC链码表示为1111111；应用VCC表示的链码为3131时，对应的O3DVCC链码也表示为1111；VCC中的码值2与O3DVCC中的码值2保持一致。可以看出，O3DVCC将VCC中的码值1、3组合和3、1组合统一归并为带有方向性质的码值1。这为进一步压缩O3DVCC链码奠定了基础。

图5 O3DVCC示例

若以VCC为基准链码，其转换为O3DVCC的算法如下：

/*数组V[]存放VCC码值*/ /*数组N[]存放O3DVCC码值*/Vertex2New(V[]) { /*reference_section为参考段码值*/reference_section=0; /*i为O3DVCC码长*/i=1;WhileV[i]NotNullDo{If(V[i] == 2‖reference_section==0)Then{N[i]==V[i];If(V[i]～=2)Thenreference_section=V[i];

}

Else

{If(reference_section==V[i] )ThenN[i]=3;

ElseN[i]=1;reference_section=V[i];

}

i=i+1;

}

}

同理，O3DVCC也可以转换为VCC，其算法如下：

/*数组V[]存放VCC码值*/ /*数组O[]存放O3DVCC码值*/O2Vertex(O[]) {i=1;reference_section=0; /*reference_section为参考段码值*/WhileO[i]NotNullDo{If(O[i] == 2‖reference_section== 0)Then{V[i]==O[i];

If(V[i]～=2)Thenreference_section=V[i];

}

Else

{If(reference_section+V[i]== 4 )Then{N[i]=1;reference_section=1;}

Else{N[i]=3;reference_section=3;}

}

i=i+1;

}

}

本文应用O3DVCC对100幅图像进行了概率统计，并基于Huffman编码计算了O3DVCC每一码值的二进制编码，如表2所示。

根据表2，可知码值1和码值2的概率较为近似，远远超过了码值3出现的概率。这意味着图像轮廓中出现相对方向不同向变化的概率和方向不发生变化的概率要远大于出现相对方向同向变化的概率。基于该统计，可以对O3DVCC链码进一步改进。

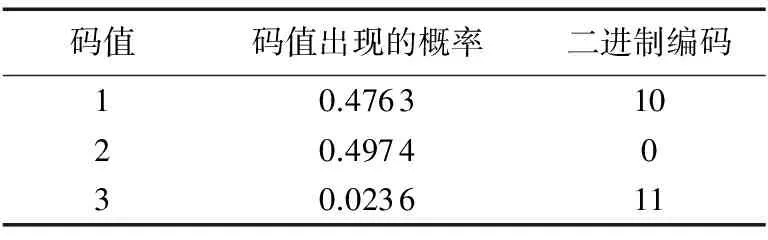
表2 O3DVCC码值概率与二进制编码

2.2 改进的O3DVCC

由于O3DVCC中码值1和码值2占有很大比例，因此对存在连续的码值1和连续的码值2进行改进，必定能够提高链码的压缩效率。在O3DVCC的基础上，新增了2个码值，分别表示M个码值1和N个码值2，定义该链码为改进的O3DVCC(ImprovedO3DVCC,IO3DVCC)。对100幅图像的边界轮廓进行了统计，并基于Huffman编码为M=2，3，…，10且N=2，3，…，10共81种组合中每一组合的链码进行了二进制码值编码，同时计算了每一组合的链码平均表达能力，链码平均码长和链码的效率，如表3所示。

表3 IO3DVCC不同M、N组合对应的效率统计

由表3可知，当M=2、N=8时链码的效率是最高的，为0.932 3。因此，定义IO3DVCC为5个码值，前3个码值与O3DVCC一致，码值4定义为连续2个码值1，码值5定义为连续8个码值2。表4给出了IO3DVCC与O3DVCC的对应关系以及其在100幅测试图像中出现的概率和具体的二进制编码。

再次，形成新市场。一方面，要通过促进传统五大需求“吃穿住行用”升级，来形成新市场；另一方面，要通过培育新五大需求“学乐康安美”（学习需求、快乐需求、健康需求、安全需求、美丽需求），来形成新市场。

表4 IO3DVCC与O3DVCC的对应关系

3 新压缩VCC与其他链码的比较分析

3.1 链码评价的方法

评价链码的主要指标是链码效率[12]，其公式可表示为：

e=c/l

(1)

其中：e表示链码的效率；c代表码值平均表达能力；l代表平均码长。

码值的表达能力指码值所能表示的区域边界(或数字曲线)的像素长度的平均值，如图6所示。

图6 码值表达能力

8DFCC链码中码值0、2、4、6的表达能力为1个像素长度；码值1、3、5、7的表达能力为2个像素长度。4DFCC和VCC的所有码值表达能力均为1个像素长度。

链码的平均表达能力可表示为：

(2)

其中：ci为链码中某一码值的表达能力；pi为该码值出现的概率。

链码的平均码值长度，对于定长链码，其链码平均码长即为表达每位链码所需的bit。如，8DFCC链码由8个码值，每个码值用固定的3个bit进行表示，因此其平均码长为3bit/码。

(3)

其中：li为链码中某一码值表达所占的bit数；pi为该码值出现的概率。

3.2 实验比较与分析

通常，改进链码的压缩效果要好于被改的链码。为了验证IO3DVCC的有效性，本文基于100幅图像将IO3DVCC的平均表达能力c，平均链码长度l和链码效率e，与改进的8方向Freeman链码ERD8FCC和改进的4方向链码AVRF4，改进的3OT链码Arith_3OT，以及改进的VCC链码CVCC和ICVCC进行了比较，并给出了这些链码的码值出现概率和二进制编码表示，如表5所示。

表5 不同链码的性能对比

由表5可以发现:6种链码中平均表达能力最强的是Arith_3OT链码，为1.991 5像素长度;其次是ERD8FCC，为1.750 9像素长度;第三是ICVCC链码，为1.543 6像素长度;第四是本文提出的IO3DVCC链码，为1.537 6像素长度;CVCC与AVRF4的平均表达能力分别为1.308 0像素长度和1.144 8像素长度。

6种链码中，CVCC的平均链码长度最短，为1.567 2/码，其次是IO3DVCC，为1.649 3/码，第三是ICVCC为1.780 7/码，后续依次是AVRF4为1.923 4/码，ERD8FCC为2.108 0/码，Arith_3OT为2.266 5/码。

在这些链码比较中，效率最高的是本文提出的IO3DVCC，为0.932 3；其次是Arith_3OT，为0.878 7；第三是ICVCC；CVCC和ERD8FCC较为接近，分别是0.834 6和0.830 6；AVRF4最少，为0.595 2。

分析原因，IO3DVCC的平均表达能力和链码长度对比其他链码虽然并非最优，但均排在前列。Arith_3OT的平均表达能力最强，但其平均链码长度过长，排在6种链码的最后，因而其效率并非最高。ICVCC链码的平均表达能力和链码长度排名均靠前，因此其效率较高。CVCC的平均链码长度较短，虽然其平均表达能力不高，但其效率较高。

进一步检验IO3DVCC的压缩效果，从100幅图像样本中随机抽取20幅，将IO3DVCC与上述链码效率较高的Arith_3OT和ICVCC以8DFCC为基准进行比较。所选的20幅图像轮廓边界如图7所示。各图像的尺寸如表6所示。针对这20幅图像，分别统计这四种链码相对每幅图像轮廓的总码数和所占二进制总数，以及相对于8DFCC的压缩比率，如表7所示。

图7 图像轮廓边界

图像尺寸总像素数图像尺寸总像素数宝宝193×17533775路由器300×30090000豹子350×27495900驴147×17024990贝壳211×15031650螃蟹350×23180850茶杯153×15022950酒瓶251×21152961房子662×514340268小轿车375×24993375枫叶343×300102900雨伞422×300126600海贼王200×15030000乌龟454×300136200汽车447×300134100椅子436×330143880警帽221×22048620苹果220×22048400老鼠275×36199275板凳278×22061160

链码存储的空间大小与码值数和链码的码值长度相关。相同码值数，码值长度多的链码势必要比码值长度少的更占用空间。表7中，Arith_3OT、ICVCC和IO3DVCC的码值数相比8DFCC均有压缩，其中Arith_3OT的总码数最少，其次是ICVCC，而IO3DVCC相对较多。然而，由于Arith_3OT的链码长度均多于ICVCC和IO3DVCC，因此其所占存储空间并非最少。IO3DVCC的码值总数与ICVCC较为接近，但由于其链码长度少于ICVCC和Arith_3OT，因此所占存储空间最少。

表7 各链码相对图像轮廓链码的总码数与二进制总位数，以及相对于8DFCC的压缩比率

从链码效率角度分析，链码效率越高，单位像素长度对应的码值表达能力越强，相对于同一种链码的压缩比率越高，压缩效果越明显。由表7可知，在Arith_3OT、ICVCC和IO3DVCC链码相对于8DFCC的压缩比率比较中，IO3DVCC的压缩比率是最明显的，其次是Arith_3OT，最后是ICVCC，这与表5给出的链码效率是完全一致的。

进一步分析，链码IO3DVCC、Arith_3OT、ICVCC均是变长编码，且都采用了Huffman编码方式。Arith_3OT将连续码值合并生成新码值，其码值3、4均是对连续相同3OT码值表示，码值5则是对0110特定的组合进行表示，结果Arith_3OT链码的压缩效果明显优于3OT。IO3DVCC的码值4表达的是连续2个O3DVCC码值1，O3DVCC的码值1又将CVCC的码值2和码值3进行了归并表示，其分别对应VCC的码值1、3和3、1组合。IO3DVCC的码值5表达的是连续的8个码值2，而码值2又与O3DVCC的码值2和VCC的码值2是相同的，这同ICVCC链码的码值6表示连续的9个VCC码值2相似。由此不难发现，IO3DVCC相对于ICVCC对CVCC进一步优化。ICVCC重点对CVCC中连续的码值2定义了一个新的码值，IO3DVCC不仅对CVCC连续的码值2进行了新的定义，还对CVCC的码值2和码值3进行了归并表示，因此IO3DVCC的压缩效果必定优于ICVCC和CVCC。这类通过概率统计出连续相同码值出现的概率，进而通过定义新码值对这些连续相同码值进行表示的方法，从本质上均是对各自原始链码的优化，因此其效率必定高于所对应的原始链码。

4 结语

本文将VCC的统计特征和正交3方向链码的方向特征进行融合，提出了一种改进的O3DVCC。基于100幅图像样本，统计了IO3DVCC、ERD8FCC、AVRF4、Arith_3OT、CVCC和ICVCC等链码各码值出现的概率，给出了码值的二进制编码表示，计算了码值平均表达能力、平均长度和链码效率，结果显示IO3DVCC链码的效率最高。在后续的实验验证中，统计了链码效率计算排名靠前的I3ODVCC、Arith_3OT和ICVCC在表达20幅随机图像样本中的码值总数、二进制总位数和相对于8DFCC的压缩比率，结果表明，IO3DVCC压缩效果最好。本文方法存在的不足是编码与解码方式较为复杂，时间消耗较大，因此，下一步的研究工作是对链码进一步改进，降低时间复杂度。

)

[1]FREEMANH.Ontheencodingofarbitrarygeometricconfigurations[J].IRETransactionsonElectronicComputers, 1961,EC-10(2): 260-268.

[2]BRIBIESCAE.Anewchaincode[J].PatternRecognition, 1999, 32(2): 235-251.

[3]SANCHEZ-CRUZH,BRIBIESCAE,RODRIGUEZ-DAGNINORM.Efficiencyofchaincodestorepresentbinaryobjects[J].PatternRecognition, 2007, 40(6): 1660-1674.

[4] 刘勇奎.Freeman链码压缩算法的研究[J].计算机学报,2001,24(12):1294-1298.(LIUYK.ResearchonthecompressionalgorithmforFreemanchaincode[J].ChineseJournalofComputers, 2001, 24(12): 1294-1298.)[5] ZAHIR S, DHOU K. A new chain coding based method for binary image compression and reconstruction [EB/OL]. [2016- 10- 20]. http://www.eurasip.org/Proceedings/Ext/PCS2007/defevent/papers/cr1221.pdf.

[6] 李灵华,刘勇奎.Freeman 四方向链码压缩率提高的方法研究[J].计算机工程与设计,2013,34(3):1132-1136.( LI L H, LIU Y K. Study on methods for improving compressibility of 4-direction Freeman chain code [J]. Computer Engineering and Design, 2013, 34(3): 1132-1136.)

[7] SANCHEZ-CRUZ H, RODRIGUEZ-DIAZ M A. Coding long contour shapes of binary objects [C]// Proceedings of the 2009 14th Iberoamerican Conference on Pattern Recognition, Image Analysis, Computer Vision, and Applications, LNCS 5856. Berlin: Springer, 2009: 45-52.

[8] LIU Y K, WEI W, WANG P J, et al. Compressed vertex chain codes [J]. Pattern Recognition, 2007, 40(11): 2908-2913.

[9] 魏巍,刘勇奎,段晓东,等.基于Huffman编码的改进压缩链码[J].计算机应用,2014,34(12):3565-3569.( WEI W, LIU Y K, DUAN X D, et al. Improved compression vertex chain code based on Huffman coding [J]. Journal of Computer Applications, 2014, 34(12): 3565-3569.)

[10] ŽALIK B, MONGUS D, LUKACN. A universal chain code compression method [J]. Journal of Visual Communication & Image Representation, 2015, 29(C): 8-15.

[11] ŽALIK B, MONGUS D, ŽALIK K R, et al. Chain code compression using string transformation techniques [J]. Digital Signal Processing, 2016, 53(C): 1-10.

[12] 刘勇奎,魏巍,郭禾.压缩链码的研究[J].计算机学报,2007,30(2):281-287.(LIU Y K, WEI W, GUO H. Research on compressed chain code [J]. Chinese Journal of Computers, 2007, 30(2): 281-287.)

This work is partially supported by the National Natural Science Foundation of China (61672132, 51579024), the Science Research Project of Liaoning Provincial Department of Education (L2014546), the Liaoning Province Science and Technology Plan (2013405003), the Fundamental Research Funds for the Central Universities (DC201502030408, DC201501025).

WEI Wei, born in 1980, Ph. D., associate professor. His research interests include computer graphics, pattern recognition.

DUAN Xiaodong, born in 1963, Ph. D., professor. His research interests include intelligent computing.

LIU Yongkui, born in 1961, Ph. D., professor. His research interests include computer graphics.

GUO Chen, born in 1956, Ph. D., professor. His research interests include virtual reality.

A new compressed vertex chain code

WEI Wei1,2,3, DUAN Xiaodong1,3*, LIU Yongkui1, GUO Chen2

(1.SchoolofComputerScienceandEngineering,DalianMinzuUniversity,DalianLiaoning116600,China; 2.CollegeofInformationScienceandTechnology,DalianMaritimeUniversity,DalianLiaoning116026,China; 3.DalianKeyLabofDigitalTechnologyforNationalCulture,DalianMinzuUniversity,DalianLiaoning116600,China)

Chain code is one kind of coding technology, which can represent the line, curve and region boundary with small data storage. In order to improve the compression efficiency of chain code, a new compression vertex chain code named Improved Orthogonal 3-Direction Vertex Chain Code (IO3DVCC) was proposed. The statistical characteristic of the Vertex Chain Code (VCC) and the directional characteristic of the OrThogonal 3-direction chain code (3OT) were combined in the proposed new chain code, 5 code values were totally set. The combination of 1, 3 and the combination of 3, 1 in VCC were merged and expressed by code 1. The expression of the code 2 was the same with the corresponding code value of VCC. The expression of code 3 was the same as the code value 2 of 3OT. Code 4 and code 5 corresponded to the two continuous code value 1 of IO3DVCC and eight continuous code values 2 of VCC respectively. Based on Huffman coding, the new chain code was the indefinite length coding. The code value probability, average expression ability, average length and efficiency of IO3DVCC, Enhanced Relative 8-Direction Freeman Chain Code (ERD8FCC), Arithmetic encoding Variable-length Relative 4-direction Freeman chain code (AVRF4), Arithmetic coding applied to 3OT chain code (Arith_3OT), Compressed VCC (CVCC), and Improved CVCC (ICVCC) were calculated aiming at the contour boundary of 100 images. The experimental results show that the efficiency of I3ODVCC is the highest. The total code number, total binary bit number, and compression ratio relative to the 8-Direction Freeman Chain Code (8DFCC) of three kinds of chain codes including IO3DVCC, Arith_3OT, and ICVCC were calculated aiming at the contour boundary of 20 randomly selected images. The experimental results demonstrate that the compression effect of IO3DVCC is the best.

chain code; Huffman coding; image boundary; efficiency of chain code; compression

2016- 12- 07;

2017- 03- 02。

国家自然科学基金资助项目(61672132,51579024)；辽宁省教育厅科学研究项目(L2014546)；辽宁省科技计划项目(2013405003)；中央高校基本科研业务费专项资金资助项目(DC201502030408，DC201501025)。

魏巍(1980—)，男，河南安阳人，副教授，博士，主要研究方向：计算机图形学、模式识别； 段晓东(1963—)，男，吉林辽源人，教授，博士，主要研究方向：智能计算； 刘勇奎(1961—)，男，辽宁沈阳人，教授，博士，主要研究方向：计算机图形学； 郭晨(1956—)，男，江苏如东人，教授，博士，主要研究方向：虚拟现实。

1001- 9081(2017)06- 1747- 06

10.11772/j.issn.1001- 9081.2017.06.1747

TP391.9

A