人工智能与雷达图相结合的配电网运维分析研究
2021-09-08冯建伟王联智吴海杰
冯建伟,王联智,谢 敏,吴海杰,孟 超
(南方电网海南数字电网研究院有限公司,海南 海口 570100)
0 引言
随着我国社会主义建设步伐的加快,各行各业的发展都需要电力的支持[1-3]。 为了满足电力需求,配电网的规模日益壮大,其日常运行维护所需的人力、物力以及资金都不断增加。 传统的配电网运维检测方式已经难以支持配电网运维所需。 近几年越来越火热的人工智能则为配电网的检测提供了解决方案[4-6]。
本研究提出将人工智能与雷达图相结合的解决方案,并将其应用于配电网的运维分析。 该研究为我国配电网运维问题的解决及后续发展提供参考。
1 K-means 聚类分析法与雷达图的综合评价法
K-means 聚类分析法计算方法简单、运行速度较快,在大数据中被广泛使用。 但是K-means 算法同样存在十分明显的缺陷[7-8]。 K-means 聚类分析法的结果很不稳定,容易陷入局部最佳的结果。 K-means 聚类分析法使用随机选定法对初始聚类中心进行选择,并通过不断迭代以达到算法收敛的目的,所以初始聚类中心点的选择对聚类分析法的最终结果有很大程度的影响。 在进行聚类分析之前,需要确定K值。 在使用K-means 聚类分析法前,必须充分了解所研究的数据。 然而,在一般情况下,使用者对于数据可能没有足够的了解,因此对于K值的选择具有一定的困难。
本文在数据密度思想的基础上,对K-means 聚类分析法进行初始点选择。 选择过程如下。 首先,对数据之间的平均密度进行计算,并将其中密度最大的1个点作为首个初始聚类中心点。 随后,将数据中距离首个初始聚类中心点最远且密度大于n的点作为第二个聚类中心点。 最后,对其余数据进行选择:将距离上文中2 个点最大的最小距离选作第三个聚类中心点,直到选择出K个聚类中心点。 对于数据集中的数据距离以及数据密度,可通过式(1)和式(2)进行计算。

式中:fden(xi)为数据对象xi与数据对象xj间的密度;M(D)为数据间的欧式距离;距离u( )是一个定义的函数,当自变量大于等于0 时u( )= 1,否则u( )= 0。
对聚类分析法中的聚类个数K值进行选择的方法有多种。 本文主要采用了轮廓系数和误差平方的方法,即手肘法。 手肘法的核心为误差平方和(sum of the squared errors,SSE),计算如式(3)所示。

式中:ci为划分聚类i;p为ci中的一个样本点;mi为ci的质心。


式中:b(p)为不同簇之间的梳理程度;a(p)为簇内不同个体间的紧密程度;s(p)为对象p的轮廓系数,处于[-1,1]之间,与1 越接近则聚类分析效果越好。
SSE-K 折线图夹角计算如图1 所示。
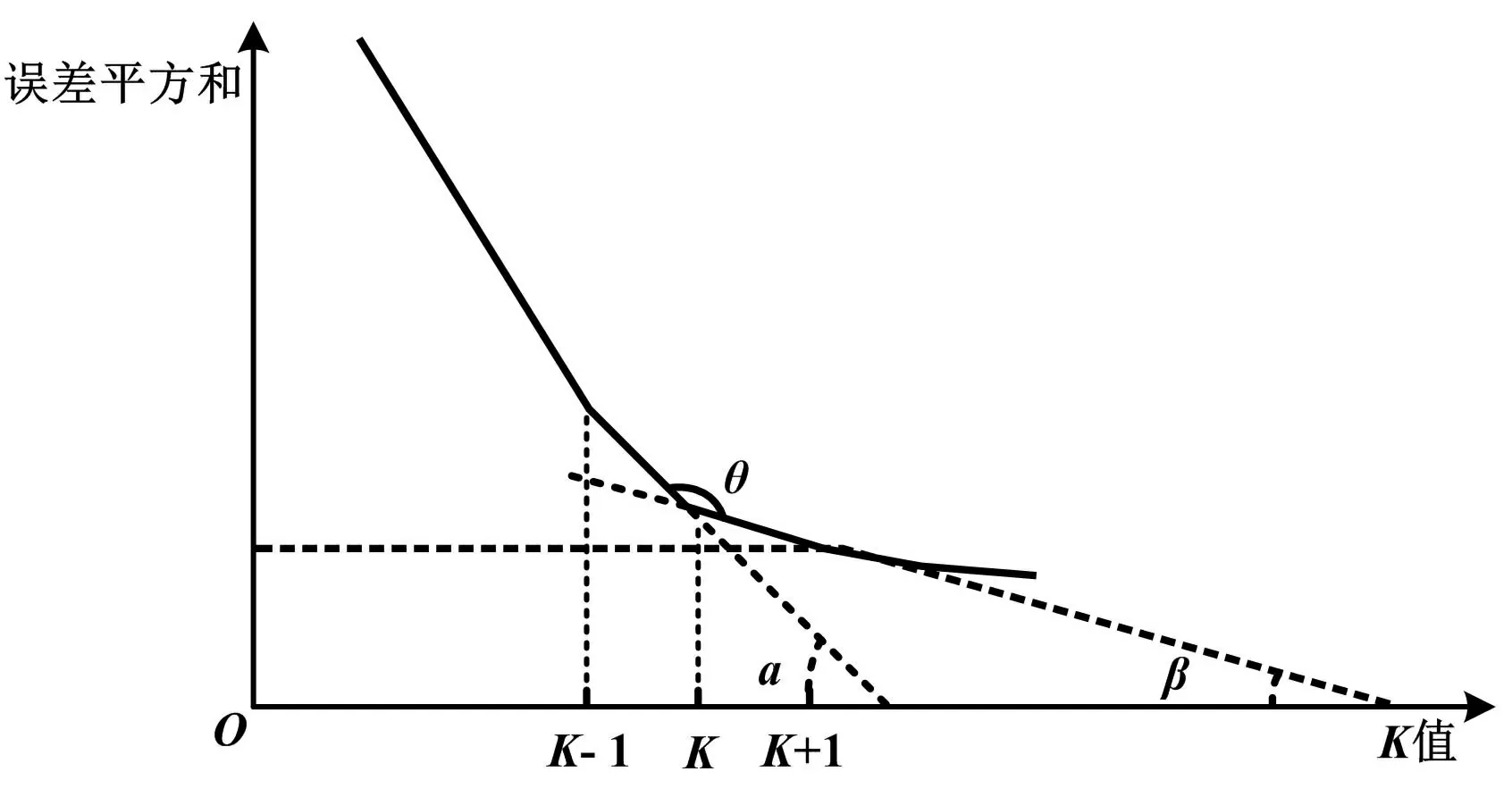
图1 SSE-K 折线图夹角计算示意图Fig.1 Schematic diagram of angle calculationof SSE-K line chart
聚类分析法用于大量数据以及多维度数据处理时,其强大的运算能力可以为配电网中的共性问题解决起到强有力的辅助作用。 然而,该方法在配电网运维指标评价问题中,也存在诸多不足。 例如在对各个地方的配电网运维情况进行评价时,因为聚类分析法不能进行定量化的分析,从而无法对各地的配电网运维水平进行优劣排序。 其次,聚类分析法不能直观展示聚类的结果,致使聚类的结果不便于理解。
为弥补聚类分析法在定量分析以及可视化这2 个方面的不足,本文在聚类算法的基础上结合了雷达图,能够进行大量数据挖掘,具有定量评价及可视化的能力。 本文所采用的综合评价法流程如图2 所示。
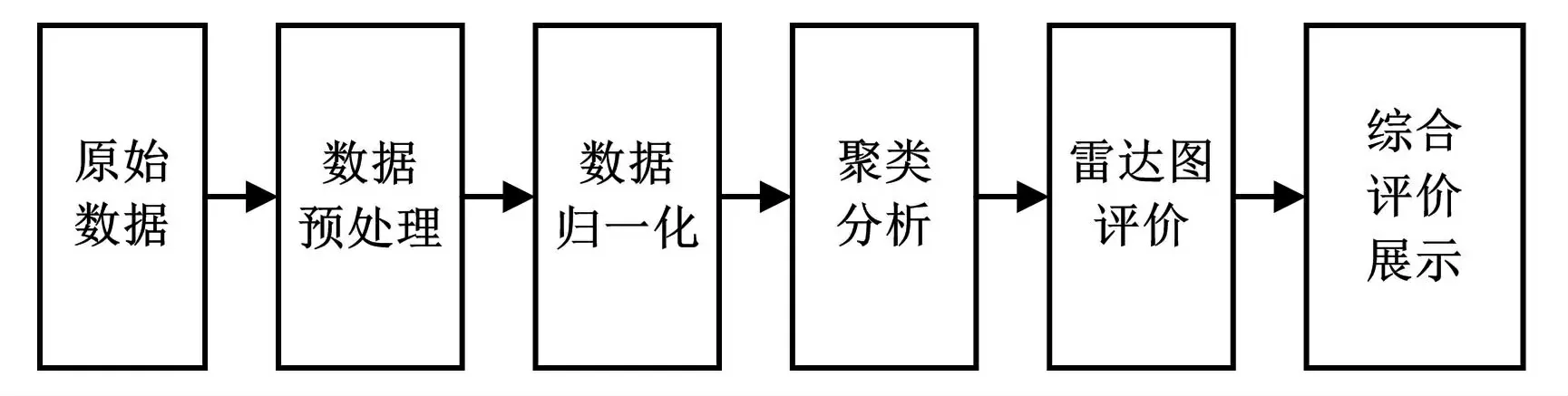
图2 综合评价法流程图Fig.2 Flowchart of comprehensive evaluation method
2 基于改进雷达图评价方法的配电网运维评价
2.1 传统雷达图评价及缺陷分析
雷达图可以将需要评价的对象用一个二维平面图表示。 该二维图像与雷达极为相似,因而得名雷达图[9-10]。 雷达图法是一种广泛应用于多个领域的综合性评价方法,尤其适用于多属性对象全局与整体的评价。 在使用雷达图对对象进行评价时,可根据所需要评价对象的指标将一个单位圆划分为m份。 在划分好的单位圆中,将每个区域划分线作为轴线,并标示出代表该区域的指标,随后将各个点沿顺(逆)时针的顺序进行连接,可得到如图3 所示的雷达图。
图3 雷达图示意图Fig.3 Radar chart diagram
绘制雷达图后,需要提取雷达图的特征量。 将周长与面积作为雷达图的特征量,并分别使用Lj与Sj对2 项特征量进行表示。 雷达图的相对面积大小为:

式中:Smax为所有雷达图中的面积最大值。
设vj2为各项指标的均衡程度,若雷达图与圆越接近,那么所对应的系数则越大,其代表的研究对象发展也就越均衡。vj2的表达式如式(6)所示。

本文构造了评价函数,对该系统进行评价,并可根据评价的结果进行优劣排序。 评价函数如式(7)所示。

雷达图具有使用简单、形象直观等优点,但依旧存在一些不足。 首先,雷达图的评分结果并不唯一。 这是因为雷达图的相邻轴之间使用的是直线连接,所以当轴线的排列顺序发生变化时,其雷达图结果也会随之发生变化,进而影响到最终的评价结果。 由此可见,雷达图的轴线排列顺序会影响到雷达图的均衡度与面积,不具有唯一性。 其次,雷达图评价不能直接使用。本文中的配电网运维指标为负向指标,而雷达图默认为正向指标,因此需要对雷达图进行改进。
2.2 雷达图改进方法
改进雷达图如图4 所示。

图4 改进雷达图示意图Fig.4 Schematic diagram of improved radar chart

经过式(8)的处理之后,所有运维指标都变成了逆向指标。 逆向指标相对面积大小提取方法如式(9)所示。

式中:Sj为评级对象j雷达图的面积;vj1为雷达图相对面积的大小;Smin为全部雷达图面积的最小值。
由于式(9)所得到的vj1与vj2变化趋势相同,都是越接近1 评分越高,而评价函数维持不变,依旧采用式(7)作为评价函数。 计算vj1、vj2时,Smin选取非零的最小面积。
3 试验研究与分析
为了验证本方法对配电网运维情况分析的有效性,选取了某地区的115 个配电网运维数据,并根据9种评价指标进行了综合评价。 对配电网运维数据的SSE 进行计算,绘制SSE-K 折线图,如图5 所示。 当K为5 时,其夹角为152°,是所有夹角中最小的,因此确定此次聚类个数应为5。

图5 SSE-K 折线图Fig.5 SSE-K line chart
利用聚类中心选择法,对选择的配电网指标进行计算,如表1 所示。 将聚类中心分为9 种评价指标,聚类编号1、2、3、4、5 分别对应个数为47、3、35、17、13,所占比例分别为40. 87%、2. 61%、30. 43%、14. 78%、11.30%。 随后将基于密度的随机选择初始聚类中心点法与初始聚类中心点选择法进行对比,并对2 种方法分别进行50 次聚类分析,对比其在不同K值下的轮廓系数平均值。 K-means 与本文算法的平均轮廓系数对比如图6 所示。 由图6 可以看出,基于数据密度的初始聚类中心点选择方法的聚类效果更好。

表1 配电网运维数据聚类分布表Tab.1 Cluster distribution table of operation and maintenance data of distribution network %
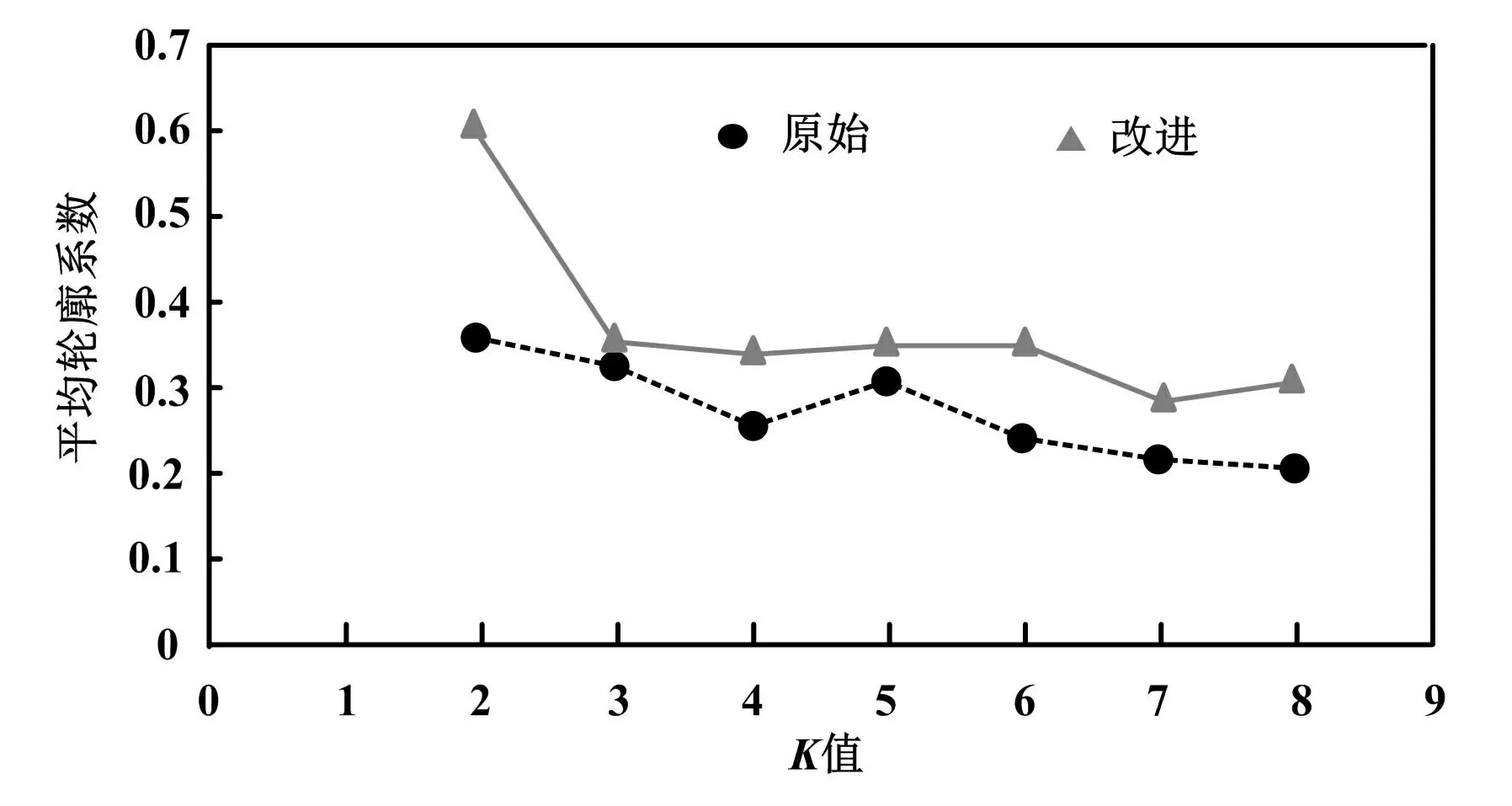
图6 K-means 算法与本文算法的平均轮廓系数对比图Fig.6 Comparison of average contour coefficient between K-means algorithm and the algorithm in this study
将聚类分析法与雷达图评价结果进行整合后,分析配电网运维评价散点,如图7 所示。
以1 分为满分。 通过图7 可以看到:5 种聚类中的聚类3 的评分最好,其评分大部分位于0.5 分之上;聚类2 的评分则最差,集中在0.2 分左右;其余3 种聚类的评价较为相似。 相同的评分结果出现在了不同的聚类结果当中。 这种聚类分析结果与雷达图结果相交叉的现象说明了综合考虑的重要性以及必要性,2 种方法可以起到相互弥补的作用。
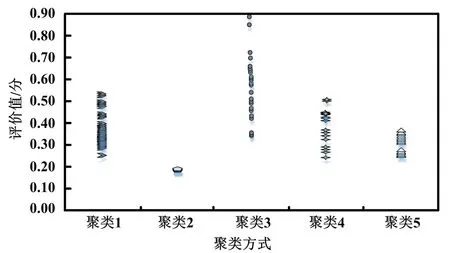
图7 配电网运维评价散点图Fig.7 Scatter diagram of distribution network operation and maintenance evaluation
5 种聚类堆叠雷达图如图8 所示。
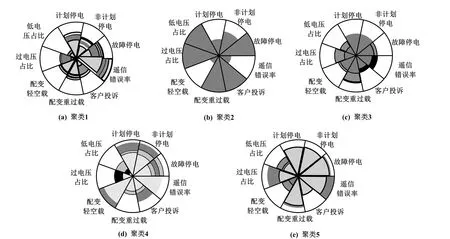
图8 5 种聚类堆叠雷达图Fig.8 Five kinds of cluster stacked radar charts
为了便于比较,将不用分数段的供电公司进行了堆叠雷达图展示。
图8(a)为聚类1 堆叠雷达图。 该地区的9 种评价指标中,遥信错误率是最高的,因此该地区需要对配电网自动化方面的工作进行严格检查,从而降低其遥信错误率。
图8(b)为聚类2 堆叠雷达图。 该地区的9 种评价指标中,过电压占比、低电压占比、故障停电以及客户投诉四项指标均较高,说明了该区域的电压运行水平较差,存在配电网配变储备容量不足以及发生故障后检修不及时等情况,因此可以认为该区域配电网运维水平较差。
图8(c)为聚类3 堆叠雷达图。 该地区的9 种评价指标都较小,说明了该区域的配电网运维水平整体较好。 9 种指标中的配变重过载指标相对其他指标较大,说明了该区域的配变过载问题还需进一步优化。
图8(d)为聚类4 堆叠雷达图。 该地区的9 种评价指标中仅有客户投诉、配变重过载、过电压占比以及低电压占比指标较小,其余指标均较大,说明了该区域配电网故障较多、运维水平较差。
图8(e)为聚类5 堆叠雷达图。 该地区的9 种评价指标中,仅有低电压占比、配变轻空载以及客户投诉指标较小,其余指标较大,说明了该区域配电网故障多、配变储备容量不足、遥信情况较差,运维水平较差。
综上所述,本文所提出的改进K-means 聚类分析法与雷达图的综合评价法可以对配电网中的共性问题进行检测,同时还可以客观地对配电网运维情况进行定量以及可视化的分析。
4 结论
配电网信息数据量的逐年增大,使得传统方法不能及时检出配电网运维中的问题。 为了解决这一问题,本文提出K-means 聚类分析法与雷达图结合的方法,实现配电网运维情况的快速检测。 对配电网的9 种评价指标进行检测评价,并以K-means 聚类分析法与雷达图进行检测,最后通过试验进行验证。 验证结果表明,综合评价法可以对配电网的运维水平进行客观、定量以及可视化的检测。 但是本研究仍存在一些不足,研究选取的数据规模还应进一步扩大,以提高研究的泛用性。
