温度传感器智能故障诊断和容错估计
2021-09-08徐绍龙李学明成正林
徐绍龙,李学明,成正林
(株洲中车时代电气股份有限公司技术中心,湖南 株洲 412001)
0 引言
在自动控制领域中,传感器把被测物理信号转化成电信号,对监控系统的运行至关重要。 当其出现故障时,将给后续的监测、控制、故障诊断等系统带来严重影响[1]。 例如,在机车传动控制系统中,温度是表征设备工作环境与状态的一个重要指标,如牵引变压器油温、牵引变流器水冷系统的入、出水口温度传感器温度、柜体空气温度和牵引电机温度等。 如果温度过高,需对机车进行减功率运行、断主断路器等保护动作,以保证设备的安全运行。 牵引传动系统装置运行环境复杂,腐蚀、温度、湿度以及电浪涌、静电等因素都会影响其运行状态[2]。
安装温度传感器时,接线错误或机车运行过程中的强烈振动,经常会导致传感器故障(如断线、短路、反接等)。 此时,传感器测量值将偏离真实值。 如果测量值比真实值偏高,将导致系统误动作,影响机车的正常运行[3]。 如果测量值比真实值偏低,将导致系统漏动作,对机车设备造成损害。 因此,研究温度传感器的智能故障诊断以及故障工况下的温度估计算法,以估计值代替实际测量值来进行系统保护,具有较高的应用价值。
本文以温度传感器的历史故障数据样本及正常历史数据为基础,提出了一种智能故障诊断和容错估计方法。 通过故障样本特征分析建立传感器故障判断的规则库,并得出故障工况的容错估计方法。 对于不可根据故障样本重构的故障工况,采用传感器的正常历史数据建立传感器测量值的灰色预测模型,从而实现不可隔离故障样本的容错估计。 仿真结果和在列车牵引系统上的现场应用结果均证明了该方法的有效性。
1 温度传感器信号采样电路简介
热电阻(例如PT100)是利用其电阻值随温度的变化而变化这一原理制成的,将温度量转换成电阻量的温度传感器。 温度测量电路通过先给热电阻施加一个已知激励电流再测量其两端电压的方法得到电阻值(电压/电流),并将电阻值转换成温度值,从而实现温度测量[4]。
热电阻与温度测量电路之间有三种接线方式:二线制、三线制[5]和四线制[6]。 由于四线制测量方式不受连接导线的电阻的影响,在现场得到了广泛的应用。绝大多数机车传动系统中也采用了此接线方式。 因此,本文以四线制接法的温度传感器为例,研究其信号采样电路原理、故障诊断及容错估计方法。
典型的温度信号采样原理如图1 所示[7]。
图1 中,PT100 两端通过A1、A2两端接入4.9 mA恒流源,然后温度信号采样电路通过B1、B2得到其差分输入电压Uin。Uin经过电压跟随器生成单端电压信号Uin′,然后进入同相比例运算放大电路生成满足控制单元模数转换器(analog to digital converter,ADC)采样所需的电压信号。

图1 温度信号采样原理图Fig.1 Schematic diagram of temperature signal sampling
若设同相比例运算放大电路的放大倍数为K, 则温度传感器(PT100)采样温度值T与温度信号采样电路输出电压值U之间的关系如式(1)所示。

2 温度传感器智能诊断和容错估计方法原理
传感器原始信号通过信号采样电路后,进入控制单元的智能诊断与容错估计模块。 首先,根据传感器信号采样电路参数对信号有效性进行判断。 若判断正常,则输出传感器信号测量值作为真实值。若判断异常,则进入故障诊断模块。 故障诊断模块根据故障样本规则库中的相关规则和输入信号,判断出当前故障类别。 若故障为可重构类型,则直接计算出传感器信号的重构值作为真实值;反之,则进入灰色预测模块。 灰色预测模块根据正常历史数据对当时测量值进行估计,得出传感器信号的估计值作为真实值。
温度传感器智能诊断和容错估计原理如图2 所示。

图2 温度传感器智能故障诊断和容错估计原理示意图Fig.2 Schematic diagram of intelligent fault diagnosis and fault tolerant estimation of temperature sensor
从图2 可以看出,故障样本规则库创建和规则提取是实现专家诊断的关键。 此外,若故障类别为不可重构故障,则需根据正常历史数据,利用灰色预测理论对传感器信号真实值进行估计。 下面以机车传动系统牵引变流器水冷系统中的入口水温传感器为例,阐述本文提出的算法原理。
2.1 信号有效性判断
根据实际应用经验,机车传动系统牵引变流器水冷系统中的入口水温信号Tin的正常范围为-60~+80 ℃,入口水温信号采样电路的比例运算放大器倍数K为14。 由此可以根据式(1)算出入口水温采样电路输出电压U的理论值正常范围为5.275~8.973 V。
入口水温传感器信号有效性判断规则如表1所示。

表1 入口水温传感器信号有效性判断规则表Tab.1 Signal validity judgment rules for of inlet water temperature sensor
2.2 专家系统规则库设计
2.2.1 故障样本数据分析
为了得到不同工况下的各种故障样本,并根据故障样本的数据规律来提取规则,本文对入口温度传感器在不同温度下的各种故障类型进行了现场模拟。 10种故障工况如表2 所示。 不同温度、各种故障工况下的采样电路输出电压值如表3 所示。
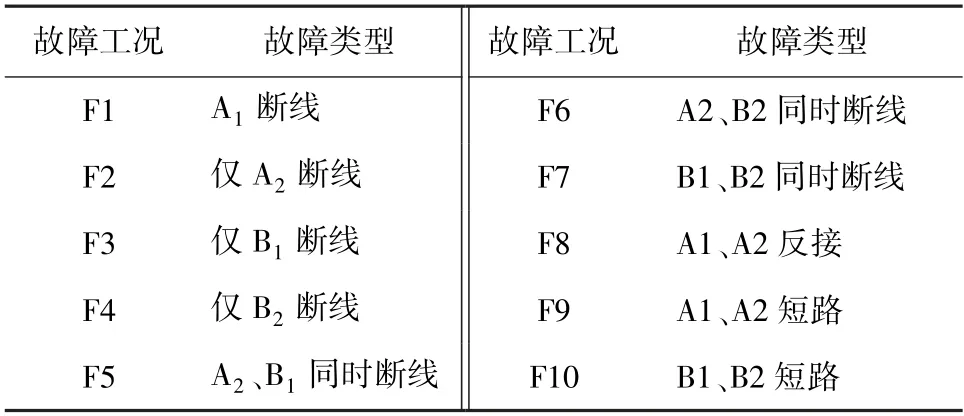
表2 10 种故障工况Tab.2 10 fault conditions

表3 不同温度、各种故障工况下的采样电路输出电压值Tab.3 The voltage outputs of the sampling circuit under fault conditions and different temperatures V
根据表3 的数据,得到不同温度下正常工况与故障工况输出电压值变化曲线,如图3 所示。

图3 不同温度下正常工况与故障工况输出电压值变化曲线Fig.3 Variation curve of voltage outputs under normal and fault conditions at different temperatures
由图3 可以看出,故障工况F2、F4 和F8 时,测量值将偏离正常值且与温度成线性关系。 因此,可通过数据拟合方法得到这三种故障工况下测量值与真实温度间的关系式,从而对这三种故障工况下的真实温度值进行重构。 当传感器处于故障工况F5 或F6 时,其输出测量值恒为-10 V 或+10 V。 利用该特征可识别两种故障工况,但无法重构其真实温度值。 由于故障工况F1、F3、F7、F9 和F10 时的输出电压均为0,所以,只能识别出传感器出现此五种故障,但无法具体定位哪种故障。 对于故障工况F1、F3、F5、F6、F7、F9 和F10,由于无法进行真实温度值的重构,所以需根据灰色预测方法,利用历史正常数据来对其真实温度值进行估计。
2.2.2 故障样本规则库创建及规则提取
正常工况和各种故障工况时输出电压范围值如图4 所示。

图4 正常工况和各种故障工况时输出电压范围值Fig.4 Output voltage range under normal and fault conditions
由图4 可知,正常工况和各种故障工况的输出电压范围值相互独立。 因此,可利用电压范围值与故障类型间的关系建立故障样本规则库,并根据实际测量值重构故障工况F2、F4 和F8 时的真实温度值。
本文建立的基于故障样本的规则库如表4 所示。

表4 基于故障样本的规则库Tab.4 Rule base based on fault samples
2.2.3 故障工况下真实温度值重构
根据表3 所测故障样本数据,采用最小二乘法拟合得到的故障工况F2、F4 和F8 时真实温度值与测量值的重构表达式分别如式(2)、式(3)、式(4)所示,拟合效果分别如图5、图6、图7 所示。
故障工况F2 时,温度真实值重构计算为:
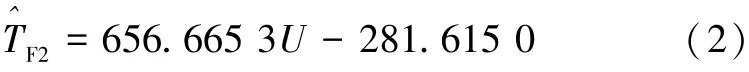
故障工况F4 时,温度真实值重构计算为:

故障工况F8 时,温度真实值重构计算为:

由图5~图7 可以看出,故障工况时的重构温度值与真实温度值几乎重合,拟合效果理想。

图5 故障工况F2 时拟合效果Fig.5 Fitting effect under fault condition F2

图6 故障工况F4 时拟合效果Fig.6 Fitting effect under fault condition F4

图7 故障工况F8 时拟合效果Fig.7 Fitting effect under fault condition F8
2.3 基于灰色预测模型估计传感器真实值
由2.2 节可知,不能基于故障样本数据重构故障工况(除F2、F4、F8 外)时的温度真实值。 但机车运行过程中,会对各传感器温度值进行实时采样和有效性判断。 因此,可利用故障前的正常运行历史数据估计其当前真实温度值。
灰色预测理论由邓聚龙教授提出,利用系统部分数据信息,建立反映系统发展规律的微分数学模型,并通过建立的灰色模型预测系统的发展。 它采用累加生成原理[8],将原始数据生成为一个单调增长的曲线。它增强了原始数据的规律性,弱化了随机性。 本文采用GM(2,1)模型,利用正常历史数据对故障工况下的真实温度值进行估计。
2.3.1 传感器采样数据预处理
下面以现场采样到的牵引变流器柜内的温度数据为例进行算法原理说明。 现场采样的原始数据如图8所示。 原始数据滤波处理如图9 所示。

图8 现场采样的原始数据Fig.8 Orginal data collected on site

图9 原始数据滤波处理Fig.9 Filtering of original data
本文选择入口水温传感器的数据进行建模。 首先,对数据进行滤波处理,得到除噪后的数据波形。 由于温度为缓变的物理量,以100 s 为采样周期,对滤波后的数据进行建模。 滤波后的采样时刻入口水温传感器温度值如表5 所示。

表5 滤波后的采样时刻入口水温传感器温度值Tab.5 Filtered temperature value from inlet water temperature sensor at sampling time
2.3.2 GM(2,1)灰色预测模型建立
综合考虑预测效果和程序运行时间因素,选择6个序列进行建模。 其中:前6 个数据用于建模,后4 个数据用于预测模型的有效性验证。

故而得到方程(5)的通解为:


2.3.3 预测结果分析
基于前述前6 个采样点的正常工况数据,可以建立GM(2,1)模型,并预测其第7 个采样时刻数据。 为了充分利用最新数据,以保证预测模型的有效性,引入预测控制中的“滚动优化”[9-10]思想。 在第8 个采样时刻,若根据前述有效性判断规则判断出第7 个采样数据有效,则舍弃正常历史采样数据,利用最新的6 个正常采样数据进行建模。 基于灰色预测模型GM(2,1)的预测误差如表6 所示。

表6 基于灰色预测模型GM(2,1)的预测误差Tab.6 Prediction errors of grey prediction model GM (2,1)
由表6 可以看出,利用现场正常工况数据,采用GM(2,1)预测模型估计的温度值预测精度高,完全能满足实际应用的需求。
3 结论
本文通过各种故障工况的数据样本和正常历史数据,在分析其数据规律的基础上,结合专家系统和灰色预测模型相关理论,提出了一种温度传感器典型故障的自动识别和容错估计方法。 现场试验表明,该方法原理简单、实现方便、性能优越,具有良好的工程应用价值。
