巧借简图，突破难点

文/广州市荔湾区海北小学 黄利贤

《鸡兔同笼》是人教版小学数学四年级下册第九单元数学广角的内容。本课内容的教学目标是让学生感受古代数学解决问题策略的多样化。在教学的过程中发现学生对于解决此类问题有着浓厚的兴趣，但是有些学生仅仅只知道用“假设法”去解决问题，却不懂其中的道理。因此在解决该问题时，我们考虑借助图文来帮助学生理解和分析《鸡兔同笼》问题，从而让学生很好地掌握解决该问题的方法，进而培养学生的推理能力。

教师在黑板上边画图边解释。

师：假设4个头都是鸡，这样可以算出这时的脚数4×2=8（只），但实际有10只脚，假设比实际少了2只脚，那少了2只脚怎么办？

师：怎么补?是1只脚1只脚分别地补到图里2个头下面是吗？

师：打个比方，如果你拿1只脚补上去，你会发现什么？

生：那补上去就有3只脚，而3只脚既不是鸡也不是兔。

生：那就把2只脚2只脚地补，补上去有4只脚就是兔。

师：没错，我们这时要2只脚2只脚地补，孩子们，你们怎么知道是2只脚2只脚地补？不是1只1只脚地补或者其他方法补？能用算式表示出来吗？

生：4-2=2（只），因为兔4只脚，鸡2只脚，鸡兔相差2只脚，所以要2只脚2只脚的补。

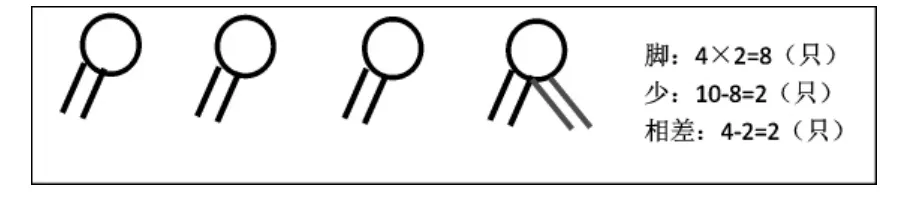
师：那么孩子们思考下，脚是2只脚2只脚地补，可以补几组？

生：1只鸡兔相差2只脚，总共少了2只脚，2÷2=1（组）。

师：也就是求2里面有（ ）个2。

师：刚才补了几组的脚，这时其实就是求出了什么？

生：补了几组的脚，就变成有几只兔。

师：老师把这个方法叫做“补脚法”，把少了的脚补回去，通过画简图分析，理解少的脚应该怎么补，再用转换的思想知道，补了几组其实就是间接求出有几只兔。

通过层层牵引和简图的描述，比较清晰地帮助学生理解多出的脚该如何补，再通过转换的思想，明白补了几组脚就是有几只兔，这就是假设法的难点。学生在这学习过程中假设和转换的思维，这也是凸显了学生学习数学的本质。

在“鸡兔同笼”问题的教学中，我秉承的是教会学生加工信息，适当学习借助一些工具来帮助理解，比如线段图、简图等等，这样有利于帮助学生突破知识的难点，同时也培养了学生的逻辑思维。在练习中，部分学生是直接套入模型“兔的只数=（总脚数－鸡的脚数×总只数）÷（兔的脚数－鸡的脚数）”，课上虽然没总结方法，但部分有预习的学生在听课过程中已总结了做题的模型，感受到数学建模带来的便捷性，也应该鼓励，学习就是多样、开放的。

对于“鸡兔同笼”问题的解决，无论是《孙子算经》中的“半足法”，还是《算法统宗》中的“倍头法”，都具有“只叙述，不讲理”的特点。由此带来的问题是，学习者可以按照操作程序解决问题，但不明白为什么可以这样操作的道理，也就是缺少了“概念性理解”。学习者并不仅仅是去运用数学模型解决问题，更需要去理解形成的过程，理解方法的过程必然枯燥的，可能有些知识很难通过文字或语言来理解，这时运用一种工具——画简图，的确是一个很好的突破口，在教学中如能正确使用，对于突破教学中的难点有很大帮助。