客车订单化生产的动力总成悬置系统方案优化

李智强

（福建船政交通职业学院 汽车学院，福州350007）

车辆动力总成悬置及其构成的振动系统是影响车辆噪声、振动与声振粗糙度（noise vibration harshness，NVH）性能的关键所在，厂家通常花费很大的努力去提升悬置系统的隔振性能以提高乘坐舒适性[1]。客车通常采用订单化的生产方式，客户可以根据需求在正向开发的标准配置基础上，对车辆部分系统和部件的品牌、型号进行选择配置。动力总成一般为可选配置的系统之一，不同品牌、型号的动力总成，其惯性参数和空间尺寸通常不同。动力总成悬置系统需要重新进行匹配设计，使订单配置车辆满足整车NVH性能的要求。悬置系统的正向开发通常需要较长的周期，无法满足订单车辆的要求。订单车辆可以通过选择现有的可用悬置元件，匹配安装位置和角度，以达到较好隔振性能的目标。可选的悬置方案可能不止一个，要对不同的方案分别进行优化分析，得到最优的结果。

目前针对客车订单车辆动力总成悬置系统多方案的优化设计尚未有学者进行详细论述，本文以某型号客车为例，对某订单配置车辆悬置系统的多个可选方案进行优化，最终选择适合该订单车辆的方案。

1 客车动力总成悬置系统建模

1.1 动力总成悬置系统的建模

动力总成悬置系统的设计需要将实际的系统进行必要的简化，得到物理模型，进而建立数学模型以便振动分析和设计[2]。针对客车动力总成悬置系统，建模时做如下假设：（1）动力总成由具有恒定惯性矩阵的不可变形刚体表示；（2）动力总成在其平衡位置附近有较小的位移，支撑动力总成的悬置旋转刚度与平移刚度相比可忽略不计，简化为3根互相正交的弹簧；（3）支撑悬置的车架认为是刚性的；（4）发动机前端驱动带简化为具有一定刚度的弹簧[3-4]。基于上述假设，以本文所研究的商用中型客车为例，动力总成的物理模型可以表示为图1所示。客车动力总成一般为后置后驱，纵向布置，悬置元件一般以气缸中心平面对称布置，四点支撑悬置的定义分别为左前悬置、右前悬置、左后悬置和右后悬置。客车空调压缩机和冷却风扇通常由曲轴通过带传动驱动，皮带弹性力的作用点在曲轴皮带轮中心，在设计计算时，驱动带按照一个在两个方向具有刚度的悬置元件处理。

图1 动力总成悬置系统模型Fig.1 Powertrain mounting system model

定义动力总成坐标系O-XYZ的坐标原点为质心，X轴平行于曲轴中心线指向发动机前端，Z轴与气缸中心线平行，Y轴由右手定则确定。动力总成具有6个自由度，其运动状态可以表示为：x=（x，y，z，φx，φy，φz）T；x，y，z分别为沿坐标轴X、Y、Z方向平动，φx，φy，φz分别绕坐标轴X、Y、Z方向转动。

定义悬置元件坐标系为o-uvw，o悬置元件弹性中心，u、v、w的方向根据悬置的结构来确定。安装在车上时，静态下u与X同向，w与支架的安装平面垂直，向上为正，v向根据右手定则判定。悬置元件在3个弹性主轴的受力可以表示为：

其中，ki=diag（kui，kvi，kwi）为悬置元件的刚度矩阵，kui，kvi，kwi为悬置i在自身坐标系的刚度；Δdi=（Δui，Δvi，Δwi）T为悬置元件的变形向量，Δui，Δvi，Δwi为悬置i在自身坐标系下的变形。

动力总成的振动微分方程，即数学模型可以表示为[5]：

式中，M为质量矩阵，C为阻尼矩阵，K为刚度矩阵，F为悬置受到的外力向量。

1.2 悬置系统传递力计算

由式（1），根据作用力与反作用力的关系，动力总成受到悬置i的力在动力总成坐标系可以表示为：

其中，Ti为坐标O-XYZ到坐标o-uvw的方向余弦矩阵[6]。

类似的，对于悬置的变形有：

Δxi=（Δxi，Δyi，Δzi）T为悬置i在总成坐标系下的位移量。

O-XYZ 3个坐标轴方向的单位矢量分别为i，j，k，悬置i相对于质心的位移可以用矢量表示：

其中，

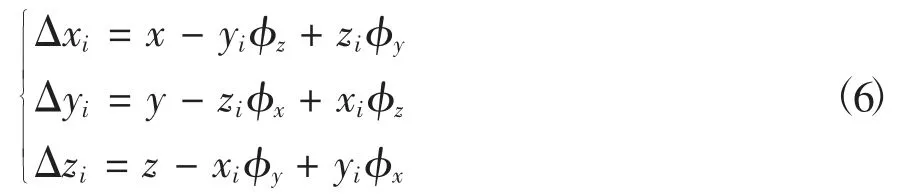
写成矩阵的形式：

式中，xT＝（x，y，z）T，xφ=（φx，φy，φz）T

E为三阶单位矩阵，ri可以表示为：

ri为斜对称矩阵，-ri=。将（7）代入（4）再代入（3）得到：

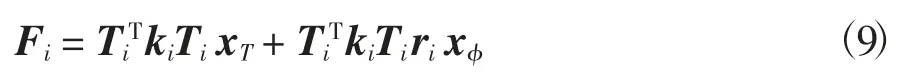
动力总成受到悬置i的力矩作用Mi为：

动力总成受到悬置元件和驱动带的作用力和力矩可以表示为：

2 基于频率和解耦率的方案优化

2.1 订单车辆可选优化方案

商用运营客车的生产方式主要以订单为主，客户可以在公司开发的标准配置车型基础上对某些系统的配置进行选择，动力总成通常有多个可选的配置方案。在订单确定后设计部门需要根据客户的配置方案进行设计开发。在原来类似车型或相同动力总成使用的悬置通常可以用在新的订单配置车型上，这样有多个不同的可供选择的方案。在本文研究的案例中，动力总成前后悬置可供选择的有3个方案，如表1所示。在订单车的设计中，需要对A、B、C 3个方案进行优化设计，并选择其中一个方案。该方案满足在可供设计的空间范围内，有最优的隔振性能。

表1 可供选择的前后悬置方案Tab.1 Available front and rear mounts options

2.2 基于频率和解耦率的方案优化

在动力总成悬置系统设计中，广泛采用系统频率的合理分布和最大限度提升各阶主振动方向的解耦率为目标，对悬置的刚度、安装位置、角度等参数进行匹配[7-8]。根据订单车的特点，刚度参数为多个方案中的其中一个，不作为设计变量，因此设计变量主要考虑悬置的安装位置和角度。设计变量可以表示为：

其中，xf为前悬置在X方向的坐标，yf，zf，xr，yr，zr，以此类推。Ayf和Ayr分别为前后悬置安装角度，即u与Y方向的夹角。

以频率和解耦率为设计目标时，目标函数可以表示为：

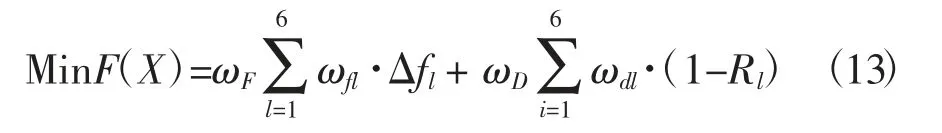
其中，ωF为频率目标的加权系数，ωD为能量解耦率目标的加权系数，ωfl为第l阶主振动方向频率的加权系数，ωdl为第l阶振动方向能量占比的加权系数，l=1～6。Δfl为l阶主振动方向的频率与目标频率的差值，Rl为第l阶主振动方向能量占比。

约束条件主要为悬置元件在设计空间的限制和安装角度、各阶模态频率和解耦率。悬置安装位置的范围可以表示为：

其中，Ayfmin、Ayrmin、Ayfmax、Ayrmax分别为前后悬置安装角度的上限和下限。xfmin和xfmax分别为前悬置在X方向的上限和下限，其余符号的定义以此类推。

各阶频率的约束主要避开路面激励和发动机怠速时最低振动频率，约束频率的范围在4.5到17 Hz。其中Z向频率避开人体敏感区域，约束在10到12 Hz；为避免相邻阶次的振动互相耦合，相邻阶次频率间隔在1 Hz以上[9]。频率约束可以表示为：

其中fl和fl+1分别为l和l+1阶振动的频率，flmin和flmax为l阶频率最小值和最大值。

对于解耦率的约束，要求主要的振动方向Z和绕X方向的解耦率大于80%，其余方向的解耦率大于70%。解耦率的约束可以表示为：

其中，Rlmin为l阶主振动方向解耦率要求的最小值。

动力总成质量为871 kg，绕X，Y，Z方向的转动惯量分别为Ixx=45.1，Iyy=176.7，Izz=160.0，惯性积分别为Ixy=-1.8，Iyz=-0.1，Izx=31.1 kg·m2。分别对本文研究案例中3个方案进行优化，优化前后系统的频率配置和解耦率如图2所示。

由图2（a）可见，优化前方案A在X和Z方向的频率偏低，Y方向和绕X方向的频率过近；方案B在X方向频率偏低；方案C在Y方向、绕Y方向和绕Z方向的频率比较接近。由图2（b）可见，3个方案在解耦率方面比较类似，除Z方向其余方向解耦率偏低，各振动方向耦合严重。

图2 3个方案优化前后的频率和解耦率Fig.2 Frequency and decoupling rate before and after optimization of three solutions

由图2（c）和图2（d）可见，3个方案在优化后，各阶固有频率分布合理，解耦率总体较高，都有较好的振动特性。从频率配置和解耦率的角度，3个方案都是可行的方案，但还要从这3个方案中抉择，选择最终方案，需要对系统进一步分析设计。因此，在订单车的多方案悬置系统优化设计中，基于频率配置和最大化解耦率在方案选择上存在一定的局限性。

3 基于传递力的方案优化

动力总成悬置系统优化主要目的在于保证悬置对动力总成的支撑和可靠性的基础上，减小动力总成振动向车身的传递。由2.2节的内容可知，以频率配置和解耦率为目标对悬置系统进行参数匹配在基于订单生产的客车动力总成悬置系统设计中，存在难以确定最终方案的问题。频率配置和解耦率属于与车辆NVH特性间接关联的特性，各阶模态频率在满足一定范围内，各主振型方向的解耦率有些差异，而总体不相上下的情况下，难以判断系统隔振性能的好坏。因此，进一步选择直接反映悬置隔振性能的传递力为目标进行方案设计。

针对四缸发动机，动力总成振动主要来源于发动机活塞的往复惯性力和曲轴的旋转惯性力[10]。为进一步选择最优系统，综合考虑四缸发动机的特点，以各悬置的垂向传递力、驱动带传递力和绕X方向的扭矩为目标，分别对A、B、C 3个方案进行优化。

设计变量与第2节中基于频率和解耦率的设计相同，约束条件只考虑设计变量的边界条件，不考虑对系统频率和解耦率的约束。设计目标可以表示为：

其中，ωFz为4个悬置在Z方向传递力与驱动皮带传递力之和的加权系数，ωMx为4个悬置和驱动皮带在绕X方向力矩之和的加权系数。优化后3个方案在不同转速下的传递力曲线如图3所示。

由图3可见，3个方案优化后，结果总体差异不大，这表明基于频率配置和解耦率设计的有效性。若优化设计后得到频率布置和解耦率相近的情况下，可以任意选择其中一个方案作为最终方案。基于传递力的方案优化后，方案B优化效果最好，选为最终的设计方案。因此，在多方案的悬置系统优化设计中，以传递力的方法进行优化结果明确。

图3 优化后悬置传递力曲线Fig.3 Transfer force curve of mount after optimization

4 结论

建立了包含驱动带的客车动力总成悬置系统物理模型，推导了悬置及驱动带传递力的计算方法；针对订单生产方式的客车动力总成悬置系统的多方案设计，建立了以频率及解耦率和以传递力为目标的优化设计模型。通过典型案例开展了方案优化工作，表明基于频率和解耦率为目标的方案优化能有效提高系统隔振性能，但是未能确定最终方案。进一步以传递力为目标对多个方案进行优化设计，结果表明以传递力的设计方法能有效减小动力总成振动向车身的传递，同时也便于选出最终的悬置方案。