基于流域形态的山丘区小流域河道宽度计算方法

李 倩

(中水珠江规划勘测设计有限公司，广东 广州 510610)

中国山丘区面积约占国土面积的2/3，自然条件复杂，降雨时段集中，山洪灾害频发，其成灾迅速，冲击破坏力极强，对公共安全和社会经济发展构成巨大威胁。因此，如何预测预报山洪以及减小成灾损失成为国际学术界研究的前沿和热点[1]。2013年中国对29个省、自治区、直辖市下达山洪灾害防治任务，精细化的山洪演进计算工作可为提高山洪灾害监测预警技术的精度提供更科学的理论依据。山丘区的河流断面形态是决定河流输水输沙能力、通畅及稳定程度的重要因素[2-3]，而河道宽度的确定是决定断面形态的关键因素。

目前，国内外围绕河道宽度的计算已进行了大量的模型和理论研究。蒋成伟等[4]、倪飞宇等[5]利用Google Earth影像测量的河宽数据分析了拉萨河流域河宽与地形要素的关系，结果表明河宽与集水面积的相关性最好。何蒙等[6]基于DEM数据提取的河道上游集水面积，模拟了集水面积与河道断面宽度之间的函数关系，并分析了不同流域适用的河宽模型。孙赞盈[7]、张敏等[8]研究了黄河下游河道平衡河宽的计算公式。谢慧民等[9]对台湾西部河流的研究结果表明河宽与集水面积的相关系数均高于其他影响因子。Leopold等[10]、阿尔图宁等[11]、Lee等[12-15]则提出了河宽的理论计算方法。

目前利用河宽模型计算河道宽度需要大量的河道实测地形数据，然而山丘区实测地形资料匮乏，精度较高的河道地形数据也不易获取，实地勘测工作繁重。另外，关于河流宽度的计算公式虽较多，但是对山丘区小流域河宽计算公式的研究计算发现，若计算公式选择不合适，往往会出现较大误差。因此，在简化野外勘测工作的前提下，如何在河道洪水演进中选择更准确的山区河流宽度计算方法，成为了山丘区小流域河道演算的关键问题。

本文对目前常用的河宽计算公式进行归纳总结，并且选择分别基于河流长度和集水面积的2种河道宽度计算公式进行计算分析。同时将河流等级、流域面积及河流长度等特征要素作为河流宽度的影响因素，采用修正后的河流发育系数Kw作为2种河宽公式适用性的选择指标。通过对全国2省市6个山丘区小流域的404个河道断面实测数据与理论计算数据的误差对比分析，提出不同公式的适用条件，并利用山西省北张店流域和湖南省清水站流域的河宽实测数据对结果进行合理性验证。

1 常见河宽计算方法

目前关于河流宽度的研究认为河流宽度与流域下垫面形态以及流量有关，Leopold等[10]提出河宽B与流量Q呈指数关系的计算公式：

B=nQm

(1)

式中 n、m——常数。

阿尔图宁等[11]提出稳定河流宽度与造床流量有关，计算公式如下：

B=αQ0.5/J0.2

(2)

式中Q——造床流量；J——造床流量下的水面比降；α——河床稳定性系数。

还有学者通过统计数据认为天然河流的宽度与集水面积呈指数关系[12-14]：

B=aAc

(3)

式中A——河流某断面以上的集水面积；a、c——常数。

Lee等[15]认为除了以上流域及河流特征外，河流宽度还随河流等级呈线性变化，从而提出河宽与流域面积的关系式，以及河宽与河流长度的关系式，分别为式(4)、(5)：

(4)

(5)

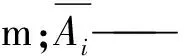
目前关于河流宽度的计算公式主要认为河流宽度与流量、流域面积、流域特征及河流形态有关，由于流量的确定受水文数据限制，使用很不方便。在确保计算精度的前提下，为了简化野外勘测调查工作，本文选择了能够反映流域特征和河网形态的河宽计算式(4)、(5)，采用修正后的河流发育系数作为选择指标进行河宽计算公式的优选，从而构建一套适用性更好的河流宽度计算方法。

2 山丘区小流域河流宽度计算方法

2.1 河流等级划分

河流等级划分采用Strahler分级方法，根据实际山丘区小流域的等级划分情况可知，河流等级一般最高为3～4级，根据式(4)、(5)，流域内的河流宽度可由流域出口处河流宽度及流域特征数据计算得到，从而需野外测量的数据只有流域出口断面的河宽，见图1。

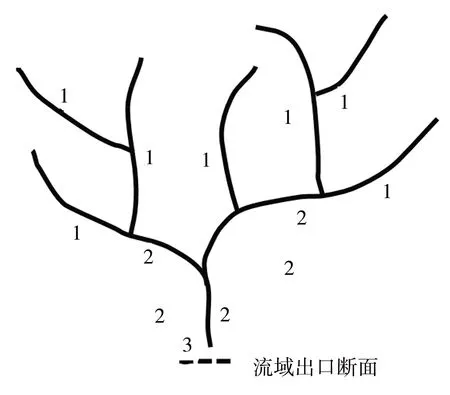
图1 Strahler法划分河流等级

式(4)、(5)分别基于河流等级的集水面积和河流长度为计算依据，但是两公式计算结果有时相差较大，在不同流域选择哪个公式来推求河流宽度，成为了山洪演进计算的关键。由于不同的流域水系形态对河道流量及洪水水情有不同影响，从而影响河道几何形态特征。此外，流域水系形态还与式(4)、(5)中涉及的河流等级有关，因此选取与流域水系形态相关的系数作为河宽计算公式的选择依据。

2.2 河宽公式选择指标

一般采用流域形状系数来描述流域形态，流域形状系数Ke是流域分水线的实际长度与流域同面积圆的周长之比。Ke值接近于1时，流域的形状接近于圆形;Ke值越大，流域形状越狭长，见图2。

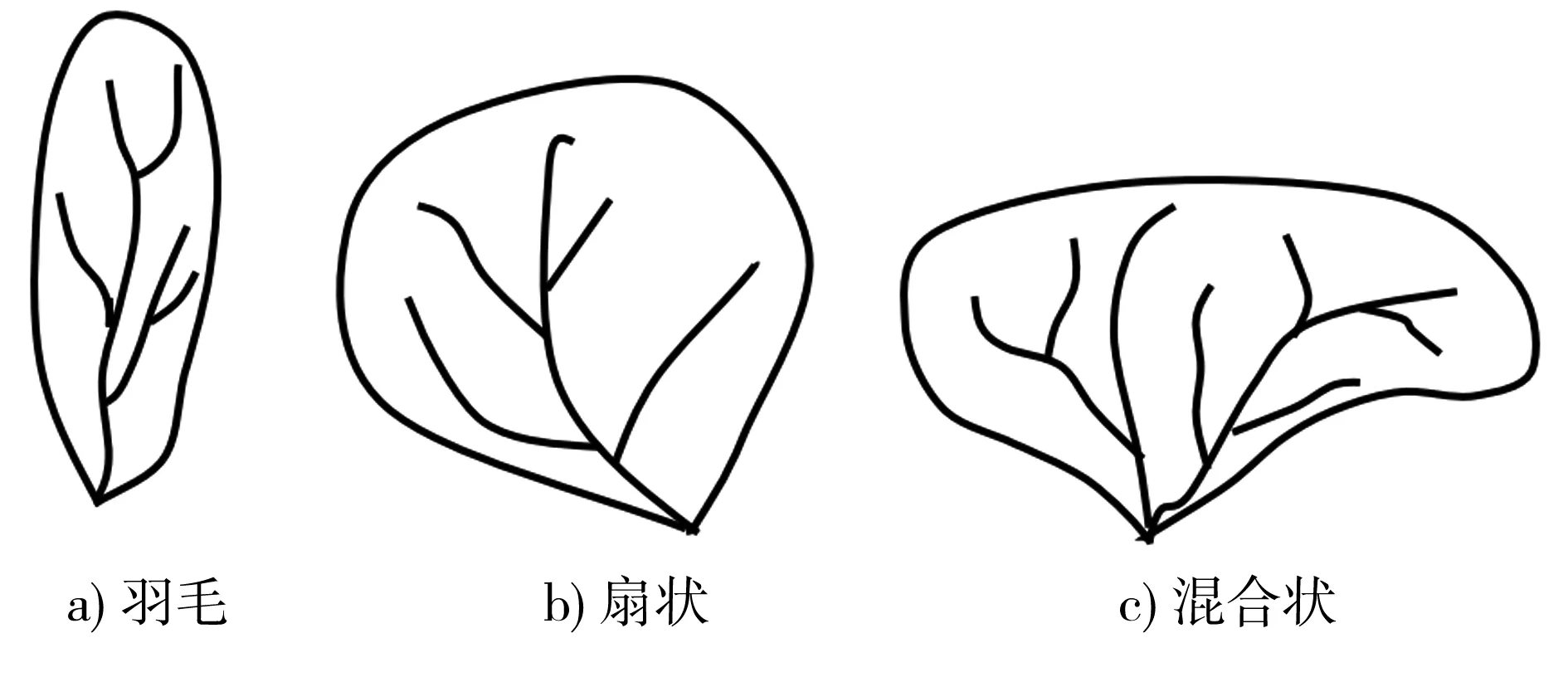
图2 流域水系形状分类

但对于图2中的狭长羽毛状水系和扁宽的混合状水系而言，2流域水系均不接近圆形，当流域面积相同时，2水系的分水线长度存在大小接近的可能，从而流域形状系数Ke值大小接近，因此Ke不能准确地分辨这两种流域及河网的形态特征。

针对该问题，选用河流发育系数来描述流域河网特征。河流发育系数是指支流总长度与干流长度之比，是描述河网各级河流构成的系数。为了进一步反映流域各级河流长度对全流域水系形状的影响，河流发育系数Kw修正为某一级支流总长度与流域河网总长度之比，河宽公式的选择指标采用修正后的Kw，其计算方法为式(6):

(6)

式中Kw——河流发育系数；Lw——第w级河流长度，m；w——河流等级，w=1、2、3……n；L——河网总长度，m。

2.3 河宽公式选择

本文采用国家山洪灾害调查评价项目中福建、北京2省市6个山区小流域的河网及404个实测河道断面数据进行分析，有实测资料的流域出口处河流等级最高，一般在2～4级；山区河流的等级较小，一般在1～3级，且缺乏实测断面资料，其河流宽度根据流域出口实测河宽分别由式(4)、(5)计算，结果见表1。

由表1可知，在河流位于集水面积小于150 km2的流域时，采用式(4)、(5)算法得到的河宽相对误差均在20%以内，平均相对误差分别为4.6%和6.8%，2种公式计算结果均接近实测宽度。对流域面积大于150 km2的小流域，若仅用式(4)、(5)中的一个公式计算，相对误差较大。其中，门头沟流域计算误差超过50%，乌墩流域高达270%。若以河流发育系数作为公式选择指标，①当河流发育系数Kw<0.70时(乌墩及房山流域)采用基于集水面积的河宽公式(4)，得到的结果精度较高，相对误差均在12%以内，平均相对误差为6.1%；②当河流发育系数Kw≥0.70时(门头沟流域)，采用基于河长的河宽计算公式(5)，计算河宽结果更接近实测河流宽度，相对误差均在5%以内，平均相对误差为3.2%。从而可得到河宽公式的适用性标准见图3。

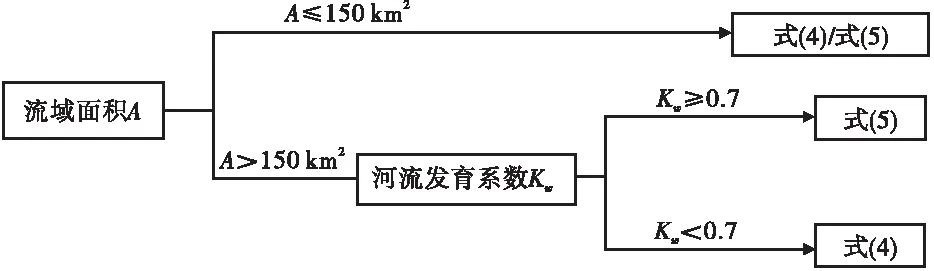
图3 河宽计算公式选择指标及流程

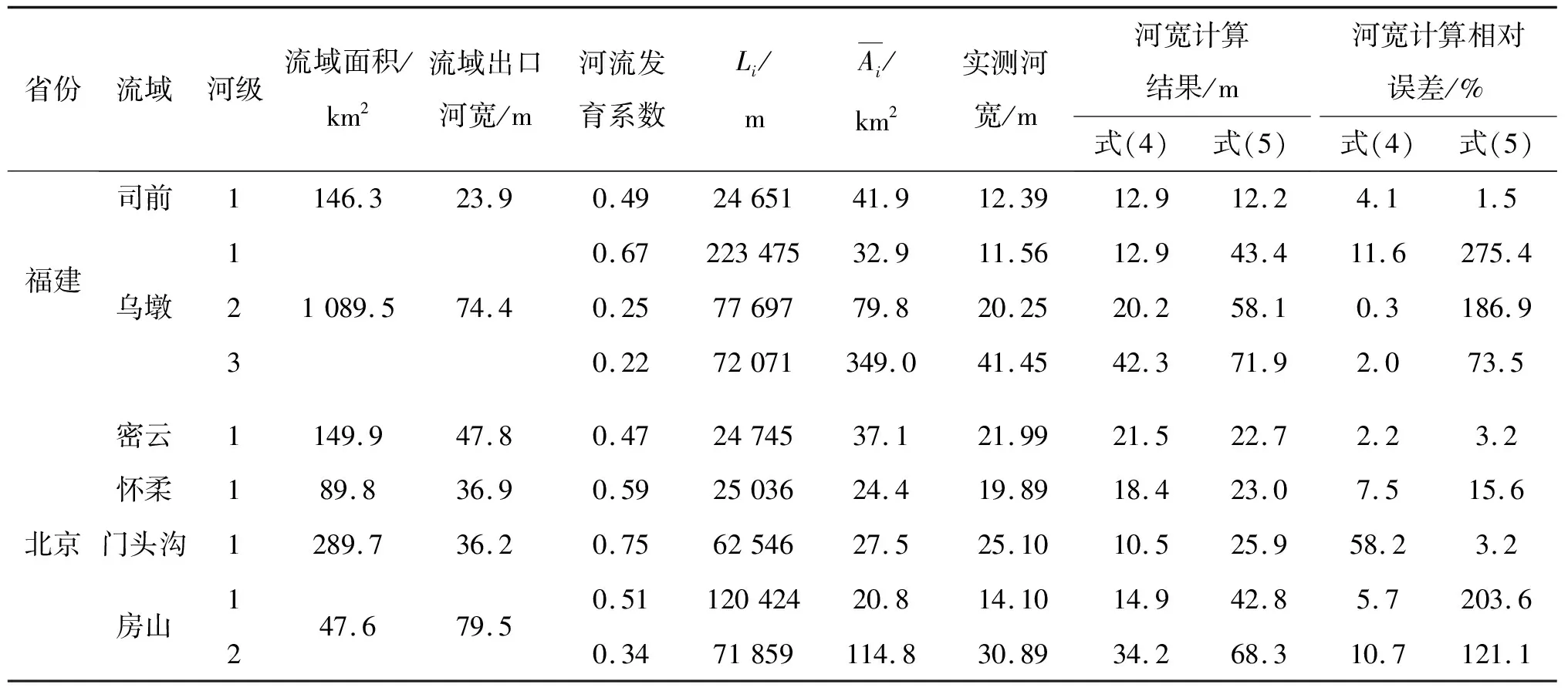
表1 山区流域河流宽度计算

若单一无差别地全部采用式(4)、(5)计算以上6个流域的河宽，计算结果的平均相对误差分别为11.4%或98.2%；若采用图3所示的河宽公式选择标准及流程得到的计算结果与实测河宽比较，其平均相对误差为5.3%，计算精度得到大幅提高。

3 应用与验证

为了验证本文提出的河宽计算方法的合理性，选取有实测数据的山西省北张店流域和湖南省清水站流域进行验证。

3.1 流域概况

北张店流域位于山西省屯留县，流域面积为271 km2，矢量数据及河道实测数据来自全国山洪灾害调查评价工作；清水站流域位于湖南省长沙市浏阳县，流域面积34.2 km2，矢量数据来自无人机探测数据，流域示意见图4。

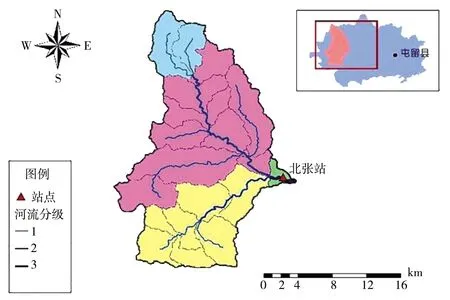
a)北张店流域

3.2 计算结果

清水站流域面积小于150 km2，根据河宽公式计算流程，采用2种公式均可计算，北张店流域面积大于150 km2，根据河宽发育系数Kw选择计算公式，计算结果与河道的实测宽度进行对比验证，见表2。

由表2可知如下结果。①清水站流域面积小于150 km2，采用2种公式计算的河宽结果比较接近，相差不超过0.6 m；其中只有1级河流的计算结果相对误差较大，原因是该流域面积较小，1级河流的河宽较小，因此相对误差较大达到43.5%，而绝对误差为0.83 m；2级河流计算河宽的绝对误差均不超过0.3 m，平均相对误差不超过6%。②北张店流域面积大于150 km2，河流发育系数Kw<0.7,采用式(4)计算河流宽度，相对误差在6%～12%，式(5)的计算相对误差均在23%～48%；因此，选择式(4)计算结果明显精度更高，同时也验证了河宽公式选择指标及流程的可靠性。

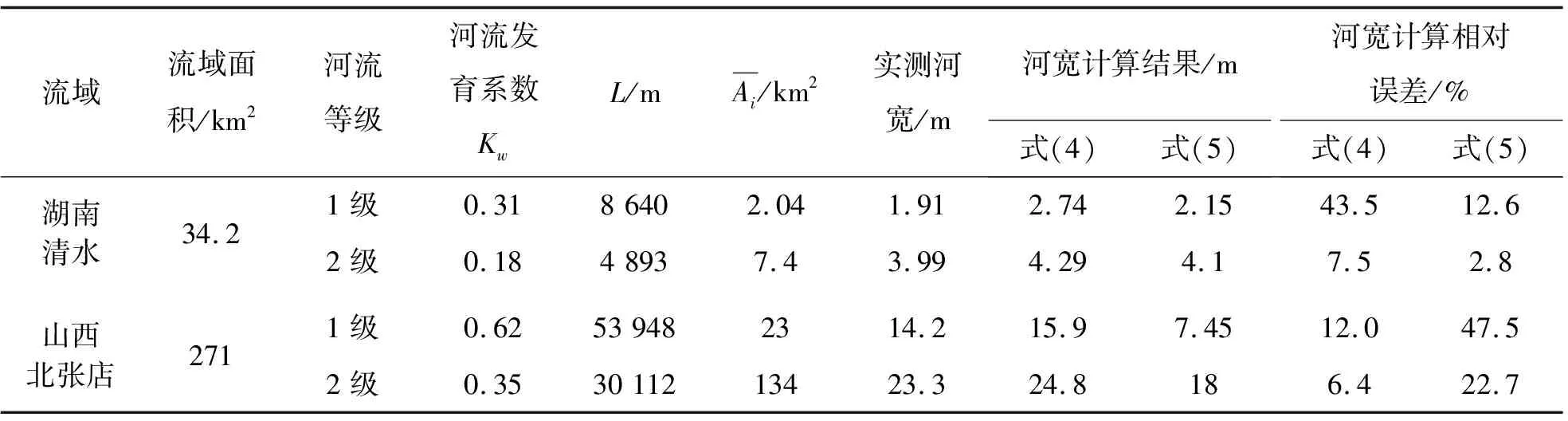
表2 验证流域河流宽度计算

4 结论

基于对多个山丘区小流域河宽实测数据与计算数据的综合分析以及对计算方法合理性和精度的验证，提出一套山丘区流域河流宽度的计算方法，结论如下。

a)流域面积小于150 km2时，选择2种计算公式均可。

b)流域面积不小于150 km2时，根据河宽发育系数Kw的大小判别。若河宽发育系数Kw<0.7时,采用基于集水面积的河宽公式(4)计算河流宽度；若河宽发育系数Kw≥0.7时,采用基于河长的河宽公式(5)计算河流宽度。

c)此方法的优势在于一方面仅需测量流域出口处的河流宽度，从而减少了缺资料流域野外勘测的工作量；另一方面按此方法得到的计算结果误差较小，保证了山丘区流域河流宽度的计算精度。

d)该研究结果可为水文资料匮乏的山丘区流域提供了一套基于流域水系形态获取河流宽度的计算方法，并为山洪灾害防治方案制定提供技术支持。但由于掌握的资料有限，本文提出的河宽计算方法需在进一步的实际应用中予以完善。