基于混沌系统的扩频通信多源异构数据加密算法

张人上，邱久睿

（1.山西财经大学信息学院，太原 030006；2.山西财经大学经贸外语学院，太原 030006）

0 引言

扩频通信是一种信息传输方式，信号占据的频带宽度远远大于所传信息需要的最小带宽。频带扩展是利用独立码序列，通过调制与编码方法实现的，与所传信息数据没有联系［1］。接收端利用相同码同步接收、解扩并恢复所传信息数据。扩频通信具备重复使用频率高、抗干扰性强、误码率低、隐蔽性好、抗多径干扰、精确定时与测距、安装简便、易于维护等优势，被包括军事通信、移动通信、卫星通信、测距定位等在内的多个领域应用，具备极好的应用前景［2］。

由于扩频通信方式具备共享、开放的特征，为传递数据安全性带来了威胁。近几年，通信病毒种类不断增加，信息泄露、私密文件窃取案件频频发生，为大众带来了巨大的经济损失。扩频通信应用过程中会产生大量的多源异构数据，为了保障扩频通信的安全性，加密处理多源异构数据势在必行［3］。

扩频通信使用范围的扩展，导致多源异构数据体量呈指数级别增加，传统加密算法力不从心，加解密速度低下，影响扩频通信的应用效果，为此提出基于混沌系统的扩频通信多源异构数据加密算法研究。混沌系统指的是在一个确定性系统中，存在着随机不规则运动，其行为表现为不可预测、不可重复、不可确定，即为混沌现象。旨在通过应用混沌系统提升加密算法的性能［4］。

1 扩频通信多源异构数据加密算法

1.1 多源异构数据混沌映射

扩频通信多源异构数据表面上毫无规则、类似随机，实际上存在一定的规则［5］。混沌映射具有多种方法，例如Logistic、Henon、Tent 等，通过借鉴已有研究文献发展，Logistic 混沌映射具备较强的混沌特性、输出过程复杂、控制参数集大等优势，故此研究利用Logistic 混沌映射多源异构数据，具体映射过程如下所示［6］。

假设时刻t 的扩频通信多源异构数据为xn，第t+1 时刻，扩频通信多源异构数据为xn+1，两个时刻数据的关系可以用函数关系表述，函数关系为

利用Logistic 混沌映射转换式（1），得到多源异构数据映射关系表示为

综上，利用混沌系统映射多源异构数据，为数据加密做准备。

1.2 多源异构数据混沌序列生成

以上述得到的多源异构数据混沌映射结果为基础，生成多源异构数据混沌序列，简化数据加密程序［8］。

通过对比研究成果发现，二值序列与扩频通信多源异构数据加密更为契合，故式（4）即为生成的多源异构数据混沌序列［10］。

1.3 多源异构数据时序控制

多源异构数据时序控制是指控制迭代运算结果的输出，并为下述子密钥的产生提供选择信号［11］。

时序控制由Merlay 状态机实现，其状态转移情况如图1 所示。

图1 Merlay 状态机状态转移图

如图1 所示，WaitKey 状态是指等待子密钥；key_ready=1 指子密钥到达，进入下一个状态；Wait-Data 状态指等待多源异构数据状态；1data=1 指多源异构数据到达，进入RepeatRound 状态；RepeatRound ＜15 指的是16 次迭代过程；当RepeatRound=15 时，进入FinalRound 状态；FinalRound状态结束后，即输出子密钥有效信号［12］。

单轮迭代运算流程如图2 所示。

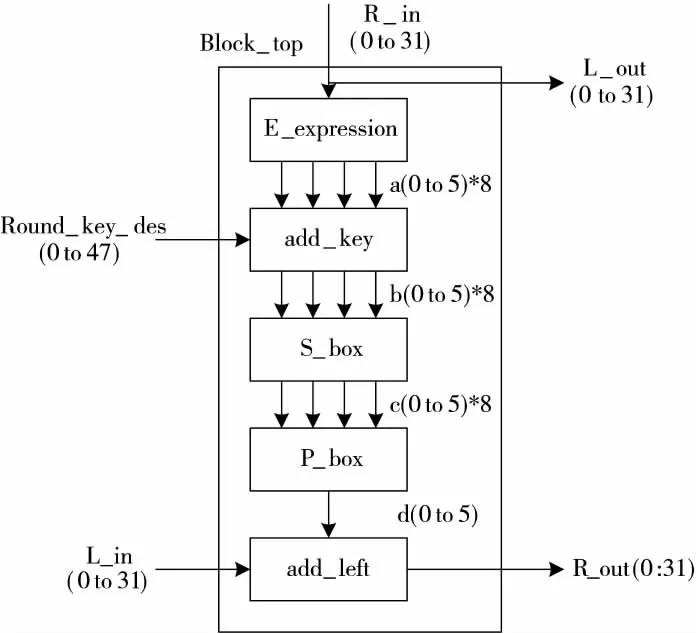
图2 单轮迭代运算流程图

如图2 所示，迭代运算中包含着一系列运算，例如E-expression 选择扩展运算、add_key 异或加密运算、S_box 压缩运算、P_box 置换运算与add_left 异或运算［13］。

通过上述流程得到迭代运算结果，为子密钥的产生提供信号支撑。

1.4 子密钥产生

传统数据加密算法原始密钥输入是固定的，采用相同原始密钥生成每轮子密钥对数据进行加密或者解密，存在着加密与解密密钥同步问题［14］。利用Logistic 混沌映射生成的二值序列产生每轮子密钥的手段，很好地解决了上述问题，具体子密钥产生过程如下所示。

截取二进制序列流的64 bit 与明文的头64 bit序列经过异或转换即为原始密钥，可以使数据加密与解密过程的原始密钥既是同步的，又是可变化的。

提出算法每轮子密钥迭代运算是通过输入不同参数，以及轮函数来实现每轮数据加密的混沌特性。而轮函数是一个非线性函数，具有较好的加密效果，保证了提出算法的安全性［15］。

轮函数是对输入的多源异构数据进行替换，数量为8 个，以第1 个轮函数为例，其余替换过程与第1 个轮函数相同。轮函数置换表结构如表1所示。通过上述轮函数的应用，得到了多源异构数据的子密钥，极大的加快了提出算法的执行速度。

表1 轮函数置换表结构

1.5 多源异构数据加密运算

将上述得到的多源异构数据与子密钥进行正向或者反向异或，具体操作如下所示。

正反向取模得到的结果即为加密过后的扩频通信多源异构数据，实现了扩频通信多源异构数据的加密，为扩频通信的应用安全性提供更加高效的保障。

2 加密算法性能测试

扩频通信多源异构数据加密算法的安全性由密钥敏感性、抗统计特性、加密效率指标决定。扩频通信多源异构数据包含图像、音频等多种类型，为了测试提出算法的性能，分别在图像与音频数据类型下进行测试，具体测试过程如下所示。

2.1 密钥敏感性分析

常规情况下，对于性能良好的算法来说，即使密钥发生极其微小的变化，便无法得到正确的原始数据信息。为此，密钥敏感性越高，则算法性能越好。

在图像数据类型仿真测试中，选取同一初始条件，设置作为加密密钥，以差值为+10-13密钥作为对比值，得到解密图像如图3 所示。

图3 图像数据解密图像

在音频数据类型仿真测试中，选取同一初始条件，设置x 作为加密密钥，以差值为+10-13密钥作为对比值，得到解密图像如图4 所示。

图4 音频数据解密图像

如图3 与图4 所示，设置密钥差值为+10-13，在密钥为x+10-13情况下，无法解密出正确数据，表明提出算法密钥敏感性极高。

2.2 抗统计特性分析

2.2.1 图像数据类型测试

图像数据抗统计特性主要由加密前、后直方图以及相关性决定。具体测试过程如下：

选取规格为256×256 的图像作为测试对象，利用MATLAB 仿真得到加密前、后的图像直方图，并进行对比，通过图像直方图的分布情况判定算法抗统计攻击的有效性。常规情况下，若直方图分布均匀、平整，则判定提出算法具备良好的抗统计特性，反之，则提出算法抗统计特性较差。

通过测试得到图像加密前、后的直方图情况如图5 所示。

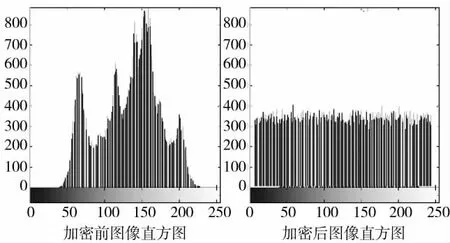
图5 图像加密前、后直方图

如图5 所示，加密后图像直方图分布均匀，并很平整。

加密前、后图像具有较大的相关性，据研究发现，相关性越小，越有利于抵抗统计攻击。因此，性能好的算法可以很好地降低相关性数值，保障图像元素之间具备较好的独立性。

选取3 幅图像作为测试对象，并简称其为图像1、图像2 与图像3。设定Logistic 混沌映射初始值x0为0.786，分别在水平、垂直、对角3 个方向选取加密前、后图像的2 000 对像素，计算加密前、后图像相关系数，公式表示为

以测试对象为基础，通过式（9）计算加密前、后图像的相关系数，得到加密前、后图像相关系数对比情况如下页表2 所示。

表2 相关系数对比表

如表2 所示，加密后图像相关系数急剧下降，并接近为0。

通过图5 与表2 测试结果显示，在图像数据类型下，提出算法具备较好的抗统计特性。

2.2.2 音频数据类型测试

音频数据抗统计特性由加密前、后音频频谱图以及相邻点相关性决定。

测试对象为音频test2.wav，通过MATLAB 仿真得到加密前、后音频频谱图如图6 所示。

图6 加密前、后音频频谱图

通过测试得到加密前、后音频相邻点相关性如图7 所示。

图7 加密前、后音频相邻点相关性图

如图6 所示，加密前音频频谱数值分布不均匀，容易泄露数据，而加密后音频频谱数值分布均匀，可以确保数据安全。如图7 所示，加密后音频元素分布无规律，并布满整个空间，几乎没有关联，相关性较低。测试结果表明，基于音频数据类型，本研究提出的算法具备较好的抗统计特性。

2.3 加密效率分析

在测试环境（i3 处理器、4GB 内存、500 G 硬盘）下，选取View、Sailboat、Bridge、Goldhill、Boats、Pepper、Couple、Cameraman、Lena 9 张图像作为测试对象，通过MATLAB 仿真，计算提出算法的加密时间，得到数据如表3 所示。

表3 加密时间数据表

常规情况下，数据加密最高限值为21.356 s。由表3 数据显示，提出算法的加密时间范围为16.451 s～18.630 s，均低于最高限值。

3 结论

本文提出基于混沌系统的扩频通信多源异构数据加密算法，解决因多源异构数据体量呈指数级别增加，数据时序混乱的问题，生成多源异构数据混沌序列，完成实现扩频通信多源异构数据的加密。上述测试数据显示：在图像与音频两种数据类型下，提出算法的密钥敏感性与抗统计特性较好；以图像为测试对象，得到加密时间范围为16.451 s～18.630 s，均低于最高限值21.356 s，说明提出算法加密效率较高。测试结果充分表明提出算法具备较好的性能，可以大力推广应用。