基于双声道的低压超声气体流量计数据融合方法

赵伟国,卜勤超,姚海滨,章圣意,章 涛

(1.中国计量大学 计量测试工程学院,浙江 杭州 310018;2.浙江苍南仪表集团股份有限公司,浙江 苍南 325800)

1 引 言

时差法气体超声流量计通过测量超声束在流体介质传播的顺逆流飞行时间差来计算通过管路截面的平均流速[1],有无可动部件、压损低、准确度高、量程比宽等优点,已应用于燃气、医疗、芯片制造等多个领域。在高压气体测量中,采用多声道测量不同平面的流速,通过权重系数法、神经网络法等进行多声道时差数据融合,降低管路内流场分布对流量测量的影响[2～5，15]。对于低压气体的测量,由于受管道几何尺寸的限制,一般采用双声道的流量测量方法。然而在低压气体测量中,由于超声波在气体介质中传播的衰减较大、信噪比低、回波信号易受流场干扰,导致声道的时差数据发生异常或错误,从而使传统的固定权重系数融合算法产生较大的误差。

针对以上问题,本文提出了一种基于双声道的超声波流量计数据融合方法,首先对单一声道的时差数据进行粗大误差剔除和流量计算,再通过时差数据进行预估处理获得流量状态和传感器故障信息,然后根据预估状态采用递推型卡尔曼滤波算法计算出管道内气体的流量。

2 超声气体流量计数据融合方案

双声道气体超声流量计采用Z法(直射式)测量的声道布置方式,其中换能器A和B为一个声道,换能器C和D为另一个声道,4个换能器位于一个平面,管路内径为50 mm,测量管路图如图1所示。

图1 双声道气体流量计测量管路Fig.1 Measuring pipe of double-channel ultrasonic flowmeter

采用的数据融合方法如图2所示,首先对单个声道的时差数据进行粗大误差剔除,再经过数据处理和分段线性拟合进行流量计算,最后通过卡尔曼算法进行双声道数据融合实现流量状态判定与故障诊断。

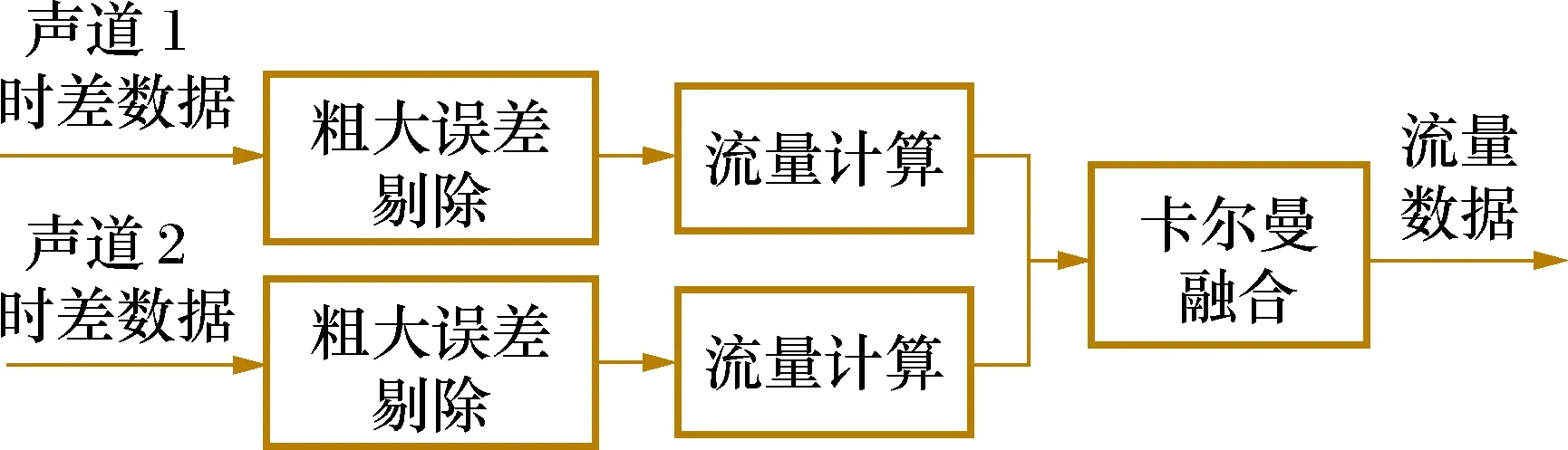
图2 双声道气体流量计数据融合流程图Fig.2 Data fusion chart of double-channel ultrasonic flowmeter

3 时差数据粗大误差剔除

由于各个声道每1 s可测得50个时差数据,因此时差数据可采用肖维勒准则或格拉布斯准则进行粗大误差剔除。为确定粗大误差的剔除方法,对流量计测得的时差数据进行数值仿真研究。在某一流量点下,将采集得到某一声道1 s内的时差数据分别用格拉布斯准则和肖维勒准则进行粗大误差判断,识别结果如图3所示。

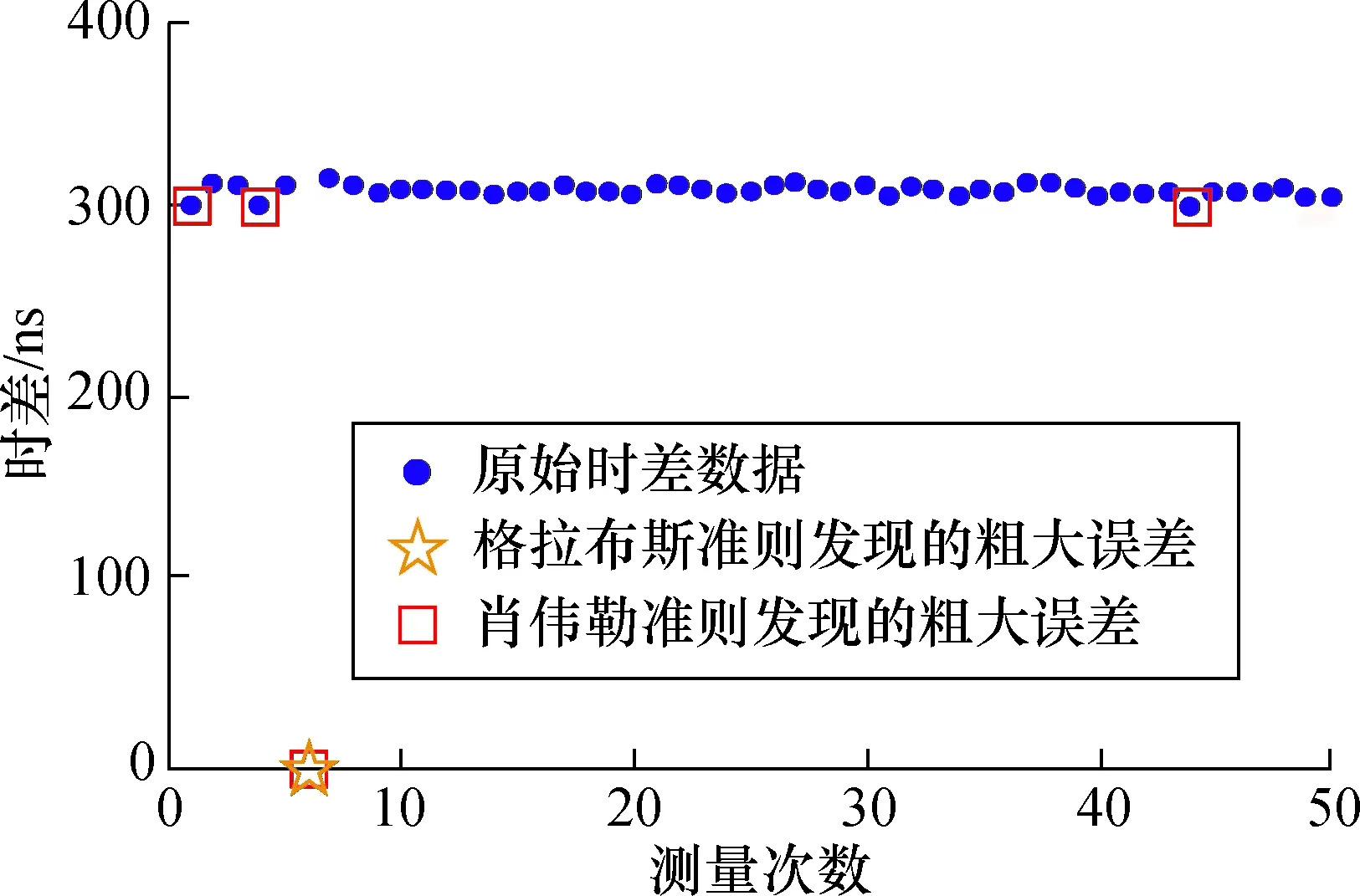
图3 粗大误差判断方法数值仿真Fig.3 Numerical simulation of gross error judgment method

根据数值计算结果可以发现,2种准则都将第6个数据识别为粗大误差,但是通过肖维勒准则还识别出另外3个时差数据为“粗大误差”,但从图3可以判别出这3个“粗大误差”与其它正常数据并没有明显的差异,无法认定其为粗大误差。因此,格拉布斯准则更适合于粗大误差剔除的判断标准[6]。

4 流量计算

流量计算是对剔除粗大误差的时差数据进行数据处理后,再进行分段线性拟合计算出流量修正值。常见的数据处理方法有算术平均法,中值滤波法和分批估计法[7,8]。这3种方法都可以减少系统随机误差,为了比较这3种数据处理方法在实际流量测量过程中提高测量精度的有效性,根据不同数据处理方法得到的流量值与实际流量的均方误差作为评价数据处理方法优劣的指标,具体的结果表1所示。

表1 不同数据处理方法仿真结果(均方误差)比较Tab.1 Comparison of simulation results (mean square error)of different data processing methods m3/h

由表1可知在流量较小时利用算术平均法处理后的数据均方误差较小,而在流量较大时中值滤波法处理后的数据均方误差较小。而分批估计处理方法相对于其它2种方法计算较为复杂,但测量效果却没有明显优于其它2种方法,因此选用算术平均法与中值滤波结合的数据处理方法,即将数据分别进行算数平均法和中值滤波法处理,然后取平均作为每一声道的时差数据。

在多个不同标准流量情况下,分别通过测量得到的每个声道时差计算出流量,然后分别计算每个流量点下,测量流量与实际流量的相对误差并绘制误差曲线,具体见图4所示。因此,流量可以通过分段线性拟合进行修正,从而得到每个声道的流量。

图4 计算流量与实际流量的相对误差曲线图Fig.4 Relative error curve of calculation flow and actual flow

5 基于卡尔曼滤波的数据融合方法

5.1 多传感器卡尔曼融合

多传感器卡尔曼融合方法按照融合结构可以分为集中式融合和分布式融合[9]。分布式融合是对多个传感器在某一时刻得到的测量向量的,先分别进行单传感器卡尔曼滤波得到局部估计,然后对局部估计结果进行融合,已在多声道超声流量测量中应用[10]。双声道的卡尔曼融合方法流程简图见图5所示。

图5 卡尔曼分布式融合方法流程图Fig.5 Flow chart of kalman distributed fusion method

在双声道超声波流量计中,将2个声道测量计算的流量进行融合,则系统的状态方程和观测方程[11,12]为:

(1)

式中:x(t)为t时刻的系统状态,即为管道内实际流量;q(t)系统噪声,其协方差为Q;zi(t)为观测值,即流量计两声道各自的测量值;ri(t)为测量噪声,其协方差为Ri,i=1,2。

因此可由当前t时刻系统状态x(t|t)分别得到下一时刻两声道的先验估计值xi(t+1|t)为:

xi(t+1|t)=x(t|t)

(2)

则有误差协方差Pi(t+1|t)为:

Pi(t+1|t)=Pi(t|t)+Q

(3)

根据式(2)和式(3)可迭代求得卡尔曼增益Ki(t+1),后验估计值xi(t+1|t+1)并更新误差协方差Pi(t+1|t+1),其递推公式分别为:

Ki(t+1)=Pi(t+1|t)·[Pi(t+1|t)+Ri]-1

(4)

xi(t+1|t+1)=xi(t+1|t)+Ki(t+1)·

[zi(t+1)-xi(t+1|t)]

(5)

Pi(t+1|t+1)=[1-Ki(t+1)]·Pi(t+1|t)

(6)

由式(4)～式(6)所示迭代公式可得互协方差P12(t+1|t+1)|为:

P12(t+1|t+1)=[1-K1(t+1)]·

[1-K2(t+1)]·[P12(t|t)+Q]

(7)

根据式(5)和式(6)可得x1(t+1|t+1)、x2(t+1|t+1)和对应的误差协方差P1(t+1|t+1)、P2(t+1|t+1)可融合得到系统融合状态值x(t+1|t+1)为:

x(t+1|t+1)=

(8)

式中h1,h2,h3,h4分别为:

(9)

在实际双声道气体流量计的应用中2个声道互不相关,因此互协方差P12(t+1|t+1)=0,由式(8)可得系统融合状态值:

(10)

由式(1)～ 式(10)可知,基于卡尔曼融合方法实现状态预测、预测修正、方差更新及状态融合的过程可在传感器正常情况下实现数据融合[13]。但当传感器发生故障时,该方法无法识别故障传感器并剔除异常传感器数据,会影响系统正常工作。

5.2 改进的卡尔曼分布式融合算法

卡尔曼分布式融合算法是在得到各个传感器局部最优估计的基础上的优化融合,其融合可靠性较高,但是卡尔曼分布融合方法并没有对传感器的可信度进行评估,无法识别故障的传感器并剔除其数据。因此,提出了一种改进的卡尔曼分布式融合算法,根据2个声道的时差数据进行流量状态估计和故障诊断,并进行卡尔曼数据融合。

首先,对2个声道1 s内的时差测量数据进行双总体U检验。通过双总体U检验可检验2个样本平均值所代表的总体差异是否显著,适用于检验样本量较大的独立样本平均值差异显著性,其检验统计量为:

(11)

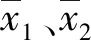
系统中声道1和声道2分别测量得到时差数据ΔT1、ΔT2,反映管道内的流量Q。将当前2个声道的时差数据进行双总体U检验,得到U12(t)以判断2个声道的差异是否显著。为了判断各个声道连续2 s的流量测量差异性是否显著,则通过计算统计量U11(t)、U22(t)获得。最后,根据U11(t)、U22(t)和U12(t)各个统计量得到当前流量计的测量状态。具体判断准则见表2所示。

表2中:ε为显著性水平α=0.01时双总体U检验的临界值;b1、b2分别为两声道的卡尔曼融合系数。

表2 双声道气体超声流量计测量状态判定表Tab.2 Measuring status determination table of double-channel ultrasonic flowmeter

通过表2判断超声波流量计状态,可以识别故障声道和流量状态,通过剔除故障声道的测量数据保证测量的准确性,则卡尔曼分布式融合式为:

(12)

6 数据融合方法实验验证

将测量管路安装在音速喷嘴流量标准装置上进行实验研究。首先,在流量160 m3/h下,将采集的2个声道的时差数据进行粗大误差剔除、分段线性拟合,得到双声道气体超声波流量计的流量测量值,利用MATLAB分别对改进的卡尔曼分布式融合算法和双声道加权融合算法进行双声道数据融合,结果见图6所示。

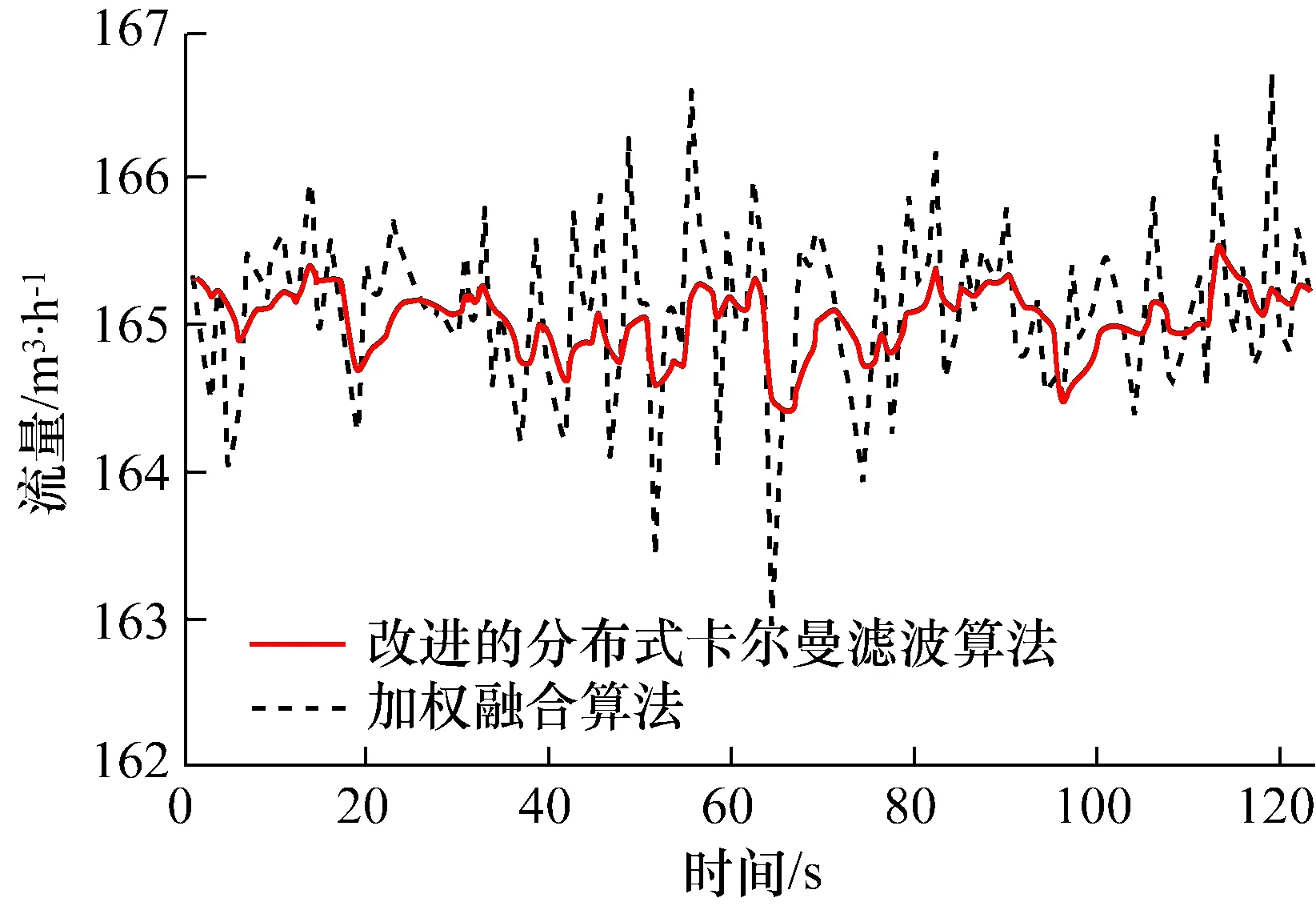
图6 数据融合算法效果对比图Fig.6 Data fusion method effect comparison diagram

从图6可以发现,采用改进的卡尔曼分布式融合算法对双声道流量数据进行数据融合的曲线比加权融合算法进行数据融合的曲线更加光滑,波动更小。考虑到流量实验是在音速喷嘴标准装置上进行的,实际流量是平稳的,因此改进的卡尔曼分布式融合算法具有较好的准确性。

为了验证某一声道故障数据的融合算法效果,在流量160 m3/h下进行120 s的数据采集,当60 s左右时,将声道2的传感器C挡住,使声道2的时差数据发生错误(时差设为0)。然后对不同声道的数据分别采用加权算法、改进的卡尔曼融合算法进行处理,结果如图7所示。

图7 融合算法故障识别图Fig.7 Fault identification diagram of fusion method

由图7可知当声道2在60 s左右产生故障,声道2流量测量数据降为0,声道1数据正常。采用改进的卡尔曼分布式融合算法可识别故障声道,并剔除对应的故障数据,根据声道1的流量测量数据进行滤波处理,保证流量计正常工作。而加权算法由于没有识别故障,使测量结果产生较大的偏差。

为验证改进的卡尔曼分布式融合算法的动态特性,流量从160 m3/h急速切换为20 m3/h,将采集的2个声道数据分别进行改进的卡尔曼分布式融合算法和加权融合算法计算,数据结果如图8所示。由图8可知当流量由160 m3/h切换为20 m3/h时,使用加权融合算法和改进的卡尔曼分布式融合算法得到的流量都随之出现变化,都具有良好的动态性能。

图8 数据融合算法动态性能图Fig.8 Dynamic performance diagram of data fusion method

最后,根据JJG 1030—2007超声流量计检定规程[14],对设计的双声道气体超声流量计样机进行流量性能测试,流量点应分别为:Qmin、Qt、0.25Qmax、0.4Qmax、0.7Qmax和Q,每个流量点检定次数不少于3次。

为了对比加权融合算法与改进的卡尔曼分布式融合算法(表中简称改进的卡尔曼算法)在实际流量测量过程中的测量精度与准确性,对2种方法进行流量对比实验,结果如表3所示。

由表3可知,采用加权融合算法的双声道气体超声流量计测量结果与采用改进的卡尔曼分布式融合的双声道气体超声流量计检定结果所有流量点都符合准确度等级1.0级的要求,而采用改进的卡尔曼分布式融合的双声道气体超声流量计测量误差为-0.58%,重复性为0.21%,其测量结果优于加权融合算法。

表3 双声道气体超声流量计流量对照实验Tab.3 Flow comparison experiment of double-channel ultrasonic flowmeter m3·h-1

7 结 论

本文设计了一种双声道气体超声波流量计的数据融合方法。首先将两个声道测量的时差数据分别采用格拉布斯准则进行粗大误差剔除,然后采用算术平均值和中值相结合的方法进行流量计算和分段修正,从而计算每个声道的流量。最后,通过对管路内流量变化状态及声道故障诊断,采用改进的卡尔曼分布式融合算法计算出管道内的流量,实现了双声道超声波流量计的数据融合。最终的实验结果表明,该数据融合方法具有较好的数据处理效果和性能,具备判断管路内流量变化情况和声道的故障功能。