基于流形正则化的批量分层编码极限学习机
2021-09-07杨有恒王卫涛刘浩然
刘 彬,杨有恒,刘 静,王卫涛,刘浩然,闻 岩
(1.燕山大学 电气工程学院,河北 秦皇岛 066004;2.燕山大学 信息科学与工程学院,河北 秦皇岛 066004)
1 引 言
极限学习机[1](extreme learning machine,ELM)作为机器学习中一项重要分支,被广泛应用于图像分类[2]、数据挖掘[3]、工业预测[4,5,16]等各个领域。随着神经网络算法的不断发展,使用ELM进行图像分类越来越受到重视,并且在理论和应用方面都做出了突出的贡献。Kasun等[6]基于ELM自动编码器(autoencoder,AE)的堆叠式模型构建多层神经网络,提出多层极限学习机(multi-layer extreme lea-rning machine,ML-ELM),具有良好的分类性能;Tang等[7]结合多层感知器的分层学习结构和l1范数自动编码器提出分层极限学习机(hierarchical extreme learning machine,H-ELM),实现了更好的特征提取。然而,上述算法在面对庞大且复杂的训练数据时[8]:由于数据量呈指数增加,但内存的增长跟不上数据的增长,从而导致算法由于内存的限制,很难测试更多的隐藏节点以获得最佳性能。目前,针对上述问题有2种解决方法:1)使用物理内存大的超级计算机,然而,超级计算机在硬件和功耗上都是非常昂贵的,并不总是为许多研究人员所用。2)融合其他特征降维方法,比如,文献[9]基于PCA和ELM-AE,通过减少每一层的隐藏节点数,提出堆叠式极限学习机(stacked extreme learning machine,S-ELM),具有更高效的非线性数据处理能力;文献[10]基于核方法提出基于经验核映射的多层极限学习机(empirical kernel map-based multilayer extre-me learning machine,ML-EKM-ELM),克服了传统算法存在的内存存储和计算问题;文献[11]采用LLTSA算法将训练样本和测试样本的高维向量压缩为具有更好区分性的低维向量,增强了数据的自适应性,为快速训练ELM分类器提供更低内存消耗。尽管这些方法均实现了减少运行内存的目的,但是增加的算法无疑会导致计算复杂度的上升和模型结构复杂度的增加,从而使运算时间变长、学习速度变慢。因此,在有限的内存条件下,适当减少内存使用对提升算法的性能是十分有必要的。
本文针对极限学习机在处理高维数据时能耗大、分类准确率低等问题,提出了基于流形正则化的批量分层编码极限学习机(batch hierarchical coding extreme learning machine,BH-ELM)算法。本算法对数据集进行分批处理,以减少数据维度和降低数据复杂程度,同时利用多层自动编码器对数据进行无监督编码,实现深层特征提取;进而结合流形正则化框架,通过推导新的输出权重公式来构造含有继承因子的流形分类器,实现模型的求解。
2 极限学习机
对于N个样本(xi,ti),其中xi=[xi1,xi2,…,xiN]T,ti=[ti1,ti2,…,tiN]T,则标准单隐层前馈神经网络(single hidden layer feedforward neural network,SLFN)可以表示为[12]:

(1)
式中:g(·)为激活函数;β=(β1,β2,…,βL)T为连接第i个隐藏节点和输出节点的权重向量,L为隐藏层节点数;ai为连接第i个隐藏节点与输入节点的权重向量;bi为第i个隐藏节点的偏置;ai·xi表示ai和xi的內积。SLFN学习的目标是使得输出误差最小,可以表示为:
(2)
即存在ai,bi使得:
(3)

β=H+T
(4)
式中H+为输入样本的隐藏层输出矩阵。

图1 传统ELM模型Fig.1 Traditional ELM model
通过建立最小化损失函数,则ELM的目标函数可以表示为:
(5)
式中:C为正则化最小均方参数;ξi为输出误差。根据训练数据集大小,可得输出权重β的不同解为:
(6)
在式(6)的矩阵运算中,HTH为矩阵HT每行N个元素和矩阵H每列N个元素逐个相乘得到的一个维度N×N的对角阵,其计算复杂度为O(N2L),而求逆运算的计算复杂度为O(N3),当样本数量N较大时,输出权重矩阵β的维数大大增加,使得训练广义模型所需的隐藏节点数量骤增。同时随着网络规模变大,导致传统ELM因计算复杂度和内存需求增加而难以具有较好的性能。
3 BH-ELM算法
为有效解决高维数据处理问题,本文受分层学习和分批训练思想的启发,提出BH-ELM算法,其训练模型如图2所示,该算法训练体系结构分为3个独立的阶段:
1)数据批次化;
2)无监督分层特征编码;
3)有监督的特征分类。
对于第1阶段,为缓解训练数据的维数灾难问题,在分层学习基础上引入数据批处理思想,首先将高维数据X均分为M个批次,以降低输入数据维度和数据的复杂程度;对于第2阶段,为获得更有效的稀疏特征,采用基于l1范数的ELM-AE数据挖掘方法,通过多层自动编码器对数据进行无监督编码;对于第3阶段,为提高算法的泛化能力,利用含有继承因子的流形分类器作为ELM决策层输出。
本文优化模型立足于网络整体,通过分层学习将有监督学习和无监督学习结合起来共同挖掘高维数据分布的几何结构,其独特的数据批处理过程和双隐藏层结构,在宏观上实现内存消耗和算法低复杂性的双重优化,达到提高模型稳定性和分类准确率的目的。

图2 BH-ELM训练模型Fig.2 BH-ELM training model
3.1 数据批次化
由于一次性将输入矩阵用来训练的运算量要远远大于分批训练的运算量,这对内存和CPU处理能力是一个很大的考验。因此,本文提出数据批处理过程,其训练过程如图3所示。

图3 数据批次化训练过程示意图Fig.3 Schematic diagram of data batch training process
由图3可知,当前样本数据的输出权值βk+1的计算依赖于前一批样本的输出权值βk,而每一批样本数据的隐藏层输出矩阵H之间的更新则相互独立。因此先对矩阵H进行并行化处理,然后建立各批次之间的函数关系,再对β进行串行更新,以增强样本点之间的继承关系,降低输入数据规模。
3.2 无监督编码器
双层无监督编码的训练过程,目的是将编码后重建的特征矩阵与前一层的特征矩阵并行连接,使特征在不同维度上叠加,从而实现深层特征提取。此外,为获得有效的输入特征,在优化目标中加入稀疏约束。与传统ELM-AE不同,本文在优化目标函数中用l1范数惩罚代替l2范数惩罚,其中基于l1范数的自动编码训练过程为:
(7)

为使BH-ELM具有较快的收敛速度,采用快速迭代收缩阈值算法(FISTA)[13]求解,其步骤如下:
Step1:取y1=β0∈Rn,t1=1,设定步长为0.5;
Step3:计算

通过步骤Step3的j次迭代,可以有效重构样本数据并映射到低维空间,以降低输入数据的矩阵维度。
3.3 流形正则化框架
流形正则化是一种基于流形学习的约束,其作用是使数据在新的投影空间中能够保持在原特征空间的非线性几何结构,直观的揭示出高维数据空间分布在低维流形子空间上的内在规律,目前已经大量应用于图像分类领域[14,15]。

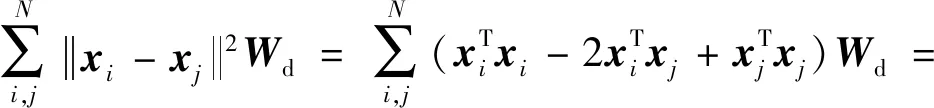
(8)
3.4 批次监督分类器
在求解式(5)的广义特征值问题时,为保证数据的完整性,本文引入了继承因子,通过建立各批次的输出权重关系,构建了批次继承学习范式,则优化函数可由式(5)改写为:
(9)
式中:w为第1批数据得到的初始输出权重;u为继承因子,用以调节各批次之间输出权重的比例;i=1,2,…,N。
为进一步提升训练速度和处理效率,在分类决策阶段,将原始ELM分类器替换为含有继承因子的流形分类器作为输出,即在基于约束优化的批次ELM函数范式中引入流形正则化框架,参考式(9)可以构造凸可微的目标函数为:
(10)
则求解输出权重β转化为求解最小值优化问题,通过求导可得目标函数中β的梯度为:
=β+HTC(T-Hβ)+u(β-w)+λHTLHβ
(11)
当N≥L时,
β=(I+HTCH+uI+λHTLH)-1(HTCT+uw)
(12)
当N β=(HTCT+uw)(I+CHHT+uI+λLHHT)-1 (13) 式中:I为单位矩阵。 由于N≥L,故本文使用式(12)作为输出权重的更新表达式。 本文BH-ELM算法的训练步骤。 输入:设N个训练样本(xk,tk),k=1,…,N,其中xk为第k个样本,tk为xk的目标向量。 数据批次化 1)将数据集平均分割为M份,其中第i份样本数据记为Xi; 2)随机生成输入权值ai和隐藏层偏置bi,其中i=1,2,3; 无监督编码部分 3)将第1批数据导入无监督编码部分,并在输入数据中引入标签a,即Hi=[Xia]; 4)计算Ai=(Hi·bi)并调整范围为[-1,1]; 5)计算各层输出权值βi=AE(Ai,Hi); 6)计算各层近似映射Ti=(Hiβi); 7)调整Ti,缩放范围至[0,1],返回步骤2); 输出:完成双层无监督编码训练,输出为T; 监督分类部分 输入:无监督编码的输出T是监督分类部分的输入; 8)在输入数据中引入标签a,计算Hj=[Tja]; 9)计算Tj=g(Hj·wj); 11)返回步骤3),将其余M-1批数据导入无监督编码部分,执行上述步骤4)到步骤10); 输出:根据式(12)更新相邻批次输出权重,直到完成监督分类。 为验证本文BH-ELM算法的优越性,采用NORB,MNIST和USPS测试数据集[9]进行实验。本次实验均在一台处理器配置参数为Intel Xeon Silver 4110@2.1 GHz,内存为64 GB,软件环境为64位Matlab R2018a的计算机上运行完成。实验数据集具体描述如表1所示。 表1 实验数据集Tab.1 Experimental data set 为考察正则化最小均方参数C和隐藏层节点数L对BH-ELM分类准确率的影响,以NORB数据集为例,选择C的取值范围为{10-5,10-4,…,104},L的取值范围为{100,200,400,…,2000},得到超参数C和L对BH-ELM分类准确率影响的变化曲线分别为图4和图5所示。 图4 正则化参数C对准确率的影响Fig.4 The effect of regularization parameter C on accuracy 图5 节点数L对准确率的影响Fig.5 The effect of the number of nodes L on accuracy 由图4和图5可知,其中参数C和L对BH-ELM性能的影响是不同的。在考察其中某一参数对分类准确率的影响时,其它参数应保持不变,如图4,当L=2 000时,随着C的增加,BH-ELM的分类准确率先增加后减少,当C=10-1时,达到最大值。如图5,当C=10-1时,随着L的增加,BH-ELM的分类准确率随之增加,这说明本文算法的最高分类准确率由隐藏层节点数决定。当隐藏层节点较少时,无法充分训练,达不到较高的分类准确率。 对于传统ELM,当隐藏层节点数目较多时,在内存方面会消耗更多的存储空间,导致分类准确率降低,而本文算法具有低内存消耗的特性,能有效控制分类准确率达到稳定范围内较大的隐藏层节点数,使模型分类效果达到最佳。因此,在4.3节实验中选取准确率达到稳定范围内较大的隐藏层节点数。 为验证本文算法的有效性和可靠性,选择具有典型代表性的基于ELM的对比算法:ML-ELM、S-ELM和H-ELM,激活函数均采用sigmoid函数。以MNIST数据集为例,在同一实验条件下,根据训练集样本大小的变化,得到4种算法的分类准确率曲线如图6所示。 图6 训练集大小与准确率的关系Fig.6 The relationship between training set size and accuracy 由图6可知,分类准确率随训练样本占比的增加而增加,随着训练数据的增多,本文BH-ELM算法和其它3种算法的分类准确率都呈上升趋势。同等数量的训练样本下,相比于其它3种算法,本文算法的分类准确率始终处于高识别率状态,这说明本文算法是可行并有效的。在训练样本占比较低时,同样能够得到较高的准确率,这说明本文算法具有良好的泛化性能。 为进一步验证隐藏层节点数L对BH-ELM算法性能的影响,比较本文算法与ML-ELM、S-ELM和H-ELM算法在3个测试数据集上的峰值内存消耗量和分类准确率,如图7和图8所示。 图7 4种算法准确率对比Fig.7 Accuracy comparison of four algorithms 图8 4种算法平均峰值内存消耗对比Fig.8 Comparison of memory consumption of four algorithms 其中平均峰值内存消耗量是各算法独立运行30组试验结果,标准差是各组统计的峰值内存消耗量通过式(14)计算得到的。内存消耗方差反映了算法稳定程度,方差越小则说明算法的稳定性越好。 (14) 式中:N为算法独立运行的次数;xi为每次运行的峰值内存消耗值;μ为各组的内存消耗均值。 由图7可知,随着节点数L的增加,4种算法的分类准确率先增加,然后趋于稳定。当L达到10 000 时,本文BH-ELM算法在3种数据集上的分类效果均取得最优,在NORB,MNIST和USPS数据集上的分类准确率分别可以达到92.16%、99.35%和98.86%。 由图8可知,当节点数L相同时,本文BH-ELM算法的平均峰值内存消耗量在3种数据集上均取得最低,且内存消耗方差值明显小于ML-ELM、S-ELM和H-ELM。同时,由图8(a),8(b)和图8(c)可知,当节点数L不同时,BH-ELM算法的平均峰值内存消耗量和方差同样低于其它3种ELM算法,这表明本文算法具有更好的稳定性。 针对高维数据训练的在线内存需求,提出了一种基于流形正则化的批量分层编码极限学习机算法。该算法通过数据批处理引入继承因子,建立了各批次之间的函数关系;通过在逐层无监督训练中引入基于l1范数的稀疏编码,构建了多层ELM-AE网络;结合流形正则化框架,设计了含有继承项的流形分类器。理论分析及仿真结果表明,本文算法分类准确率高、稳定性好、泛化性能强。在保证分类精度的情况下,有效降低了计算量和内存消耗,为ELM克服维数灾难问题提供了参考。3.5 算法步骤
4 实验结果与分析

4.1 超参数的影响


4.2 泛化性能分析

4.3 分类准确率与内存消耗对比

5 结 论
