基于改进狮群算法的汽轮机热耗率模型预测
2021-09-07汪婵婵
汪婵婵
(浙江安防职业技术学院 信息工程系,浙江 温州 325016)
1 引 言
汽轮机发电组将机组每产生l kW·h所消耗的热量定义为机组热耗率,并作为衡量电厂热经济性的重要标准。如何降低热耗率,提高机组运行效率,对电厂节能减排具有重要的意义[1]。
研究表明,汽轮机热耗率与其影响因素之间存在强耦合以及复杂的非线性关系,因此导致传统的预测建模方式无法精确建立热耗率预测模型。一些学者通过采用回归算法对热耗率值进行预测和计算。左智科等提出了一种基于反馈鲸鱼算法与支持向量机的综合建模方法,对热耗率进行预测计算[2];王莉莉等提出了一种基于混沌粒子群与最小二乘支持向量机的综合建模方法,对热耗率进行分析并建立预测模型[3];此外,还有基于共生算法与极限学习机的综合建模方式[4,5]、基于果蝇优化算法与最小二乘支持向量机的热耗率预测建模策略[6]、基于BP神经网络的热耗率在线计算策略[7]等。以上预测模型具有较高的预测精度和较强的鲁棒性。然而,针对传统神经网络具有训练速度慢以及泛化能力差的缺陷,通过单一优化机制寻优的群智能优化算法难以有效提高神经网络的预测性能。
针对上述缺陷,本文提出一种基于改进狮群算法[8]和快速学习网的综合建模方法,引用黄金正弦等策略对算法进行改进,并将改进的狮群算法优化快速学习网模型权值和阈值,最后将优化后的快速学习网进行机组热耗率预测实验。
2 基本概念
2.1 快速学习网
快速学习网(fast learning network,FLN)是Li G Q提出的一类新型前馈神经网络[9],其优点在于输出层不仅接收隐含层的信息,同时也接收输入层的信息。其中隐含层对于输出层的信息传递呈非线性,输入层对输出层的信息传递则具有线性关系,从而组成一类具有线性和非线性的双并联组合神经网络模型。
设观测样本总数为N,则有(xi,yi),i=1,2,…,N,xi为第i个观测样本的第n维输入向量,则输入向量矩阵xi为xi=[xi1,xi2,…,xin]T,n为输入节点个数;yi为第i个观测样本的第s维输出向量,则输出向量矩阵yi为yi=[yi1,yi2,…,yis]T,s为输出层节点个数。定义隐含层中神经元总数为m,激励函数为g(x),快速学习网的数学模型为:
(1)

为了方便计算,现设输出权值矩阵为W=[WioWoh]s×(m+n),隐含层输出矩阵为

2.2 基本狮群优化算法
狮群优化算法是模拟狮群狩猎所提出的一类新的群智能优化算法[8],该类算法将狮群分为狮王、母狮和幼狮3类,分别进行位置更新。算法在寻优初始阶段,对狮群位置进行初始化,其数学表达式为:
Xi=(Xi,1,Xi,2,…,Xi,D)
(2)
式中:i=1,2,…,NP,NP为狮群的种群规模;D为维数;Xi为第i个狮子所在位置。
首先,狮王始终围绕最佳猎物进行小范围移动,确保食物源在自己附近,其位置更新公式为:
(3)

其次,母狮在捕食过程中通常会采用协同狩猎的方式进行抓捕猎物,这种行为可被描述为:
(4)

(5)
式中:Jmax和Jmin为狮群个体各维度的最大均值和最小均值;Tmax为最大迭代次数。
最后,幼狮按母狮和狮王的位置进行选择性移动,其计算方式为:
(6)
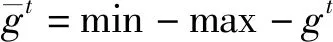
3 改进狮群优化算法
基本狮群优化算法的优点在于算法具有较强的局部搜索能力,调整参数少,易于实现;但其缺点在于算法全局搜索能力较差,在迭代后期易早熟收敛陷入局部最优,且算法在迭代后期收敛速度较慢。本文针对上述缺陷,提出一种改进的狮群优化算法(improvement lion swarm optimization,ILSO)。
3.1 非线性扰动因子
研究表明,较大的惯性权重会帮助算法获得较高的全局勘探能力,较小的惯性权重有助于提高算法的局部开发能力[10]。在传统狮群算法迭代过程中,幼狮在狩猎时均在限定范围内搜素猎物,在算法中表现为幼狮范围扰动因子呈线性递减趋势。但遵循线性递减规律的扰动因子无法满足算法在迭代过程中的实际情况。因此本文引用对数函数,对线性扰动因子进行改进,使扰动因子非线性化。改进后的非线性扰动因子的数学表达式如式(7)所示,其控制曲线如图1所示。
(7)
式中:Tmax为算法最大迭代次数;t为当前迭代次数;0.55和0.247为实验200次后求得的最佳系数。

图1 非线性控制因子Fig.1 Nonlinear perturbation factor
由图1可知,设最大迭代次数为100,前70次迭代时,非线性控制因子取值较大,并且快速非线性递减,目的是使ILSO算法具有较快的收敛速度,同时可获得较强的全局勘探能力。在70次迭代到100次迭代时,非线性控制因子较小,且递减速度减慢,使得算法可以在迭代后期获得较高的收敛精度。由于单纯的对数函数会导致算法后期收敛过慢,陷入局部最优,因此采用分段的形式对控制因子进行改进,防止算法在迭代后期早熟收敛,陷入局部最优。
3.2 禁忌搜索
传统狮群优化算法中,狮王总是围绕最佳食物源进行移动,且算法在每次迭代过程中,所有种群个体的位置均由狮王的位置来更新,使得算法在迭代初期可以快速接近最优解,很大程度提高了算法的收敛速度。但在算法迭代后期,当狮王陷入局部最优时,其余狮群个体均围绕当前最佳位置进行个体更新,同样无法跳出局部最优,最终导致算法早熟收敛,陷入局部最优。因此本文在算法迭代过程中引入禁忌搜索策略[11]。
禁忌搜索的核心是建立禁忌表,通过标记过往的搜索记录,避免算法在一段迭代过程中回到原始解。将禁忌搜索策略引入狮群算法的优点在于,当算法在迭代后期,陷入局部最优时,可使算法回到局部极值点,帮助算法跳出局部最优。其搜索流程为:
Step1:计算狮群中每个个体的适应度值,并将最优值记为当前最优解;
Step2:在当前最优解的设定领域内,随机选取候选解集合;
Step3:判断当前候选解是否存在于禁忌表中,是则跳转到Step4,否则跳出当前迭代;
Step4:计算候选解的适应度值,并与当前最优解的适应度值进行对比;若候选解的适应度值优于当前最优解的适应度值,则将当前候选解更新为当前最优解,更新禁忌表;
Step5:判断是否达到最大禁忌搜索次数,是则输出最优解,否,则返回Step2。
3.3 黄金正弦
由于狮群优化算法的更新机制较为复杂,很大程度影响了算法的收敛速度,因此本文引入黄金正弦策略,加快算法的收敛速度,解决算法在迭代后期收敛速度慢导致停滞的问题。黄金正弦是学者Tanyildizi E提出的一类以正弦函数为基础的元启发优化算法[12]。其优点在于算法收敛速度快,且具有较强的鲁棒性,算法通过遍历单位圆上的所有点,并在搜索过程中引入黄金分割系数,确保只扫描可能产生全局最优解的搜索区域,极大程度提高了搜索速度。其更新过程为:
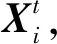

Step3:在t+1次迭代过程中,更新第i个个体的位置,其更新公式为:
(8)
式中:R1为0~2π之间的随机数;R2为0~π之间的随机数。分别决定粒子在下次迭代过程中的移动距离和移动方向。x1和x2为黄金分割系数:
x1=-π+(1-δ)·2π
(9)
x2=-π+δ·2π
(10)
(11)
因此,本文的ILSO算法流程为:
Step1:种群初始化;
Step2:计算狮群中每个个体的适应度值,并将最优值记为当前最优解;
Step3:通过式(3)、式(4)和式(6)对粒子进行位置更新,再次计算狮群中每个个体的适应度值,更新当前最优解;
Step4:在当前最优解的设定领域内,随机选取候选解集合;
Step5:判断当前候选解是否存在于禁忌表中,是则跳转到Step6,否则执行黄金正弦操作;
Step6:计算候选解的适应度值,并与当前最优解的适应度值进行对比;若候选解的适应度值优于当前最优解的适应度值,则将当前候选解更新为当前最优解,更新禁忌表;
Step7:判断是否达到最大禁忌搜索次数,是则输出最优解,否,则返回Step4。
Step8:判断是否达到最大迭代次数,是则输出全局最优解,否,则返回Step2。
4 ILSO算法性能测试
4.1 ILSO、LSO、IPSO-TS和GSASO性能比较
为了验证本文所提ILSO算法的性能,选取12个基准函数作为测试函数,对ILSO算法进行验证,测试函数见表1。

表1 12个基准测试函数Tab.1 12 benchmark functions
为了能更直观地看出本文所提改进策略对LSO算法搜索精度的提高,本文将ILSO算法的实验结果与基本狮群优化算法(LSO)[8]、基于禁忌搜索的改进粒子群算法(IPSO-TS)[13]和基于黄金正弦的混合原子算法(GSASO)[14]的实验结果进行对比。为了保证对比结果实验的公平性,4种算法的参数一致,种群规模均取为100,最大迭代次数均取为500,维数均取为50。GSASO算法中的深度加权系数α=50,乘数权重β=0.2。4种算法独立运行20次,记录结果的平均值ave和标准差std,实验结果见表2。

表2 12个测试函数的测试结果对比Tab.2 Comparison of test results of 12 test functions
由表2可知,对于单峰测试函数f1~f4而言,本文所提ILSO算法取得实验结果最优,说明ILSO算法相较其他3种算法具有更强的局部开发能力;同时,对于测试函数f2而言,当LSO算法和GSASO算法陷入局部最优时,ILSO算法仍能求解到更好的解,说明ILSO通过引入禁忌搜索策略,很大程度提高了算法跳出局部最优的概率;此外,相较其他算法,ILSO算法求解的平均值和标准差最小,说明ILSO算法具有较强的收敛精度,鲁棒性更强。
对于多峰测试函数f5~f8而言,本文所提ILSO算法在测试函数f6和f7上取得结果最优,但在测试函数f5和f8上的结果略低于GSASO算法,但仍优于LSO算法。说明加入黄金正弦策略后,ILSO算法在很大程度上提高了算法的收敛速度和全局收敛能力。与LSO算法相比,ILSO算法的收敛精度更高,更好地平衡了算法的全局勘探能力和局部开发能力。
对于固定维函数而言,由于维数的降低,4种算法的寻优精度和算法整体性能均有所提高,说明4种算法在处理简单优化问题上,均有较高的收敛精度,但本文所提ILSO算法可以取得更高的平均值,说明相较其他3种算法,ILSO算法具有更强的鲁棒性,算法稳定性更高。
整体而言,加入黄金正弦策略和禁忌搜索策略后,ILSO算法很大程度提高了全局搜索能力和局部搜索能力,相较单一机制的黄金正弦算法与禁忌搜索算法而言,ILSO算法的整体性能更优;此外非线性扰动因子的加入,更好地帮助ILSO算法平衡了算法的全局收敛能力和局部收敛能力。
4.2 ILSO、QBSA、AWOA和A-KH性能比较
本文将所提算法ILSO用于在线计算FLN的阈值和权值,并将ILSO-FLN模型应用于电厂热耗率模型预测。为了更好地验证ILSO的有效性,本文将ILSO算法的数值实验结果与其他3类热耗率模型预测算法中的群智能算法(QBSA)[15]、(AWOA)[16]和(A-KH)[17]的数值实验结果进行对比,4种算法的种群规模均取为100,最大迭代次数均取为500,维数均取为50。4种算法独立运行20次取平均值和标准差,具体实验结果见表3。
由表3可知,对于单峰测试函数而言,本文所提ILSO算法在测试函数f1、f2和f4上取得的测试结果均优于其他3种算法,在f3上的结果略差于AWOA算法,但相差不大,说明4种算法相比,ILSO算法具有更高的收敛精度和收敛稳定性,局部开发能力更强。
对于多峰测试函数而言,ILSO算法在测试函数f6和f7上取得的结果最优,在f5上的结果略差于A-KH算法,在f8上的结果略差于AWOA算法;但总体而言,ILSO算法的收敛速度更快,全局搜索能力更强。对于固定维函数而言,4种算法的收敛结果相差不大,对于测试函数f11和f12而言,更是可以求得理论最优值,说明ILSO算法的整体性能较为平衡,鲁棒性较强。

表3 12个测试函数的测试结果对比Tab.3 Comparison of test results of 12 test functions
5 热耗率模型预测实验
5.1 基于ILSO-FLN的热耗率预测模型建立
以文献[18]中的主蒸汽压力、温度以及给水流量等12个参数为预测模型的输入,以热耗率为预测模型输出,选取某热电厂600 MW超临界汽轮机组作为被控对象,建立汽轮机组模型,验证本文所提ILSO-FLN的预测能力。部分测试数据见表4。表4中,Ne为发电负荷,P0为主蒸汽压力,T0为主蒸汽温度,Pr为再热器出口蒸汽压力,Tr为再热器出口蒸汽温度,Ph为再热器入口蒸汽压力,Th为再热器入口蒸汽温度,Dz为再热减温水流量,Dgl为过热减温水流量,Pb为汽轮机背压,Tc为循环水进水口温度,Dfw为给水流量。

表4 部分采集数据Tab.4 Part of collected data
研究表明,FLN的权值和隐含层阈值对于预测效果有较大影响,随机初始化FLN的权值和阈值难以保证FLN对汽轮机热耗率进行有效预测。针对上述问题,本文采用ILSO算法对FLN输入权值和阈值进行在线优化,以ILSO算法是否达到最大迭代次数为预测终止条件,输出的最优解即为FLN预测模型的输入权值和隐含层阈值,其中算法寻优的适应度函数为:
(12)

(13)
5.2 预测结果分析
本文从145组测试数据中心随机选取120组数据作为训练样本,其余25组测试数据作为测试样本,用于验证ILSO-FLN预测模型的预测精度和泛化能力。采用FLN与ILSO算法对热耗率进行综合建模,其预测模型流程见图2所示。

图2 基于FLN与ILSO预测模型的预测流程Fig.2 Prediction process based on FLN and ILSO model
将预测结果与AWOA-FLN、A-KH-FLN和QBSA-FLN的预测结果相比较,具体结果见图3所示。同时,针对训练样本,ILSO-FLN的相对预测误差见图4所示。
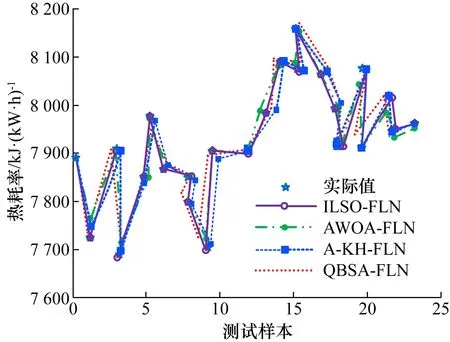
图3 测试样本预测值与实际值对比图Fig.3 Comparison of data between prediction results and action measurements

图4 ILSO-FLN训练样本相对预测误差Fig.4 The relation error of ILSO-FLN forecast
由图3可得,将本文ILSO-FLN预测模型的预测结果与AWOA-FLN、A-KH-FLN和QBSA-FLN预测模型的预测结果对比,ILSO-FLN的预测精度远优于其他3种预测模型的预测精度,且ILSO-FLN预测模型的泛化能力也远强于其他3种预测模型的泛化能力。
由图4可知,ILSO-FLN对于训练样本的相对误差最大仅为4.27%,且曲线波动较小,说明ILSO-FLN预测模型针对训练样本的热耗率预测精度较高。
为了更好地体现ILSO-FLN算法的预测精度,本文选取均方根误差RMSE、平均绝对误差MAE以及平均相对误差MAE为评价指标[18],对FLN、ILSO-FLN、AWOA-FLN、A-KH-FLN、QBSA-FLN及PSO-ELM的预测性能进行评价,评价结果见表5。
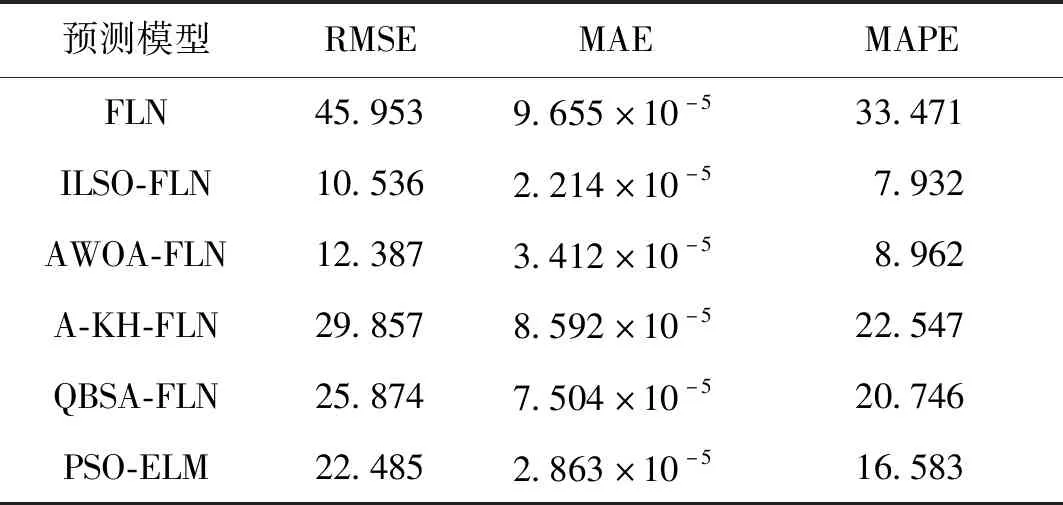
表5 测试样本准确度对比Tab.5 Accuracy comparison of test data
RMSE值越小,预测精度越高;MAE和MAPE的值越小,证明预测结果越接近实际值。由表5可知,本文所提ILSO-FLN预测模型的RMSE值小于其他5种预测模型,并且远优于FLN预测模型,说明ILSO-FLN预测模型的预测精度最高;同时,ILSO-FLN预测模型的MAE和MAPE的值仅为2.214×10-5和7.932,远低于FLN、AWOA-FLN、A-KH-FLN和QBSA-FLN预测模型的MAE和MAPE值,说明ILSO-FLN的预测结果更接近实际值;此外,针对ASOS-ELM而言,ILSO-FLN的预测精度和泛化能力与ASOS-ELM的预测精度和泛化能力相差不大,但仍略优于ASOS-ELM的预测精度。因此ILSO-FLN预测模型相较其他几种预测模型具有更高的预测精度和泛化能力。
图5展示了AWOA-FLN、A-KH-FLN、QBSA-FLN以及本文所提ILSO-FLN 4种预测模型对测试样本的预测误差的对比结果。由图可知,ILSO-FLN预测曲线波动相较其他3种预测模型的预测曲线波动较小,说明ILSO-FLN预测模型的预测稳定性更强;同时,ILSO-FLN模型的预测最大误差仅为25 kJ/kW·h,远低于其他3种预测模型的预测误差,因此本文所提ILSO-FLN算法相较其他3种模型具有更高的预测精度,可以更精确预测热电厂汽轮机的热耗率。
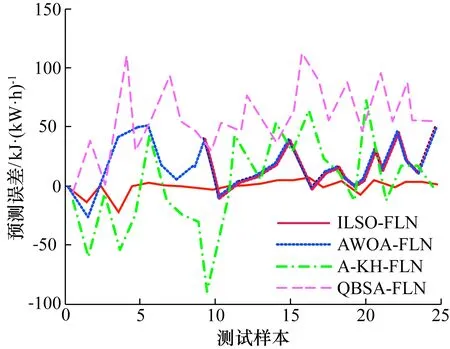
图5 预测误差曲线Fig.5 The forecast error curves
6 结 论
本文针对热电厂汽轮机热耗率预测问题,提出了一种基于改进狮群优化算法的快速学习预测模型。针对传统狮群算法全局搜能力差,收敛精度低等问题,采用非线性扰动因子、黄金正弦以及禁忌搜索策略进行改进。通过数值仿真实验,对ILSO算法进行验证,实验结果表明,ILSO算法具有更高的收敛精度和更快的收敛速度;以汽轮机为研究对象,建立ILSO-FLN预测模型,对热耗率进行预测实验,并将实验结果与其他几种预测模型的预测结果进行对比,对比结果显示,ILSO-FLN预测模型具有更高的预测精度和泛化能力,是一种更加理想的热耗率预测方法。
