基于㶲评估的多能流节能调度

吴晨曦，何章露，叶剑雄，洪晗笑

基于㶲评估的多能流节能调度

吴晨曦，何章露，叶剑雄，洪晗笑

（杭州电子科技大学 自动化学院，浙江 杭州 310018）

多能流系统可以实现能源的整体规划、多能互补和梯级利用，提高能源利用率。在此背景下，构建冷、热、电多能流系统模型，并引入压缩空气消纳风电，平衡能量。以热力学第二定律的“㶲分析”方法评估系统的节能指标，确定多能流系统的最节能调度方法。以某园区冬夏季节的典型风电出力和冷、热、电需求为例，采用模拟退火算法进行系统的节能调度并计算系统㶲效率。对系统是否使用先进绝热压缩空气对系统节能性的影响进行对比研究。研究结果表明，系统采用㶲评估节能指标，在具有先进绝热压缩空气时㶲效率更高，约为38%～58%。

先进绝热压缩空气；㶲效率；风电；多能流；模拟退火算法；节能

0 引言

社会生活对能源的需求越来越大，供需关系矛盾逐渐增加，这是社会经济发展、科技生活进步的必然结果。为了保持人类社会发展的可持续性，需要对可再生清洁能源进行充分利用并提高能源利用率避免浪费。其中，新一代能源系统对传统能源系统的一些经典模式进行突破，打破单独设计和独立运行模式的多能流系统和综合能源系统等已经成为当下研究的热点[1-3]。

传统电力系统大多只针对能源的数量进行节能调度，然而对于新一代的多能流系统，输入、输出的能源种类不只有一种，所以在多种能源的调度上，不应该只专注数量的减少，更应该兼顾质量上的节约[4-6]。能量的数量和质量在转换过程中发生变化，热力学第二定律揭示了在该过程中“质”的下降，即能量的品质贬值。能量中可连续并且完全转化为其他任何形式能量的一部分称为㶲[7]。

对能源系统进行热效率分析可以评估系统的能源利用率，而㶲分析法可对系统进行热效率分析。能量在传递和转换的过程中有一定的损耗，㶲分析法基于热力学第一、第二定律，有机结合能量的“量”和“质”，深入描述该过程中能质退化的本质。

现有研究没有考虑在多能流系统中引入先进绝热压缩空气储能系统（AA-CAES，advanced adiabatic compressed air energy storage）进行㶲评估的节能调度。本文根据热力学第二定律，对多能流系统进行建模分析：采用㶲分析法对此系统建立节能指标，对该系统进行㶲效率评估；引入AA-CAES作为储能系统，用模拟退火算法求解系统模型，求解出系统最节能的调度方法。结果表明，系统风电消纳能力得到提高的同时，系统的能源利用率也得到了提高。

1 多能流系统节能调度模型

1.1 多能流系统模型

如图1所示。本文的多能流系统输入能源为可再生分布式能源，如风能和天然气，需求端为冷、热、电负载。为应对风力发电的不确定性，本系统采用AA-CAES方法，不仅可作为平衡风力发电随机性的储能系统[8]，同样可以作为供热设备进行供热。

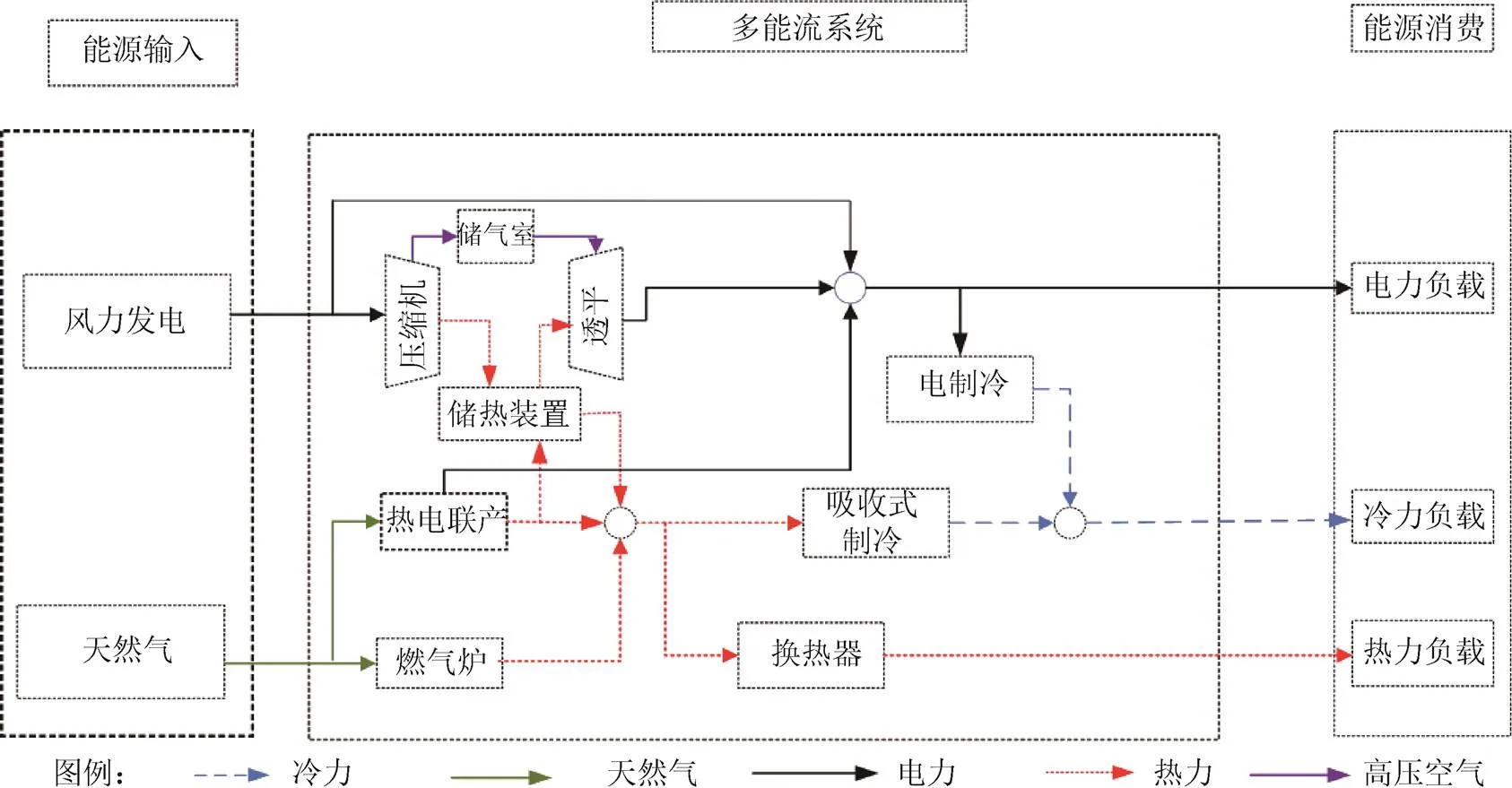
图1 多能流系统模型

1.1.1 AA-CAES电站模型

压缩空气储能系统由空气压缩机、储气系统、膨胀机和储热系统（换热器与储热系统）组成。储能时，利用多余的风电对空气进行压缩，产生压缩热并进行回收，将压缩产生的热能存储和经过压缩后的空气存储进行解耦；释能时，将高压空气和压缩热能输入膨胀机进行发电。AA-CAES最高可达70%[9]的综合效率。

（1）压缩阶段

大部分AA-CAES电站中的压缩机使用多级压缩、级间冷却模式，采用这种模式，每级压缩都被视为可逆绝热过程[10-11]。级压缩的AA-CAES电站在时刻的第级压缩功率为：

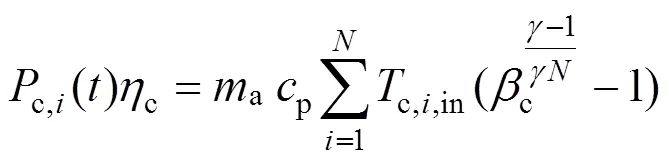
式中：c表示压缩过程效率；通过第级压缩机的空气质量为a；p表示空气的定压比热；c,i,in表示第级压缩机的进气温度；c表示压缩机的额定压缩比；表示空气比热比。

（2）换热阶段

经过换热器和载热介质的压缩热和高温高压空气会进行换热。其中，换热过程的关键参数[12-13]，即换热效能参数定义如式（2）：

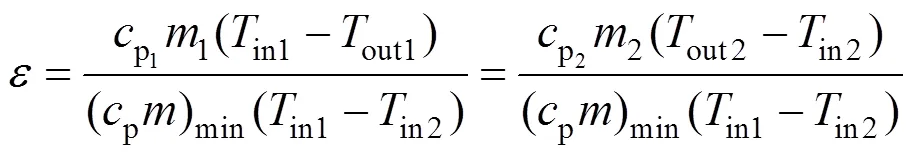
式中：表示流体的质量；表示流体的温度，热、冷流体分别对应含有下标1、2的参数；流体进入和离开换热器分别对应含有下标in、out的参数。

（3）储热阶段

压缩阶段产生的压缩热在经过换热阶段后进入储热装置。在储热过程中，级换热器吸收且存储到储热器中的总热量如式（3）：

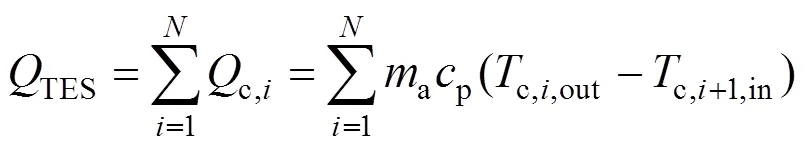
式中：TES表示级换热器吸收且存储到储热器中的总热量；c,i表示第级换热器换热时吸收的热量。

（4）释热阶段

在释能过程，储气室内温度as以及从流入第一级换热器的进气温度近似相等。所以释能阶段第一级膨胀机的进气温度为：

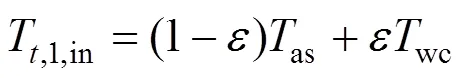
式中：wc为储能阶段储热器中存储热的最高温度。

（5）膨胀阶段

AA-CAES系统在时刻第级膨胀功率为[14]：

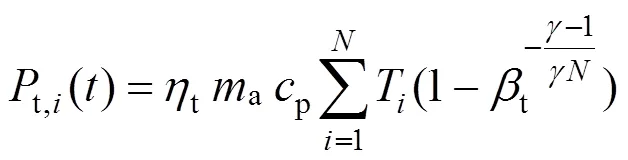
式中：t表示膨胀过程效率；t表示膨胀机额定膨胀比。

1.1.2 CHP机组建模

对于CHP机组，其能源转换关系为：

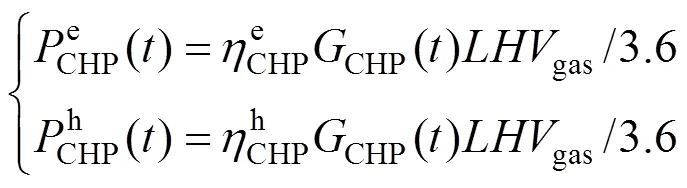
1.1.3 其他建模

燃气炉、吸收式制冷机组和电制冷机组，能源转换描述如下：

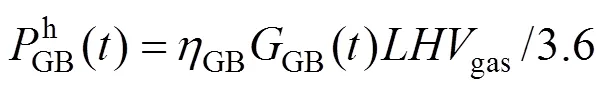
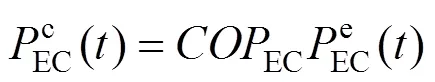
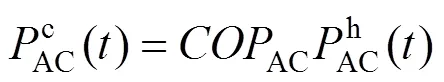
式中：GB为燃气炉的效率；EC和AC分别为电制冷机和吸收式制冷机的性能系数；GB()为时刻燃气锅炉的耗气量。

1.2 目标函数

对多能流系统进行节能调度，其目的不仅仅是节约能量数量，更重要的是质的节省。㶲效率是系统中输入㶲和输出㶲的比值。对各类能源进行㶲分析，即质量评估，目的是实现整个系统㶲效率最大。本文系统模型的能源负载预测结果足够准确，即不考虑负载不确定性。节能目标从系统㶲效率最大转变成系统㶲输入最小。

如图1所示，由风力发电与天然气给冷、热、电负荷供能。在时刻系统的负荷端需求㶲和系统输入端输入㶲的关系为：

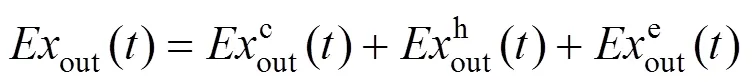
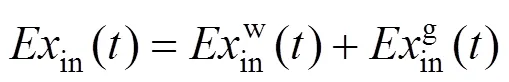
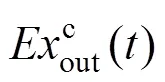
在系统模型中，除了电能是高品位能量，即电能可以完全转换为其他种类能，电能与电㶲相等，其他的冷能和热能相对而言是低品位能量，㶲值小于能值。因此，系统输出端在时刻㶲描述为[15]：

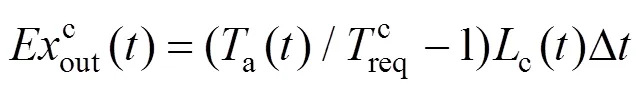
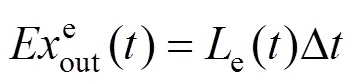
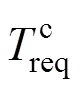
系统输入端输入的天然气中的㶲[22]，可表示为：

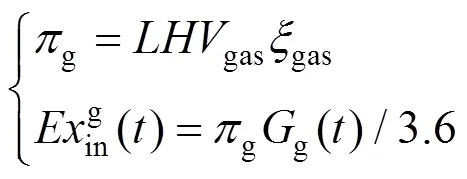
系统输入端的风能是可再生清洁能源，系统输入不关注风能的㶲，而关注风电的㶲。使用AA-CAES平抑风电出力的波动，对风电–压缩空气进行整体性的㶲分析，可表示为：

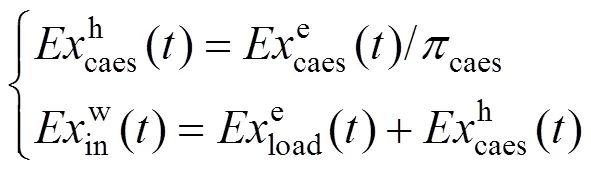
系统㶲效率的计算表示为：

系统的目标函数为：

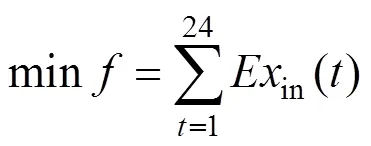
1.3 约束条件

1.3.1 能量约束

系统在以节能为目标的调度过程中，首先需要满足系统冷、热、电的能量平衡约束，既输入的能量一定要满足负载所需的能量。

其中，冷能的能量平衡约束为：

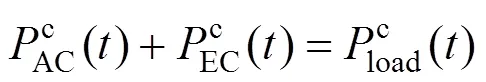
热能负载的能流约束要考虑AA-CAES和系统整体的热量平衡，表示为：

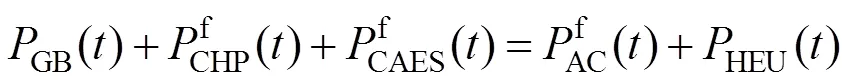
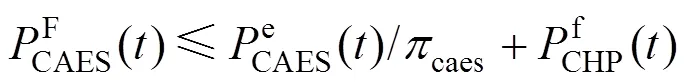
电能的平衡约束为：

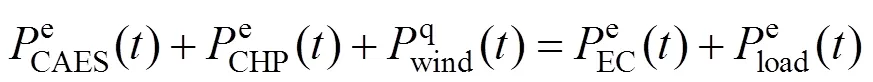
1.3.2 设备约束

CHP机组出力限制和爬坡约束，如下所示：

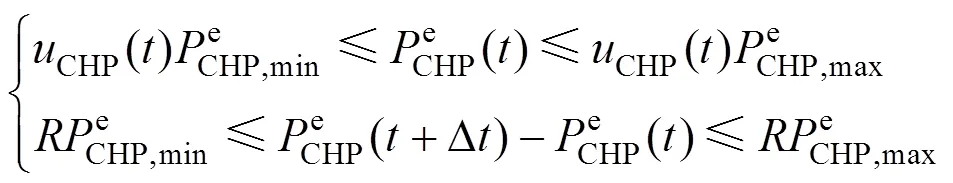
对于燃气炉、电制冷和吸收式制冷机组，考虑其能源转化关系和处理限制约束，模型描述如下：

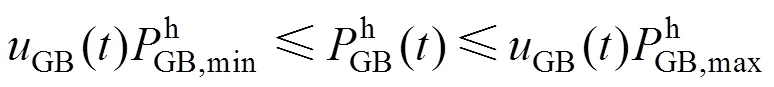
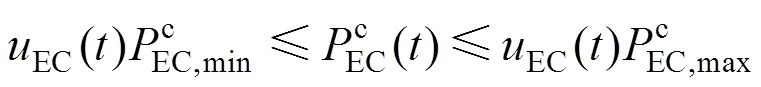
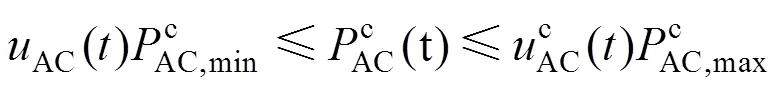
考虑输入输出关系及容量限制，换热器约束表示为：

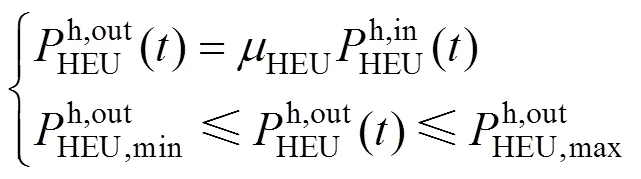
AA-CAES的约束可分别表示为电站充放电功率约束、储气室和储热器约束：

式中：CAESC,min和CAESC,max分别为压缩功率的下上限；C,t为表示压缩工况的二进制变量；CAESG,max和CAESG,min分别为发电功率的上下限；G,t为表示发电工况的二进制变量；st,max和st,min分别为储气室气压的上下限；H,max为储热器储热量的上限值。

2 多能流系统的节能调度

为实现多能流系统的节能调度运行，采用模拟退火算法对上述的多目标优化调度模型进行求解，获得系统最节能的运行方案，即基于㶲评估的最节能运行方案。

2.1 模拟退火法对约束的处理

模拟退火法是一种非线性无约束问题的求解方法，约束条件有不等式约束和等式约束。因此，需要将非线性有约束规划问题转换为非线性无约束规划问题，利用罚函数法将其转化为增广目标函数极小值问题。

目标函数和约束条件可表示为：

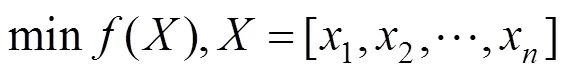
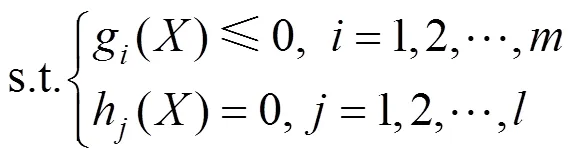
转化为增广目标函数极小值问题后，可表示为：

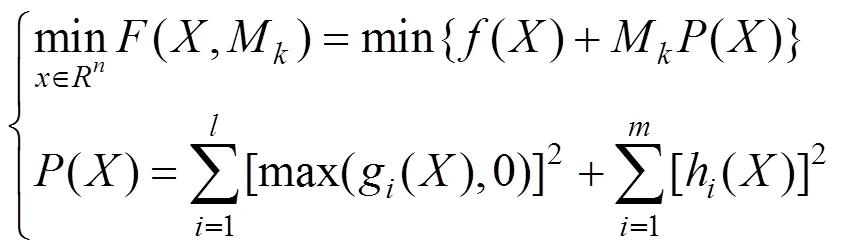
式中：{M}为单调递增的正序列；()为原始的目标函数；()为施加在原始目标函数上的罚函数；M为作用于罚函数的惩罚因子；MP()为惩罚项。在()中，不满足约束条件，惩罚项MP()>0，并且由于{M}单调递增，惩罚项会越来越大。当满足约束条件时，MP()=0，即没有惩罚。因此，当()足够小时，(M)将充分接近约束区域的边界时，可认为(M)是满足约束条件的最小点。

式（30）中的g()为式（21）、式（23）～（26）、式（27）的第二条和式（28）的变化形式，即：

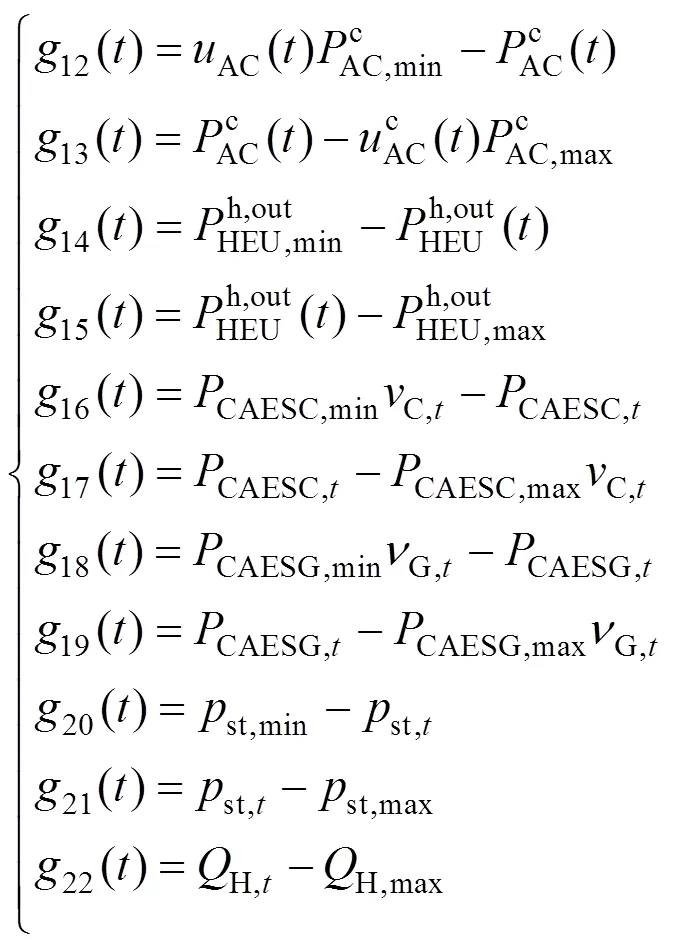
式（30）中的h()为式（18）、式（19）和式（21）的变化形式，即：

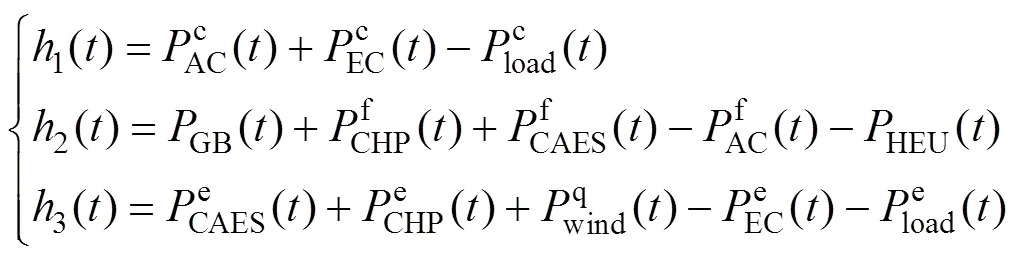
2.2 算法过程

模拟退火算法的核心思想是首先随机选择一个解作为开始，然后产生一个随机扰动，如果找到比上一个解更接近最优解的解，那么直接接受这个解。如果找到的解不如最优解，以一定的概率接受，算法过程如图2所示。

具体步骤如下：

步骤1：初始化迭代次数。温度参数0，参数要足够大，使其对任意一个初始解的接受概率都接近1。

步骤2：令初始可行解等于当前解，计算对应的目标函数值。

步骤3：若此时达到平衡条件，则跳至步骤6；否则执行步骤4和5。

步骤4：进行随机扰动，产生一个试验解new作为的邻域解，new作为其对应的目标函数值。

步骤6：若满足终止条件，则停止迭代；否则，减小温度参数，然后回到步骤3。

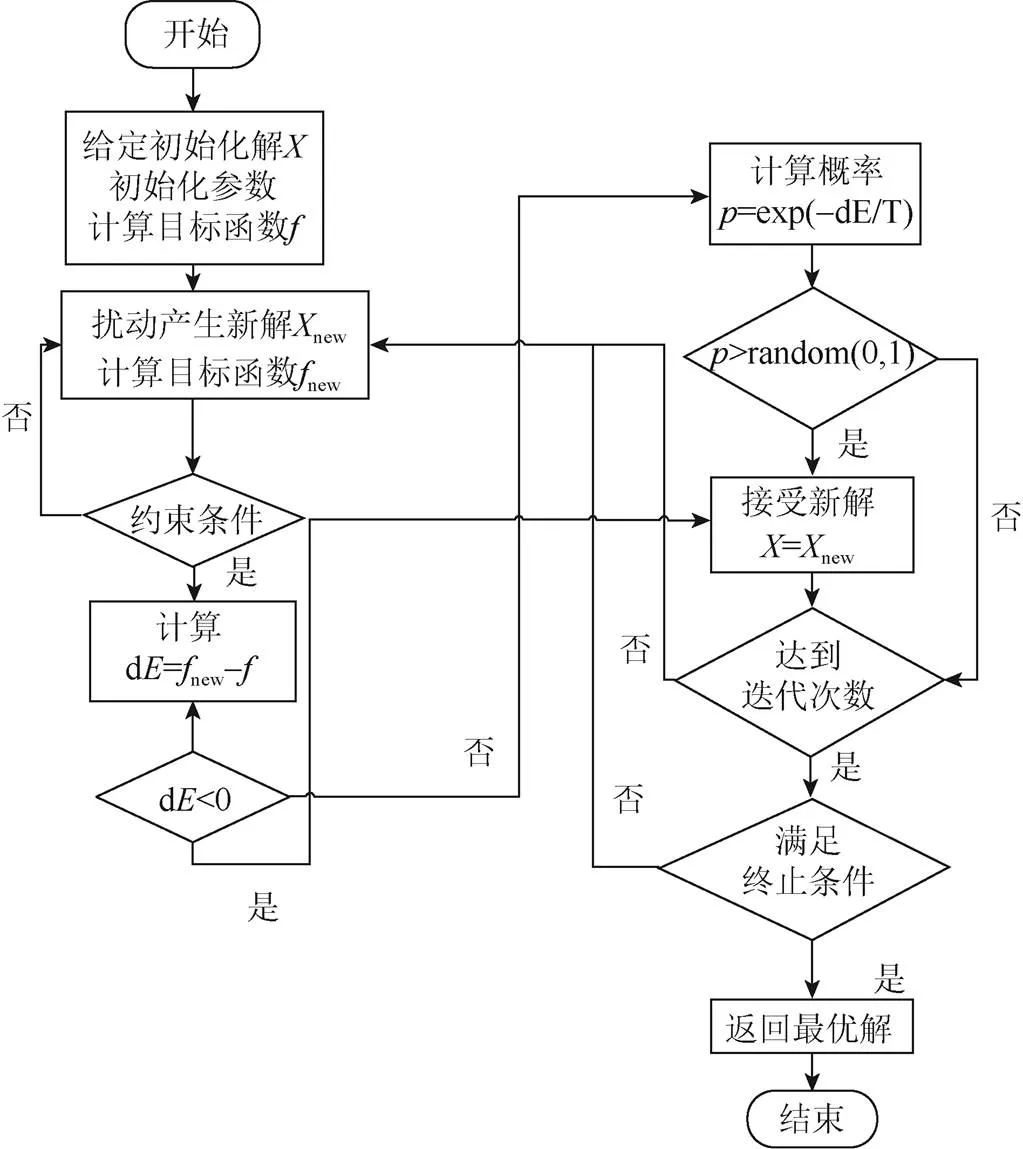
图2 模拟退火法流程图

3 算例分析

3.1 系统配置

以图1所示的多能流系统为例：包含如电制冷、吸收式制冷等能量转换设备和AA-CAES，用来满足输出侧的多种能源需求。在输入能源中，天然气的㶲系数为0.95[16]，低位热取值为50 MJ/kg[17]；压缩空气采用的给定压缩机效率为80%[18]，透平效率为85%的条件，采用㶲效率中值0.63，caes为0.63，负荷侧的冷热媒体温度分别为280.52 K和312.89 K。认为风力发电的预测足够准确，如图3和图4所示。以夏天和冬季的负荷需求为例，系统冷热电负荷如表1和表2所示[19]。

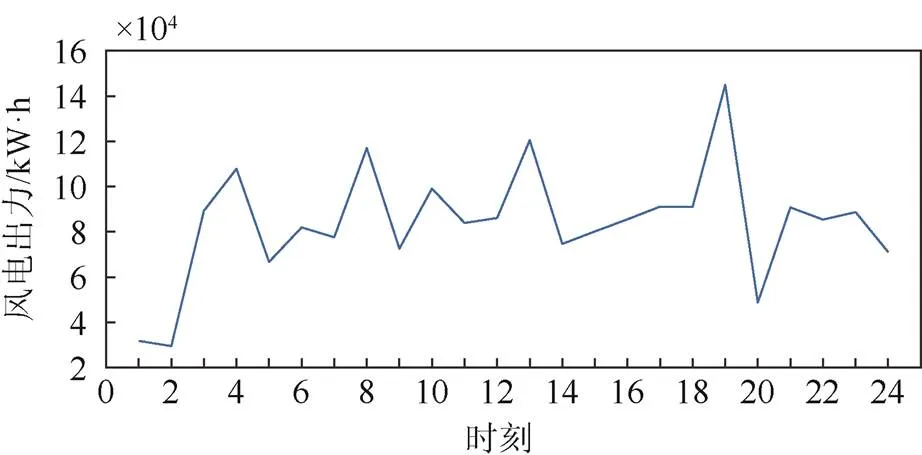
图3 夏季风电出力

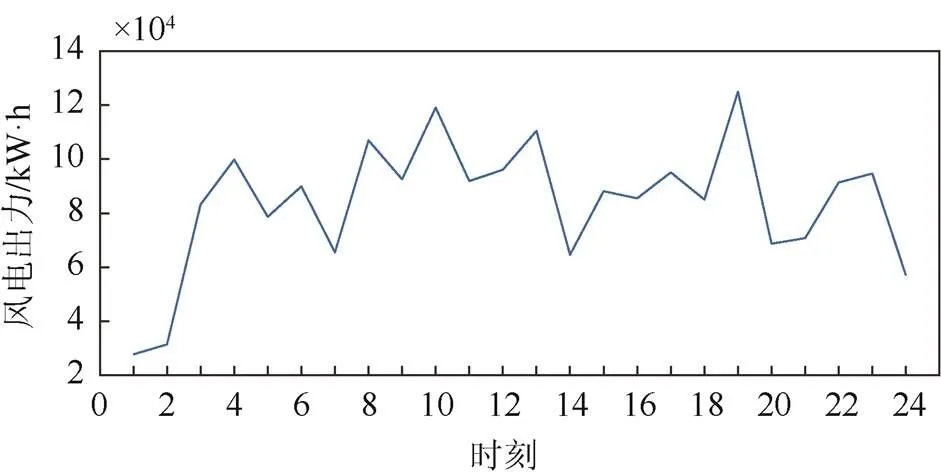
图4 冬季风电出力

3.2 模型求解与仿真分析

采用MATLAB进行仿真，使用模拟退火算法进行求解，在迭代过程中趋近最优解，迭代过程中以一定的概率接受非最优解以防止陷入局部最优。以1 h为时间尺度，求得1天内的系统最小㶲输入。图5和图6所示为系统冷能调度的数据，其中AC和EC分别为吸收式制冷和电制冷所产生冷能的数值。可以看到夏季吸收式制冷和电制冷产生一定数量的冷能，冬季则没有冷能产生。

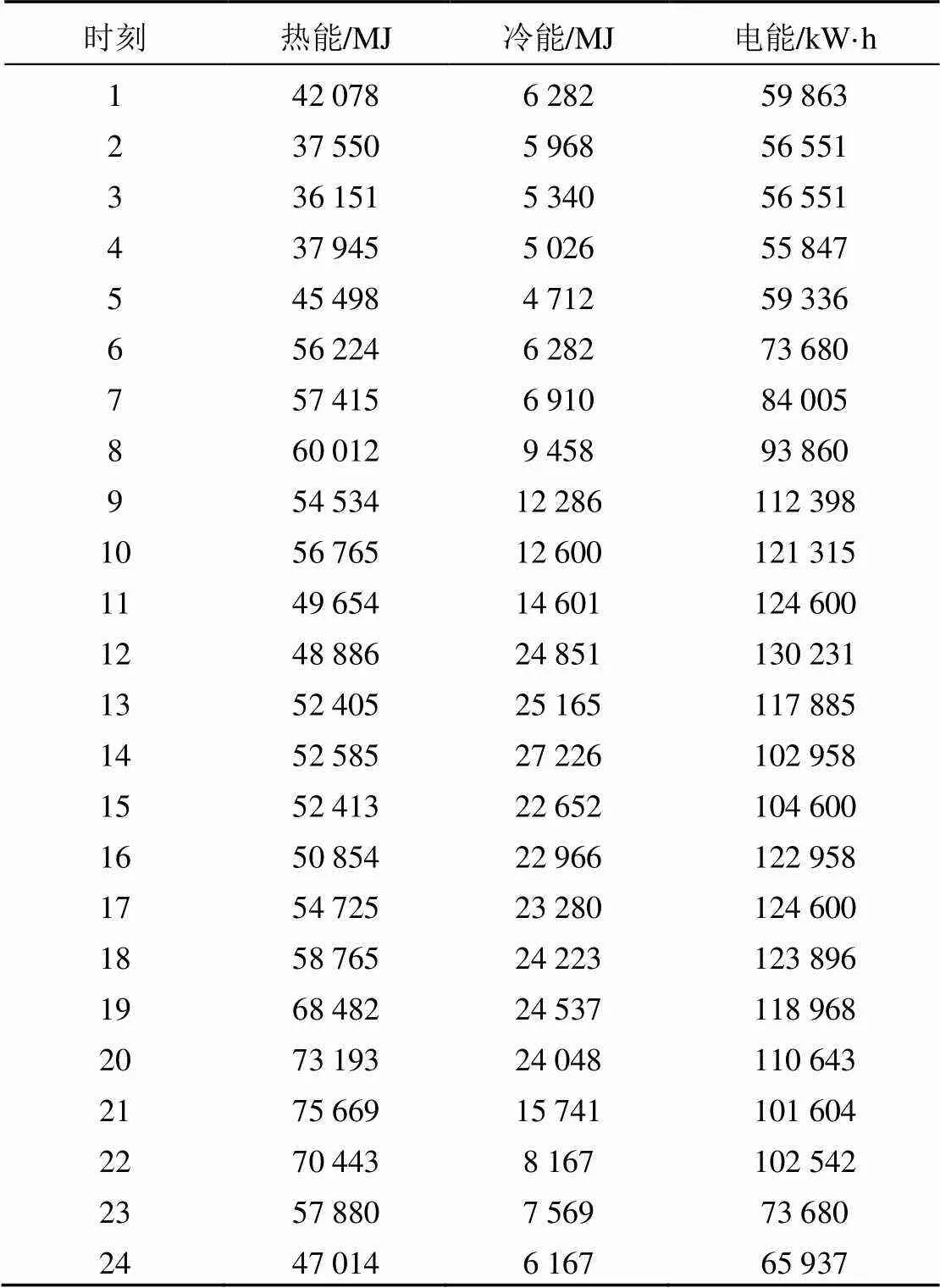
表1 夏季系统负载

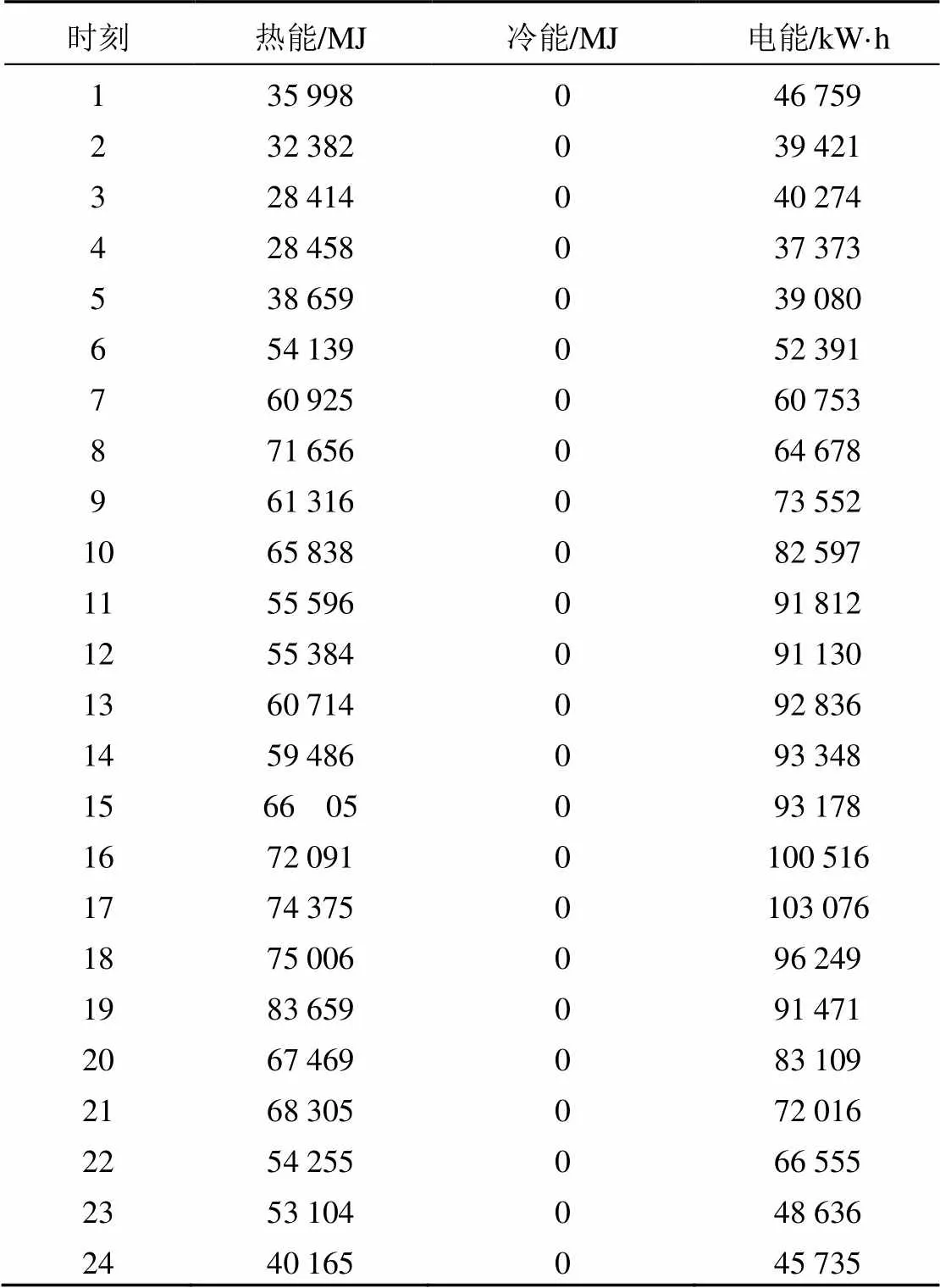
表2 冬季系统负载

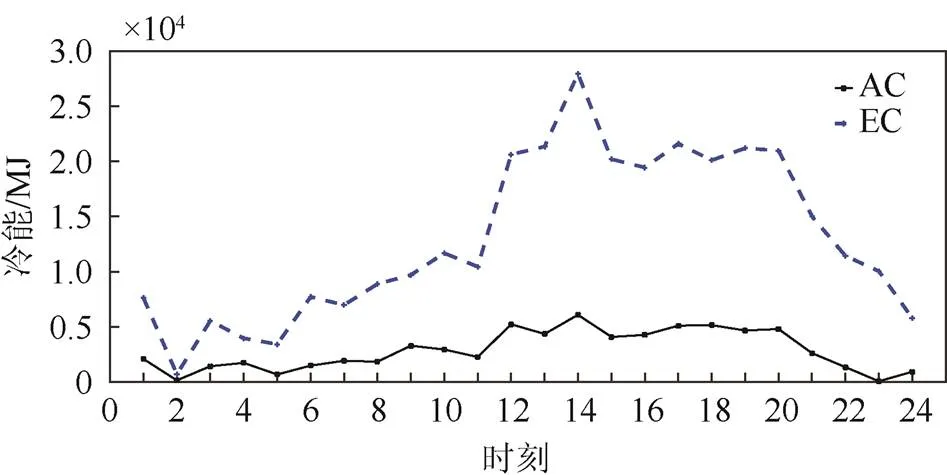
图5 夏季冷能调度结果

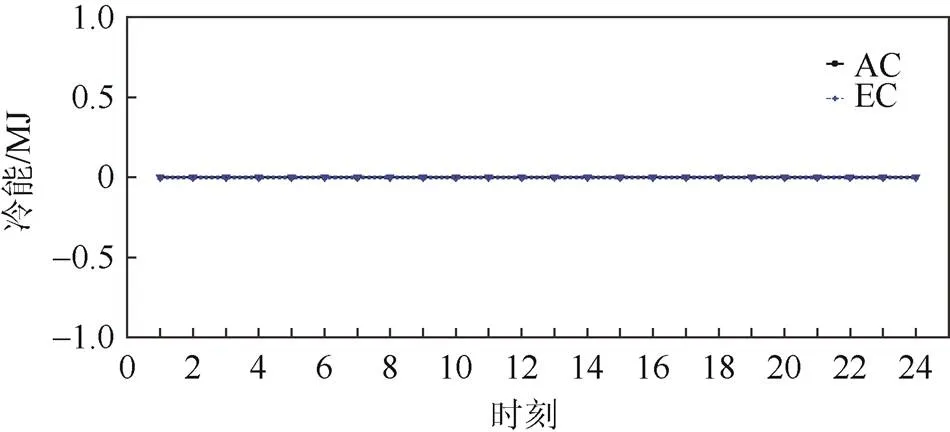
图6 冬季冷能调度结果

图7和图8所示为GB为燃气炉所产生热能，CHP为热电联产装置产生热能，CAES为压缩空气的储热装置输出热能，AC为吸收式制冷所消耗的热能。其中，在冬季，吸收式制冷不会消耗热量。

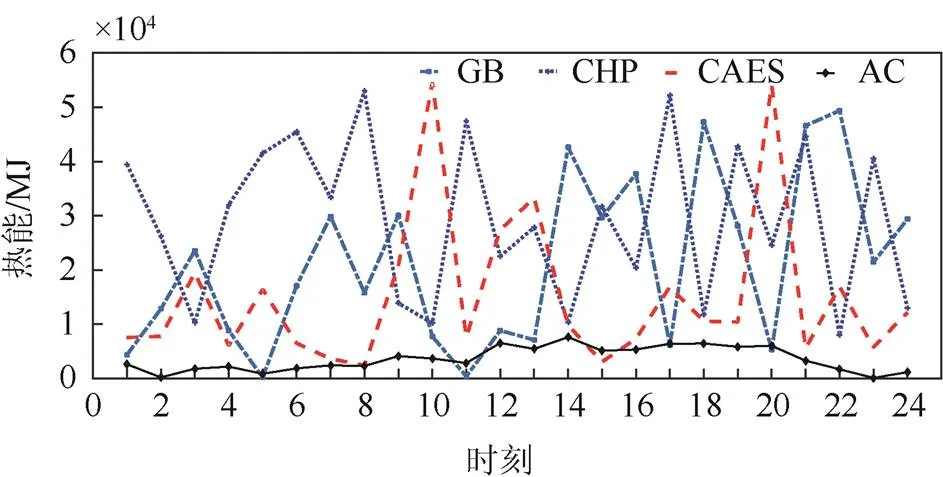
图7 夏季热能调度结果

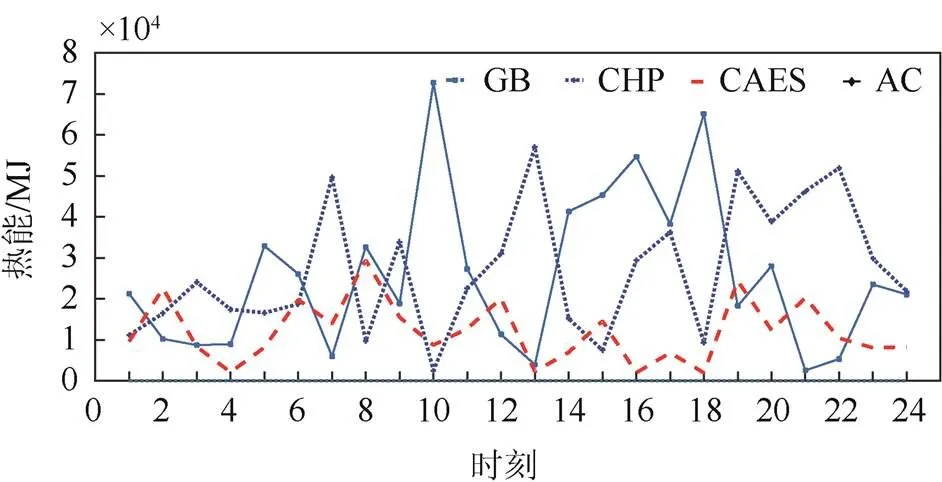
图8 冬季热能调度结果

图9和图10所示为CAES为压缩空气的发电功率，CHP为热电联产的发电功率，WIND为风力发电的电功率，EC为电制冷的耗电功率。可以看出，冬季的电制冷耗电量为0。

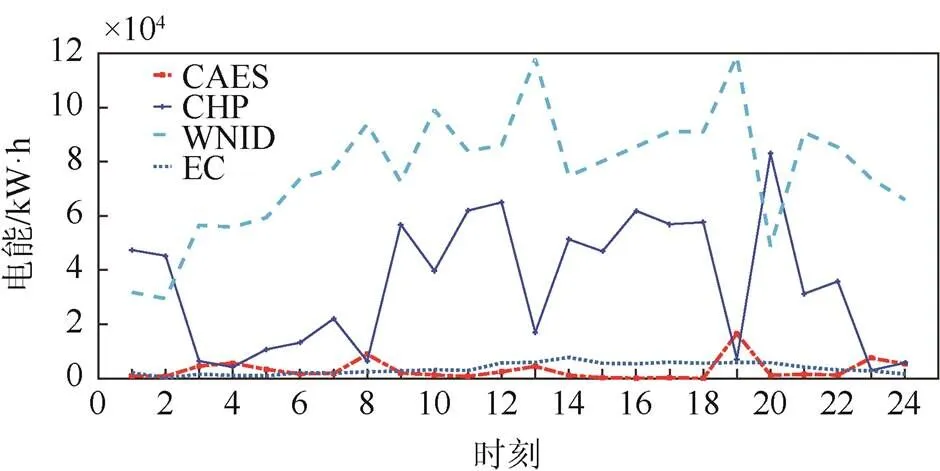
图9 夏季电能调度

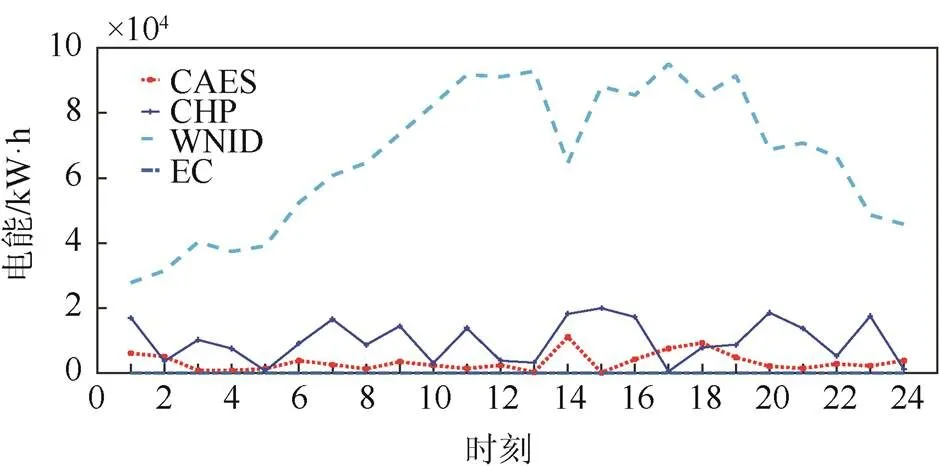
图10 冬季电能调度

图11和图12分别是夏季、冬季多能流调度的㶲输入值，24 h内以1 h为时间尺度，以系统㶲最小为目标的节能调度结果。从结果上可以看到，00:00—05:00系统的能源需求最低；06:00—10:00系统能源需求呈现明显上升趋势，并在10:00达到一个相对平稳的能源需求状态；10:00—20:00是系统能源需求最高的时间段，并在22:00开始系统能源需求急剧降低。这一现象也正好验证了本系统能源调度的合理性。并且，根据式（17）可求出本多能流系统㶲效率为38%～58%。

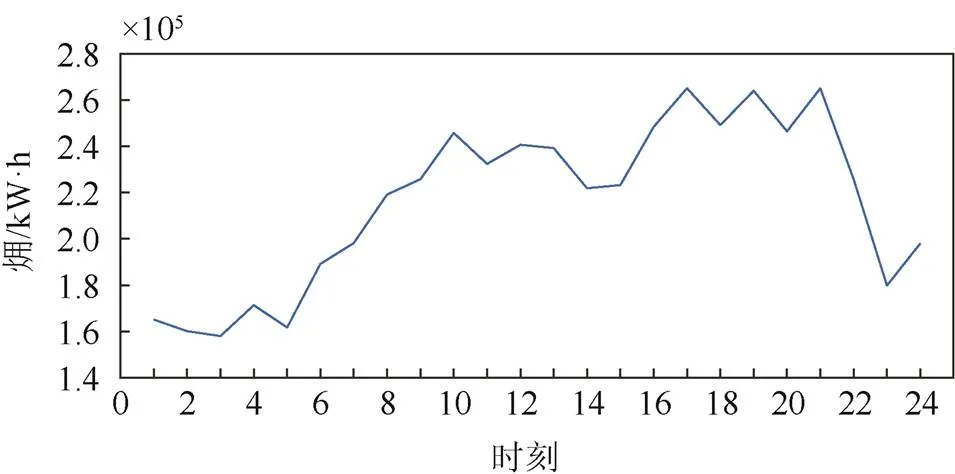
图11 夏季系统㶲输入

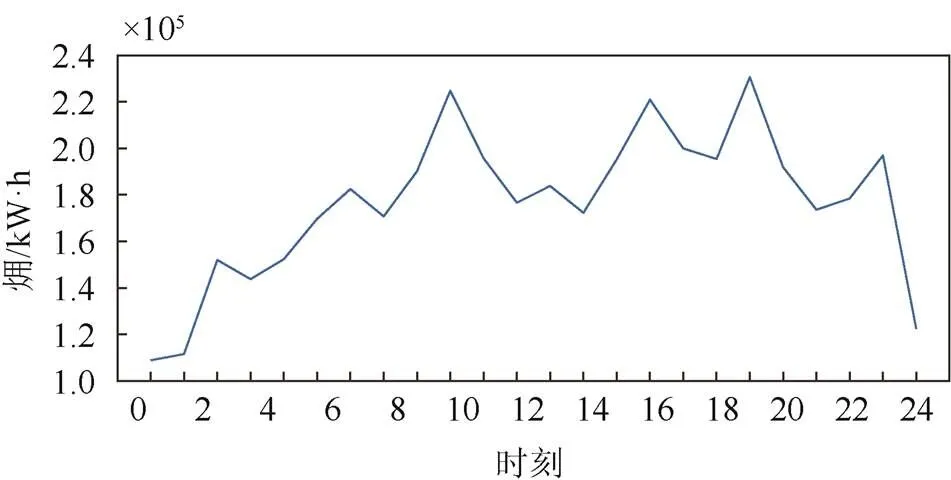
图12 冬季系统㶲输入

表3为AA-CAES对多能流系统㶲输入值的影响，㶲1列是本系统有压缩空气储能系统时的系统㶲输入，㶲2列是系统没有压缩空气储能系统时的㶲输入。从数据上可以看出，在有压缩空气平衡能量时，系统的㶲效率更高，节能性更好。在没有AA-CAES时，根据式（17）可以算出系统㶲效率为28%～47%。

表3 夏季不同情况对比

4 结论

本文首先将热力学第二定律的概念引入到多能流系统的能源调度中，基于㶲评估对多能流系统进行以最节能的目标的优化调度，建立以系统输入㶲最小的目标函数。在多能流系统中，采用AA-CAES作为储能系统，采用模拟退火算法对系统模型进行求解，求出系统最节能的能源调度方法：

（1）引入热力学第二定律的㶲概念评估系统的节能性，发展多能流系统最节能的调度方法，并且求出本多能流系统㶲效率为38%～58%。

（2）通过对夏季和冬季两个㶲能特点明显的季节性多能流系统进行节能调度，可以得出多能流系统的节能调度可行并且正确。

（3）通过是否使用AA-CAES的多能流系统㶲输入作对比研究，表明在具有压缩空气时，系统的节能性更好。

[1] 丁涛, 牟晨璐, 别朝红, 等. 能源互联网及其优化运行研究现状综述[J]. 中国电机工程学报, 2018, 38(15): 4318-4328.

DING TAO, MU CHENLU, BIE ZHAOHONG, et al. Review of energy internet and its operation[J]. Proceedings of the CSEE, 2018, 38(15): 4318-4328(in Chinese).

[2] 王永真, 张靖, 潘崇超, 等. 综合智慧能源多维绩效评价指标研究综述[J]. 全球能源互联网, 2021, 4(3): 207-225.

WANG YONGZHEN, ZHANG JING, PAN CHONGCHAO, et al. Multi-dimensional performance evaluation index review of integrated and intelligent energy[J]. Journal of Global Energy Interconnection, 2021, 4(3): 207-225(in Chinese).

[3] 孙宏斌, 郭庆来, 潘昭光. 多能流能量管理研究: 挑战与展望. 电力系统自动化, 2016, 40(15): 1-8.

SUN HONGBIN, GUO QINGLAI, PAN ZHAOGUANG. Energy management for multi-energy flow: challenges and prospects[J]. Automation of Electric Power Systems, 2016, 40(15): 1-8(in Chinese).

[4] 胡伟, 杨梓俊, 王瑾然, 等. 园区综合能源系统日前多目标优化调度[J]. 电力科学与技术学报, 2021, 36(1): 13-20.

HU WEI, YANG ZIJUN, WANG JINRAN, et al. Multi-objective optimal scheduling of integrated energy system in the industry park[J]. Journal of Electric Power Science and Technology, 2021, 36(1): 13-20(in Chinese).

[5] 黄秋立, 刘芸. 基于混合价格型需求响应的随机经济调度[J]. 电力科学与工程, 2020, 36(12): 30-36.

HUANG QIULI, LIU YUN. Stochastic economic dispatch considering hybrid price-driven demand response[J]. Electric Power Science and Engineering, 2020, 36(12): 30-36(in Chinese).

[6] 檀勤良, 丁毅宏. 考虑碳交易的火电节能调度优化模型及应对模式[J]. 电力自动化设备, 2018, 38(7): 175-181.

TAN QINLIANG, DING YIHONG. Optimal energy-saving dispatching model for thermal power considering carbon trading and its coping mode[J]. Electric Power Automation Equipment, 2018, 38(7): 175-181(in Chinese).

[7] 关欣, 黄素逸. 节能技术及案例分析[M]. 北京: 中国电力出版社, 2016.

[8] 吴晨曦, 陈泽昊, 张杰,等. 考虑先进绝热压缩空气储能的风力发电系统成本/供电可靠性评估[J]. 电力自动化设备, 2020, 40(2): 62-68.

WU CHENXI, CHEN ZEHAO, ZHANG JIE, et al. Cost/power supply reliability assessment of wind power generation system considering advanced adiabatic compressed air energy storage[J]. Electric Power Automation Equipment, 2020, 40(2): 62-68(in Chinese).

[9] 蔡杰, 张松岩, 杜治, 等. 含光热集热模块的先进绝热压缩空气储能系统容量配置策略[J]. 电力自动化设备, 2020, 40(7): 165-173.

CAI JIE, ZHANG SONGYAN, DU ZHI, et al. Capacity allocation strategy of advanced adiabatic compressed air energy storage system with solar thermal collector module[J]. Electric Power Automation Equipment, 2020, 40(7): 165-173(in Chinese).

[10] LUO X, WANG J H, KRUPKE C, et al. Modelling study, efficiency analysis and optimization of large-scale adiabatic compressed air energy storage systems with low-temperature thermal storage[J]. Applied Energy, 2016, 162: 589-600.

[11] 薛小代, 陈晓弢, 梅生伟, 等. 采用熔融盐蓄热的非补燃压缩空气储能发电系统性能[J]. 电工技术学报, 2016, 31(14): 11-20.

XUE XIAODAI, CHEN XIAOTAO, MEI SHENGWEI, et al. Performance of non-supplementary fired compressed air energy storage with molten salt heat storage[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 11-20(in Chinese).

[12] 李瑞, 陈来军, 梅生伟, 等. 先进绝热压缩空气储能变工况运行特性建模及风储协同分析[J]. 电力系统自动化, 2019, 43(11): 25-33.

LI RUI, CHEN LAIJUN, MEI SHENGWEI, et al. Modelling the off-design operation characteristics of advanced adiabatic compressed air energy storage and cooperative analysis of hybrid wind power and energy storage system[J]. Automation of Electric Power Systems, 2019, 43(11): 25-33(in Chinese).

[13] 韩中合, 庞永超. AA-CAES中蓄热系统模型改进与分析[J]. 太阳能学报, 2018, 39(6): 1566-1573.

HAN ZHONGHE, PANG YONGCHAO. Model modification and analysis of heat storage system in AA-CAES[J]. Acta Energiae Solaris Sinica, 2018, 39(6): 1566-1573(in Chinese).

[14] JIANG R, CAI Z, PENG K, et al. Thermo-economic analysis and multi-objective optimization of poly generation system based on advanced adiabatic compressed air energy storage system[J]. Energy Conversion and Management, 2021, 229: 113724.

[15] 郑亚锋, 魏振华, 高宇峰, 等. 多能流系统经济-节能多目标最优运行[J]. 电力系统及其自动化学报, 2020, 32(9): 77-85.

ZHENG YAFENG, WEI ZHENHUA, GAO YUFENG, et al. Multi-objective optimal operation of multi-energy carrier system considering economy and energy conservation[J]. Proceedings of the CSU-EPSA, 2020, 32(9): 77-85(in Chinese).

[16] 郭艳飞, 吴强, 程林, 等. 基于㶲效率的综合能源系统能效分析模型[J]. 可再生能源, 2017, 35(9): 1387-1394.

GUO YANFEI, WU QIANG, CHENG LIN, et al. Efficiency analysis model of integrated energy system based on the exergy efficiency[J]. Renewable Energy Resources, 2017, 35(9): 1387-1394(in Chinese).

[17] SHEHZAD M F, DAN M, MARIANI V, et al. A heuristic algorithm for combined heat and power system operation management[J]. Energies, 2021, 14(6): 1588.

[18] 徐玉杰, 陈海生, 刘佳, 等. 风光互补的压缩空气储能与发电一体化系统特性分析[J]. 中国电机工程学报, 2012, 32(20): 88-95.

XU YUJIE, CHEN HAISHENG, LIU JIA, et al. Performance analysis on an integrated system of compressed air energy storage and electricity production with wind-solar complementary method[J]. Proceedings of the CSEE, 2012, 32(20): 88-95(in Chinese).

[19] 代宪亚. 天然气冷热电联供能源系统运行优化研究[D]. 上海: 上海电力学院, 2017.

Energy-saving Scheduling of Multi-energy Flow Based on Exergy Evaluation

WU Chenxi, HE Zhanglu, YE Jianxiong, HONG Hanxiao

(School of Automation, Hangzhou Dianzi University, Hangzhou 310018, China)

Multi-energy flow system can realize the overall energy planning, multi-energy complementation and cascade utilization, and improve the energy utilization rate. In such a circumstance, a multi-energy flow system model of cooling, heating and power is established in this paper. Advanced adiabatic compressed air energy storage system (AA-CAES) is employed to balance the wind power and electrical power demand. Exergy analysis method of the second law of thermodynamics is used to evaluate the energy-saving index of the system to determine the most energy saving scheduling method for the multi-energy flow system. Taking typical wind power generation and cooling, heating and electricity demand of a park in winter and summer season as an example, simulated annealing arithmetic is adopted to carry out energy-saving scheduling of the system and exergy efficiency of the system is calculated. This paper makes a comparative study on the influence of advanced adiabatic compressed air on the energy-saving of the system. The results show that the system uses exergy efficiency to evaluate energy-saving index, and the efficiency is higher when the system has advanced adiabatic compressed air, which is about 38%～58%.

advanced adiabatic compressed air energy storage; exergy efficiency; wind power; multi-energy flow; simulated annealing arithmetic; energy-saving

10.3969/j.ISSN.1672-0792.2021.08.006

TM614;TK02

A

1672-0792(2021)08-0041-10

2021-05-10

国家自然科学基金（U1766201）；浙江省自然科学基金（LY20E070002）

吴晨曦（1978—），女，副教授，主要研究方向为新能源电力、多能流调度等；

何章露（1996—），男，硕士研究生，主要研究方向为新能源电力、多能流调度；

叶剑雄（1996—），男，硕士研究生，主要研究方向为新能源电力、多能流调度；

洪晗笑（1999—），女，硕士研究生，主要研究方向为新能源电力、多能流调度。