基于改进启发式算法的配电网随机潮流重构研究

邓鹏，刘敏，曹鹏，陈名扬

基于改进启发式算法的配电网随机潮流重构研究

邓鹏，刘敏，曹鹏，陈名扬

（贵州大学 电气工程学院，贵州 贵阳 550025）

配电网重构（distribution network reconfiguration，DNR）是确定配电网最优拓扑及减少网络损耗的有效措施。由于分布式电源（distributed generation，DG）和电动汽车（electric vehicle，EV）的大量接入导致了配电网潮流具有随机性，传统的重构方法已不能快速准确地得到随机潮流的重构最优解。提出一种考虑分布式电源和电动汽车的随机性和不确定性，以减少网络损耗和提高电压质量为目标的配电网重构模型，并采用启发式算法中的最优模式法（optimal power flow，OPF）和支路交换法（branch exchange method，BEM）加快重构速度。通过IEEE136测试系统验证该算法的有效性和正确性，结果表明：该算法实现了深度优化，能有效地解决随机潮流动态重构问题。

配电网重构；随机潮流；改进启发式算法；OPF；BEM

0 引言

电力行业的发展与其他各行业的发展紧密相关，可持续发展政策对电力行业的要求越来越高[1]。随着大量的分布式电源和电动汽车接入到电网中，分布式电源和电动汽车的不确定性和随机性会引起配电网潮流发生改变，从而导致配电网电压大幅波动和电压越限等问题[2]。配电网重构作为解决智能电网诸多问题的有效措施之一，越来越受关注。配电网重构可以高效利用可再生能源，实现双向潮流的灵活控制[3]。因此，对于含随机潮流的配电网重构方案的研究是智能电网首要解决的问题。

配电网重构是通过改变开关的状态获得最优拓扑，从而提高系统性能[4]。现有的重构方法包括数学优化算法[5]、进化算法[6]和启发式算法[7-8]。文献[5]提出了一种新颖的混合整数非线性规划模型，通过把混合整数非线性规划模型等效为两个线性化模型来提高收敛性，并采用增加约束条件的方法减少该算法的计算量。由于每个支路都有两种状态，随着支路的增加，解空间将会发生组合爆炸，因此不适用于大系统。文献[6]采用十进制对拓扑中的开关进行编码以减少编码空间，从而降低搜索空间并减少不可行解，同时采用无重复生成树的算法，生成进化算法的初始种群。但该算法只适用于小系统，在大系统中收敛慢，针对相同的运行方式可能会得到不同的结果。文献[7]对生成树法进行重构，在满足开关闭合规则的前提下，大幅度降低生成树数量。最优流模式收敛性好，不足是速度慢、全局最优解搜索困难。文献[8]提出了基于灵敏分析的支路交换法，通过分析值确定配电网变换前后潮流状态，得出最佳拓扑结构。支路交换法虽可增加可行解，但却降低了收敛速度且增加全局最优解搜索难度。

考虑分布式电源和电动汽车加入配电网时，重构必须要解决非线性交流潮流计算和网络辐射状运行这两个复杂问题[9]。本文主要是考虑配电网如何进行辐射状运行的问题。现有确保配电网辐射状运行的主要方案有：基于回路[10]、基于路径[11]和基于节点[12-13]这3种方法，前两种方案主要是采用进化算法。基于节点的一个方案是生成树方法[12]，主要思想是网络中除电源节点外其他的节点只有一个父节点；另一个方案[13]是依据辐射状拓扑中支路数比节点数少一个，并且每个节点到电源节点的路径都是连通的。基于节点的方案主要是采用数学优化算法和启发式算法[14]。由于数学优化算法无法应用于大系统，故通常采用启发式算法，启发式算法主要包括最优流模式法和支路交换法，但仅仅使用其中一种方法不能快速得到最优解。

因此，为了提高随机潮流重构的快速性，本文结合启发式算法中最优流模式法和支路交换法这两种方案，提出了一种基于改进启发式算法的配电网随机潮流重构方法。该方法包括3个步骤：首先，从网络中的封闭环路开始，依次打开开关，直到所有的环路都打开并获得辐射状拓扑；然后，分别用第二步和第三步对第一步所得的初始拓扑进行修正，进一步得到更好的拓扑结构。采用IEEE136大型测试系统来验证该方法的有效性和正确性；最后，和其他启发式算法进行对比以验证其快速性和准确性。

1 不确定性参量建模

对不确定性参量进行建模，基本模型包括风力发电功率模型、光伏发电功率模型和电动汽车充电功率不确定性模型。

1.1 DG发电功率不确定性

由于分布式电源（distributed generation，DG）发电功率受风速和光照强度的影响较大，在建模时不能将DG的出力功率简单看成恒定的某一类节点。经大量研究数据可知，风速的变化最接近Weibull概率分布模型[15]，因此可以用该模型对风力发电出力进行预测，其公式如下：

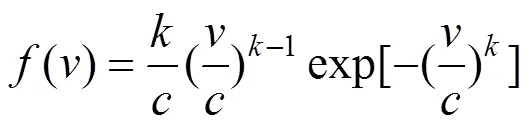
式中：()为风速概率；表示风速；为形状参数；为尺度参数。再由风速和发电功率之间的关系可以得到出力功率，具体如下：

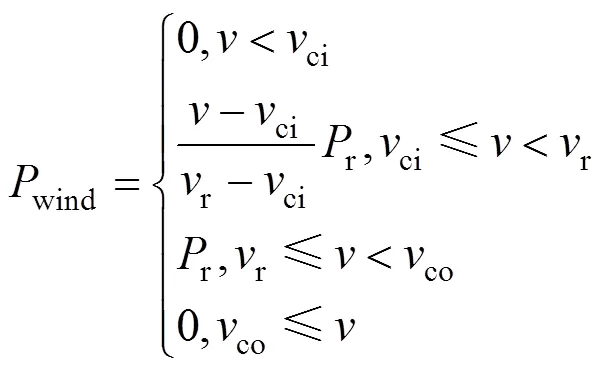
式中：ci为切入风速；r为额定风速；co为切出功率；wind为风力发电的输出功率；r为风力发电最大额定功率。

光照强度是影响光伏发电的主要因素，目前主要是用Beta分布对其不确定性进行建模[15]，因此光伏发电功率预测如下：

式中：()表示光照强度概率；为光照强度；、表示Beta分布的参数；为伽马函数。

通过下式可以得出光伏发电出力功率：

式中：pv为光伏发电输出功率；A为第块光伏板面积；η为光电转换效率。

1.2 EV负荷不确定性

影响EV负荷特性不确定性的主要有汽车行驶路程、充电起始时刻和充电时长3个因素[16]，经研究表明，汽车行驶路程和充电起始时刻都是近似服从正态分布函数，充电时长与行驶路程呈线性关系。汽车行驶路程：

式中：()表示行驶路程概率；为行驶路程；δ表示行驶路程的期望值；μ表示行驶路程的标准差。

充电起始时刻：

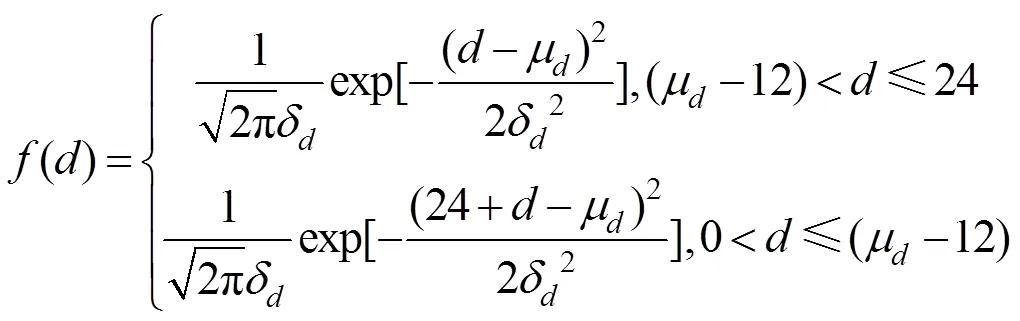
式中：()表示充电起始时刻概率；为充电起始时刻；δ表示行驶路程的期望值；μ表示行驶路程的标准差。

充电时长：

式中：为充电时长；每百km耗油量；c为恒定充电功率；充电效率。

电动汽车电池的初始值：

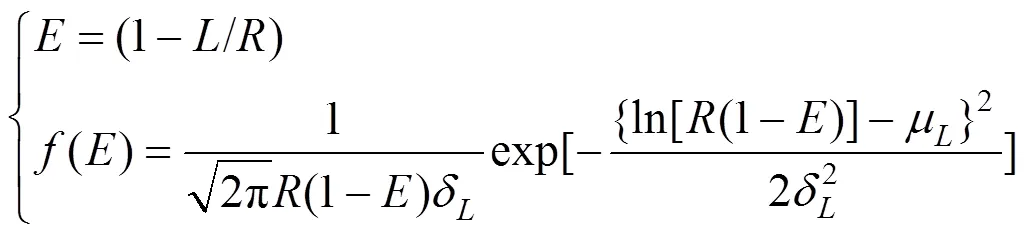
式中：()表示电池初始值的概率；为电动汽车电池的初始值；为充满电时的行驶路程。由此可以得到电动汽车(>)时刻的功率需求期望值，即：

式中：为电动汽车的数量；()为时刻单台电动汽车充电的有功功率，则：

2 随机配电网重构模型

2.1 目标函数

本文从配电网运行的经济角度考虑，以配电网运行的损耗最低建立如下目标函数：

2.2 约束条件

（1）有功功率约束

设有功功率约束为：

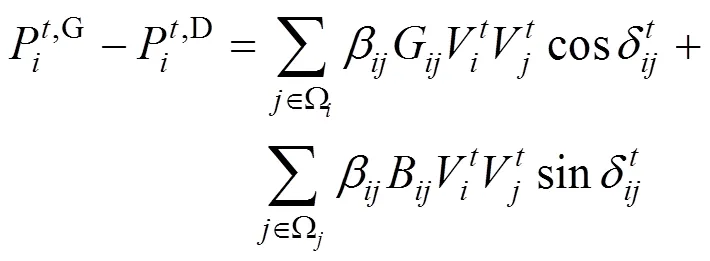
（2）无功功率约束

设无功功率约束为：

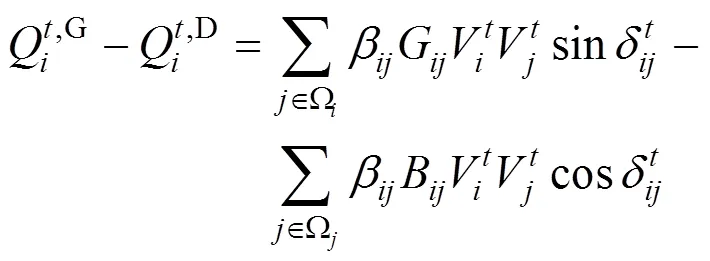
（3）支路最大容量约束

设支路最大容量为：

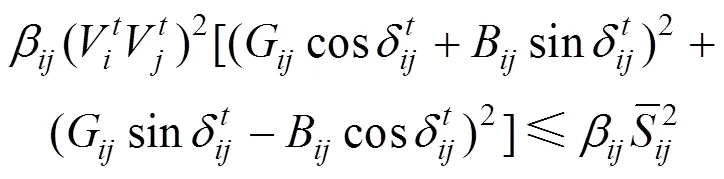
（4）节点电压约束

设节点电压为：

（5）分布式发电输出有功功率约束

设分布式发电输出有功功率为：

（6）分布式发电输出无功功率约束

设分布式发电输出无功功率为：

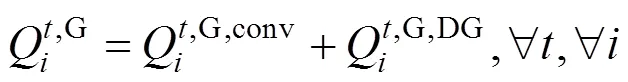
2.3 辐射状和连通性处理

根据图论中网络辐射状的必要条件为节点数等于支路数加1，可用式（18）判断网络是否为辐射状。

式中：b为节点数；l为支路数。

连通性可以根据节点到电源节点之间的距离来判断。当联通时，该距离有限，即：

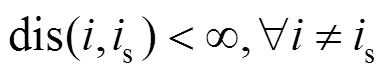
3 改进启发式重构方法

改进启发式重构方法分为3个阶段，即最优流模式法、支路交换法和基于第二类开关支路交换法。其中第二阶段和第三阶段是在第一阶段基础上进行的，第三阶段是对第二阶段的完善补充。下面将分别介绍各部分的详细流程，在执行改进启发式重构方法之前，关闭网络中的每一个开关，使网络具有环路。

3.1 最优流模式法

最优流模式法[1]是在不形成孤岛的情况下打开环路，其迭代次数等于初始网络环路中的环路数，每次迭代选择并打开一个位于环路内的联络开关，遍历环路中的每一个开关，并打开对应损耗最小的分段开关，直到获得辐射状的初始拓扑。

第一阶段的详细流程如下：

步骤a：获取系统的电源、负载和拓扑信息，并找到回路中的所有开关。

步骤b：打开环路中的一个开关，然后通过式（19）检查系统的连通性。如果每个节点与电源节点都是连通的，则求解网损值保存在1中；否则，给目标值赋一个较大的正数将其保存在1中，关闭开关。

步骤c：重复步骤a、b，至到遍历环路中所有开关。

步骤d：根据步骤b和c找到环路1中最小的目标函数，并打开相对应的开关。

步骤e：重复步骤b～d至满足式（18），此时得到的拓扑为辐射状。

在第一阶段中获得的拓扑即为初始拓扑，第二阶段和第三阶段都将在初始拓扑的基础上进行。

步骤b是对固定网络拓扑求解静态重构等效于每个时段的每种场景下的随机潮流，静态重构费时少。但是，在第一阶段中获得的初始拓扑并不接近最佳拓扑（之间的相对误差高达5%）。为了在第一阶段中获得的初始拓扑基础上得到更准确的拓扑结构，将采用第二阶段对初始拓扑进行优化。

3.2 支路交换法

由于每条支路只含有一个分段开关或联络开关，根据式（18）辐射状拓扑中支路数量比节点数少一个。由此可以把初始拓扑用一组开关来表示，以下操作都是针对开关进行。

3.2.1 排除初始拓扑中的部分开关

第二阶段首先将初始拓扑中的分段开关更换为联络开关，并执行第一阶段得到不同的拓扑，然后从不同拓扑中找到最佳的拓扑。但是，第二阶段中需要执行第一阶段的次数由初始拓扑中分段开关的个数决定；因此，如果系统中的节点数越大，执行第二阶段花费的时间越长。考虑到排除一部分容易确定状态的分段开关可以减少第二阶段的耗时。因此，下面给出了排除开关的原因并对其进行分类。

第一类：在形成辐射状拓扑的过程中，必须保证电源节点与各节点之间的连通性，电源附近的开关一般都是闭合的，即不需要更换电源附近的开关状态。其距离电源的位置可以通过设置参数1来控制。

第二类：为了在结束节点附近不产生孤岛现象，结束节点上游的分段开关也需要闭合，即不需要更换结束节点附近的开关状态，其距离结束节点的位置通过设置参数2来控制。

第三类：不属于任何环路的分段开关，也需要闭合，即容易确定其开闭状态。

3.2.2 第二阶段的详细流程

第二阶段的详细流程如下：

步骤a：初始拓扑中的所有分段开关用集合2来表示。

步骤b：把第一类、第二类和第三类开关从集合2中排除。

步骤c：将2中的分段开关强制更改为联络开关，并关闭所有其他开关。然后执行第一阶段以获取辐射状拓扑结构，通过式（11）计算目标函数，保存该拓扑所对应的损耗值。

步骤d：将联络开关关闭，切换回分段开关。

步骤e：对2中的每个开关重复步骤c～d，最终得到不同的拓扑。

在第二阶段中获得的每个辐射状拓扑都将作为第三阶段的输入。

3.3 基于第二类开关支路交换法

在第二阶段中，假设了第二类开关的状态不变；第三阶段作为第二阶段的补充，考虑了初始拓扑中第二类开关的状态，在第三阶段中对第二类开关进行更换可以减少耗时。即通过第二阶段和第三阶段就可以遍历除第一和三类之外的所有分段开关。在第三阶段中，主要是通过打开一个第二类的分段开关并关闭另一个联络开关来更改结束节点附近开关的状态。当闭合的开关断开时，为确保网络的连通性，只需要把断开开关中的下游节点连接到网络中的其他节点上。

第三阶段的详细流程如下：

步骤a：根据第二阶段中得到的拓扑，设3为仅包括所有第二类开关的集合。

步骤b：在不改变拓扑的辐射性和连通性的情况下，把3中的分段开关更换成联络开关并关闭一个联络开关，保存新形成的拓扑在集合中。

步骤c：重复步骤“3.2支路交换法”找到集合，对中的每个元素按式（11）求解，然后记录目标函数，并找出能减少目标函数的开闭开关组合操作。

步骤d：对3中的不同开关重复步骤b～c。

步骤e：组合中任意两个或多个使得目标函数减少的开关动作，并重复步骤b～d。

步骤f：对于第一阶段和第三阶段中获得的不同辐射状拓扑结构，重复步骤a～e。

4 算例仿真

为验证本文所提方法的正确性和有效性，通过夏季典型日以每小时进行重构，考虑到风电、光伏发电和充电汽车不确定性的影响，并分析每一次重构消耗时间得出该方法的快速性，该仿真在IEEE136测试系统[17]上进行，测试系统包括136个节点和135条支路，由135个分段开关和21个联络开关组成，其基准电压为13.8 kV，基准功率为10 MVA，总负荷为45.288+i48.008 MVA，系统闭合时其总的损耗为271.85 kW。风电光伏发电和电动汽车负荷选取夏季典型代表日，具体数据参考文献[16]和[17]。分别在89、107、135节点处加入相同型号的风电发电WT1、WT2、WT3，在96、15、52节点处加入相同型号的光伏发电PV1、PV2、PV3，在132、25、83节点处接入相同型号的电动汽车群EV1、EV2、EV3。本文算法涉及到的参数为：=1.75，=5.92，ci=4 m/s，r=14 m/s，co=24 m/s，r=1 MV，1=4，2=5，光伏发电机组共50×20组，A=2.16 m2，η=13.44%，=0.49，=5.13；电动汽车100辆为一组，=15 kW，c=3.6 kW。图1为初始拓扑辐射状接线，其网络损耗为295.97 kW。

图1 改进的IEEE136测试系统网络结构

通过模型公式和相关的计算，得到了风电、光伏和电动汽车负荷一天中每个小时的功率和负荷出力期望值，如图2所示。为了验证所提方法每一步的有效性，分别用所提方法的第一阶段（方法1）、第一阶段和第二阶段（方法2）、第一阶段和第三阶段（方法3）、以及第一～三阶段（方法4）进行对比重构，通过MATLAB仿真平台对IEEE136测试系统进行仿真验证，其重构结果如表1所示。

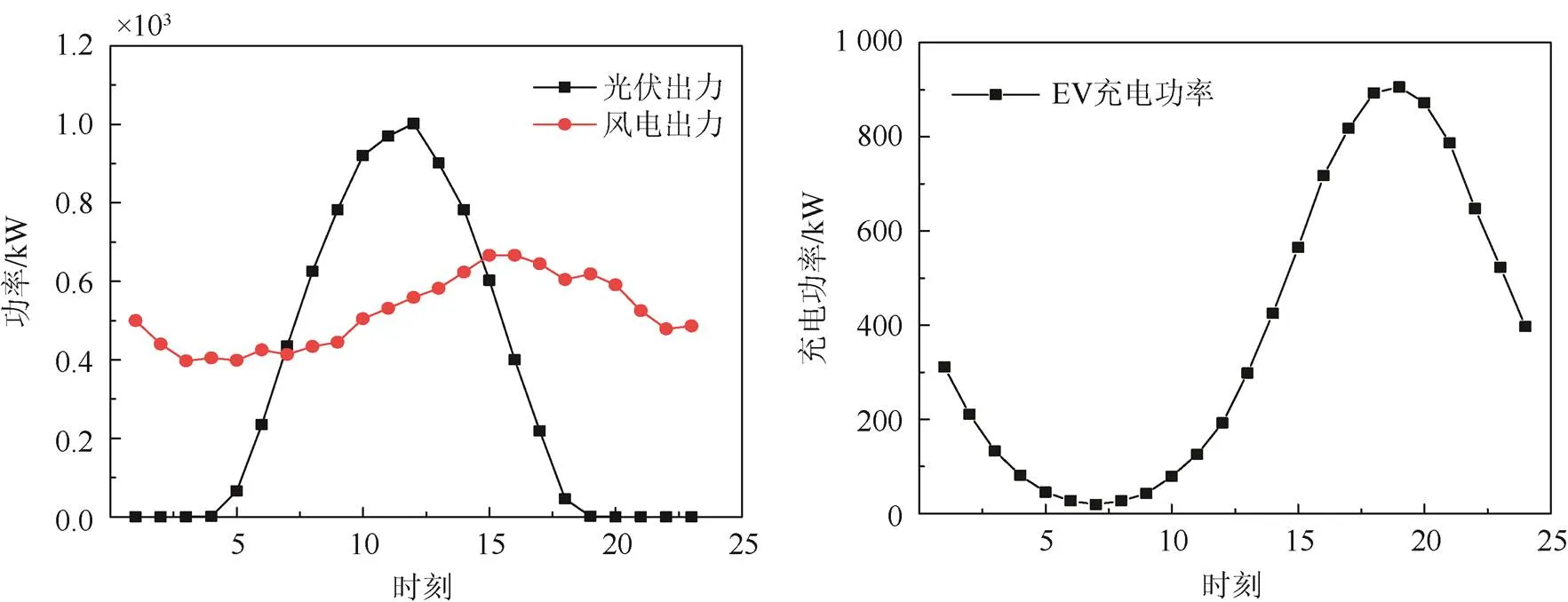
图2 风电光伏功率和电动汽车负荷曲线

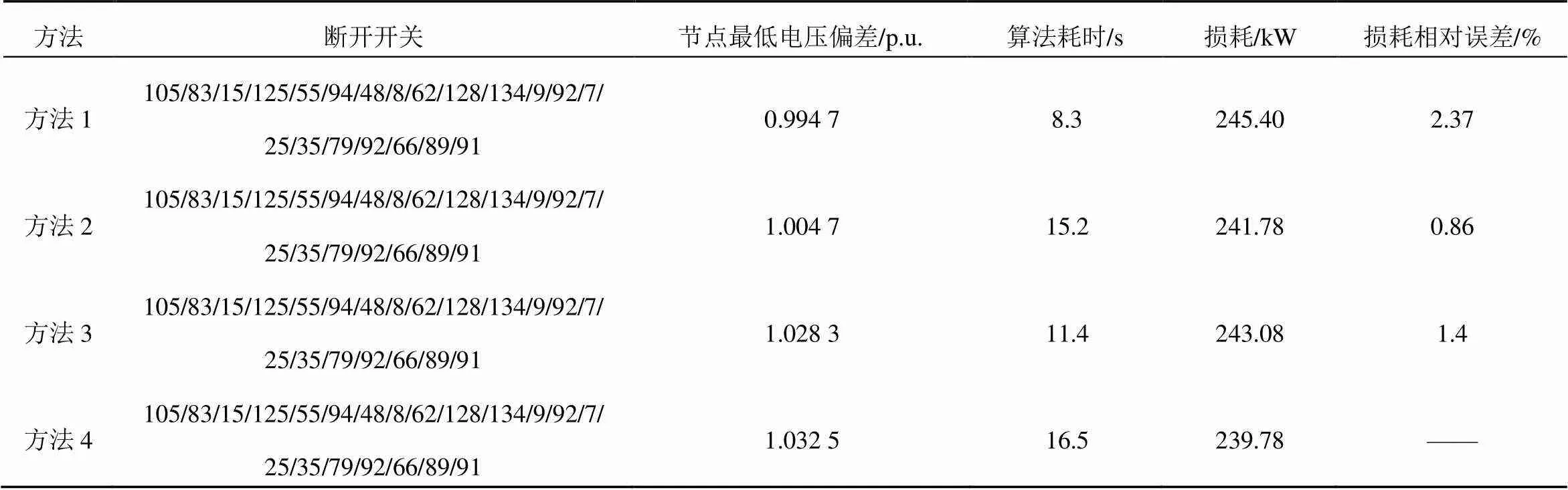
表1 12点时4种不同步骤重构的结果

表1显示了4种方法的仿真结果，分别以断开开关、算法耗时、功率损耗、节点最低电压偏差和损耗相对误差为比较指标，对所提方法的每一阶段进行评价分析。由表1可以看出，每种算法都可以得到重构最优解，仅有第一阶段参加重构时，算法耗时最小为8.3 s。对比方法2和3可知，第三阶段比第二阶段耗时少3.8 s，由此可以说明把第二类开关放到第三阶段中处理可以提高重构速度；以方法4重构结果为基准，得出每种方法的损耗相对误差。由表1的最后一栏可以看出，在第一阶段的基础上，加入第二阶段比第三阶段减少的损耗多0.54%，即在第一阶段所得初始拓扑的基础上，运用第二阶段和第三阶段都可以提高初始拓扑的准确性，而第二阶段得到的拓扑更为精确。

图3和表1中第3列说明了该算法可以提高节点最低电压。由于节点电压主要受第二类分段开关的影响较大，方法3比方法2提高的电压偏差多0.023 6；1.05为电压越界上限。由图3可以看出，在26、27、56节点和87到120节点处的越界节点电压较多，而方法4较其他方法显著地降低了越界的电压，使各个节点处的电压曲线平稳，从而提高了电压质量。方法4重构所得的各项指标中，耗时16.5 s相对较多，但这个耗时在实际工程中可以接受，因此方法4更具有实用性。

图3 12点时系统中各个节点处的电压分布图

表2是本文方法与文献[18]方法对比情况，开关动作只有3个不同，损耗较低，精度较高，最低节点电压明显提高，重构速度提高了45.5倍，其原因为配电网中每条支路的初始状态设置为关闭，并且网络中存在环路。为了实现放射状网络，需要改变一些常闭的分段开关作为联络开关。文献[18]是以不同维度进行同时优化所有开关，即在一次迭代中需要同时改变所有开关的状态，对于大型系统的重构这会非常耗时。相反，最优流模式法和支路交换法的第一阶段使用最优流模式法来确定重构方案的不同维度，即只有一个开关可以在一次迭代中更改其状态。因此，本文方法可以有效地提高网络重构的效率。

表2 不同方法对比

5 结论

由于分布式电源和电动汽车的大量接入，配电网的潮流已经由单向变为随机潮流。本文针对随机潮流的配电网重构，提出了一种精确且快速的改进启发式重构算法，该算法包括3个阶段：第一阶段是通过打开环路获得辐射状的初始拓扑；为了提高拓扑精度，第二阶段通过强制打开初始拓扑中的分段开关以获得更精准的拓扑；第三阶段在第一阶段和第二阶段的基础上，采用支路交换法控制第二类型分段开关的动作，从而加快重构的速度。第二阶段和第三阶段分别对重构的精度和速度进行了改进，并通过仿真与其他启发式算法对比，验证了该方法的准确性和快速性。该方法还可以应用于微电网的规划、重构等领域。

[1] 谭文勇, 刘敏, 罗永平, 等. 配电网动态重构算法及时段划分研究综述[J]. 电测与仪表, 2020, 57(11): 63-67.

TAN WENYONG, LIU MIN, LUO YONGPING, et al. Review of research on algorithm and time division of dynamic reconfiguration of distribution network[J]. Electrical Measurement and Instrumentation, 2020, 57(11): 63-67(in Chinese).

[2] 葛少云, 张有为, 刘洪, 等. 考虑网架动态重构的主动配电网双层扩展规划[J]. 电网技术, 2018, 42(5): 1526-1533.

GE SHAOYUN, ZHANG YOUWEI, LIU HONG, et al. Bi-layer expansion programming method for active distribution network considering dynamic grid reconfiguration[J]. Power System Technology, 2018, 42(5): 1526-1533(in Chinese).

[3] 潘本仁, 王和春, 张妍, 等. 含分布式电源的主动配电网重构策略研究[J]. 电力系统保护与控制, 2020, 48(15): 102-107.

PAN BENREN, WANG HECHUN, ZHANG YAN, et al. Study on an active distribution network reconstruction strategy with distributed power supply[J]. Power System Protection and Control, 2020, 48(15): 102-107(in Chinese).

[4] 李扬, 韦钢, 马钰, 等. 含电动汽车和分布式电源的主动配电网动态重构[J]. 电力系统自动化, 2018, 42(5): 102-110.

LI YANG, WEI GANG, MA YU, et al. Dynamic reconfiguration of active distribution network considering electric vehicles and distributed generations[J]. Automation of Electric Power Systems, 2018, 42(5): 102-110(in Chinese).

[5] BORGES M C O, FRANCO J F, RIDER M J. Optimal reconfiguration of electrical distribution systems using mathematical programming[J]. Journal of Control, Automation & Electrical Systems, 2014, 25: 103-111(in Chinese).

[6] 阳晓明, 吕红芳, 朱辉. 基于改进人工鱼群算法的配电网络重构[J]. 电测与仪表, 2020, 57(17): 72-78.

YANG XIAOMING, LV HONGFANG, ZHU HUI. Reconfiguration of distribution network based on improved artificial fish swarm algorithm[J]. Electrical Measurement & Instrumentation, 2020, 57(17): 72-78(in Chinese).

[7] 王威, 韩学山, 王勇, 等. 一种减少生成树数量的配电网最优重构算法[J]. 中国电机工程学报, 2008, 28(16): 34-38.

WANG WEI, HAN XUESHAN, WANG YONG, et al. A distribution network optimal reconfiguration algorithm of reducing the number of spinning trees[J]. Proceedings of the CSEE, 2008, 28(16): 34-38(in Chinese).

[8] GONZALEZ A, ECHAVARREN F M, ROUCO L, et al. A sensitivities computation method for reconfiguration of radial networks[J]. IEEE Transactions on Power Systems, 2012, 27(3): 1294-1301.

[9] ZHAN J, LIU W, CHUNG C Y, et al. Switch opening and exchange method for stochastic distribution network reconfiguration[J]. IEEE Transactions on Smart Grid, 2020, 11(4): 2995-3007.

[10] ASRARI A, WU T, LOTFIFARD S. The impacts of distributed energy sources on distribution network reconfiguration[J]. IEEE Transactions on Energy Conversion, 2016, 31(2): 606-613.

[11] RAMOS E R, EXPOSITO A G, SANTOS J R, et al. Path-based distribution network modeling: application to reconfiguration for loss reduction[J]. IEEE transactions on power systems, 2005, 20(2): 556-564.

[12] LAVORATO M, FRANCO J F, RIDER M J, et al. Imposing radiality constraints in distribution system optimization problems[J]. IEEE Transactions on Power Systems, 2012, 27(1): 172-180.

[13] FRANCO J F, RIDER M J, LAVORATO M, et al. A mixed-integer LP model for the reconfiguration of radial electric distribution systems considering distributed generation[J]. Electric Power Systems Research, 2013, 97(4): 51-60.

[14] MISHRA S, DAS D, PAUL S. A comprehensive review on power distribution network reconfiguration[J]. Energy Systems, 2017, 8(2): 227-284.

[15] 谢琳宇, 唐忠, 黄星宇, 等. 考虑分布式电源和电动汽车不确定性的双层动态配网重构[J]. 电力系统保护与控制, 2020, 48(10): 1-11.

XIE LINYU, TANG ZHONG, HUANG XINGYU, et al. Bi-layer dynamic reconfiguration of a distribution network considering the uncertainty of distributed generation and electric vehicles[J]. Power System Protection and Control, 2020, 48(10): 1-11(in Chinese).

[16] 闫红强. 含分布式电源及电动汽车充电负荷电力系统的概率潮流计算方法研究[D]. 兰州: 兰州理工大学, 2017.

[17] AHMADI H, MARTÍ J R. Minimum-loss network reconfiguration: a minimum spanning tree problem[J]. Sustainable Energy, Grids and Networks, 2015, 1: 1-9.

[18] UNESP-FEIS electrical energy systems planning laboratory homepage[EB/OL]. [2021-04-02]. http:// www.dee.feis.unesp.br/lapsee/.

Research on Probabilistic Power Flow Reconfiguration of Distribution Network Based on Improved Heuristic Algorithm

DENG Peng, LIU Min, CAO Peng, CHEN Mingyang

(The Electrical Engineering College, Guizhou University, Guiyang 550025, China)

Distribution Network Reconfiguration (DNR) is an effective measure to determine the optimal topology of the distribution network and reduce network losses. Due to the massive access of distributed generation (DG) and electric vehicles (EV), the power flow of the distribution network is probabilistic. The traditional reconstruction method can no longer quickly and accurately obtain the reconstruction optimal solution of probabilistic power flow. Proposes a reconstruction model that considers the randomness and uncertainty of distributed generation and electric vehicles, aims to reduce network losses and improve voltage quality, and adopts optimal power flow (OPF) and branch exchange method (BEM) in the heuristic algorithm to speed up reconstruction. The validity and correctness of the algorithm are verified by the IEEE136 test system. The results show that this algorithm achieves deep optimization and can effectively solve the problem of dynamic reconstruction of probabilistic power flow.

distribution network reconfiguration; probabilistic power flow; improved heuristic algorithm; OPF; BEM

10.3969/j.ISSN.1672-0792.2021.08.005

TM721

A

1672-0792(2021)08-0033-08

2021-01-29

邓 鹏（1992—），男，硕士研究生，研究方向为电力系统及其自动化；

刘 敏（1972—)，女，教授，主要研究方向为电力系统分析、电力市场、电力系统优化；

曹 鹏（1997—），男，硕士研究生，研究方向为电力投资规划、电力市场；

陈名扬（1995—），男，硕士研究生，研究方向为电网优化调度、智能配电网。

刘 敏