提升弱电网阻尼性能的VSG控制策略研究

班国邦，徐玉韬，袁旭峰，马晓红，欧阳泽宇，吴舟

提升弱电网阻尼性能的VSG控制策略研究

班国邦1,2，徐玉韬1，袁旭峰2，马晓红1，欧阳泽宇1，吴舟2

（1. 贵州电力科学研究院，贵州 贵阳 550002；2. 贵州大学 电气工程学院，贵州 贵阳 550025）

MMC（modular multilevel converter，MMC）直流输配电技术相比传统的直流输配电技术，更适用于向弱交流电网供电的情况。但随着新能源发电渗透率增加，电力系统的等效惯量和等效阻尼逐渐减小，其稳定性问题变得越来越严重。而虚拟同步发电机（virtual synchronous generator，VSG）技术的提出有效地解决这一问题。为进一步提高系统的稳定性，在已有VSG控制技术的基础上，提出了一种基于虚拟电阻的MMC控制策略。首先，介绍了MMC换流器系统的拓扑结构；然后通过建立受端交流电网MMC系统小信号模型分析得出电阻对系统稳定性的影响。在此基础上，对VSG控制技术进行改进，等效增大MMC换流器系统与交流电网之间的电阻，从而提高系统的稳定性；最后，通过PSCAD/EMTDC软件进行仿真计算，结果验证了所提控制策略的正确性。

虚拟电阻；MMC；稳定性分析；柔性直流输配电技术

0 引言

建设稳定、可靠、安全以及环境友好型的新一代电力网络成为时代发展的重要趋势。在此背景下，MMC由于具有较高的电力输送容量、IGBT开关损耗小以及谐波含量少等特点，在柔性直流输电中发挥着巨大的作用[1-3]。

换流器一般采用传统的下垂控制和PI双环控制方式，不能对系统的有功和无功进行独立控制，并且随着新能源发电渗透率的增加，电力系统的等效惯量和等效阻尼也逐渐减小[4]。为解决该问题，国内外众多的专家和学者通过参考传统同步发电机机电暂态和电磁暂态的运行机理，提出了VSG技术[5-10]。在此基础上，若将受端换流器控制为具有同发动机外特性的系统，便可为受端弱交流电网提供电压和频率支撑，其特别适用于向弱交流电网供电[11]。

文献[12]对采用双闭环解耦控制策略的VSG进行小信号建模分析，指出PLL对弱交流电网系统的稳定性具有一定的影响。文献[13]将VSG控制策略应用在MMC受端换流器上，避免了对PLL的使用，有效地抑制了交流电网频率波动，提高了交流系统频率稳定。为解决功率耦合对系统稳定性造成的影响，文献[14]引入了“虚拟阻抗”的物理内涵，即以并网输出电流作为反馈量来修正系统输出电压参考值。通过虚拟阻抗控制可重塑系统的等效输出阻抗，使其呈感性状态，从而实现有功和无功功率解耦。文献[15]则以传统虚拟阻抗功率解耦控制作为基础，通过分析无功环路上的虚拟阻抗作用机理，建立了系统控制器的小信号模型，并从抑制由功率耦合造成的输出电流波动的角度提出了一种改进的功率解耦控制策略。另外，为提高系统的稳定性，文献[16]通过建立VSG在旋转坐标系下的输出阻抗模型，并分析其输出阻抗的频率特性，得出VSG在弱电网下运行易失稳的结论。文献[17]通过利用虚拟电阻提高了采用功率同步控制的受端弱交流电网的稳定性。然而，鲜有文献对虚拟电阻对采用VSG控制的MMC受端弱交流电网的稳定性进行分析。

在柔性直流输配电系统中，系统等值电阻通常很小，VSG控制的稳定性不高，需对其进行优化设计。因此，本文首先在电压调制波处增加电流反馈来等效增大系统和交流电网之间的电阻，并建立MMC与交流电网之间的小信号模型来分析电阻对系统稳定性的影响；然后分析虚拟电阻的作用机理；最后，在PSCAD/EMTDC软件上搭建了两端MMC系统仿真模型，结果验证了所提控制策略的正确性。

1 系统拓扑结构

基于柔性电力电子开关的柔性配电网如图1所示。采用戴维南定理对受端弱交流电网进行等效，其等效电抗为g，等效电压源为s0°。dc为MMC直流侧电压，单相MMC上下桥臂各由个子模块构成，arm和分别为MMC桥臂电感和桥臂电阻，u为变压器一次侧PCC点电压，c∠vc为换流阀出口电压。

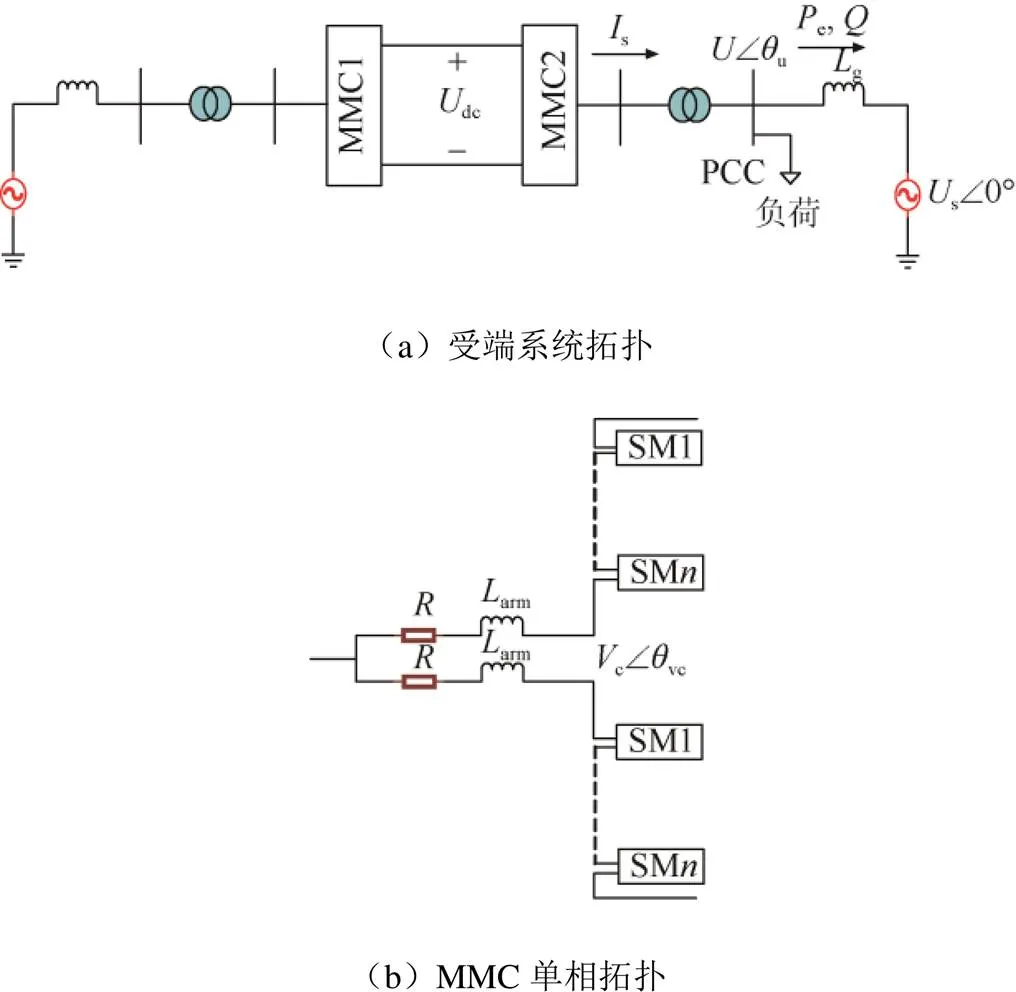
图1 受端弱交流电网MMC拓扑

VSG将传统同步发电机的工作原理引入静止变流器中，用来模拟同步发电机的运行特性，不仅能为电网提供电压和频率支撑，还能使静止变流器具有转动惯量和阻尼特性。控制器拓扑如图2所示。

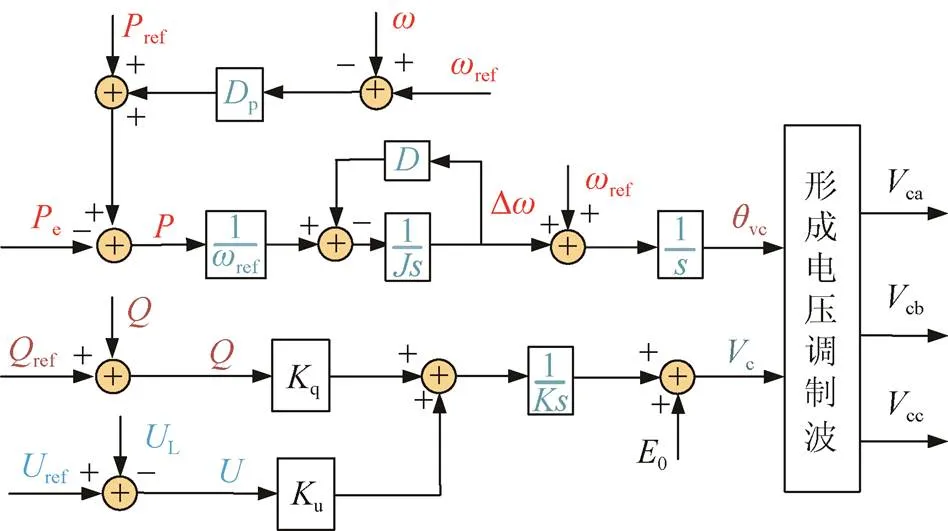
图2 VSG控制框图

图2中VSG控制器主要由有功—频率控制器和无功—电压控制器构成。其中，e为系统输出的有功功率；为系统输出的无功功率；ref、ref、ref分别为输入参考有功、无功功率、参考电压；c为系统参考励磁电动势；L为输出的端电压；vc为VSG的虚拟功角；、ref分别为机械角速度和额定电角速度；为旋转惯量；为阻尼系数；p为调频系数；q、u和分别为无功—电压下垂系数、电压调节系数和积分环节调节系数。

2 系统小信号建模

2.1 系统本体电路小信号建模

为了得到电阻对系统稳定的影响，需要分别建立PCC点有功功率e和电压有效值L与调制波电压幅值c、相角vc的小信号模型。

首先，建立e与c、vc的小信号模型。根据图1可列出表达式（1），其中为MMC换流阀出口至电网之间的等效电感，c[ca,cb,cc]T为电压调制波，s[sa,sb,sc]T为交流电网电压。

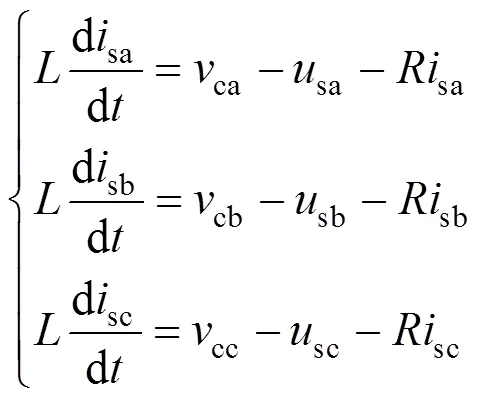
将式（1）进行变换（以电压源方向为轴方向，即sd=s，sq=0）可得到式（2）：

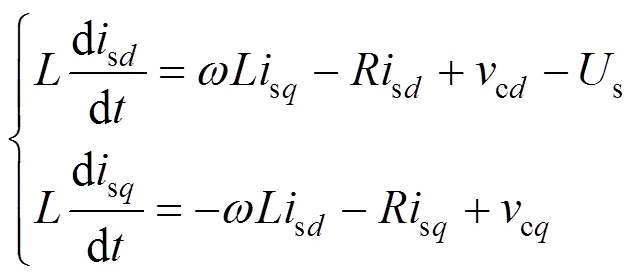
对式（2）进行线性化，可得到其小信号模型如式（3）所示（带“＾”的变量表示该变量的扰动量）：

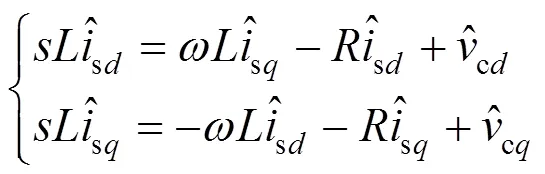
为得到换流阀出口电压分量cd、cq与调制波c、vc的小信号模型，可将cd、cq表示为：

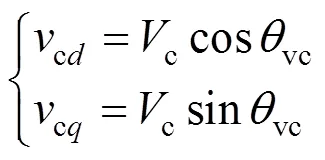
对式（4）进行线性化便可得到流阀出口电压分量cd、cq的小信号模型：

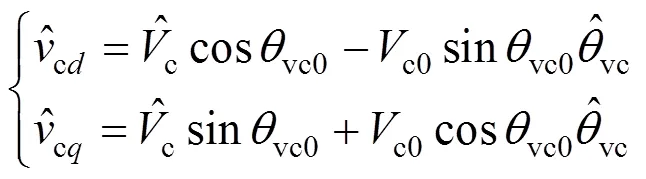
由于换流阀出口至PCC点的阻抗远小于弱交流电网的阻抗，故PCC点的功率近似等于MMC的输出功率：

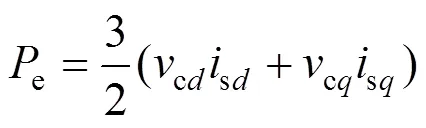
对式（6）进行线性化便可得到功率的小信号模型：

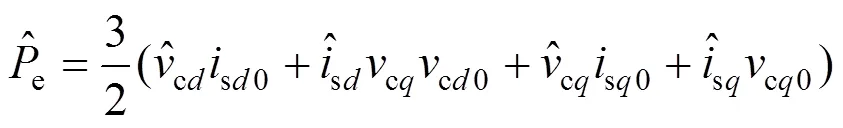
联立式（3）（5）（7）可以得到e与c、vc的小信号模型如下：

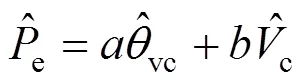
其中：

建立L与c、vc的小信号模型。PCC点电压[a,b,c]T根据前面的计算过程，可类似求出分量的小信号模型如下：

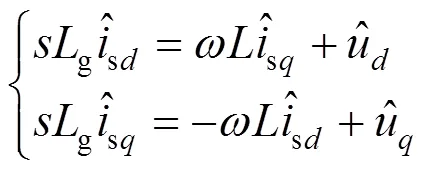
为了得到L的小信号模型，可将其表示为：

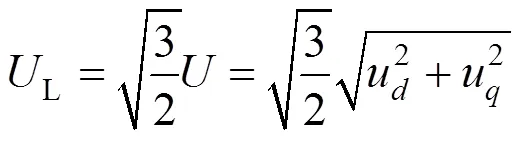
其中：

（16）

2.2 系统控制器小信号建模

根据图2可列出控制器有功环的方程如下：

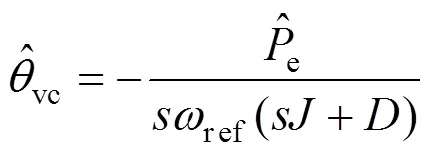
控制器无功环的方程如下：

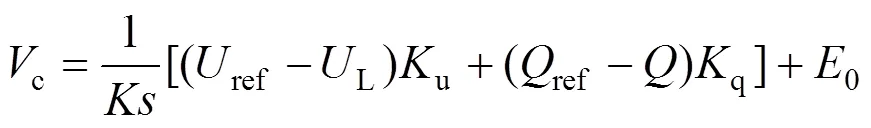
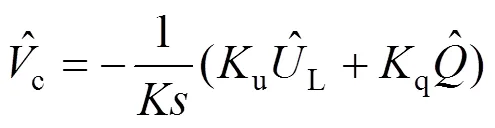
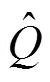
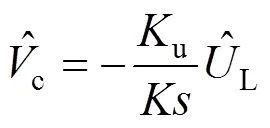
通过以上的计算，可得到系统控制器的小信号模型如下：

（22）

由以上的计算，可得出受端弱交流电网MMC系统的小信号数学模型如图3所示：

图3 受端弱交流电网MMC系统小信号模型

根据图3可得到受端弱交流电网MMC系统的开环传递函数为：

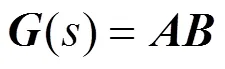
该系统为多输入多输出系统。根据多输入多输出系统零极点理论[17]，可求出()的零点多项式()和极点多项式()如下：

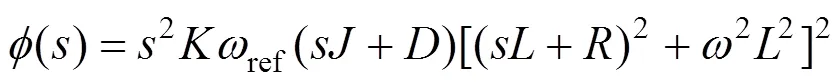
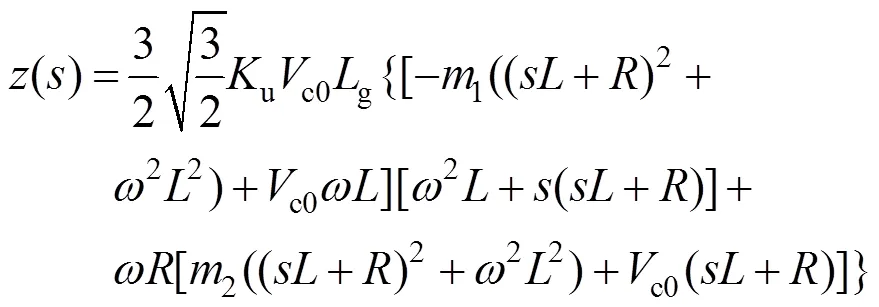
一般情况下，将短路比（short circuit ratio，SCR）小于6～10的电网认为是弱电网，大于20的电网认为是强电网[16]。以系统电阻为增益，分别画出为2.0、2.2、2.5的系统闭环传递函数的根轨迹图，具体如图4所示。

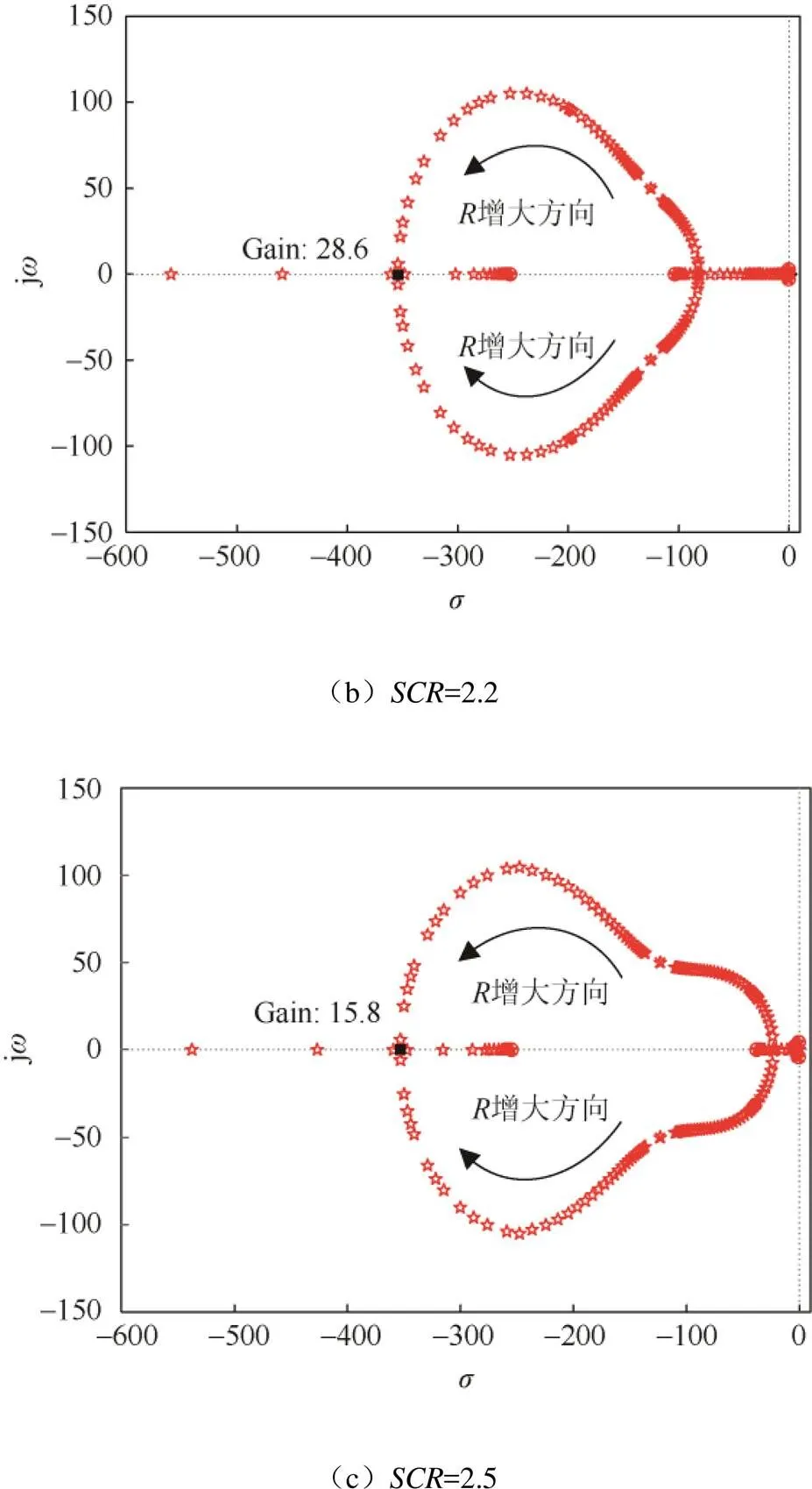
图4 系统根轨迹图

由图4主导极点形成的根轨迹可看出，随着电阻的增大，系统根轨迹朝着负半轴方向移动，系统的稳定性逐渐增强。当电阻减小至0时，系统根轨迹朝着虚轴方向移动，系统稳定性减弱并最终处于稳定边界。

3 虚拟电阻控制策略

虚拟电阻控制器的控制框图如图5所示，通过在MMC控制系统电压调制波生成处增加阀侧电流负反馈环节来矫正电压参考值，以模拟虚拟电阻的作用，从而达到等效增大系统与电网之间的电阻的效果。图中，c表示经过虚拟电阻矫正后的电压调制波。

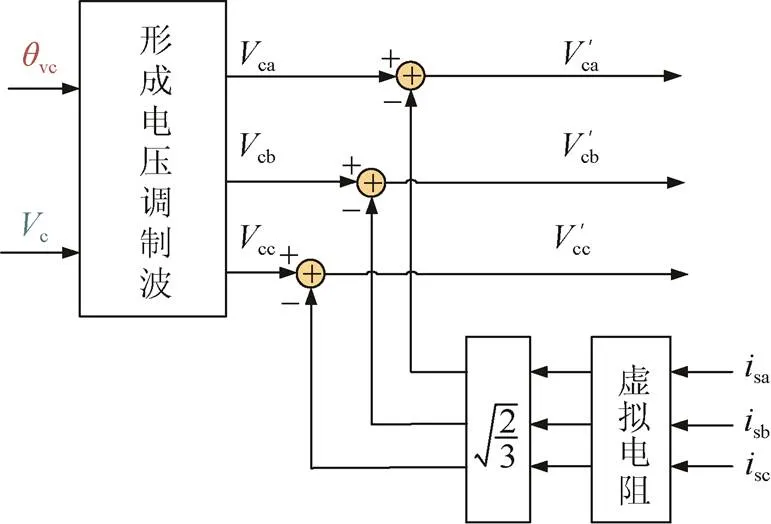
图5 虚拟电阻控制器控制框图

虚拟电阻控制策略是一种改进的VSG控制策略，虚拟电阻vir不是实际存在的电阻，其存在没有使系统增加运行损耗，反而提高了系统的稳定性，其作用机理如图6所示。

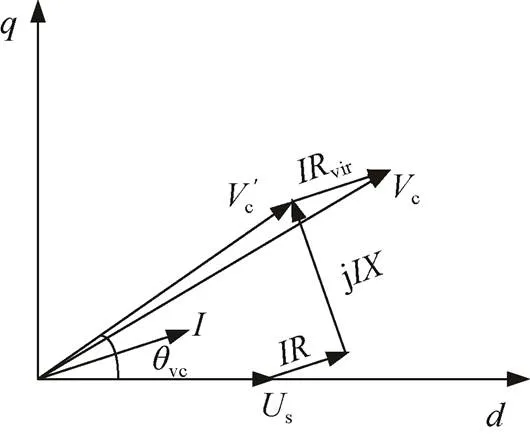
图6 虚拟电阻作用机理图

图6中为对应的电感值，当系统采用虚拟电阻控制策略时，系统与电网之间的功角vc将会减小，根据功角特性曲线可知，系统的稳定性将得到提高，并且随着虚拟电阻vir的增大，功角vc将逐渐减小，系统的稳定性越来越强。虚拟电阻的最大取值可参考文献[16]提出的方法：

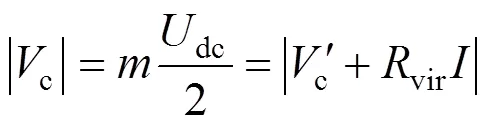
式中：为MMC的调制比，且≤1。由于vir的取值受到了式（26）的约束，使系统电阻无法取到图4中的最佳增益[16]。

4 仿真验证

为验证上述分析的正确性，在PSCAD/ EMTDC仿真平台上搭建了两端MMC柔性配电网进行仿真实验分析，其系统参数如表1所示。

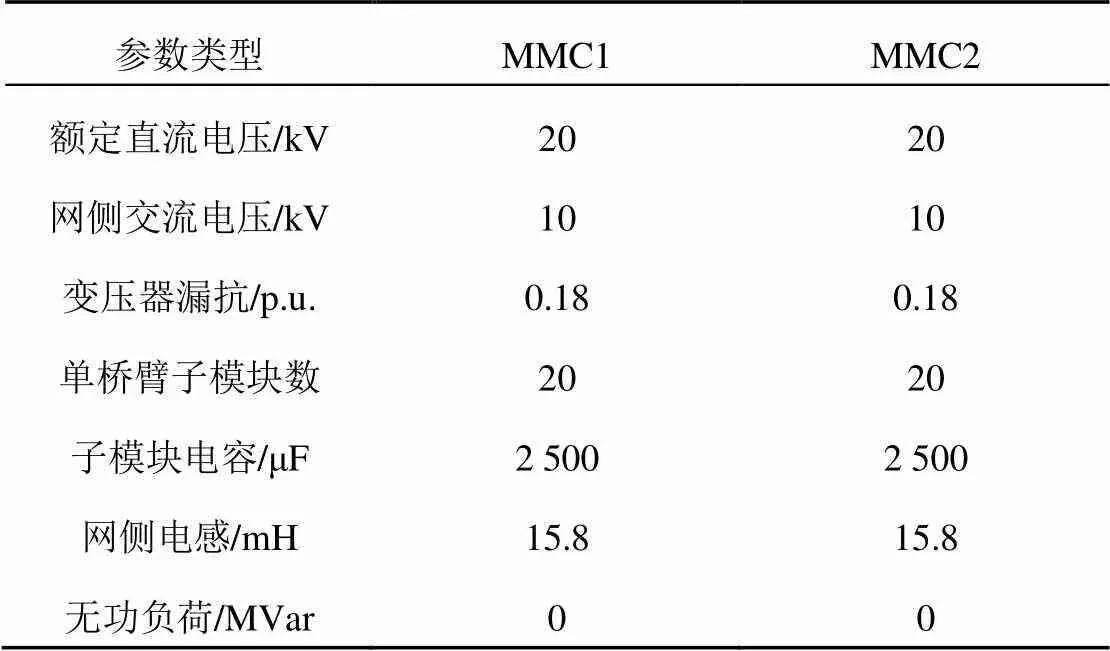
表1 两端MMC系统仿真参数

MMC换流器的参考有功功率为10 MW，控制器中=25 kg∙m2，=10 N∙m∙s/rad，=u=1。为了便于对系统仿真图形进行观察，设置系统在=0.6 s时开始运行，具体仿真过程为：

（1）在=0.6 s时，MMC系统并入强电网运行，此时交流电源的等值电感g=1.6 mH（标幺值为0.05，对应的为20）。

（2）在=1.5 s时，MMC系统由强电网转入弱电网运行，此时交流电源的等值电感g=15.8 mH（标幺值为0.47，对应的为2）。

（3）在=3 s时，MMC系统接入vir=1 Ω的虚拟电阻，此前MMC系统的vir=0；在=8 s时，系统切除虚拟电阻。仿真图形如图7所示。

由图7可以看出，系统在=0.6 s时开始运行，且在到达1.5 s之前，由于MMC系统接入的是强电网，能够稳定运行。当=1.5 s时，MMC系统由强电网转入弱电网运行，此时其电流、交直流侧电压以及功率等开始发生振荡；由于没有投入虚拟电阻，均呈发散状态而无法稳定运行。当=3 s时，系统开始投入虚拟电阻，各参量的振荡开始减小，并朝着系统稳定的方向运行，直至系统稳定运行。图7（b）中，当虚拟电阻投入大约2 s后，交流侧电压有效值就能稳定在10 kV左右。图7（c）中，当虚拟电阻投入大约0.2 s后，直流侧电压能稳定在20 kV左右。图7（d）证明了投入虚拟电阻后，VSG系统能够按照预设的ref输出有功功率，并且能够稳定运行。当=8 s时，切除虚拟电阻，MMC系统的各参量又呈发散状态，系统开始失稳。以上的仿真结果证明了所提虚拟电阻控制策略的正确性。

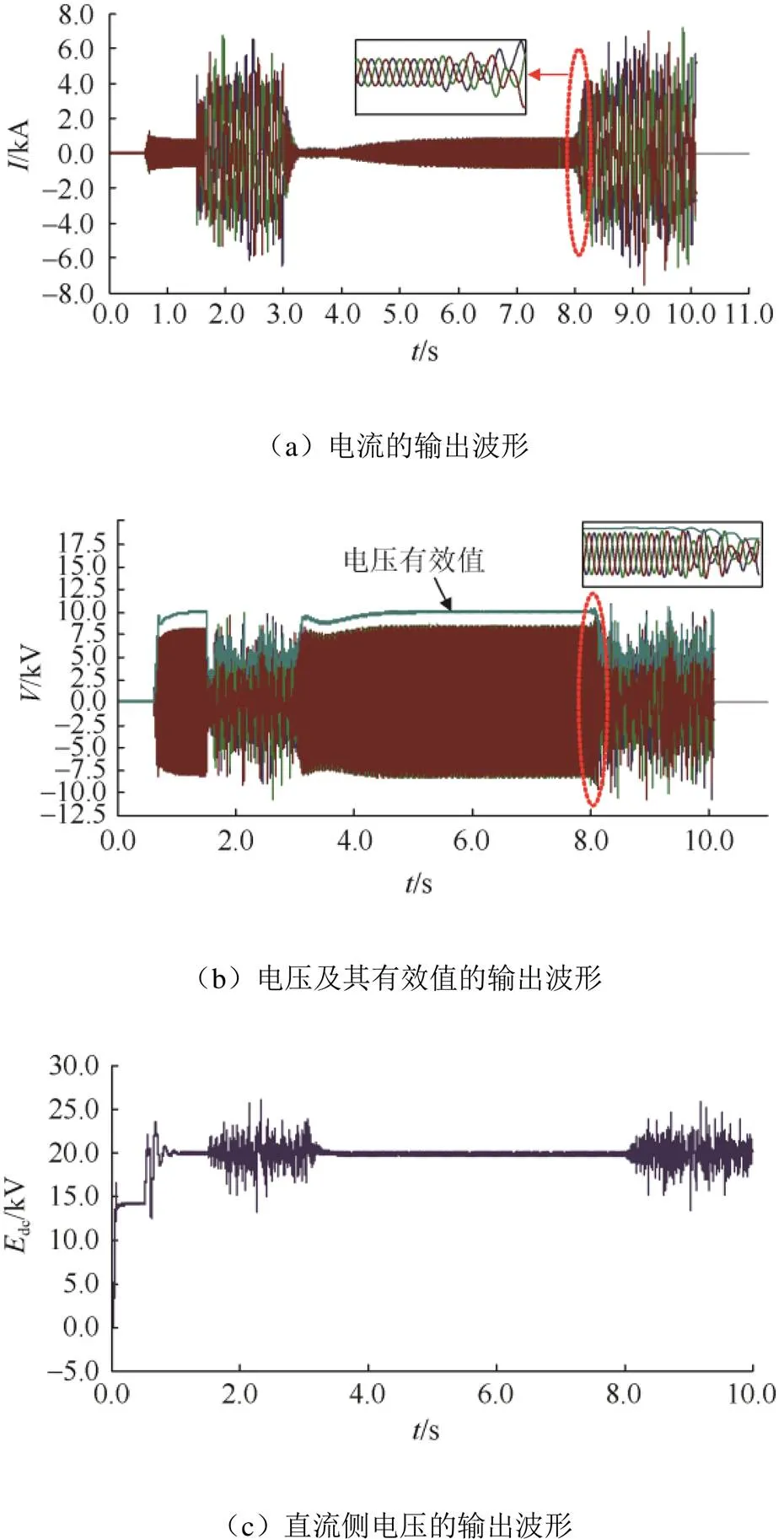
为了验证虚拟电阻对系统稳定性能的影响，分别利用阻值为2 Ω和6 Ω的虚拟电阻进行了仿真试验，仿真结果如图8所示。

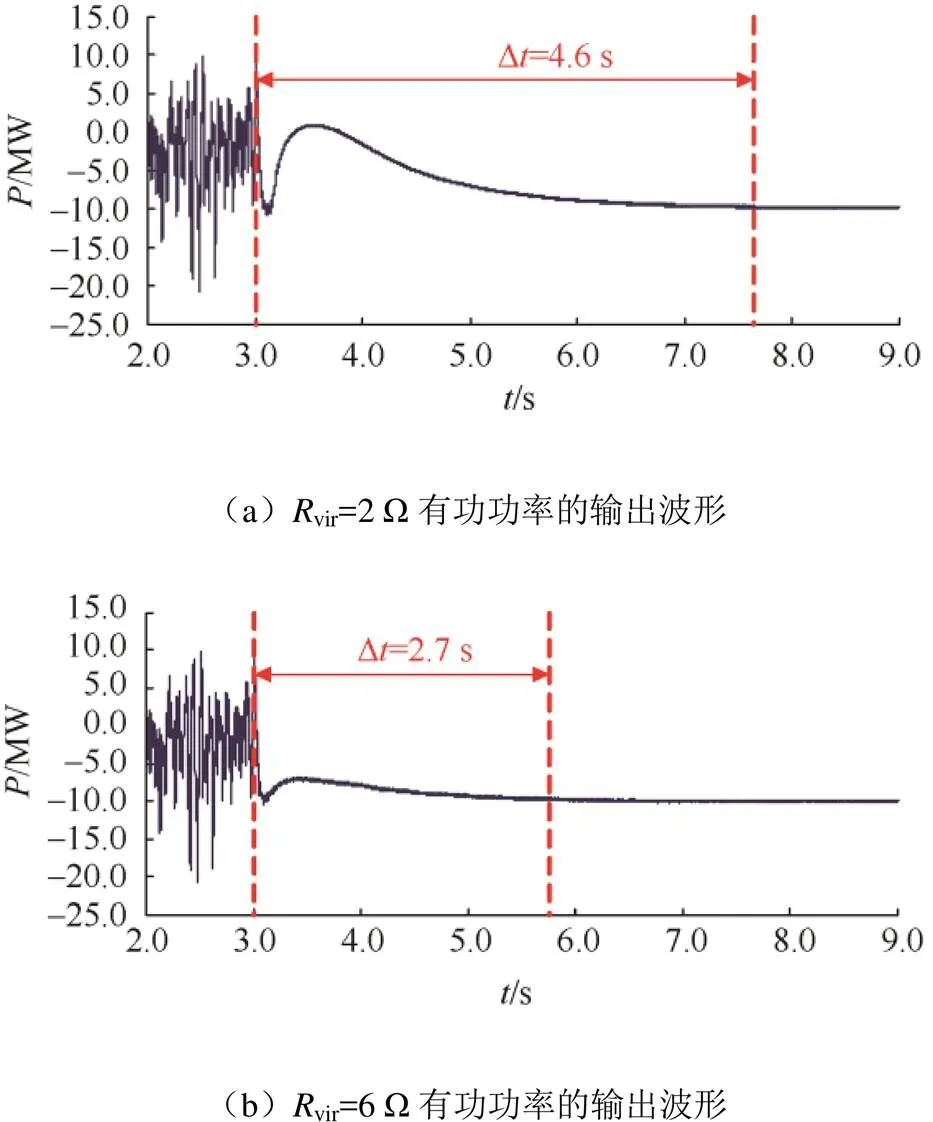
图8 不同Rvir时系统的有功功率输出波形

从图8（a）可看出，当投入2 Ω的虚拟电阻以后，系统经过4.6 s左右才能达到稳定状态；而从图8（b）可看出，当投入的虚拟电阻为6 Ω时，系统经过2.7 s左右就达到了稳定状态，后者使系统到达稳定状态所需的时间比前者少了1.9 s。同时，在系统投入vir后的暂态过程中，后者的有功功率波动范围比前者小，且波动过程也更加平缓，这体现了随着vir的增大，系统的阻尼性能越好。由仿真结果可知，随着虚拟电阻的增大（vir不能超过对应的最大值），VSG系统的暂态波动越小，达到稳态所需的时间越少，系统的稳定性越强，这也验证了理论分析的正确性。

为了验证功率波动对系统稳定性能的影响，在=8 s时，令系统ref从10 MW减小到5 MW（此处对应的vir=2 Ω，且在=3 s后，vir一直投入运行），仿真结果如图9所示。

图9 Pref变化时系统的有功功率输出波形

从图9中可看到，在=8 s时，系统输出的有功功率开始减少，经过0.6 s后从10 MW减到5 MW，并能继续稳定运行。仿真结果验证了所提控制策略能使系统在功率波动的情况下也能继续稳定运行。

5 结论

针对柔性直流输配电系统中因系统等值电阻较小而导致的稳定性问题，本文提出了一种基于虚拟电阻的VSG改进控制策略。通过分析研究得到以下结论：当柔性直流输配电系统的等值电阻较小或接近于0时，系统处在临界稳定状态；通过加入虚拟电阻控制以等效增大系统等值电阻，将使系统从临界稳定状态变为稳定状态，且虚拟电阻越大（不能超过某一临界值），系统稳定性越强。

[1] 常立国, 苟锐锋, 杨晓平, 等. 适用于MMC-HVDC的优化均压策略[J]. 高电压技术, 2020, 46(5): 1720-1729.

CHANG LIGUO, GOU RUIFENG, YANG XIAOPING, et al. Optimized voltage balancing strategy for MMC-HVDC[J]. High Voltage Engineering, 2020, 46(5): 1720-1729(in Chinese).

[2] 汤广福, 罗湘, 魏晓光. 多端直流输电与直流电网技术[J]. 中国电机工程学报, 2013, 33(10): 8-17.

TANG GUANGFU, LUO XIANG, WEI XIAOGUANG. Multi-terminal HVDC and DC-grid technology[J]. Proceedings of the CSEE, 2013, 33(10): 8-17(in Chinese).

[3] 郑天文, 陈来军, 陈天一, 等. 虚拟同步发电机技术及展望[J]. 电力系统自动化, 2015, 39(21): 165-175.

ZHENG TIANWEN, CHEN LAIJUN, CHEN TIANYI, et al. Review and prospect of virtual synchronous generator technologies[J]. Automation of Electric Power Systems, 2015, 39(21): 165-175(in Chinese).

[4] 祁琪, 姜齐荣, 许彦平. 智能配电网柔性互联研究现状及发展趋势[J]. 电网技术, 2020, 44(12): 4664-4676.

QI QI, JIANG QIRONG, XU YANPING. Research status and development prospect of flexible interconnection for smart distribution networks[J]. Power System Technology, 2020, 44(12): 4664-4676(in Chinese).

[5] ZHONG Q C, WEISS G. Synchronverters: inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.

[6] LI C, XU J, ZHAO C. A coherency-based equivalence method for MMC inverters using virtual synchronous generator control[J]. IEEE Transactions on Power Delivery, 2016, 31(3): 1369-1378.

[7] ALIPOOR J, MIURA Y, ISE T. Power system stabilization using virtual synchronous generator with alternating moment of inertia[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(2): 451-458.

[8] 程启明, 余德清, 程尹曼,等. 基于自适应旋转惯量的虚拟同步发电机控制策略[J]. 电力自动化设备, 2018, 38(12): 79-85.

CHENG QIMING, YU DEQING, CHENG YINMAN, et al. Control strategy of virtual synchronous generator based on adaptive rotational inertia[J]. Electric Power Automation Equipment, 2018, 38(12): 79-85(in Chinese).

[9] 吴舟, 邹晓松, 袁旭峰, 等. 计及储能动态的VSG惯量阻尼自适应控制研究[J]. 电网与清洁能源, 2020, 36(12): 83-91.

WU ZHOU, ZOU XIAOSONG, YUAN XUFENG, et al. Research on VSG rotational inertia and damping adaptive control considering energy storage dynamics[J]. Advances of Power System & Hydroelectric Engineering, 2020, 36(12): 83-91(in Chinese).

[10] 宋琼, 张辉, 孙凯,等. 多微源独立微网中虚拟同步发电机的改进型转动惯量自适应控制[J]. 中国电机工程学报, 2017, 37(2): 412-423.

SONG QIONG, ZHANG HUI, SUN KAI, et al. Improved adaptive control of inertia for virtual synchronous generators in islanding micro-grid with multiple distributed generation units[J]. Proceedings of the CSEE, 2017, 37(2): 412-423(in Chinese).

[11] 苑宾, 李探, 许建中, 等. 联接弱交流电网MMC系统小信号稳定性分析[J]. 中国电机工程学报, 2017, 37(18): 5339-5349.

YUAN BIN, LI TAN, XU JIANZHONG, et al. Small-signal stability analysis of modular multilevel converter connected to a weak AC system[J]. Proceedings of the CSEE, 2017, 37(18): 5339-5349(in Chinese).

[12] ZHOU J Z, DING H, FAN S, et al. Impact of short-circuit ratio and phase-locked-loop parameters on the small-signal behavior of a VSC-HVDC converter[J]. IEEE Transactions on Power Delivery, 2014, 29(5): 2287-2296.

[13] 陈继开, 曾强, 李林, 等. 基于虚拟同步发电机的MMC受端换流器控制策略[J]. 现代电力, 2020, 37(4): 408-415.

CHEN JIKAI, ZENG QIANG, LI LIN, et al. Control strategy of MMC receiving converter based on virtual synchronous generator[J]. Modern Electric Power, 2020, 37(4): 408-415(in Chinese).

[14] 杨东升, 阮新波, 吴恒. 提高LCL型并网逆变器对弱电网适应能力的虚拟阻抗方法[J]. 中国电机工程学报, 2014, 34(15): 2327-2335.

YANG DONGSHENG, RUAN XINBO, WU HENG. A virtual impedance method to improve the performance of LCL-type grid-connected inverters under weak grid conditions[J]. Proceedings of the CSEE, 2014, 34(15): 2327-2335(in Chinese).

[15] 李旭枫, 陆立民, 成乐祥, 等. 基于自适应虚拟阻抗改进无功环路的虚拟同步功率解耦控制策略[J]. 电网技术, 2019, 43(10): 3752-3760.

LI XUFENG, LU LIMIN, CHENG LEXIANG, et al. Power decoupling control strategy in virtual synchronous generator with improved reactive power loop based on adaptive virtual impedance[J]. Power System Technology, 2019, 43(10): 3752-3760(in Chinese).

[16] 韩刚, 蔡旭. 虚拟同步发电机输出阻抗建模与弱电网适应性研究[J]. 电力自动化设备, 2017, 37(12): 116-122.

HAN GANG, CAI XU. Output impedance modelling of virtual synchronous generator and its adaptability study in a weak grid[J]. Electric Power Automation Equipment, 2017, 37(12): 116-122(in Chinese).

[17] 苑宾, 许建中, 赵成勇, 等. 利用虚拟电阻提高接入弱交流电网的MMC小信号稳定性控制方法[J]. 中国电机工程学报, 2015, 35(15): 3794-3802.

YUAN BIN, XU JIANZHONG, ZHAO CHENGYONG, et al. A virtual resistor based control strategy for enhancing the small-signal stability of MMC integrated in weak AC system[J]. Proceedings of the CSEE, 2015, 35(15): 3794-3802(in Chinese).

Research on VSG Control Strategy for Improving Damping Performance of Weak Grid

BAN Guobang1,2, XU Yutao1, YUAN Xufeng2, MA Xiaohong1, OUYANG Zeyu1, WU Zhou2

(1. Guizhou Electric Power Research Institute, Guiyang 550002, China;2. The Electrical Engineering College, Guizhou University, Guiyang 550025, China)

Compared with traditional DC transmission and distribution technology, MMC (cmodular multilevel converter) DC transmission and distribution technology is more suitable for supplying power to weak AC grid. However, as the permeability of new energy generation increases, the equivalent rotational inertia and equivalent damping of the power system gradually decrease, and its stability problem becomes more and more severe. The virtual synchronous generator (VSG) technology can effectively solve this problem. In order to further improve the stability of the system, based on the existing VSG control technology, Proposes a virtual resistance-based MMC control strategy. First, the topologies of the MMC converter system are introduced, and then, the influence of resistance on system stability is obtained by establishing a small signal model of the AC grid MMC system at receiving end. On this basis, the VSG control technology is improved to equivalently increase the resistance between the MMC converter system and the AC grid, thereby improving the stability of the system. Finally, the simulation calculation is carried out through PSCAD/EMTDC software, and the result verifies the proposed control strategy’s correctness.

virtual resistance; MMC; stability analysis; flexible DC transmission and distribution technology

TM761

A

1672-0792(2021)08-0010-08

10.3969/j.ISSN.1672-0792.2021.08.002

2021-05-14

国家自然科学基金（52067004）；贵州省科学技术基金（黔科合基础[2019]1128号）；贵州电网公司科技项目（GZKJXM20182104）

班国邦（1982—），男，高级工程师，研究方向为高电压电气技术；

徐玉韬（1982—），男，高级工程师，研究方向为柔性直流配网运行与控制，分布式电源及微电网；

袁旭峰（1976—），男，教授，研究方向为电力电子在电力系统中的应用，电力系统运行与控制；

马晓红（1978—），女，高级工程师，研究方向为高电压与绝缘技术；

吴 舟（1995—），男，硕士研究生，研究方向为基于自适应旋转惯量的MMC换流器虚拟阻抗控制技术。