基于生成对抗网络的多模态可变形医学图像配准

宋 枭，朱家明，王 莹

(扬州大学 信息工程学院，江苏 扬州 225000)

0 引言

图像配准是图像处理中的一个重要领域，旨在找寻多幅图像之间最优空间映射，使得2幅或多幅图像的相关像素点唯一对应[1]。医学图像是疾病筛查及诊断的重要依据，不同模态的医学图像反映人体组织或器官的侧重点不同。医学图像配准是医学图像融合的前提，可以有效帮助医护人员进行病灶定位、疗效评估、术前规划和术中导航[2]。

传统的基于互信息和结构特征的医学图像配准目的在于通过长时间的迭代最大化图像强度之间的统计相关性以及最大化基于结构表示的结构度量，不断减小图像映射之间的差异[3]。调整线性变换的相关参数很容易减小线性差异对配准结果的影响，然而非线性的局部形变难以配准，因此需要通过网络充分学习图像之间的映射以解决该问题[4]。Guha等人[5]提出了Voxelmorph配准模型，利用Unet网络学习到的参数直接计算函数获取配准场，大幅缩短了配准时间； Zhao等人[6]提出了级联递归配准模型，将每个子网络的输出作为后一个子网络的输入，渐进生成形变场，有效降低了网络学习的难度；Mahapatra等人[7]提出了基于生成对抗网络(Generative Adversarial Networks,GANs)的形变配准模型，将医学图像的灰度作为概率测度，用概率来表示配准效果，避免了耗时的迭代，直接生成形变场与配准图像。为了提高GANs形变配准能力，本文提出了一种结合GANs、级联网络和Unet的医学图像配准模型，考虑到标准卷积不能提取形变特征，将形变卷积嵌入到Unet的下采样过程中，并在上采样过程中融入形变特征。

1 形变配准模型

1.1 形变配准

由于计算机体层成像(Computed Tomography,CT)、核磁共振(Magnetic Resonance Image,MRI)的层间距、层厚不一致，导致成像结果不完全对齐，表现在人体组织或器官的非线性形变，如图1所示。第一行中腹部分割结果展示了图像不对齐导致的器官非线性形变。即使在同一种成像技术下，不同成像参数也会造成一定的非线性形变；第二行中红色和蓝色标注的MRI成像过程中不同弛豫时间脑部组织或病灶的非线性形变。

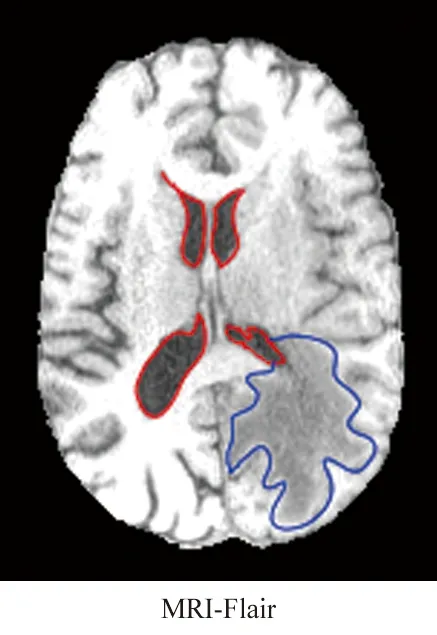
图1 非线性局部形变Fig.1 Nonlinear local deformation

假设浮动图像lm、固定图像lf定义在二维空间域Ω⊂R中，以θ为参数的形变场是一个映射φθ:Ω→Ω。对于形变配准而言，旨在构建一个形变场预测函数Fθ(lm,lf)=φθ，浮动图像lm在形变场预测函数的作用下得到与固定图像空间对齐的形变图像lw=lm∘φθ，其中∘表示形变场作用在浮动图像上。

1.2 级联模型

图2 级联模型Fig.2 Cascade model

(1)

(2)

(3)

(4)

1.3 生成器结构

在卷积神经网络(Convolutional Neural Networks,CNNs)中同一层的激活单元具有相同的感受野，但不同位置对应着不同尺度或形变的物体，因此自适应调整感受野是精确提取形变特征的关键[8]。Dai等人[9]提出的可形变卷积网络(Deformable Convolution Networks,DCNs)有效提高了CNN的形变建模能力。DCNs在特征图中增加了额外的偏移量，从目标任务中学习到的特征矩阵相较于标准卷积增加了一个偏移矩阵[10]。Wang等人[11]将DCNs引入图像配准，将2N个偏移输出修改为2个偏移输出，将变形直接应用于输入图像，其结构如图3所示。

图3 形变卷积Fig.3 Deformable convolution

可变形卷积灵活的感受野，增加了网络空间形变的适应性。可变形卷积对特征图的每个位置学习一个偏移量，用2个偏移场表示X轴和Y轴的偏移。对于一个3×3的卷积，每次输出都要采样9个位置，传统的卷积输出为：

(5)

式中，R={(-1,-1),(-1,0),…,(0,1),(1,1)}表示卷积核中的9个位置；w(pn)表示加权采样；x(p0) 表示每次作用在图像上卷积核的中心位置。

可变形卷积在传统卷积上增加了一个偏移量Δpn，此时卷积输出为：

(6)

本文生成结构以Unet为基础，在每次下采样过程中添加偏移卷积层，使空间形变在每次下采样过程中逐层编码，并将形变的特征信息跳跃连接至上采样阶段，使形变特征逐级还原，其结构如图4所示。生成结构的具体网络参数如表1所示，表中k3n64s1表示64个大小为3 pixel×3 pixel,步长为1的卷积核。

图4 生成网络结构Fig.4 The structure of generative network

表1 生成网络参数Tab.1 The parameters of generative network

1.4 判别器结构

判别器的目的在于鉴定形变图像与参考的固定图像之间的配准程度。判别器通过阈值函数将输出映射到0和1之间，当输出越接近1时代表配准程度越高，越接近0时配准程度越低[12]。本文判别器由8个卷积层和2个全连接层组成，结构如图5所示。图5中8个卷积层的卷积核大小均为3 pixel×3 pixel，步长为1或2，当步长为1时图像尺寸不变，当步长为2时图像尺寸减小为原来的一半，卷积核数量由64个成倍增加到512个，最终提取到512个16 pixel×16 pixel的特征图。接着第一个全连接层用1 024个神经元将二维特征图转换成一维数组，第二个全连接层用一个神经元经阈值函数完成预测输出。判别网络的具体参数如表2所示，表中k3n64s1表示64个大小为3 pixel×3 pixel,步长为1的卷积核。

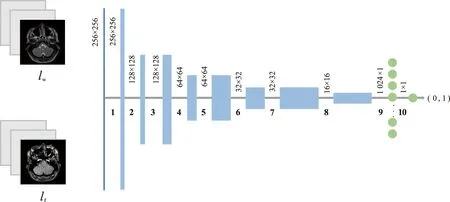
图5 判别网络结构Fig.5 The structure of discriminative network

表2 判别器网络参数Tab.2 The parameters of discriminator network

2 构造损失函数

2.1 生成器损失

大部分学者提出的基于信息论的配准方法诸如NMI、CCRE等是基于香农熵构造的，而Antolin等[13]指出香农熵的可加性并未考虑2个独立随机变量之间的相互作用。为此，李碧草等人[14]根据具有伪性的Arimoto熵提出了可用来量化随机变量概率分布之间距离的詹森Arimoto散度(Jensen Arimoto Divergence，JAD)。

假设一个概率分布为p=(p1,p2,…,pk)的随机变量x(x1,x2,…,xk)，则x的Arimoto熵为：

(7)

式中，α是衡量伪可加程度的参数，α>0 且α≠1，当α趋于1时Arimoto熵等于香农熵；Aα(·) 表示Arimoto熵。概率分布P的JAD定义为：

(8)

式中，ωi表示加权因子，ωi≥0且∑ωi=1。

GANs类似极大似然估计，通过模拟数据概率分布，使得概率分布与观测数据的概率统计分布一致或者尽可能接近[15]。对于生成的形变图像lw=lf∘φθ和固定图像lf，将其灰度值看作随机变量，则它们的联合熵为：

(9)

詹森Arimoto散度为：

(10)

式中，α>0 且α≠1；fi，wj表示固定图像和生成形变图像的灰度级；p(fi)，p(wj)，p(wj|fi)分别表示固定图像和形变图像不同灰度级的概率分布以及2幅图像的条件概率分布。

为了保证生成的形变图像与参考的固定图像之间结构信息相似，引入局部梯度项，那么相似性损失为：

(11)

式中，‖表示L2距离，此时生成器损失函数表示为：

(12)

(13)

式中，x，y表示图像X、Y轴方向上的尺寸。

当lw与lf完全配准时，相似度最大，此时生成器的参数θ最优化过程为：

(14)

2.2 判别器损失

对于有限训练样本xi∈X,yi∈Y，GANs的目的在于训练2个生成器G:X→Y,F:Y→X，和2个判别器DX,DY，DX用于区分样本xi和生成数据F(y)，DY用于区分样本yj和生成数据G(x) 。对抗损失为：

Ladv(G,DY,X,Y)=Ey∈p(y)[lgDY(y)]+

Ex∈p(x)[lg(1-DY(G(x)))]。

(15)

对于浮动图像lf和固定图像lm，对抗损失为Ladv(G,Dm,lf,lm)。

生成对抗网络能够任意变换输入图像以匹配目标域的分布，循环一致损失能够保持形变的微分同胚性即可以平滑地进行正向和反向的形变[16]，表示为：

Lcyc(G,F)=Ex‖F(G(x))-x‖1+Ey‖G(F(y))-y‖1。

(16)

因此，总的目标函数为：

L(G,F,Dlm,Dlf)=Ladv(G,Dlf,lm,lf)+Ladv(F,Dlm,lf,lm)+

ηLcyc(G,F)，

(17)

式中，η是循环一致损失的加权系数。

3 验证分析

3.1 实验环境

本文实验以Pytorch为框架，使用Adam优化算法，学习率设置为0.000 1，每更新2次判别器后更新生成器。由于硬件环境限制，仅将训练批次设置为1，级联次数设置为3。用基于ITK开发的Elastix和同样基于Unet网络构造的VoxelMorph模型(简称Vm模型)对比本文模型，为了提升运行速度，将Elastic配准工具配置在3D-slicer的GPU环境中。

3.2 实验数据

本文使用MICCAI BraTS 2018分割挑战赛和Learn2Reg 2021配准挑战赛中的数据作为实验数据，其中BraTS 2018收集了大量脑部肿瘤MRI数据，训练集共有285个病例，每个病例包括4种MRI序列：T1、T1ce、T2和Flair，尺寸为240 pixel×240 pixel×155。Learn2Reg 2021收录了来自TCIA、BCV、CHAOS的122对经过裁剪、重采样等预处理的腹部MRI和CT成像。

3.3 评估指标

均方差误差(Root Mean Square Error,RMSE)是反映估计量和被估计量之间的差异程度的一种度量，本文用来度量配准前后图像灰度概率分布之间的差异[18]。其值越小，模型拟合程度越高，生成的形变图像越接近参考的固定图像 ，定义为：

(18)

式中，t表示像素点的位置；P表示所有像素点的位置。

峰值信噪比(Peak Signal to Noise Ratio,PSNR)是峰值信号能量与噪声平均能量之间的比值，本文用于评估配准图像的质量，其值越小失真越大。当PSNR值低于20 dB时，配准图像质量将严重失真[17]，定义为：

(19)

式中，MAX为图片最大像素值。

结构相似性(Structural Similarity,SSIM)，从图像组成的角度将结构信息定义为独立于亮度、对比度的反映场景中物体结构的属性，并将失真建模为亮度、对比度和结构3个不同因素的组合[19]，其值越大结构越相似，定义为：

(20)

式中，μlw为形变图像的均值；μlf为固定图像的均值；σlw为形变图像的方差；σlf为固定图像的方差；σlwlf为形变图像和固定图像的协方差；c1,c2为常数。

3.4 实验结果

对核磁共振T2和Flair图像进行双向配准，配准结果如图6所示。图中第一行配准结果的固定图像是Flair，浮动图像是T2，第二行配准结果的固定图像是T2，浮动图像是Flair。T2图像能够清晰反应脑部肿瘤及肿瘤团块周围的水肿带，而Flair图像对肿瘤团块反映不明显，且2幅图像在水肿带边沿存在明显的形变。

T2

为了更加直观地对比配准效果，对配准结果进行伪彩色处理，效果如图 7所示。用蓝色、白色线框分别标注脑部肿瘤以及侧脑室三角区。

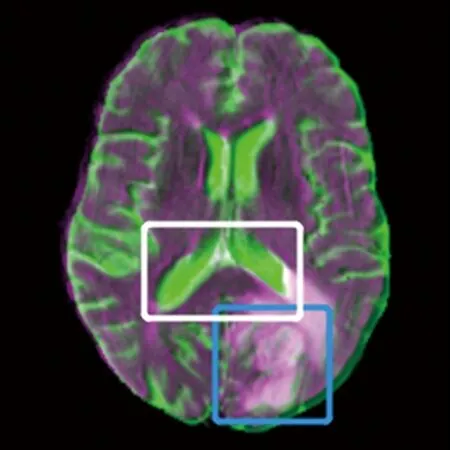
Elastix(T2-Flair)

由图7可以看出，本文模型在脑肿瘤配准结果中水肿带边沿红绿伪影较少，且在侧脑三角室部分重合度高于其他2种模型，配准效果明显优于其他2种模型。

Flair和T2图像配准的指标结果如表3所示。

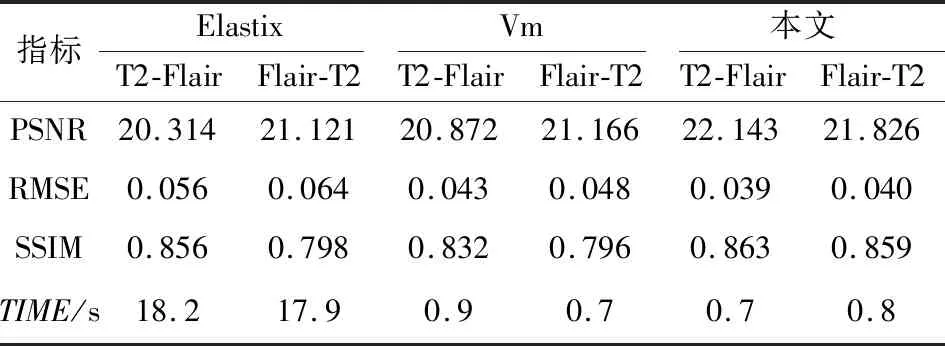
表3 Flair，T2配准数据Tab.3 Registration data for Flair and T2

从表中可以看出，本文模型双向配准的PSNR、SSIM均高于Elastix和Vm模型，RMSE、TIME均低于Elastix和Vm模型，说明本文的配准精度和配准时间优于其他2种模型。此外，Elastix模型双向配准结果差异率的绝对值分别为3.82%,12.50%,6.78%和1.65%，Vm模型双向配准的差异率的绝对值分别为1.39%,10.42%,4.33%和22.22%，本文模型双向配准的差异率的绝对值分别为1.43%,2.50%,4.63%和12.5%。上述数据中本文模型的双向配准差异率与Vm模型相当，但前三者明显低于Elastix模型，说明基于本文模型具有较好的双向配准能力。

为了对比不同成像技术下的形变配准效果，本文对腹部的CT和MR图像进行配准，配准结果如图8所示。用红色箭头标注局部形变配准欠缺的地方，可以看出Elastix模型中箭头数量较多，Vm模型其次，本文模型最少，说明本文模型在CT和MR形变配准中具有明显的优势。

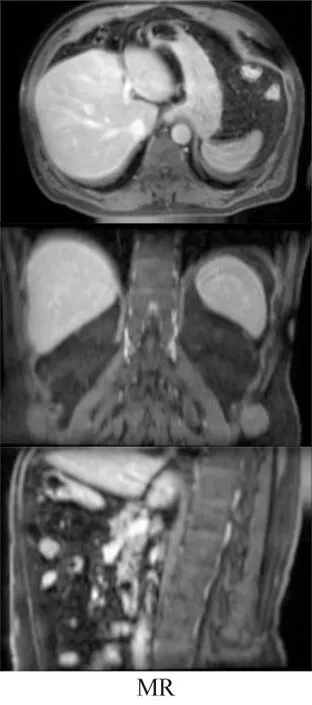
图8 MR,CT配准案例Fig.8 Example results for MR and CT registration

MR和CT图像配准指标结果如表4所示。可以看出，本文模型的PSNR、SSIM、TIME均优于Elastix和Vm模型，尽管RMSE略高于Elastix，但本文模型的形变图像与参考的固定图形具有较高的相似度且失真较小。

表4 MR、 CT配准数据Tab.4 Registration data for MR and CT

4 结束语

本文提出了一种基于生成对抗网络的可变形医学图像配准模型。该模型将可变形卷积和级联结构引入生成模块，提取形变特征，从而使模型具有形变配准的能力； 用JAD散度代替原始GAN网络中的JS散度，考虑了2个随机概率分布之间的相关性，提高了配准的精度；级联了3个生成器，使形变场逐级优化，进一步提高了配准的精度。基于不同评估指标的实验表明，本文模型具有较好的配准精度和形变配准能力。