强混响及噪声相关背景下说话人跟踪方法
2021-09-07杨海红王琳娟
杨海红,王琳娟
(1.山西旅游职业学院 计算机科学系,山西 太原 030031;2.山西农业大学 基础部,山西 晋中 030801)
0 引言
说话人位置的准确定位和跟踪是人工智能领域研究热点问题,近年来,受到了国内外研究人员的广泛关注[1-4]。为克服虚拟声源的影响,研究人员将粒子滤波方法引入到说话人跟踪系统中,取得了很大的改进,一定程度上克服了虚拟声源的影响[3-10]。其主要特点是说话人的位置信息是根据最新的观测信息随着时间进行递推估计的,通过采用一个Markov说话人运动模型将说话人的位置状态信息进行实时的递归处理[11-13]。可以看出,基于滤波方法的说话人跟踪方法充分利用了说话人的运动信息和时间的相关性,可以有效地克服传统方法中存在的虚拟声源干扰问题,提升了噪声背景下说话人的位置定位和跟踪精度[14-16]。但是这些研究存在着一个缺陷,即说话人发音的连续性。假设说话人一直处于发声状态,且跟踪的时间只有一个人在活动。很明显,这种假设是不符合实际应用场景的,特别是在有多人参与的会议场景,经常会出现语音的静默,以及多个人的交叉说话。且多人交互说话情况往往导致背景噪声的恶化和相关性,导致现有非线性滤波方法的跟踪精度降低。基于此,本文针对强混响及噪声相关背景下说话人跟踪问题,提出了一种解相关粒子滤波跟踪方法。该方法的主要创新有2点:一是利用状态方程恒等变换和矩阵相似变换理论实现了过程噪声和量测噪声的解相关;二是随机有限集(Random Finite Set,RFS)理论对说话人的个数和状态进行联合建模。最后,基于计算机仿真和实际的语料库对算法的性能进行了详细分析。
1 模型介绍
1.1 观测参数模型
在没有混响情况下的单个说话人场景中,麦克风对接收到的信号可以表示为[13]:
(1)
式中,s(t)为声源信号;vi(t),i=1,2为背景噪声;m为2个麦克风对之间的到达时间差(Time Difference of Arrival,TDOA)。采用二维坐标矢量α∈R2表示说话人的二维坐标(x,y)。则TDOA可以通过下面的计算获得:
(2)
式中,ui,i=1,2为麦克风的位置坐标;‖·‖表示距离;c表示声音的传播速度(实际上将这种方法可以直接扩展到三维坐标系中)。TDOA可以通过GCC估计其进行量测。其计算公式为[14]:
(3)
(4)


图1 实验中采用的断续语音信号Fig.1 Intermittent speech signal used in the experiment
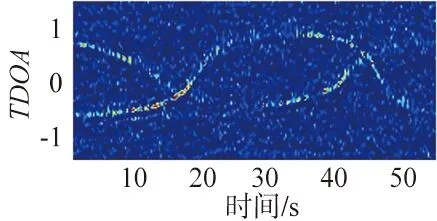
(a) 麦克风对1
在实际的说话人环境中,说话人的位置α是时变的。因此,需要采用一个适当短的时间帧来估计τ,目的是为了确保α在这个计算的时间帧上可以近似为静止不动的。本小节采用式(5)、式(6)的短时估计来代替式(4)中的Sy1,y2(w),其计算表达式为:
(5)
(6)
式中,T为短时的时间帧长度;k为短时的时间参数。
1.2 说话人运动状态的解相关分析
通过前面的研究可以看出,基于非线性滤波方法的说话人跟踪系统需要预先建立满足说话人运动特性的运动模型,多数研究采用朗之万模型,该模型的最大特点是满足说话人的随机运动特性。但是标准朗之万模型是在连续时间运动的基础上计算得到,但是实际应用中需要采用的是离散状态,其相应的离散化模型为:
x(k+1)=f(x(k))+w(k),
(7)
式中,x(k)∈Rn×1为说话人状态;f(·)为非线性状态函数传递过程;过程噪声w(k)为N(0,Q(k));其相应的观测模型为:
z(k)=g(x(k))+v(k),
(8)
式中,z(k)∈Rm×1为观测量;g(·)为相应的观测非线性函数;v(k)为满足N(0,R(k))的高斯噪声。假设上述系统满足噪声相关的条件,其相应的相关关系可以表示为:
(9)
假设跟踪目标的初始状态可以表示为x(0),其满足N(x0,P0)的高斯特性,且独立于w(k)和v(k)。在给定观测矩阵的情况下,相应的观测信息可以表示为:
(10)
过程噪声的离散值可以表示为:
(11)
相应的测量噪声矩阵可以表示为:
(12)
相应的方差可以计算为:
R(k)=E[v(k)vT(k)]=
(13)
式中,w(k)与v(k)的相关性为:
B(k)=E[w(k)vT(k)]=[B1(k),B2(k),…,BN(k)]。
(14)
因为R(k)为一个正定的实对称矩阵,故而存在酉矩阵U(k)满足:
Λ(k)=UT(k)R(k)U(k),
(15)
式中,Λ(k)=diag{λ1(k),λ2(k),…,λN(k)}为正定的对角阵;λj(k)(j=1,2,…,N)为R(k)的特征值,将U(k)左乘式(15),则有:

(16)
其中,
(17)
(18)
(19)
修正以后的测量噪声的统计特性可以表示为:
(20)
式中,Λ(k)=diag{Λ1(k),Λ2(k),…,ΛN(k)},这样就完成了测量噪声方差举证的解耦,而新的测量噪声与过程噪声之间的相关性可以表示为:
[C1(k),C2(k),…,CN(k)],
(21)
相应的状态方程可以改写为:

(22)
其中,
(23)
Q(k)-C(k)Λ-1(k)CT(k)。
(24)
上面分析的解耦以后的朗之万模型的状态空间方程可以重新表示为:
αk=αk-1+Tφk-1,
(25)
(26)
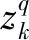
(27)
为了满足Cxk=αk,要求C=[I,0]。另外,真实计算的TDOA值为:
(28)
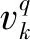
通过贝叶斯方法进行相应的递推估计说话人位置信息的后验概率密度函数可以表示为:
(29)
(30)
由于τq(·)的非线性,精确计算非常困难。目前研究中均采用蒙特卡罗近似处理的方法,也就是常说的粒子滤波方法。在进行相关解耦以后,需要将RFS方法引入到解耦以后的粒子滤波框架中进行未知数目的说话人跟踪处理。
2 基于解相关RFS的说话人跟踪
2.1 RFS框架内的滤波思想分析
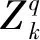
f(χk/χk-1),
(31)
似然函数可以表示为:
(32)

(33)
(34)
式中,F(Rn)为Rn所有有限子集的类;μ为F(Rn)的一个量测。
2.2 基于RFS-DPF的跟踪实现步骤
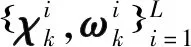
(35)

(36)
对于说话人的状态估计,结合贝叶斯递归公式可以表示为:
(37)
结合前面的分析,可以将基于解相关粒子滤波与随机有限集结合的说话人跟踪方法(RF-DSPF)的具体步骤总结如下:
对于k=1,2,…,N,给定粒子集合的总长度L,其具体的实现步骤:
① 噪声特性解相关
根据解相关步骤分析,针对系统噪声特性进行解相关分析,并获取解相关以后的系统状态方程:

和相应的量测方程:
获得解相关以后的说话人运动模型。
② 标准采样

③ 重采样

(38)
(Pmiss+(1-Pmiss)×
(39)
(40)
3 混响环境下仿真实验分析
该部分主要针对方法进行2类仿真实验:首先,针对提出的解耦相关粒子滤波方法和RFS相结合,进行了多说话人(2个不连续说话人)的计算机仿真实验;然后,针对AMI提供的智能会议环境中的语料库资料,采用本文方法,分别针对多人分开交互单人不连续发音、多人同时交互不连续发音的情况进行了仿真分析,并给出具体的实验分析结果。
3.1 混响环境下多人交互实验仿真分析
仿真分析中,参量设置如下:状态采用解相关分析中的朗之万运动模型,TDOA的标准偏离度误差为σv=124 μs(同样也是语音信号的采样周期)。其他的参量设置为:Nmax=1,Pbirth=0.05,Pdeath=0.01,Pmiss=0.25,λc=3,L=500。仿真实验分析主要针对实际量测的TDOA结果以及实际的说话人数目进行实时的测量和估计,验证本文方法针对多交互说话人的跟踪效果。图3展示了本例中房间的具体设置,房间大小为3 m×3 m×2.5 m。
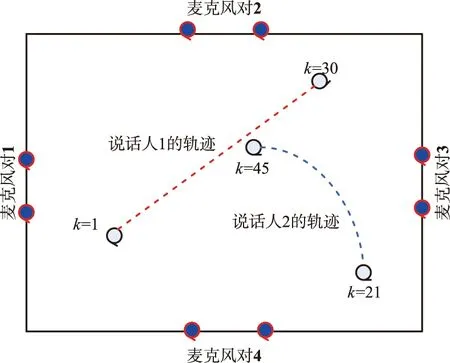
图3 仿真用的实验室布局及相应的说话人轨迹Fig.3 Laboratory layout and speaker trajectory for simulation
实验中采用4个麦克风进行语音信号采集,每对麦克风之间的距离为0.5 m(相互的时间延迟为1.5 ms),图中也给出了说话人的运动轨迹,以及说话人加入和消失的时刻。说话人的声音为一男一女,其中说话人1的语音信号如图1所示,说话人2的语音信号如图4所示。
图4 实验中采用的语音信号Fig.4 Speech signal used in the experiment
房间脉冲响应的混响时间为T60=0.15 s,为选择合适SNR进行跟踪分析,针对不同SNR情况下跟踪精度进行了分析,跟踪误差值如图5所示。从中可以看出,随着SNR的增加跟踪精度也在改善,但是改善的效果明显降低,结合实际环境中SNR的状态,本文信噪比取值为SNR=20 dB,量测的TDOA的时间帧长度为128 ms,时间上的交互是不重叠的。

图5 不同SNR情况下跟踪误差值Fig.5 Tracking error under different SNR conditions
4个麦克风对在整个时间段内的TDOA量测信息如图6所示。
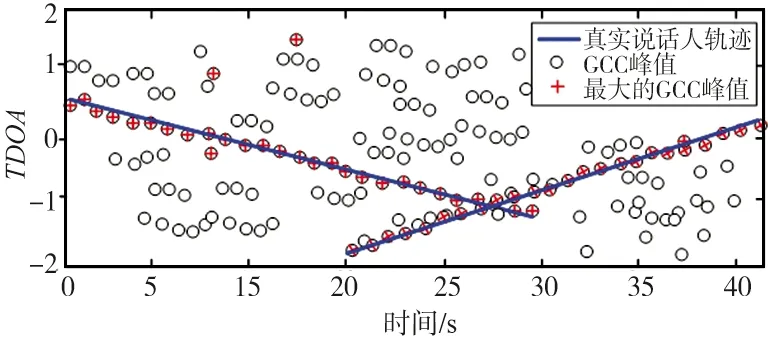
(a) 麦克风对1获取的TDOA估计
由图6可以看出,量测值出现了很多虚假的峰值信息,GCC的最大值并不是一直表示着真实的TDOA值。而且,在20~30 s之间,由于2个人同时说话,相互之间语音信号干扰,导致TDOA量测出现了较大的恶化。本文方法对说话人数目的实时估计效果如图7所示,可以看出,估计是有效的。

图7 说话人个数估计效果Fig.7 Results of speaker number estimation
3.2 混响环境下多人交互语料库仿真分析
该部分主要是针对AMI提供的智能会议环境下的标准语料库信息进行实际环境的实验仿真分析,其中,语料库信息采集的智能会议布局如图8所示。针对该语料库信息,该部分主要做了2组仿真分析实验。第1组,主要是针对多人交互发言,但每一次只有一个人发言情况下的说话人进行跟踪;第2组,主要针对2个人交互,但有时同时发言、有时同时静默的情况进行定位跟踪具体的实验结果如图9~图12所示。

图8 AMI智能环境布局Fig.8 Layout of AMI intelligent environment
图9给出了第一组单人不重叠交互的跟踪结果图。
由图9可以看出,该段语料库是一种有4个人参与会议的讨论,但是真正参与讨论的人有2个,这2个人轮流发言,彼此说话在时间域不存在重叠现象。跟踪结果显示,本文方法保持了较好的跟踪精度。在单人交互不重叠发言的情况下,2种方法均保持了满足要求的跟踪定位结果。

图9 单人交互发言的跟踪结果Fig.9 Tracking results of single person interactive speaking
目标位置跟踪的坐标均方误差值如图10所示,RFS-PF为随机有限集-标准粒子滤波方法跟踪结果(在图中以黄色椭圆标记跟踪结果),RFS-DPF为随机有限集-解耦粒子滤波跟踪结果(在图中以红色椭圆标记跟踪结果。)

(a) x轴位置均方误差曲线
由图10可以看出,在这种简单交互场景下位置跟踪均方误差为0.03和0.2,精度较高,主要原因是在这种简单的交互环境下,不存在交互重叠现象,噪声之间的相关性影响较小,所以2种方法的跟踪效果基本保持一致。
由图11可以看出,当说话人在时间上具有重叠性的时候,彼此之间的模型噪声关联性增强,如果不加入解相关处理的话,会导致跟踪误差累积效应明显增加。

图11 多人重叠交互发言的跟踪效果Fig.11 Tracking results of multi-person overlapping interactive speaking

(a) x轴位置均方误差曲线
由图12的跟踪均方误差曲线可以看出,加入解相关处理以后,跟踪误差保持稳定,没有出现较大的波动,特别是在说话人语音重叠的时候,仍然保持了很好的跟踪效果。
4 结束语
针对说话人存在场景下,说话人不连续发音以及说话人之间的交互说话问题进行了分析研究,提出了采用随机有限集思想,将多个目标的多种状态建立为随机的有限集合,分别作为系统模型的单一状态;为处理说话人语音重叠情况的跟踪效果,将模型噪声进行解相关处理,保证在语音重叠情况下系统模型的相互独立性,增强了系统的跟踪稳定性和跟踪精度。最后,将解相关噪声粒子滤波方法引入到了RFS理论框架,给出了相应的应用框架结构,并基于计算机仿真和实际的AMI语料库对不同场景下的多说话人定位跟踪效果进行了仿真分析,实验结果证明了本文所提方法的可行性和优越性。
