一种组稀疏高阶变分的图像复原模型
2021-09-07陈明举熊兴中张劲松杨志文
王 鸿,陈明举,熊兴中,张劲松,杨志文
(1.四川轻化工大学 人工智能四川省重点实验室,四川 宜宾 644000;2.四川轻化工大学 自动化与信息工程学院,四川 宜宾 644000)
0 引言
从退化图像中复原出真实的图像是一个不可逆的病态问题,基于图像梯度正则化的变分技术能在实现图像复原的同时增强图像的细节信息,获得较好的图像复原性能[1-2]。然而,在图像的平滑区域,变分技术会误将噪声当作图像的细节进行增强,从而产生阶梯现象[3],其图像复原性能有限。为了有效消除变分模型的阶梯现象,一些学者利用高阶梯度能有效区分噪声强度的特点,将图像的高阶梯度作为变分模型的正则化项,提出了一些高阶变分图像复原模型,例如拉普拉斯高阶变分模型[4]、基于四阶梯度的变分模型[5]以及增强高阶非凸全变分模型[6]等。高阶变分模型在增强图像边界的同时,有效减弱阶梯现象,但高阶梯度忽略了图像弱纹理与细节信息,造成图像部分细节信息的模糊[7]。为有效利用低阶变分与高阶变分的优点,一些学者建立低阶梯度与高阶梯度相结合的正则化变分模型[8-9],通过调节低阶梯度与高阶梯度权重,有效地实现图像边界与细节信息的增强,但该变分模型仍然基于图像的梯度信息,不可避免地在图像平滑区域产生阶梯现象[10],图像复原性能有限。
另一方面,一些学者将稀疏技术引入到变分模型,对变分模型的正则化项加以稀疏限制,利用图像的稀疏性与自相似性实现图像信息的重构[11],从而减弱了图像平滑区域阶梯现象的产生,例如基于稀疏限制变分模型(Sparse Total Variation,STV)[12]、低秩稀疏变分模型(TV Regularized Low-Rank Matrix,LRTV)[13]以及组稀疏变分模型(Group Sparse Total Variation,GSTV)[14]等。研究表明,与稀疏技术相比,组稀疏技术不仅实现图像的稀疏表示,更能体现图像中隐藏的结构相似性[15-16],若将组稀疏技术应用于高阶变分模型中,势必进一步提高变分技术的图像修复性能。
为了更好地利用图像的稀疏性与结构相似性,建立更有效的正则化图像复原变分模型,本文将组稀疏技术引入到高阶变分模型中,建立一种非凸的组稀疏高阶变分模型(Group Sparse Higher-order Total Variation,GSHOTV),并将迭代修正权值l1方法与极小化最大值算法引入到交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)中,以实现该非凸性组稀疏高阶变分模型的优化求解。
1 组稀疏高阶变分模型
1.1 组稀疏高阶变分模型的建立
为减弱基于一阶梯度l1范数变分模型的阶梯现象,并同时增强图像的边界,Bredies等人[4]将二阶梯度作为正则化项,建立自适应lp(0 (1) 式中,f为退化图像;K为线性退化函数;u为真实图像;0<ω为正则化参数;ϑc(u)为特征函数,以确保HOTV存在极点,其取值为: (2) 式中,C为图像像素值取值范围。由于HOTV采用lp范数的非凸性,Lyu等人[17-18]引入迭代修正权值l1算法(Iterative Re-weightedl1Algorithm,IRL1)将lp范数变分模型转换为l1范数变分模型,通过IRL1实现HOTV的迭代求解的方程为: (3) 式中,权值参数ω的更新为: (4) 式中,τ为接近0的正数。HOTV采用二阶梯度增强图像的边界,减弱了平滑区域阶梯现象的产生,但同时模糊了图像部分较弱的细节信息。 组稀疏技术利用自然图像相似的图像块在稀疏系数分布上更相近或相似的特性,对相似的稀疏系数进行分组,从而更多地考虑图像的结构相似性,以更好地重构图像的结构与纹理信息。为提高正则化变分技术的图像复原性能,Liu等人[14]将组稀疏技术引入到变分模型中,建立GSTV模型: (5) 式中,Du表示图像u的梯度;φ(u)表示对u的组稀疏表示: (6) 对于GSTV模型的求解,可以采用收敛性较快的极小化极大值迭代(Majorization Minimization,MM)进行求解[19],其极小化优化迭代求解u迭代步骤为: (7) 式中,Λ为对角矩阵;对角值Λ(u)n,n为: (8) 图像的平滑区域通常存在自相似性,组稀疏技术利用图像的自相似性实现图像平滑区域的重构,从而克服阶梯现象的产生。对于图像的孤立区域,无法找到相似信息对其进行重构,GSTV模型会造成孤立区域模糊[20]。 为有效利用高阶变分增强图像边界、组稀疏变分重构图像相似信息的优点,在自适应范数的二阶变分模型基础上,对图像一阶梯度进行组稀疏限制,建立一种GSHOTV,以便获得更好的图像复原性能,建立的GSHOTV为: (9) 交替方向乘子法结合对偶法的可分解性与高效收敛性,在多变量范数的凸优化中表现出较好的稳定性与收敛性[21-22]。另一方面,GSHOTV模型中涉及到u,u与2u多个变量的求解,可以采用ADMM方法分解成各个变量的子问题,进而引入IRL1与MM算法对子问题的优化求解,最终实现GSHOTV模型的求解。 引入ADMM辅助参量v,w与z三个参数,GSHOTV模型可进一步转换为: (10) 其对应的拉格朗日方程为: (11) 式中,μ1,μ2,μ3为拉格朗日参数;ρ为逼近算子。 GSHOTV模型的极小化求解可以分解成u,v,w与z三个子问题的求解。 u的子问题为: (12) 通过梯度极小化可以实现u的求解: uk+1=(λKTK+ρT+ρ(2)T2+ρI)-1· (λKTf-Tμ1+ρTv-(2)Tμ2+ρ(2)Tw+ρz), (13) 式中,KTK,T与(2)T为BBCD循环矩阵,若直接计算出各循环矩阵的值,计算量较大。由于循环矩阵可以表示为正逆傅里叶变换矩阵与傅里叶变换系数矩阵相乘的形式[23]。因此,通过2FFT求出BCCB矩阵特征值矩阵,再与正交矩阵相乘,从而实现BCCB矩阵的快速求解[24]。 v的子问题为: (14) v的极小化问题实质上是一个GSTV模型,采用极小化极大值MM迭代进行求解可进一步转化为: (15) w的子问题可以引入IRL1方法,转化为: (16) 式中,ti为权重参数,其值为: (17) w的极小化可以通过阈值收缩得到: (18) z的极小化问题: (19) 上述极小化问题可以进一步转换为: (20) zk+1可以通过下式求得: (21) 拉格朗日乘子可以通过下列算子更新: (22) (23) (24) 综上分析,GSHOTV模型采用引入IRL1与MM算法的ADMM优化求解过程如下: GSHOTV模型ADMM优化求解步骤初始化:u0=f,μ01=μ02=μ03,λ=ρ=0.01,ω=0.1,k=1;While‖uk-uk-1‖2/‖uk‖2>ERR按式(13)更新uk+1;按式(15)更新vk+1;按式(18)更新wk+1;按式(19)更新zk+1;按式(22)~式(24),分别更新拉格朗日乘子μk+11,μk+12与μk+13;k=k+1;endwhile 为证明本文提出的组稀疏高阶变分模型GSHOTV图像复原的性能,将GSHOTV模型修复后的结果与HOTV、GSTV模型修复的结果进行对比。实验中退化函数K分别选取均值退化、高斯退化与运动退化,均值退化与高斯退化模板hsize大小设置7×7,运动退化的尺度len设置为9,方向为水平;加性噪声为高斯噪声,方差为σn。采用测试的部分图像如图1所示,其性能的客观指标采用峰值信噪比(Peak Signal to Noise Ratio,PSNR)和结构相似性(Structral Similarity Index,SSIM)如表1所示。 (a) 女生 表1 不同退化图片采用3种模型复原后性能比较(PSNR,SSIM)Tab.1 Restoration results of different models based on different degraded images (PSNR,SSIM) 图1中,图像采用不同方式进行退化模糊,再分别采用3种模型实现图像的复原。从表1中可以看出,本文的GSHOTV图像复原模型获得最高的PSNR与SSIM。与HOTV结果相比,GSHOTV的PSNR提高约0.3~1.5 dB。表1数据说明,本文的GSHOTV模型将组稀疏技术与高阶变分相结合,消除了阶梯效应的影响,同时保留高阶变分增强图像边界的优点,复原后的图像更接近原始图像。 为分析本文GSHOTV模型的收敛性能,将迭代停止条件设置为ERR≤0.01,分别记录3种模型达到收敛时的运行时间t与迭代次数k。表2给出“女生”图像在不同退化情况下,采用3种模型复原所花的时间与迭代次数。 表2 女生图像在不同退化环境采用3种复原模型运行时间分析Tab.2 Operation time of different models based on different degraded girl image 从表2数据可以看出,本文的GSHOTV模型耗时与迭代次数远低于GSTV模型,其迭代次数和运算时间与HOTV相当,说明将IRL1与MM算法引入到ADMM迭代中,可以高效实现GSHOTV模型的求解。在主观评价方面,分别对3种模型实现复原后的图像结构与细节信息进行对比分析。为便于观察,图2与图3分别给出了平滑图像“Woman”在高斯退化下(hsize=9×9,σn=20)与强纹理图像“Zoneplate”在移动退化下(len=9,σn=30),采用3种模型复原后的结果与差值图像。 (a) 原真实图 (a) 原真实图 从图2和图3可以看出,HOTV有效地增强了图像的边界,但把平滑区域的部分噪声当作边界实现了增强,从而产生阶梯现象;GSTV虽然有效减弱了平滑区域的阶梯现象,但模糊图像的部分边界与细节;本文提出的GSHOTV模型差值图像灰度值最小,不仅有效地克服了平滑区域阶梯现象的产生,且更好地复原图像的细节信息。图2和图3实验说明,GSHOTV模型中组稀疏项有效地利用图像相似信息实现平滑区域与相似细节的重构,同时高阶变分项实现图像细节的增强,从而获得更好的图像复原性能。 为了进一步从主观上说明GSHOTV模型具有更好的图像修复性能,图4~图7给出图1中4幅图像在不同退化情况下的复原后的图像,为便于对比复原的效果,在各个图的右上角给出绿色区域的放大图。 (a) 移动退化图像 (a) 均值退化图像 (a) 均值退化图像 (a) 运动退化图像 从图4~图7可以看出,HOTV模型较好地复原了图像的边界,但在平滑区域存在阶梯效应;GSTV模型较好地去除图像的干扰噪声与阶梯现象,但同时模糊了图像的细节;本文的GSHOTV模型在实现图像干扰消除的同时,更好地复原与增强了图像的纹理与细节信息,如“女生”图片中的橘子纹理、“蝴蝶”图像中的斑点、“水果”图像中花纹以及“汽车”图像中的车标信息都较好地实现了复原。以上分析再次说明,本文的GSHOTV模型中的组稀疏项有效利用图像的相似信息消除阶梯现象,高阶变分项增强图像的细节信息,从而获得更好的图像复原性能。 针对变分模型在图像复原中的性能进行相应的分析,低阶变分和高阶变分有各自的优缺点,将二者相结合的正则化变分模型,在复原性能上也有局限性,为了更好地实现图像信息的复原并增强图像的纹理结构信息,将图像表示的组稀疏技术引入到高阶变分模型中,能提高变分技术的图像修复性能,建立一种非凸的组稀疏高阶变分模型,并将迭代修正权值l1算法与极小化最大值的方法引入到交替方向乘子法中,实现建立的非凸的组稀疏高阶变分模型的优化求解。通过对比实验,证明本文提出的非凸的组稀疏高阶变分模型有效地复原图像的细节与纹理信息,消除了阶梯现象,获得更好的图像复原效果,使变分技术的图像修复性能进一步提高。因此,本文提出的组稀疏高阶变分图像复原模型具有很好的应用前景。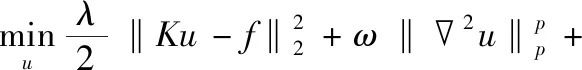

1.2 组稀疏高阶变分模型的求解
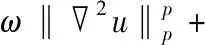
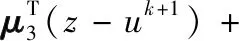


2 结果与讨论









3 结束语
