一道解析几何模拟试题的探究及溯源

广东省中山市濠头中学(528437) 闫 伟

圆锥曲线与直线的位置关系一直是高考的热点和难点,在很多圆锥曲线题目中都是探求一些特殊结论,如定值问题,这些结论看似特殊,实则具有普遍性,且往往具有丰富的命题背景和深厚的内涵,研究此类试题不仅能够更好地把握解析几何的本质,还能透过试题挖掘隐含的命题规律,更能将其拓展到一般情况,从而提升学生数学思维,发展数学核心素养.下面以2021年北京市丰台区模拟考试解析几何试题为例进行说明.

1 试题呈现与分析

题目(2021年北京丰台区模拟)已知椭圆1(a ＞b ＞0)过A(0,2),B(-3,-1)两点.

(1)求椭圆E的方程;

(2)直线AB与x轴交于点M(m,0),过点M作不垂直于坐标轴且与AB不重合的直线l,l与椭圆E交于C,D两点,直线AC,BD分别交直线x=m于点P,Q,求证:为定值.

分析本题主要考查对椭圆的标准方程及其几何性质、直线与椭圆的位置关系、韦达定理、线段长度定值等基础知识的理解和运用,考查学生的推理论证能力、运算求解能力以及综合运用所学知识分析问题和解决问题的能力,侧重考查数形结合、化归与转化的思想.试题梯度明显,既能让绝大多数考生有所收获,又能区分不同层次的学生,下面着重探讨第二问.第二问要证明的线段PM和MQ的比值,解决思路是联立直线l与椭圆方程,利用C,D两点坐标分别表示两个线段长度,再结合韦达定理运算求解.本题立意深刻、内涵丰富,具有一定的典型性、代表性,极具探究价值,是一道值得研究的好题.

2 解法探究

解答(1)椭圆E的方程为= 1,过程从略;以下考虑(2)的解答.

解法1依题意知m=-2, 设直线l方程y=k(x+2)(k /= 0,1),C(x1,y1),D(x2,y2), 直线与椭圆联立:得(3k2+1)x2+12k2x+12k2-12=0,且Δ＞0,则x1+x2=记直线AC方程为:y=+2,又点P在直线AC上,当x=-2 时,得点P的纵坐标yP=同理可求得点Q的纵坐标为yQ=从而

评注本解法要解决线段长度比值, 先联立l与E的方程并借助韦达定理求解, 设出点C,D的坐标并表示点P,Q的纵坐标, 难点是这一不对称形式让学生不知所措,实际上是要结合三个参数k,x1,x2的等量关系进行配凑,然后通过代数恒等变形消参数求得定值,解题思路较为常规,只是运算量较大,要求学生具备较强的数学运算、逻辑推理能力.

解法2由m=-2,设C(x1,y1),D(x2,y2),直线l:x=ty-2 与椭圆联立:=1 得: (t2+3)y2-4ty-8=0且Δ＞0,则y1+y2=,y1y2=-记直线AC方程为:y=+2,又点P在直线AC上,当x=-2时,得点P的纵坐标yP=同理可求得点Q的纵坐标为yQ=从而

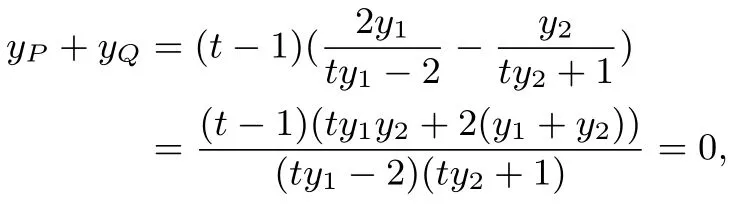
评注解法2 通过直线方程的另一种方式与椭圆联立,结合韦达定理求解;另外将几何结论代数化,即利用点P,Q的纵坐标互为相反数求解定值,极大简化求解过程,实现高效解题.

3 基于GeoGebra 的探究与反思

通过对试题的分析和解答, 笔者在想这两条段长度比值为定值1(即两线段相等)是必然还是偶然呢? 怎样透过现象看本质, 揭示问题的一般性规律? 数学家波利亚曾说过: 先猜,后证——这是大多数发现之道.于是笔者试着换了一个点M′(-1,0),过点M′作两条不垂直于坐标轴的直线AB,CD,直线AC,BD分别与x=-1 交于P,Q两点,P,Q两点的纵坐标仍然互为相反数;再换一些特殊点M重复上述操作过程,结论仍成立.笔者猜想: 当点M(m,0)与直线l:x=m存在某种联系时,两线段长度恒相等,于是笔者通过借助GeoGebra 平台进行探究验证.通过实验来验证上述变量间的关系,同时为后面的代数证明提供更加直观形象的思路支持.

实验(1)在GeoGebra 绘图区先设置两个“滑动条”a,b, 输入:x^2/a^2+y^2/b^2=1,得到椭圆C; (2)在工具栏设置“滑动条”m,输入点M(m,0)(m /=±a),并输入直线x=m;(3)过点M作两条不垂直于坐标轴的直线分别与椭圆交于A,B,C,D,记直线AC,BD分别与x=m交于P,Q两点;(5)拖动M点,或者改变参数a,b的值,进行演示,如图1.

图1

根据上述演示结果,我们可以将结论推广到更一般的情况:

4 推广结论 揭示本质

结论1已知椭圆E:= 1(a ＞b ＞0),过点M(m,0)(m /=±a)作两条不垂直于坐标轴的直线分别与椭圆交于A,B,C,D, 记直线AC,BD分别与直线l:x=m交于P,Q两点;则|PM|=|MQ|.

证明平移直角坐标系, 将坐标原点O平移到点M得到坐标系x′My′, 记椭圆与y′轴交于H,G两点, 显然MG=MH, 不妨设H(0,t),G(0,-t),P(0,y′P),Q(0,y′Q),因为椭圆过H,G两点, 故可设平移后的椭圆方程为ux′2+y′2+vx′y′+wx′-t2=0,另设直线AB,CD的方程分别为y′=k1x′,y′=k2x′,从而过点A,B,C,D的曲线系方程为ux′2+y′2+vx′y′+wx′-t2+λ(y′-k1x′)(y′-k2x′)=0,其中λ ∈R,令x′=0,则y′P,y′Q是方程(1+λ)y′2-t2=0的两根,由根与系数关系可知y′P+y′Q=0,所以在平移后的坐标系中有|PM|=|MQ|,因平移坐标系不改变线段的长度,从而|PM|=|MQ|.

评注上述结论1 同样适用于双曲线和抛物线,证明过程和结论1 相仿,此处不再赘述.

结论2已知双曲线E:= 1(a ＞0,b ＞0),过点M(m,0)(m /=±a)作两条不垂直于坐标轴的直线分别与双曲线交于A,B,C,D, 记直线AC,BD分别与直线l:x=m交于P,Q两点,则|PM|=|MQ|.

结论3已知抛物线E:y2= 2px(p ＞0), 过点M(m,0)(m /= 0)作两条不垂直于坐标轴的直线分别与抛物线交于A,B,C,D, 记直线AC,BD分别与直线l:x=m交于P,Q两点,则|PM|=|MQ|.

5 背景探寻 追根溯源

至此,对上述题目基本结论的探究告一段落.但我们仍有疑问,为什么有这些结论呢? 这些结论的源头在哪里? 我们知道,椭圆与圆有着紧密的联系,它们具有许多相似的性质.我们不妨来考查圆中的结论,借助圆来探究一下这道题的背景.

结论4已知点M是⊙O外一点, 过点M作OM的垂线l, 过点M且不垂直于l的两条直线分别与圆交于A,B,C,D四点,记直线AC,BD分别与直线l交于P,Q两点,则|PM|=|MQ|.

证明如图2, 过圆心O作AC,BD的 垂 线, 垂足分别为F,E, 则F,E分别为弦AC,BD中点; 连接OP,OQ,MF,ME, 因为OM⊥PQ, 所 以O,F,M,P四点共圆,O,E,M,Q四点共圆, 于是∠POM= ∠PFM,∠QOM= ∠QEM; 因 为∠MCA= ∠MBD, 所 以ΔMAC∽ΔMDB, 故有结合∠MCF= ∠MBE得ΔMCF∽ ΔMBE, 于是∠MFC=∠MEB,所以180°-∠MFC=180°-∠MEB,即∠PFM= ∠QEM; 故∠OPM= 90° -∠POM=90°-∠PFM=90°-∠QEM=90°-∠QOM=∠OQM,即点M是PQ中点,故|PM|=|MQ|.

图2

至此,我们通过探究得到了圆中具一般意义的结果.但是对于圆成立的结论是如何推广到椭圆中去的? 事实上,椭圆可以由圆经过伸缩变换得到,由伸缩变换的性质——保持点线结合关系不变、直线平行或相交关系不变、同一直线上线段长的比例关系不变等.可知上述结论4 对于椭圆仍然成立.事实上,这也完成了结论1 的一次简洁的证明.

根据圆的一般结论分析,上述结论1-3 中的点M和直线l:x=m仍然比较特殊,能否将其一般化呢? 即点M为不在椭圆上的任意一点,此时直线l需满足什么要去才能保证上述结论仍然成立? 结合高等几何中极点极线的相关知识,笔者借助GeoGebra 平台继续探究得到圆锥曲线中更一般性的结论.

结论5已知点M是不在椭圆E:= 1(a ＞b ＞0)上的任意一点,点M关于椭圆E的极线为直线m,记过点M且平行于直线m的直线为l,过点M作两条不重合的直线分别与椭圆E交于A,B,C,D,记直线AC,BD分别与直线l交于P,Q两点;则|PM|=|MQ|.

结论6已知点M是不在双曲线E:= 1(a ＞0,b ＞0)上的任意一点, 点M关于双曲线E的极线为直线m,记过点M且平行于直线m的直线为l,过点M作两条不重合的直线分别与双曲线E交于A,B,C,D, 记直线AC,BD分别与直线l交于P,Q两点;则|PM|=|MQ|.

结论7已知点M是不在抛物线E:y2= 2px(p ＞0)上的任意一点,点M关于抛物线E的极线为直线m,记过点M且平行于直线m的直线为l,过点M作两条不重合的直线分别与抛物线E交于A,B,C,D,记直线AC,BD分别与直线l交于P,Q两点;则|PM|=|MQ|.

结论5-7 的证明需要借助高等几何中极点极线的相关结论,留给有兴趣的读者,此处不再一一赘述;根据极点和极线的性质,我们将结论5-7 统一概括为:

结论8已知点M是不在圆锥曲线E上的任意一点,点M关于曲线E的极线为直线m,记过点M且平行于直线m的直线为l,过点M作两条不重合的直线分别与曲线E交于A,B,C,D,记直线AC,BD分别与直线l交于P,Q两点;则|PM|=|MQ|.

极点与极线是解析几何中的一条重要性质,它在圆锥曲线问题的探究中有十分重要的应用,本文对这一类定值问题的探究很好地佐证了这一点.

结束语

以上由一道试题出发,经过特殊到一般,得到了圆锥曲线中一组统一的性质.在解题教学过程中,我们不能仅仅停留在问题的表面,还要引导学生深入理解学科知识的本质特征和内在联系,对经典题目进行抽丝剥茧,从不同角度联想与探究,尽可能地将试题的研究价值最大化,从而提升学生的数学核心素养.