利用导数证明不等式的五种常用策略

安徽省太湖中学(246400)李昭平

近几年的高考和模考, 出现了不少证明不等式的问题,旨在加大导数运用的推理论证力度, 凸显了对数学的灵魂“推理”的高度重视.下面选择典型考题,介绍导数证明不等式的五种常用策略,供参考.

策略1 差值函数法

例1(2021年皖江联盟开年考题)已知函数f(x)=lnx+ax2-x,其中a≥0.

(Ⅰ)讨论f(x)的单调性;

(Ⅱ)若函数g(x)=f(x)+ex+(1-a)x2-lnx,证明:当x ＞0 时,g(x)＞+1.

思路作差g(x)--1, 构造新函数h(x)=g(x)--1,研究新函数h(x)的单调性.

解析(Ⅰ)f′(x)=+2ax-1=,x ＞0.若a=0,f′(x)=-,f(x)在(0,1)内单增,在(1,+∞)内单减.若a ＞0,由2ax2-x+1 = 0 知,Δ = 1-8a.当Δ = 1-8a≤0,即a≥时,2ax2-x+1 ≥0,此时f(x)在(0,+∞)内单增.当Δ = 1-8a ＞0,即0＜a ＜时,此时f(x)在

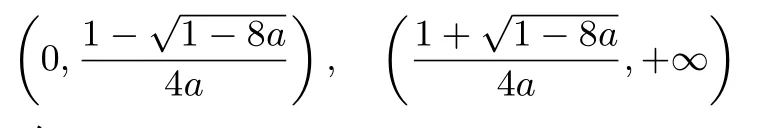
内单增,在内单减.

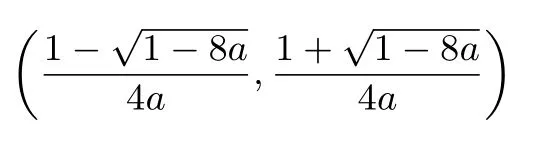
(Ⅱ)因为g(x)=f(x)+ex+(1-a)x2-lnx=ex+x2-x,所以g(x)＞+1 就是ex+x2-x ＞+1,即ex+x2-x--1＞0.令h(x)=ex+x2-x--1,x ＞0,则h′(x)=ex+2x-1-,x ＞0,h′′(x)=ex+2-3x,x ＞0.由h′′′(x)= ex -3 = 0 得,x= ln 3,h′′(ln 3)是h′′(x)的最小值.于是h′′(x)≥h′′(ln 3)=5-3 ln 3＞0,h′(x)在x ＞0时单增,所以h′(x)＞h′(0)=0,h(x)在x ＞0 时单增.故当x ＞0 时,h(x)＞h(0)=0,即g(x)＞

例2(2020年青岛模考题)若函数f(x)=x-sⅰnx.证明: 当x ∈[0,π],θ ∈(0,π)时,

思路作差构造新函数研究新函数g(x)的单调性.

解析

令g(x)=则g′(x)=-cosx).因为x ∈[0,π],θ ∈(0,π),∈(0,π), 而cosx在[0,π] 内单减,所以由g′(x)=-cosx)= 0 得,x=θ.当θ ＜x≤π时,g′(x)＞0,g(x)单增; 当0 ≤x ＜θ时,g′(x)＜0,g(x)单减.因此g(θ)是g(x)在[0,π]上的最小值.于是g(x)≥g(θ)=0,≥0,即当x ∈[0,π],θ ∈(0,π)时,成立.

评注例1 中构造新函数g(x)= ex+x2-x-1,x≥0,并三次求导数,利用g′′′(x)的最值确定g′′(x)的符号,再利用g′′(x)的符号确定g′(x)的符号,进一步确定g(x)的单调性,从而证出不等式.例2 中待证的不等式中有参数θ,所以处理起来运算和思维的难度较大.也可以反客为主,视θ为主元、x为参数来处理.一般地, 运用差值函数法证明形如A(x)＞B(x)的不等式,主要步骤是: ①构造新函数h(x)=A(x)-B(x); ②求导h′(x)=A′(x)-B′(x); ③研究函数h(x)的单调性、极值、图象等(无法进行时,继续求导h′′(x)=A′′(x)-B′′(x), 研究h′(x)的单调性、极值、图象等); ④通过h′(x)或h′′(x),获得h(x)的性质,进而实现证明不等式A(x)＞B(x)的目标[1].

策略2 特征分析放缩法

例3(2019年安徽省A10 联盟联考题)设k ∈R,函数f(x)=(x-1)ex-其中e 是自然对数的底数.

(Ⅰ)若k=-1,求曲线y=f(x)在点(2,f(2))处的切线方程;

(Ⅱ)证明: 当k ＞1 时, 存在x0∈(lnk,+∞), 使f(x0)＞0.

思路对(Ⅰ),先求f′(2),再根据y-f(x0)=f′(x0)(x-x0)写出切线方程;对(Ⅱ),先证明ex ＞x2(x ＞0),再利用这个不等式对f(x)=(x-1)ex-进行局部放缩.

解析(Ⅰ)y=2(e2+1)x-3e2-2.过程从略.

(Ⅱ)先证当x ＞0 时,ex ＞x2.令g(x)=ex-x2,x ＞0,则g′(x)= ex-2x,g′′(x)= ex-2.由g′′(x)= ex-2 = 0得,x= ln 2,g′(x)≥g′(ln 2)= 2-2 ln 2＞0,g(x)＞g(0)= 1＞0, 故ex ＞ x2.于是当x ＞1 时, 有f(x)=(x-1)ex-取x0=k+1,k+1＞k-1＞lnk(k ＞1)且x0-k+1-＞0,使f(x0)＞0.故当k ＞1 时,存在x0∈(lnk,+∞),使f(x0)＞0.

例4(2021年南师大附中段考题)已知函数f(x)=ax2-2 lnx(a ∈R),f′(1)≥0.

证明当x ∈(0,2)时,＞0恒成立.

思路先确定参数a的取值范围,再利用这个范围对不等式进行消元放缩.

解析因为f′(x)=所以f′(1)= 2a-2 ≥0,a≥1,于是

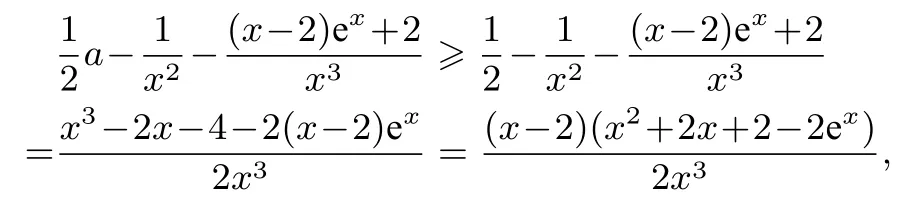
令h(x)=x2+2x+2-2ex,0＜x ＜2,则h′(x)=2x+2-2ex=2(x+1-ex).再令φ(x)=x+1-ex,则当x ＞0时,φ′(x)=1-ex ＜0,φ(x)单减,φ(x)＜φ(0)=0.因此当x ＞0 时,h(x)单减,h(x)＜h(0)=0 即x2+2x+2-2ex ＜0.于是当0＜x ＜2 时,＞0,故当x ∈(0,2)时,＞0 恒成立.

评注例3 以幂函数和指数函数的复合形式为载体,考查导数的几何意义和不等式问题, 融函数的单调性、最值、放缩等知识于一体, 有一定的难度.在“找点”中,运用不等式ex ＞x2(x ＞0)进行局部放缩是证明的关键.例4 要证明的不等式问题中含有参数a, 自然想到消去a, 变成证明关于x的不等式恒成立问题.利用a≥1 进行消元放缩得到对符号的判断,有变形的难度、运算的难度和构造的难度.局部放缩和消元放缩也是证明不等式的一种重要途径.

策略3 切线放缩法

例5(2021年三亚高二段考题)已知函数f(x)=xe3x-lnx-1.证明: 对任意实数x ＞0,都有f(x)＞2x恒成立.

思路变形xe3x= elnx+3x,利用ex≥x+1 切线放缩elnx+3x≥lnx+3x+1,往证f(x)＞2x.

解析因为ex≥x+1,所以elnx+3x≥lnx+3x+1.于是f(x)=elnx+3x-lnx-1 ≥lnx+3x+1-lnx-1=3x,当且仅当lnx+3x=0 时等号成立.因为x ＞0,所以3x ＞2x.故对任意实数x ＞0,都有f(x)＞2x恒成立.

例6(2021年南昌模考题)证明: 对任意x ＞0,ex-e2lnx ＞0 恒成立.

思路利用lnx≤x -1 切线放缩ex -e2lnx≥ex-e2(x-1),再证ex-e2(x-1)＞0.

解析因为lnx≤x -1(x ＞0), 所以-e2lnx≥-e2(x-1),当且仅当x=1 时等号成立.于是ex-e2lnx≥ex -e2(x -1), 当且仅当x= 1 时等号成立.令g(x)=ex -e2(x -1),x ＞0, 则g′(x)= ex -e2.当x ＞2 时,g′(x)＞0;当0＜x ＜2 时,g′(x)＜0.因此g(x)≥g(2)=0且ex -e2lnx≥ex -e2(x-1)≥0 中,两个等号不能同时成立.故对任意x ＞0,ex-e2lnx ＞0 恒成立.

例7(2021年哈尔滨八校联考题)设m ∈R, 函数f(x)=e2x-ln(2x-m).

(Ⅰ)设x= 0 是f(x)的极值点,求实数m的值,并讨论f(x)的单调性;

(Ⅱ)当m≥-2 时,证明:f(x)＞0.

思路对(Ⅰ),利用f′(0)=0 构建方程即可;对(Ⅱ),利用ex≥x+1 和lnx≤x-1 进行切线放缩.

解析(Ⅰ)m=-1,f(x)在内单减,在(0,+∞)内单增.过程略去.

(Ⅱ)因为e2x≥2x+1(当且仅当x= 0 时等号成立),-ln(2x-m)≥-(2x-m)+1(当且仅当时等号成立),所以e2x -ln(2x-m)≥2x+1-(2x-m)+1 = 2+m,当且仅当x= 0 且2x - m= 1 时等号成立, 即当且仅当m=-1 时等号成立.因为m≥-2, 当m /=-1 时,e2x -ln(2x-m)＞2+m≥0(2x-m ＞0); 当m=-1时, e2x -ln(2x+1)= 2+m= 1＞0(2x+1＞0).故当m≥-2 时,有f(x)＞0 恒成立.

评注直线y=x+1 是曲线y= ex在(0,1)处的切线, 且在曲线y= ex的下方, 所以有ex≥x+ 1(当且仅当x= 0 时等号成立)直线y=x -1 是曲线y= lnx在(1,0)处的切线, 且在曲线y= lnx的上方, 所以有lnx≤x -1(当且仅当x= 1 时等号成立).在证明相关不等式中,若能灵活运用这两个不等式进行切线放缩,往往事半功倍.一般的,有ef(x)≥f(x)+1,lng(x)≤g(x)-1 和eφ(x)-lnh(x)≥φ(x)-h(x)+2,扩大了应用的范围[2].

策略4 隔离分析最值法

例8(2020年安庆模考题)设a ∈R,证明: 当x≥1,a≥时,ax2-lnx+-e1-x -a≥0 恒成立(e = 2.718…,为自然对数的底数).

思路等价变形,一分为二成两个函数,分别确定两个函数的最值.

解析原不等式等价于ax2-lnx-a≥e1-x -即ax2-lnx-a≥令f(x)=ax2-lnx-a, 则f′(x)=2ax-当x≥1,a≥时,-1 ≥0, 所以f′(x)≥0.因此f(x)在[1,+∞)上单增,f(x)≥f(1)=0,f(x)mⅰn=0.再令g(x)=x-ex-1,则g′(x)= 1-ex-1≤0,g(x)在[1,+∞)上单减,g(x)≤g(1)=0,g(x)max=0.于是ax2-lnx-a≥恒成立,即ax2-lnx+-e1-x-a≥0 恒成立.

例9(2021年西安5 月段考题)设m≥函数f(x)=xlnx-mex.证明:f(x)＜0.

思路等价变形,一分为二成两个函数,分别确定两个函数的最值.

解析因为x ＞0,所以f(x)＜0 等价于令g(x)=则g′(x)=当0＜x ＜e 时,g′(x)＞0;当x ＞e 时,g′(x)＜0,所以g(x)max=g(e)=再令h(x)=则h′(x)=当0＜x ＜2时,h′(x)＜0;当x ＞2 时,h′(x)＞0,所以h(x)mⅰn=h(2)=因为m≥所以故即f(x)＜0.

评注例8 若像例1 那样直接构造函数h(x)=ax2-则其导函数h′(x)=2ax-非常复杂,无法确定h′(x)在x ∈[1,+∞)上的符号.无奈之时逼着我们另辟蹊径: 将此不等式“一分为二”成两个函数f(x)和则分别研究两个函数f(x)(过定点(1,0)的动曲线)和g(x)(定曲线)的最值即可.例9 则是隔离分析最值法的一种应用.一般地,证明h(x)=A(x)-B(x)≥0,当研究h(x)的单调性困难时,可以“一分为二”成A(x)≥B(x),考虑证A(x)mⅰn≥B(x)max是一种有效途径,往往称为隔离分析最值法[3].

策略5 换元法

例10(2019年广州5 月联考题)已知函数f(x)=x2+ax+blnx, 曲线y=f(x)在点处(1,f(1))的切线方程为y=2x.

(Ⅰ)求实数a和b的值;

(Ⅱ)设F(x)=f(x)- x2+mx(m ∈R),x1x2,(0＜x1＜x2)分 别 是 函 数F(x)的 两 个 零 点, 求 证:

思路对(Ⅰ),构建方程组即可;对(Ⅱ),利用等价变形和换元法处理.

解析(Ⅰ)易得a=1,b=-1.过程略去.

(Ⅱ)F(x)=f(x)-x2+mx=(x2+x-lnx)-x2+mx= (m+1)x -lnx.因为x1,x2(x1＜x2)分别是函数F(x)的两个零点, 所以两式相减, 得(m+1)(x1-x2)-(lnx1-lnx2)= 0, 所以m+ 1 =因为F′(x)=m+ 1-所以= (m+1)-要 证＞0, 即 证

因为0＜ x1＜ x2, 所以只要证lnx1-lnx2＜ ∈(0,1),则即证明lnt ＜.g(t)=lnt-,0＜t ＜1,则g′(t)=＞0,g(t)在(0,1)内单增.于是g(t)＜g(1)=0,即lnt ＜故＞0.

评注本题先将待证的不等式＞0 等价变形为＞0, 而此不等式中有两个字母参数x1,x2, 不好处理.继续将其等价变形为为新元t,通过换元,则问题立即化为关于t的一元不等式,利用差值函数法证明即可实现目标.

上述10 道例题,很好地体现了导数在整式函数、分式函数、三角函数、指数函数、对数函数以及它们的复合型函数不等式证明中的思想和方法.备考复习中要加大训练力度,逐渐把握相关策略.