基于PCA-GA-SVM的露天矿爆破振动速度预测模型研究

2021-09-06岳中文吴羽霄

工程爆破 2021年4期

岳中文,吴羽霄,魏正,王贵,王渊,李鑫

(1.中国矿业大学(北京)力学与建筑工程学院，北京 100083；2.内蒙古康宁爆破有限责任公司，内蒙古鄂尔多斯017010)

在工程爆破之前，准确预测和分析爆破振动峰值速度，进而优化爆破施工设计方案是有效减小爆破振动危害的主要方法[1]。然而影响爆破振动速度的因素众多，且各因素之间存在复杂的非线性关系，目前国内外学者用来预测爆破振动速度的主要方法有经验公式法[2-3]、BP神经网络[4-5]、多元非线性回归[6-7]等，但存在经验公式考虑因素较少、BP网络陷入局部最小值且收敛速度慢等问题。

基于以上现状，笔者提出建立基于PCA和GA算法优化支持向量机的爆破振动速度预测模型。支持向量机[8-10](SVM)作为一种新的机器学习算法，具有较强的全局寻优和小样本训练能力，能够解决爆破工程中样本少、非线性、影响因子多等实际问题。首先采用PCA对数据进行降维，提取影响爆破振动速度的主成分作为模型的输入变量，利用GA算法找到SVM模型的惩罚系数和核函数参数的最优参数组合，最终建立PCA-GA-SVM预测模型，同时与BP神经网络、传统SVM和GA-SVM模型对比，取得了良好的预测效果。

1 支持向量机(SVM)

支持向量机(Support Vector Machine，SVM)是Vapnik[11]等于1995年首次提出的一种新的机器学习方法，其基本原理是通过核函数在高维空间寻找最优分类超平面实现最优分类，解决低维样本非线性不可分问题。其中寻找最优分类超平面的优化函数为[11]

(1)

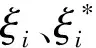
为求式(1)的最优解，引入拉格朗日乘子并建立Lagrange函数，将最优分类超平面转化为下列的对偶问题，即[11]

(2)

K(xi,x)=exp(-g‖x-xi‖2)

(3)

通过二次规划优化算法训练得到式(2)中最优的Lagrange乘子，最终得到的回归函数为[12]

(4)

2 基于PCA的GA-SVM模型建立

2.1 主成分分析(PCA)

主成分分析的原理就是利用Karhunen-Loeve变换[13]，计算原来变量的协方差矩阵并转化为对角矩阵，提取少数可以代表原始多维变量信息的低维且线性无关变量。主成分分析法可以完成数据的降维，提高模型处理数据的速度，其具体步骤如下：

1)将原始数据进行归一化处理，本文采用的是极差化归一化处理，公式如下：

(5)

式中：xi为待处理的样本数据；xmin为样本数据的最小值；xmax为样本数据的最大值;

2)设总体X有n个样本(X1,X2,…,Xn)，每个样本有m维变量，则观测数据的矩阵记为

3)将原始数据进行标准化，公式如下：

(6)

4)计算e=(e1,e2,…,en)T的相关系数矩阵，利用∑u=λu求出特征值λi和其特征向量ui。其中，λ1≥λ2≥…λm≥0；

5)通过计算得到的m个主成分，即[13]

(7)

其中，ui12+ui22+…+uin2=1(i=1,2,…,m)

2.2 遗传算法(GA)优化SVM关键参数

传统SVM算法对于惩罚系数c和核函数参数g的选取都是根据经验给定一个默认值，这对模型的预测精度有很大影响。遗传算法(Genetic Algorithm，GA)作为一种模拟生物界自然进化和自然遗传机制的现代启发式算法，具有全局搜索和全局优化的特点[14]，被广泛用于参数寻优问题。本文结合GA算法优化SVM的关键参数，采用实数编码方式将c和g进行编码，形成初代种群；选取预测值与实际值的误差平方和作为适应度函数。对任意样本集，其误差平方和越小，说明个体的适应度越好，其参加下一次迭代的机率越大；通过选择、交叉、变异运算，产生新一代适应度大的群体；不断重复迭代，直到达到最大迭代次数T，解码输出最优的参数组合。

综合以上原理，PCA-GA-SVM模型建立的实现流程如图1所示。

图1 PCA-GA-SVM模型实现流程Fig.1 Flow of PCA-GA-SVM model implementation

3 工程应用

3.1 模型样本选取及预处理

以内蒙古康宁爆破公司福强煤矿爆破工程为例，福强煤矿岩体强度平均值为6.40 MPa，岩石硬度系数为3。本工程采用深孔台阶松动爆破，台阶设计高度为10 m，钻孔方式采用垂直钻孔，布孔采用三角形布孔方式。结合爆破方案和现场实际情况，选取填塞长度X1(m)、高程差X2(m)、最大段药量X3(kg)、最小抵抗线X4(m)、孔深X5(m)、设计单耗X6(kgm-3)、孔距X7(m)、排距X8(m)和爆心距X9(m)作为影响爆破振动速度的因子，爆破振动速度的实测数据为Y。在爆破作业时，采用TC-4850爆破测振仪进行实时监测，共测得69组有效爆破测振数据进行模型的训练和预测，实测数据如表1所示。为使输入向量的数据量纲一致，首先通过式(5)对各影响因子的原始数据进行[-1,1]区间的归一化处理，处理后的数据如表2所示。

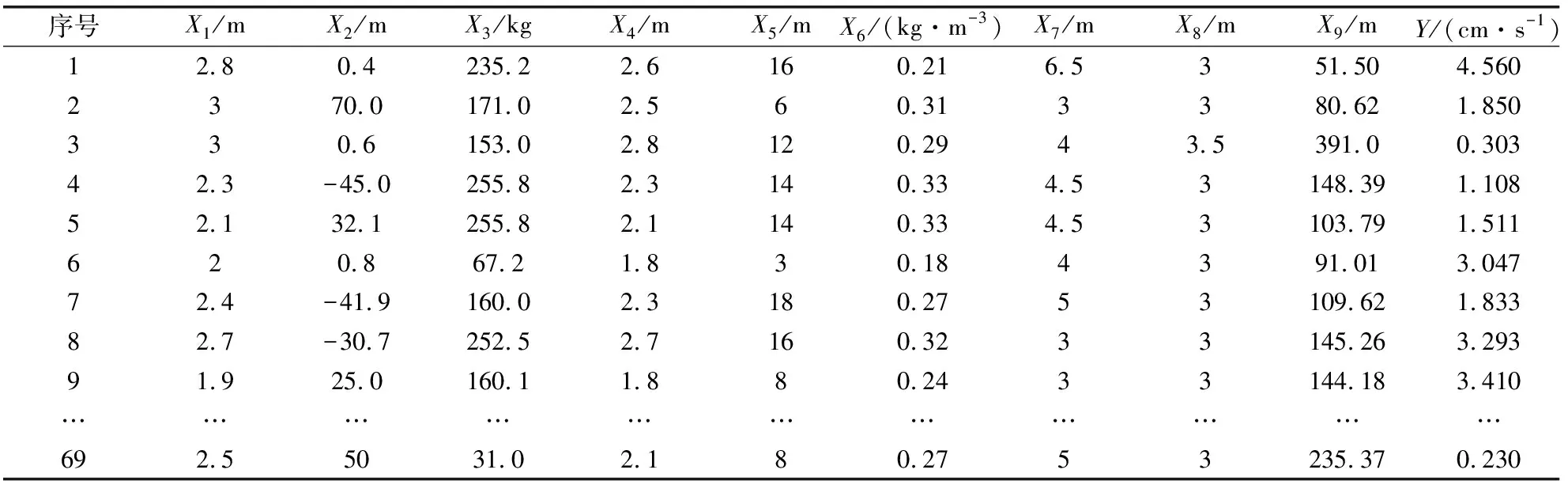
表1 原始爆破实测数据

表2 归一化后样本数据

3.2 影响因子的主成分分析过程

本文利用SPSS软件对影响爆破振动速度的9个因子进行主成分分析，通过Correlation Matrix窗口中计算得到爆破振动速度影响因子的相关系数矩阵如表3所示。求解矩阵对应的特征值λi，计算各成分贡献率及累计贡献率，结果如表4所示。

表3 相关系数矩阵

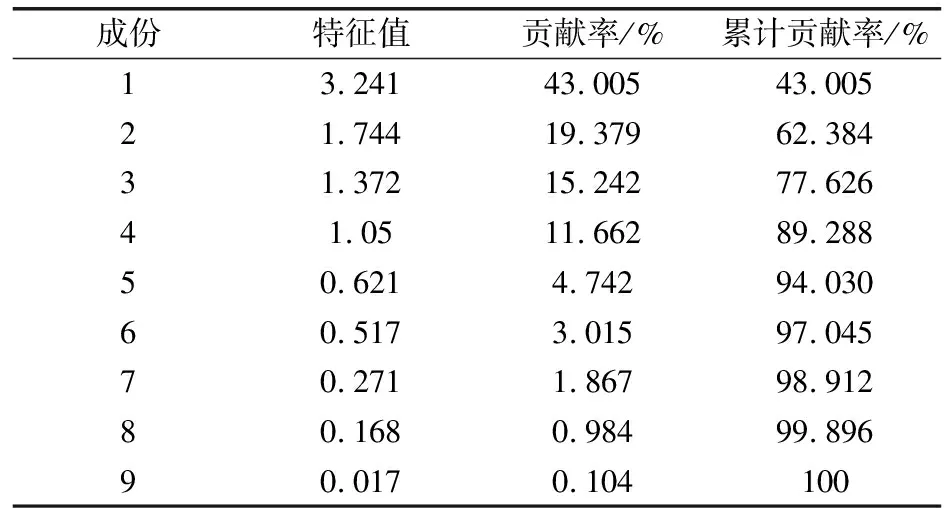
表4 特征值、贡献率及累计贡献率

由表4可知，前4个因子的累计贡献率为89.288%>85%，即这4个主成分可以代表原始数据89.288%的信息，将提取主成分后的数据输入GA-SVM模型进行学习，模型维度由原来的9维降为4维，可大大提高模型的计算和收敛速度。各主成分对应的得分系数如表5所示。

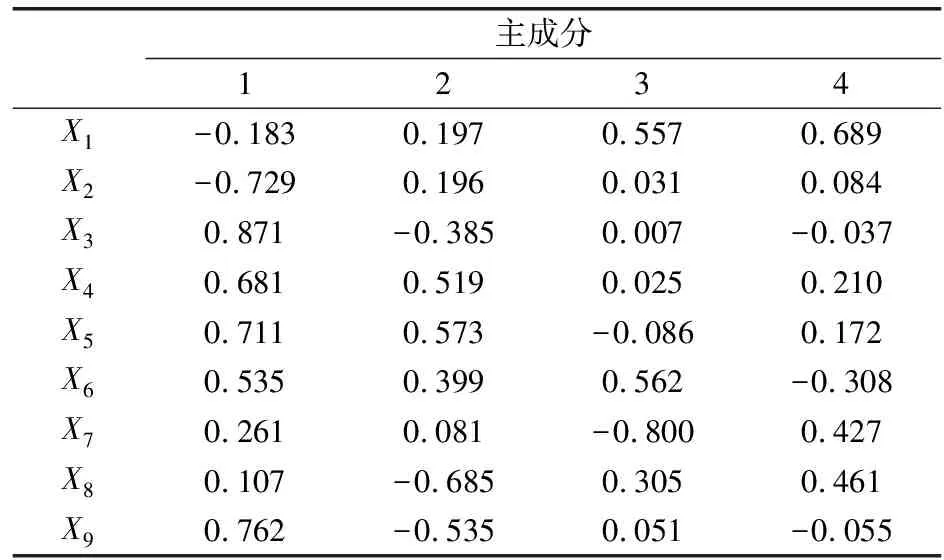
表5 主成分得分系数

由表5可得出主成分表达式，即：

F1=-0.183X1-0.729X2+0.871X3

+0.681X4+0.711X5+0.535X6+0.261X7

+0.107X8+0.762X9

F2=0.197X1+0.196X2-0.385X3

+0.519X4+0.573X5+0.399X6+0.081X7

-0.685X8-0.535X9

F3=0.557X1+0.031X2+0.007X3

+0.025X4-0.086X5+0.562X6-0.800X7

+0.305X8+0.051X9

F4=0.689X1+0.084X2-0.037X3

+0.210X4+0.172X5-0.308X6+0.427X7

+0.461X8-0.055X9

根据前4个主成分的得分系数可知，高程差X2、最大段药量X3和爆心距X9占F1的主要部分，方差贡献率达43.005%，可以认为F1反映了爆破设计参数对振动速度起主要作用；同理F2主要反映最小抵抗线X4、孔深X5和排距X8的次要影响，方差贡献率为19.379%；F3反映设计单耗X6和孔距X7的相关信息，方差贡献率为15.242%；F4反映填塞长度X1的信息，其贡献率为11.662%。根据上述主成分表达式重新计算69组原始数据样本，可得到爆破振动速度影响因素提取主成分后的数据统计(见表6)。

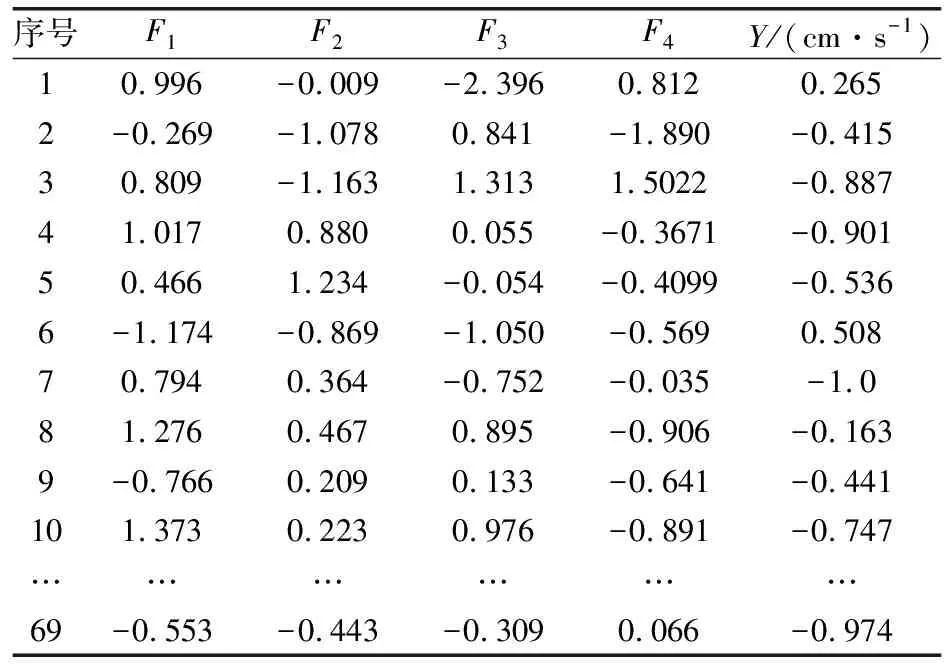
表6 提取主成分的样本数据

3.3 PCA-GA-SVM预测模型建立及分析

本文采用LIBSVM软件包进行SVM关键参数的优化。该软件包由台湾大学林智仁教授等开发，可以支持操作者在MATLAB平台上对源代码进行修改、编译，能够高效地识别和训练SVM模型。PCA-GA-SVM预测模型的各参数设置如下：核函数设置为径向基核函数，种群最大数量为20，最大迭代数为100，交叉概率为0.6，变异概率为0.1。从表6中随机选取58组数据作为学习样本训练GA-SVM模型，剩下的11组作为待测试样本进行预测。经过100次的迭代寻优，得到的适应度曲线如图2所示。

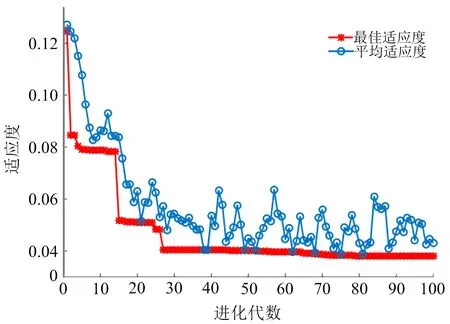
注：最优c=1.899 1、g=1.971 2，均方误差MSE为0.037 86。图2 PCA-GA-SVM模型的适应度Fig.2 Fitness of PCA-GA-SVM model

由图2可知，当种群迭代100次终止后，SVM模型有最优组合(c=1.899 1、g=1.971 2，均方误差MSE为0.037 86)，将其代入模型对训练样本仿真测试，得到样本拟合回归曲线(见图3)。可以看出，PCA-GA-SVM对于训练样本集的回归拟合效果良好，此时最小均方差MSE=0.003 751，能够用来预测分析实际爆破工程中的振动速度。

图3 PCA-GA-SVM训练样本拟合回归曲线Fig.3 PCA-GA-SVM training sample fitting regression graph

3.4 不同模型预测效果对比

为测试PCA-GA-SVM模型的准确率，通过与上述相同的训练样本和测试样本，分别与BP神经网络模型、传统SVM模型和GA-SVM模型进行预测对比。其中，GA-SVM模型中的输入变量为未经PCA分析的原始样本数据，传统SVM模型的参数利用交叉验证获得，上述4种模型的测试结果如图4所示。为评价模型预测精度，各预测模型的平均相对误差、均方差(MSE)和建模时间的具体数值如表7所示。

图4不同预测模型测试结果Fig.4 Test results of different prediction models

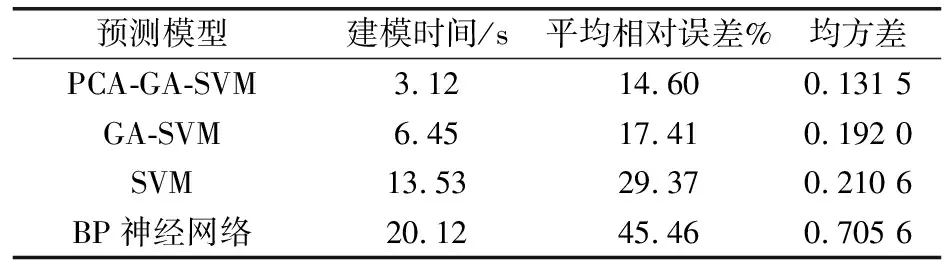
表7 各模型预测效果对比

从图4和表7可以看出，BP神经网络模型预测效果最差，其平均相对误差为45.46%，均方误差为0.705 6，这说明BP神经网络模型对小样本学习和泛化能力较差；GA-SVM模型的平均相对误差比传统SVM模型减小了11.96%，均方差为0.192 0，说明经GA算法优化后得到的关键参数大大提高了SVM模型的准确率；而PCA-GA-SVM模型比传统SVM模型和GA-SVM模型平均相对误差分别减小了14.77%和2.81%，均方误差达到0.131 5，收敛时间缩短了10.41 s和3.33 s，进一步说明了同时结合PCA和GA算法建立的PCA-GA-SVM模型具有更快的收敛速度和更高的预测精度，能够准确地预测分析爆破振动速度。