累积效应下初支混凝土爆破损伤规律研究

王海龙，李 帅, 赵 岩

(1.河北省土木工程诊断、改造与抗灾重点试验室，河北 张家口 075000 ；2.河北寒冷地区交通基础设施工程技术创新中心，河北 张家口 075000；3.中国矿业大学(北京)力学与建筑工程学院，北京 100083)

钻爆法施工中，在循环爆破作业下，初支混凝土往往要在达到终凝强度前承受循环的爆破荷载的冲击。这必然会引起初支混凝土内部产生劣化，导致其宏观力学性能降低[1-2]，减弱支护结构的支承能力，进而威胁到隧道内施工人员的人身安全。因此对初支混凝土在循环爆破作用下的损伤规律的研究很有必要。

声波测试作为一个无损的测试方法，具有操作简便性、成果易判读等优点，因此，学者们越来越多使用此方法研究爆破损伤效应。夏文俊等[3]基于不同爆破方式下爆前爆后岩体声波速度的对比检测数据以及坝基岩体钻孔内预埋速度传感器的振动测试结果，建立坝基岩体损伤程度与质点峰值振速的对应关系，提出与声波速度降低率相关的质点峰值振速安全阈值; Yong Fang等[4]利用超声波检测对竖井周围的爆破损伤区(BDZ)进行了测试，并将其纳入收敛约束法(CCM)和三维数值分析中，以评估BDZ对围岩衬砌的影响；单仁亮等[5]研究发现，距掌子面的距离与喷射混凝土累积损伤之间存在退化的非线性关系。

现有研究成果主要集中在围岩的爆破损伤效应[6-10]，而对初支混凝土的爆破累积损伤研究相对较少[11-12]。为研究初支混凝土的爆破累积损伤，本文引入等效距离和等效药量的概念，通过优化爆破损伤公式研究初支混凝土考虑累积效应的爆破损伤规律。

1 工程监测

1.1 工程背景

本文以某铁路隧道正洞爆破工程为背景，正洞洞身主要穿越早远古代变质岩系红旗营子群斜长片麻岩等，弱风化，节理裂隙发育，岩体较完整围岩稳定性一般～较差，初期支护采用C25喷射混凝土。本文使用的爆破振动信号和喷射混凝土的声波数据均由此隧道正洞小里程钻爆法施工产生。

1.2 监测方案

爆破振动信号的采集使用M20型爆破测振仪，同时采集x、y、z方向上的爆破振动速度，并对所测数据进行初步分析并提取质点峰值振速(PPV)，数据采集过程中使用不锈钢夹片将传感器固定于隧道内线路行进方向右侧约1.5 m高度处，传感器y方向指向隧道掘进方向，x方向指向隧道径向，z方向垂直于xy平面上。声波波速的采集使用RSM-SY5(T)非金属声波检测仪采集现场爆破施工前后爆破振速监测点旁所设观测点的声波数据，测点布置如图1所示。

图1 测点布置Fig.1 Layout of measuring points

2 振速衰减规律

考虑到分段爆破同一段位的多个炮孔与振动传感器的距离不相同，各段位炮孔装填炸药量也不同，为此使用等效药量和等效距离代替最大段位药量和爆心距[13]：

(1)

(2)

式中：R′为等效距离；Q′为等效药量；qi为同段第i个炮孔装药量；ri为同段第i个炮孔距离传感器的距离。

各测点PPV及对应的爆破参数如表1所示，通过式(1)和式(2)即可得到基于萨道夫斯基公式的振速衰减公式：

(3)

分别由萨道夫斯基公式和式(3)对表1数据进行拟合，可得到PPV值的预测公式：

(4)

(5)

式(4)和式(5)预测的PPV值与实测数据对比如表2所示，除个别测点外，式(5)预测值的相对误差皆小于式(4)。

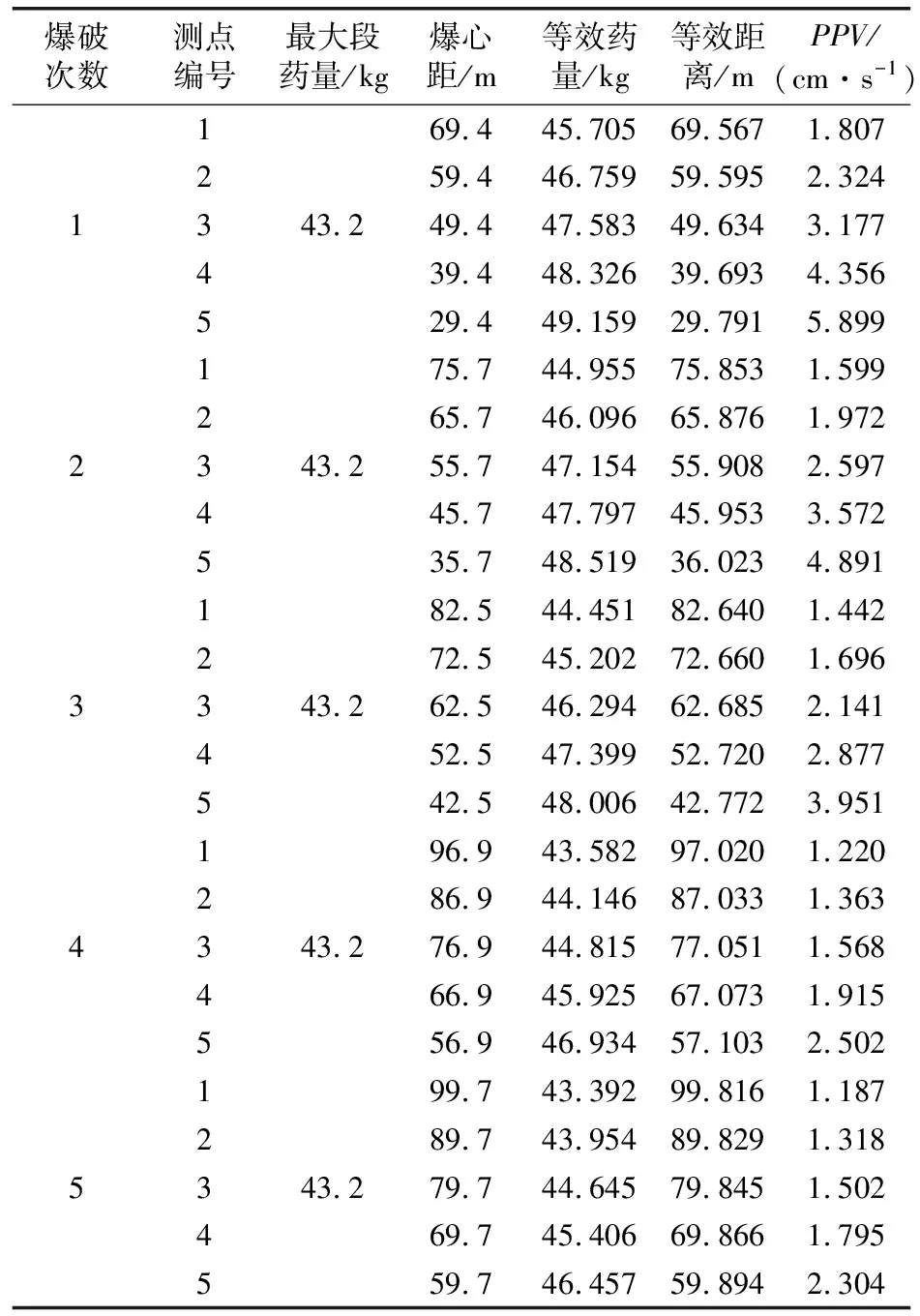
表1 各测点PPV及对应的爆破参数

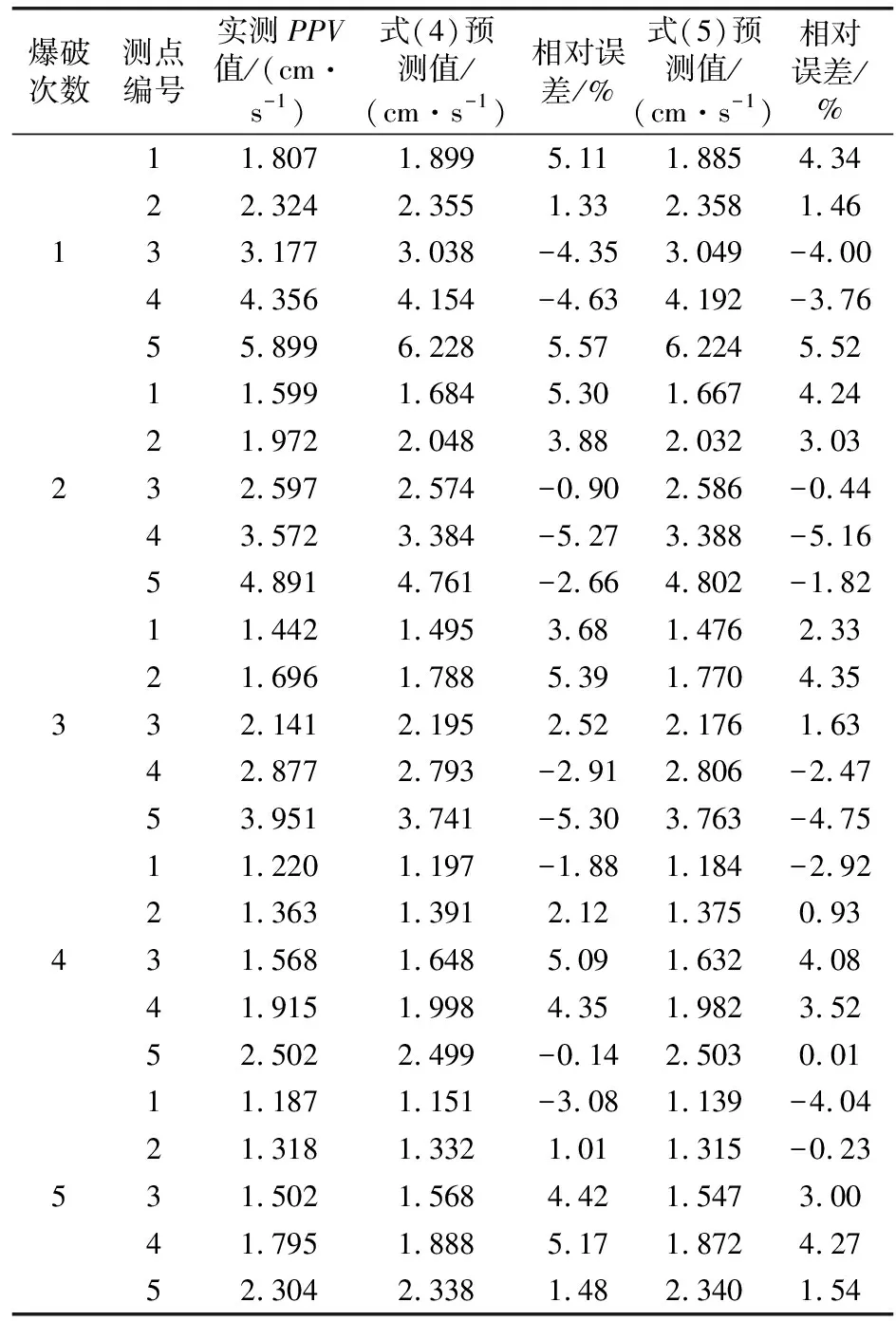
表2 预测数据与实测数据对比

3 爆破损伤规律

初支混凝土在循环爆破作用下宏观力学性质的劣化，可表现在声波速度的降低[14-16]，现场采集的声波数据如表3所示。

表3 各测点声波监测数据

在计算围岩累积损伤时，工程上常使用同部位爆破前后围岩声波速度变化率η来衡量损伤度D，即

(6)

式中：v0和v分别为爆破前、后的围岩声波速度。

隧道初期支护混凝土在循环爆破荷载作用下，其力学性能的不断劣化，可用公式表示为

(7)

式中：E0为爆破前围岩的弹性模量。

根据弹性力学相关知识，爆破前岩体声波纵波波速为

(8)

式中：E为围岩的弹性模量；ρ为围岩密度；μ为泊松比。

联立式(6)～式(8)，可得

(9)

则损伤增量可表示为

(10)

式中：ΔDi为第i次(i=1,…,n)爆破后初支混凝土损伤增量；vi为第i次爆破作用后初支混凝土的声波速度。

故第n次爆破作用后，初支混凝土的累积损伤度可表示为

(11)

式中：D0为初支混凝土的初始损伤，本文中假设初始损伤D0取值为0。

爆破前后损伤增量ΔD和累积损伤D如表4所示，除1号测点外，经过5次爆破后累积损伤D均大于或等于0.19，达到临界破坏值[17]，可以认为爆破作用对初支混凝土产生了损伤。

表4 爆破前后损伤增量和累计损伤

分析表3和表4数据即可得到初支混凝土累积损伤规律(见图2)，随着爆破次数增加，累积损伤也在变大，但损伤增量却在逐渐减少，与损伤增量图像相应的是爆破累积损伤呈斜率逐渐减小的非线性增长，主要原因在于距离爆破中心距离越来越远，爆破作用影响逐步减弱。损伤增量与等效距离的关系与PPV随等效距离增加的衰减规律具有相似性(见图3)。经Shapior-wilk检验，PPV和损伤增量均符合正态分布，且Pearson相关性系数均大于0.97，显著性检验结果显示PPV和损伤增量具有较为显著的线性相关性(见表5)。通过使用损伤增量数据对PPV衰减公式进行拟合，拟合后的r2均大于0.9，拟合结果如下

(12)

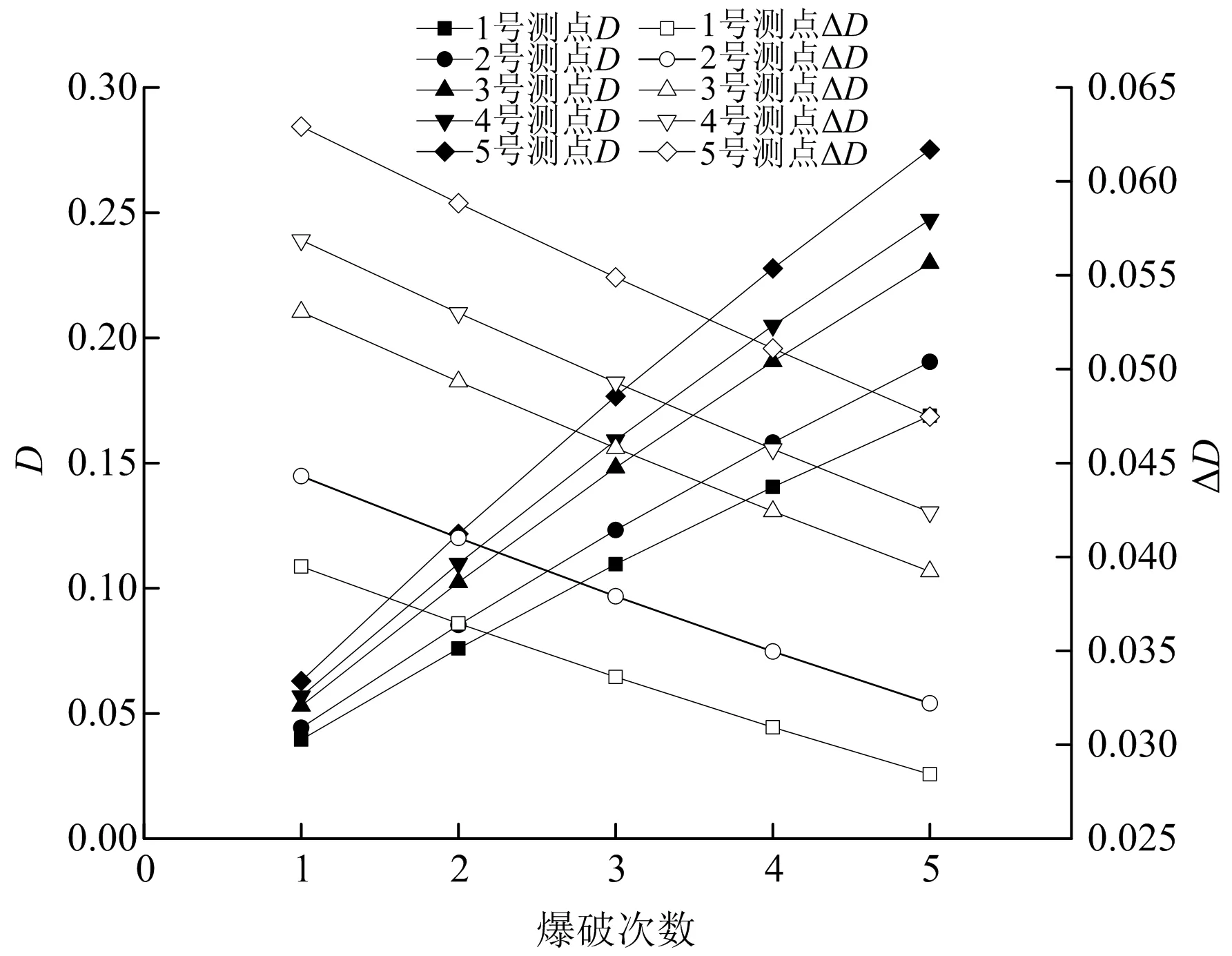
图2 爆破损伤与损伤增量的变化规律Fig.2 Variation law of blasting damage and damage increment

图3 损伤增量和PPV随等效距离变化的关系Fig.3 The relationship between damage increment and PPV with equivalent distance

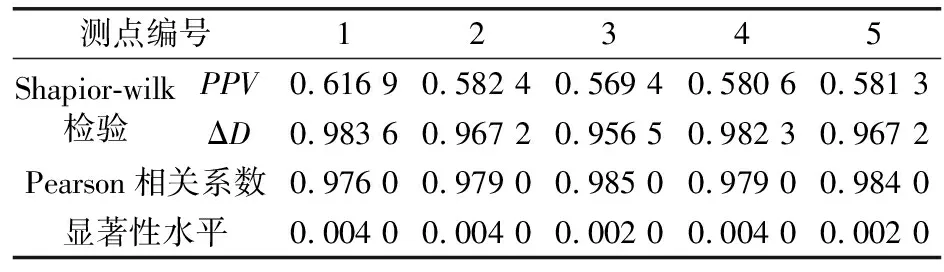
表5 损伤增量和PPV相关性检验

4 结论

1)用等效药量和等效距离代替最大段位药量和爆心距得到的PPV衰减公式与传统的萨道夫斯基经验公式相比，PPV值的预测结果更加接近实测值。

2)根据弹性力学相关知识推导了爆破损伤增量的公式， 5个测点爆破损伤增量的计算结果表明，距爆源较近的4个测点在5次爆破后均达到了爆破损伤限值0.19，可以认为爆破作用对初支混凝土产生了不利影响。

3)爆破累积损伤随爆破次数呈非线性增加的规律，但损伤增量随爆破次数增加呈现逐渐减小的趋势，损伤增量随等效距离变化的关系与PPV衰减规律相似且损伤增量和PPV具有较为显著的线性相关性。