水下爆炸气泡运动对水面形态影响的数值模拟

2021-09-06刘筹资查恩尧欧阳和平程永舟郭锦泽郑长青

工程爆破 2021年4期

刘筹资，查恩尧，欧阳和平，程永舟，郭锦泽，郑长青

(1.长沙理工大学水利工程学院，长沙 410114；2.中交第四航务工程勘察设计院有限公司，广州 510000；3.湖南水利水电职业技术学院，长沙 410100；4.珠海爆破新技术开发公司，广东珠海 519099)

水下爆炸技术作为一种快速有效的水下施工手段，在航道疏浚[1]、水下岩石开挖[2]、水下结构拆除[3-4]等工程中应用广泛。水下爆炸在不同条件下会形成多阶段的物理现象，当水下爆炸发生在水面附近时，除冲击波传播、气泡脉动现象外，气泡在脉动过程中还会与水面相互作用在水面附近形成形态不同的水冢[5]。在重力作用下，水冢冲击水面形成的波浪，会对周围结构特别是舰船等浮体结构产生较大影响。因此开展水下爆炸气泡运动对水面形态变化影响的研究，对深入了解近水面水下爆炸现象，指导水下爆炸实施时对周边结构物的防护具有重要意义。

在爆炸兴波方面，沈国光等[6-7]基于MAC算法将爆炸气泡与自由液面的相互作用过程简化，这一方法虽然能够简化水下爆炸的过程，但赋予气泡的内压是以与试验水面现象的异同作为标准的，因此只能作为特定装药量的计算，此外由于模拟中忽略了气泡脉动、射流的过程，对于兴波机理的讨论是不充分的。Safiyari等[8-9]基于SPH方法，将兴波过程简化为空腔的扩张、坍缩，进而引起水面波动的过程，这一研究同样忽略了气泡脉动、射流现象在水面形态形成中的关键作用。王志凯[10]基于ALE算法研究了水下爆炸气泡破碎兴波对浮动冲击平台的影响，该研究中虽然考虑了气泡脉动，但其计算工况中，水深距离参数达到了2.7，依据文献[11-13]，该条件下气泡与自由液面相互作用形成的水冢对自由液面的扰动很小，能够形成的兴波波浪也较小，并且由于模型设置了浮体结构，水冢的发展以及兴波波浪的形成也会被抑制。刘云龙等[12]基于BEM方法也讨论了气泡破碎兴波对浮体结构的影响，但仅限于气泡脉动成简化的锥形水冢冲击水面形成的波浪与浮体结构的相互作用。李汪讳等[14]、Wang等[15]基于BEM方法对水下爆炸兴波现象进行了模拟，但文献[14]未讨论各种水冢形态对水面兴波的影响，文献[15]简化了水冢形态，忽略不连续水体，将气泡运动在水面附近形成的水冢分别简化为水下空腔和水面水柱两种形态。前人在兴波方面的研究由于采用的BEM方法对不连续边界的模拟存在困难，基本都建立在一定的水冢形态简化条件下进行，这与实际的水面现象不相符，对于水面波动发展过程的讨论也存在一定的误差。

基于此，本数值模拟研究采用LS-DYNA非线性有限元软件，基于ALE算法，结合水冢形成过程及其特征几何参数、气泡运动特性与水面波动过程，就不同水深距离参数下水下爆炸气泡运动对水面形态的影响机理开展研究。

1 气泡运动数值模型的建立

1.1 算法选择与几何模型的建立

由于炸药爆炸的气体产物在水下形成的气泡存在着膨胀收缩过程，在气泡运动的影响下水面会存在复杂的变形，同时为了捕捉气泡的运动特性，对于气泡边界的捕捉也具有一定的要求。因此，本研究采用ALE算法进行三维数值模拟。模型中涉及到的炸药、水和空气均采用ALE算法。

为了兼顾计算效率，采用三维1/4模型，在对称面上施加对称边界条件，在空气域和水域外边界处设置pressure outflow边界单元层，以模拟无限边界条件，模型的x、y方向和装药下方的水域深度应至少为气泡脉动最大半径的4倍，空气层的高度则需满足水冢中心水柱向上发展的要求。为了提高计算效率同时保证模拟结果的正确性，在气泡最大半径1.5倍范围内采用与装药半径尺寸相同的均匀网格，其他区域采用由均匀网格区域至流域外边界逐渐渐变的网格，渐变网格最小处与均匀网格相同，最大处网格尺寸为均匀网格的10倍。几何模型如图1所示。

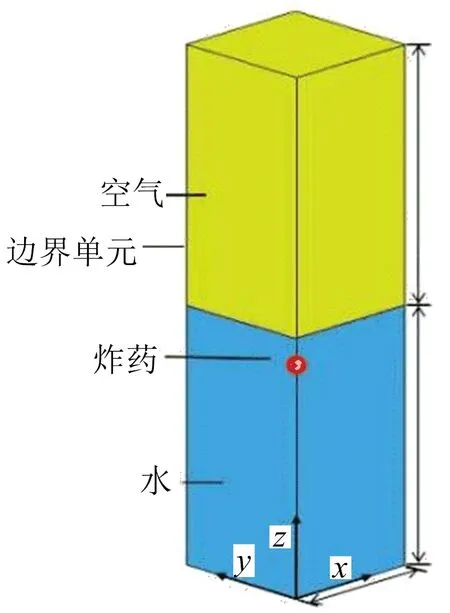
图1 几何模型Fig.1 Geometric model

1.2 材料模型的设置

模型主要涉及炸药、水和空气3种物质，其中炸药采用JWL状态方程进行描述，水采用Grüneisen状态方程进行描述，空气采用线性多项式状态方程进行描述。各材料的具体参数如表1～表3所示[16-17]。

表1 TNT炸药的材料方程和状态方程参数取值

表2 水的材料方程和状态方程参数取值

表3 空气的材料方程和状态方程参数取值

1.3 气泡运动模型有效性验证

为了验证气泡运动模型的有效性，设置与文献[18]实验相同的工况，使用5.2 g TNT的球形装药(与实验中4 g PENT炸药等效)，装药半径为0.009 132 m，模型计算尺寸为1 m×1 m×4 m，渐变网格划分尺寸最小为0.009 m，最大为0.1 m，均匀网格处网格尺寸为0.009 m。

由自由场条件下文献[18]中实验结果和数值模拟结果的对比(见图2)可以发现，在自由场条件下数值模拟的气泡运动趋势与文献中的各个阶段保持一致；由在近自由液面条件下文献[18]中实验结果和数值模拟结果进行的对比(见图3)可知，两者气泡运动趋势大致一致。

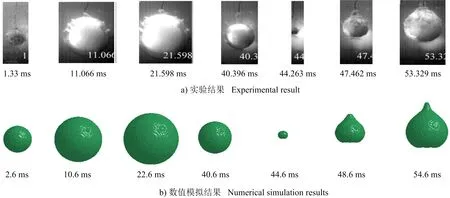
图2 自由场条件下气泡运动趋势对比Fig.2 Comparison of bubble movement trends under free field conditions

图3 近自由液面条件下气泡运动趋势对比Fig.3 Comparison of bubble movement trends under the condition of near free liquid surface

对于水下爆炸气泡脉动的第一周期及气泡半径计算，已经形成了能够应用于工程实际的经验公式[19]：

(1)

(2)

式中：R为气泡第一次脉动的气泡最大半径，m；T为脉动周期，s；W为装药当量，kg；D为装药位置处水深，m；10.3为大气压强对应液柱高度，m；K4、K5为与炸药相关的计算参数。

常见气泡脉动参数取值如表4所示[19]。

表4 气泡脉动经验公式计算参数

另外也对自由场和近水面条件下的气泡半径时程进行了分析，数值模拟结果数据与文献[18]中的工况数据进行对比分析发现两者之间的误差在10%以内(见表5)，为了体现研究的严谨性又对经验公式[19]的结果进行了计算对比，分析发现在两种条件下气泡的半径和周期变化误差均在10%以内(见表5)，说明气泡运动数值模型与实验结果一致性良好。

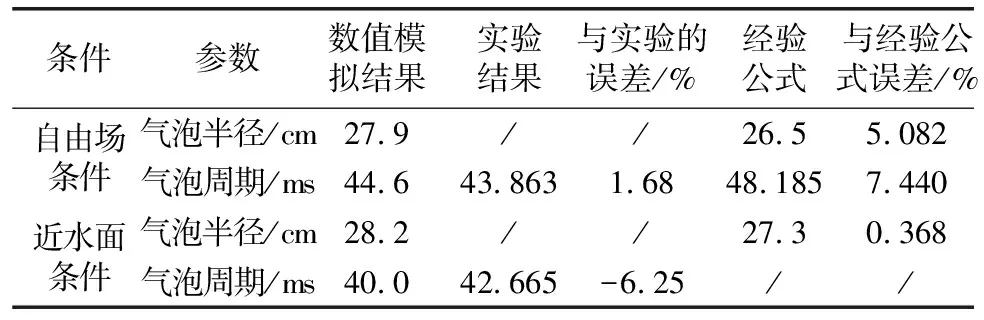
表5 气泡半径与周期误差计算结果

1.4 网格尺寸对计算精度的影响

为了讨论网格尺寸大小对计算精度的影响，以5 kg TNT装药，在水面下1 m处爆炸为例，在理论气泡脉动第一周期最大半径的1.5倍范围内分别划分0.9、1.0、1.1、1.2倍装药半径(0.09 m)的均匀网格，其余水域网格划分由内至外逐渐增大，最大处为内部均匀网格尺寸的10倍。模型大小为20 m×20 m×30 m，水域高15 m，空气域高15 m。

将计算所得的气泡体积等效为规则圆的半径并与经验式(1)结果进行对比，得到了不同网格条件下的气泡第一周期脉动最大半径(见表6)，可以看出在几种工况下，不同的网格尺寸的相对误差均不超过5%。其中，当网格尺寸与装药半径为0.9倍和1.0倍时，气泡第一周期脉动最大半径分别为2.629 m和2.633 m，两者与经验公式的理论半径都较为接近，但采用0.9倍装药半径与网格尺寸的计算时长相较于1.0倍装药半径与网格尺寸约增加一半。在综合考虑计算精度和计算效率的条件下，本文计算模型中心区域的均匀网格尺寸选取为1.0倍装药半径大小。

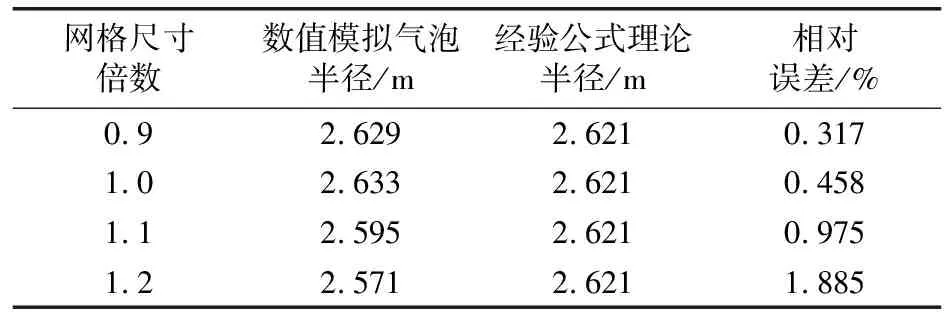
表6 不同网格条件下气泡参数计算结果

2 气泡运动对水面形态的影响

2.1 模型设置

由于验证模型采用的是5.2 g的球形TNT炸药，不便对气泡运动对水面形态变化的影响进行研究，因此建立尺寸为10 m×10 m×30 m的模型，水域、空气域各高15 m，采用5 kg球形TNT装药。

2.2 装药深度对气泡运动特性的影响

水下爆炸气泡在不同装药水深条件下将会出现不同的运动特性，为了研究装药深度对其运动特性的影响，首先定义装药水深H为水下装药位置距水面的距离，炸药起爆位置在水面以下1～5 m的模型中心处，设置9种不同工况，各个工况之间间隔0.5 m。

由不同装药深度条件下气泡垂直方向位移的变化情况(见图4)可以看出，在H为1.0～3.0 m时，气泡垂直方向位移呈现先上后下的变化趋势，且移动大小随装药水深的增大而减小，当H>3.0 m时，气泡垂直方向位移逐渐向上移动。

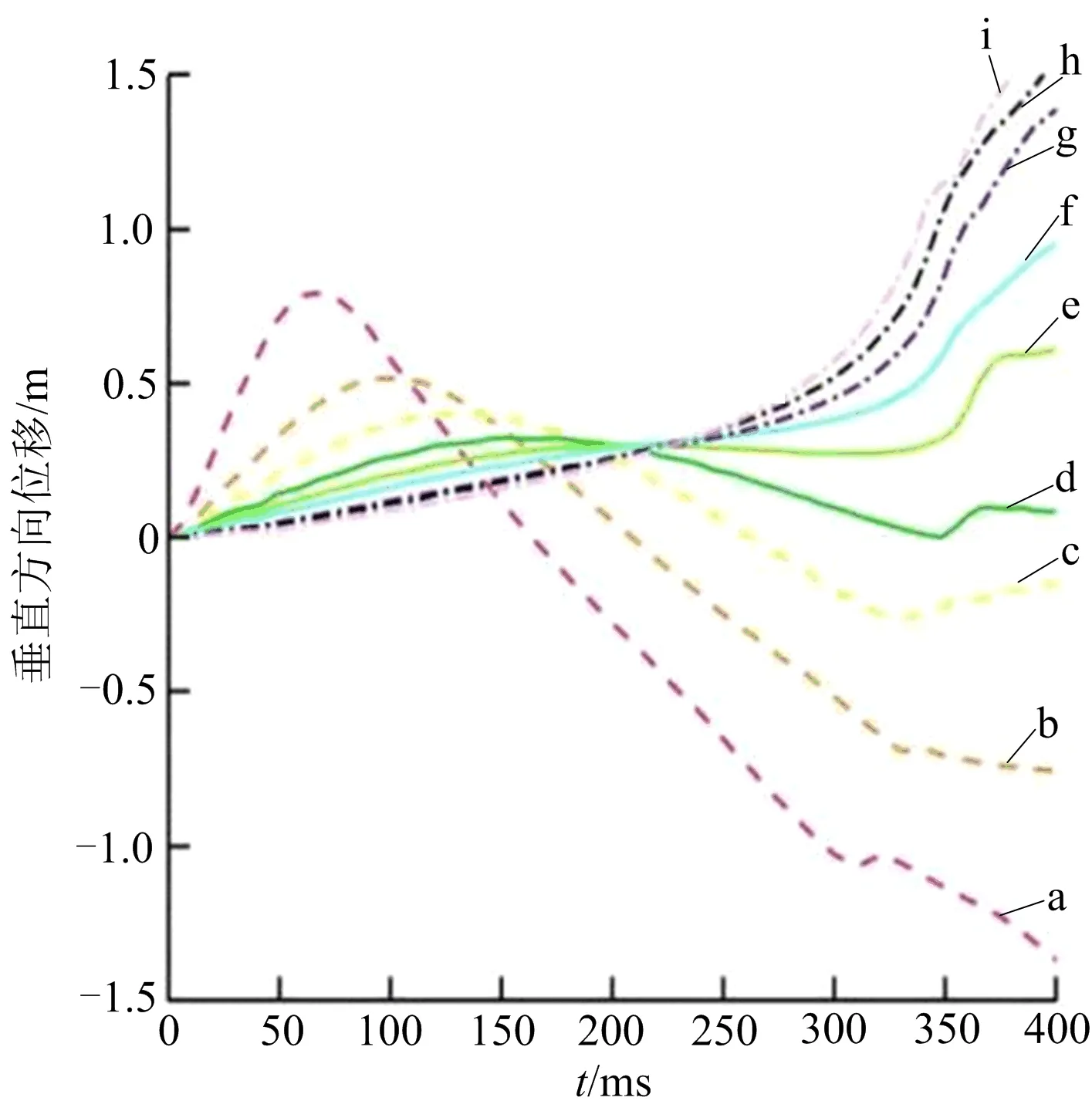
注：a～i分别代表H为1.0、1.5、2.0、2.5、3.0、3.5、4.0、4.5、5.0 m。图4 水深对气泡垂直方向位移的影响Fig.4 Influence of water depth on the vertical displacement of bubble

由不同装药深度下气泡半径的变化情况(见图5)可以发现，气泡脉动第一周期时长随着装药深度的增大逐渐延长，从以上分析可知在2.0～3.0 m装药水深范围内存在一个临界水深。当装药水深小于临界水深时，气泡脉动第一周期最大半径与脉动第一周期时长随装药水深的增大而增大，气泡中心点的位移先向上后向下，且移动大小随装药水深增大而减小；当装药水深大于临界水深时，气泡脉动第一周期最大半径与脉动第一周期时长随水深的增大而减小，气泡中心点向上位移大小随水深增大而增大。

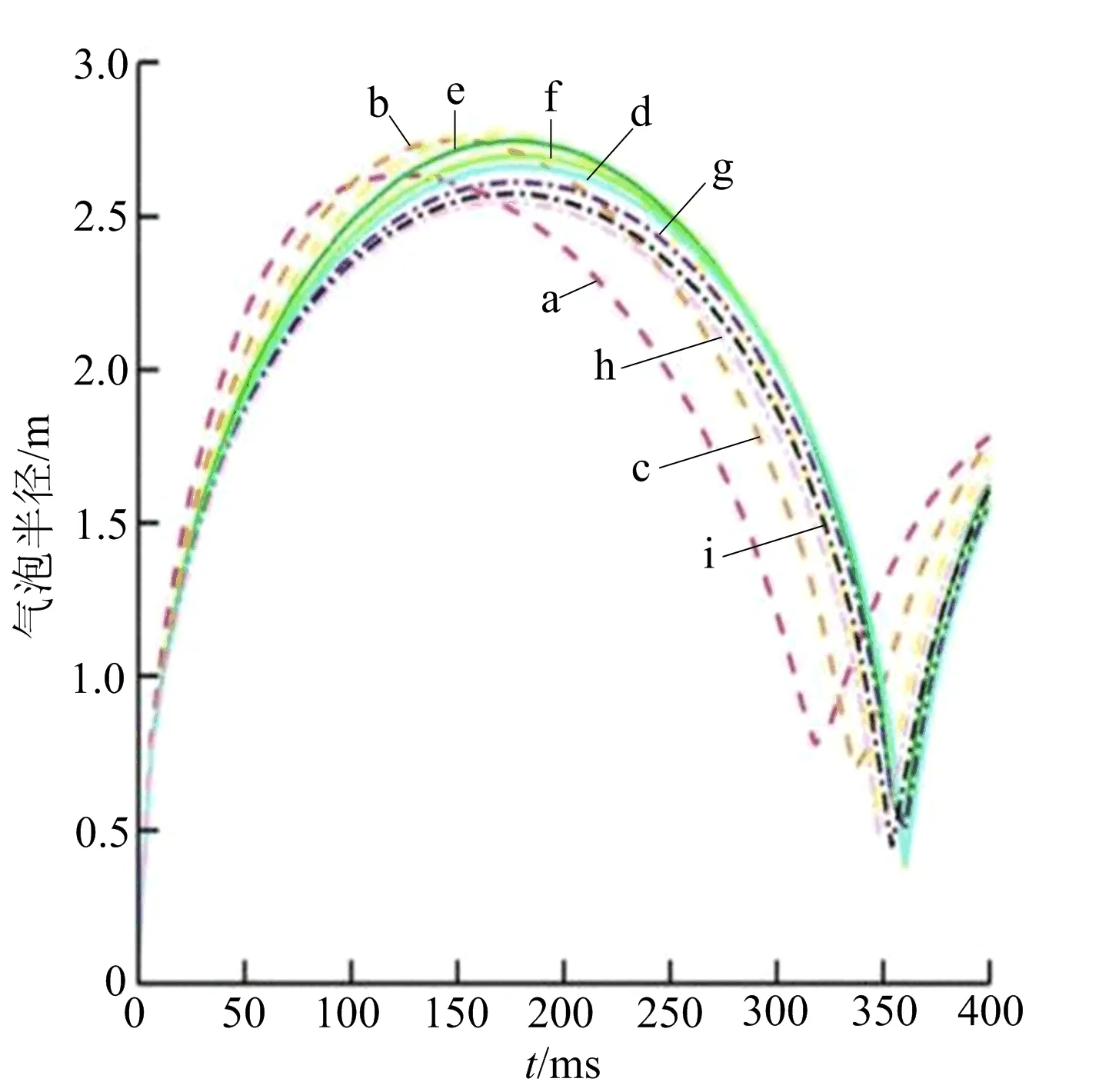
注：a～i分别代表H为1.0、1.5、2.0、2.5、3.0、3.5、4.0、4.5、5.0 m。图5 不同装药深度气泡半径变化关系Fig.5 Change relationship of bubble radius with different charge depth

2.3 水冢形成过程

气泡运动的变化也会导致水面水冢形态发生变化，因此对水冢的形成过程进行研究非常有必要。为了研究水冢的形成过程，对近水面条件下5 kg球形TNT炸药在改变不同水深距离参数时产生的不同类型的水冢形成过程进行研究。同时为了与水面中心水柱相区分，定义在水面附近形成的水体形态称之为水冢。经前人研究发现，水冢现象的形成与水深距离参数γf=H/Rmax有关[5]，H为炸药装药位置距水面的距离，m；Rmax为气泡脉动过程的最大半径，m。依据水下爆炸气泡最大半径公式，在水深距离参数γf范围在0.000 1～1.1内，讨论不同水深距离参数γf下水冢形态的特征及形成机理(空腔半径为气泡脉动第一周期所形成的实际最大半径)。

当起爆位置距水面相近时，会产生零碎型水冢(见图6)，此时水深距离参数γf为0.000 195，装药水深0.000 4 m，气泡膨胀形成的水下空腔半径为2.053 5 m。炸药起爆后，形成的气泡突出水面与空气相连通而破碎(见图6a、图6b)；在t=354 ms气泡膨胀至最大半径，形成了水下空腔，水面水体形成了零碎型水冢；在重力作用下空腔四周水体向内汇聚并形成汇聚水柱(见图6d、图6e)；t=2 094 ms时刻汇聚水柱高度到达最大值；随后受重力作用冲击水面形成波浪传播。

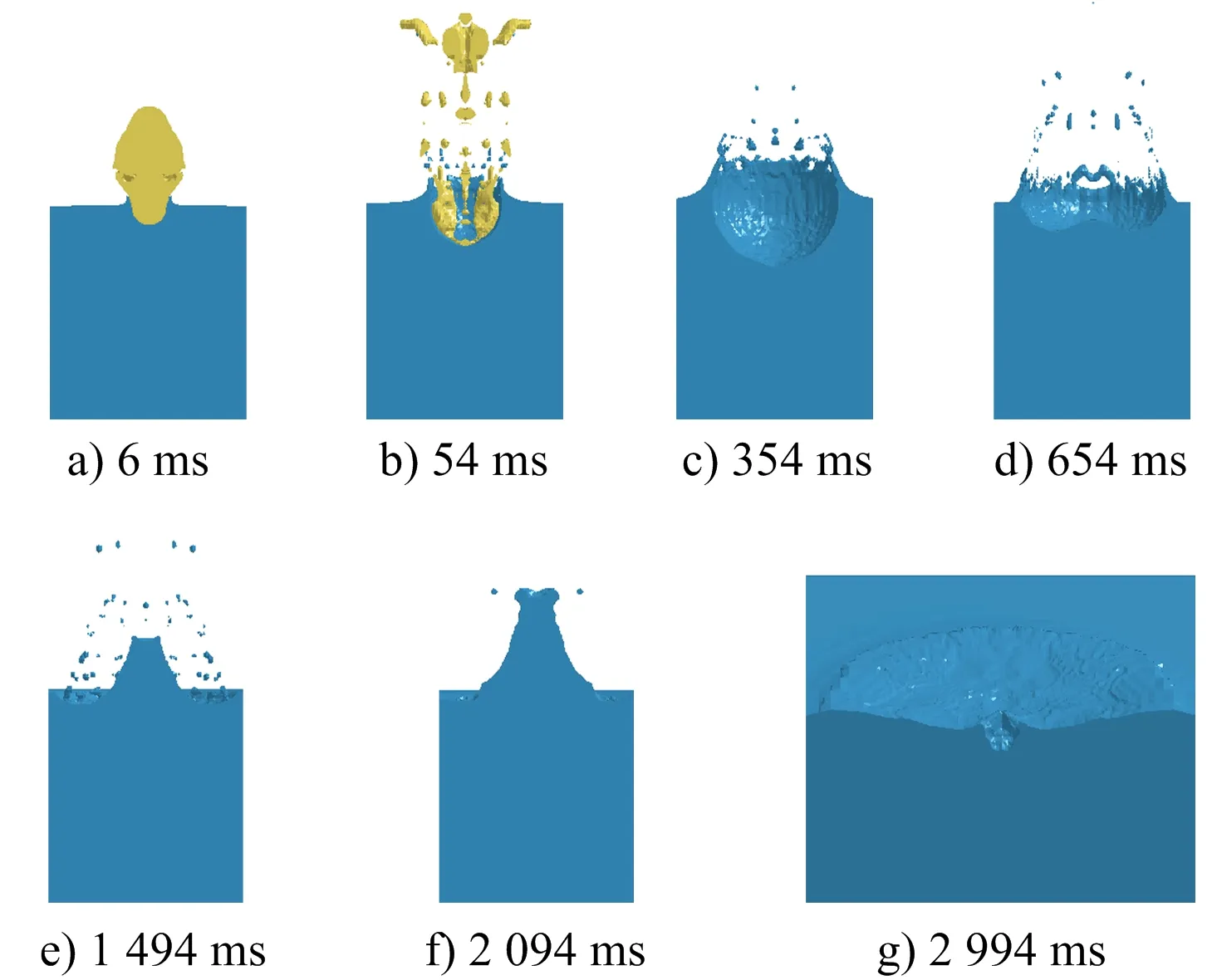
图6 零碎型水冢发展过程Fig.6 Development process of fragmented water mound

当水深距离参数γf增大到0.082 9，此时装药水深下降到0.215 m，气泡膨胀形成的水下空腔半径为2.589 m时会形成飞溅型水冢(见图7)。炸药起爆后，在t=6、54 ms时刻气泡突出水面发生破碎，并在t=174 ms时刻达到最大半径，形成空腔；t=294、594 ms时刻，由于气泡的带动，使得水体在空腔上部聚集，产生背向射流，形成飞溅型水冢。接着便在t=774、1 194 ms时刻产生类矩形的水面水柱，并在t=1 614 ms时刻达到最大值。

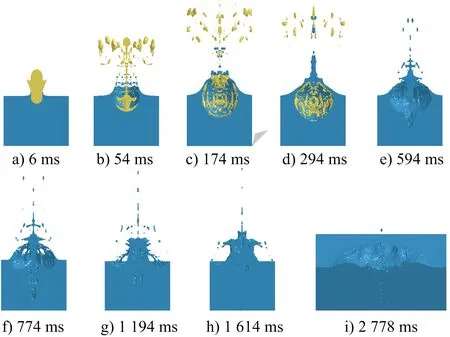
图7 飞溅型水冢发展过程Fig.7 Development process of splashing water mound

接着当水深距离参数γf增加到0.549时，装药水深为1.5 m，气泡脉动第一周期实际最大半径为2.732 m会形成酒杯型水冢(见图8)。在t=6 ms时刻，气泡开始膨胀，并在t=118 ms时刻达到最大半径；t=258 ms时刻，气泡在收缩过程中，由于受到自由液面Bjerknes力的排斥作用，会形成向下的气泡射流，进而带动水流形成向上的射流，并逐渐发展为水面中心水柱；t=318 ms时刻，气泡在向下射流的带动下，分裂为两部分，并在t=338 ms时刻达到第一周期的最小半径；t=478 ms时刻气泡再次膨胀，并且中部和上部气泡相融合，同时在气泡的推动和中心水柱的阻碍下，向上运动的水体在中心水柱周围形成了环状水体，环状水体与中心水柱一起构成了酒杯型水冢。

图8 酒杯型水冢发展过程Fig.8 Development process of wine glass water mound

最后当水深距离参数γf增大到0.998时，装药水深为2.692 m，此时气泡脉动第一周期实际最大半径为2.697 m，形成的水冢形态为皇冠型水冢(见图9)。在t=6 ms时刻，气泡开始膨胀，并在t=118 ms时刻达到最大半径；t=258 ms时刻，气泡在收缩过程中，由于受到自由液面Bjerknes力的排斥作用，会形成向下的气泡射流，进而带动水流形成向上的射流，并逐渐发展为水面中心水柱；t=318 ms时刻气泡收缩至最小半径，并在t=338 ms时刻开始二次脉动，同时向上的水射流也在不断发展，并促进了中心水柱的发展，环状水体也在气泡膨胀的推动下开始突出水面向上发展，并与中心水柱一起构成了皇冠型水冢。

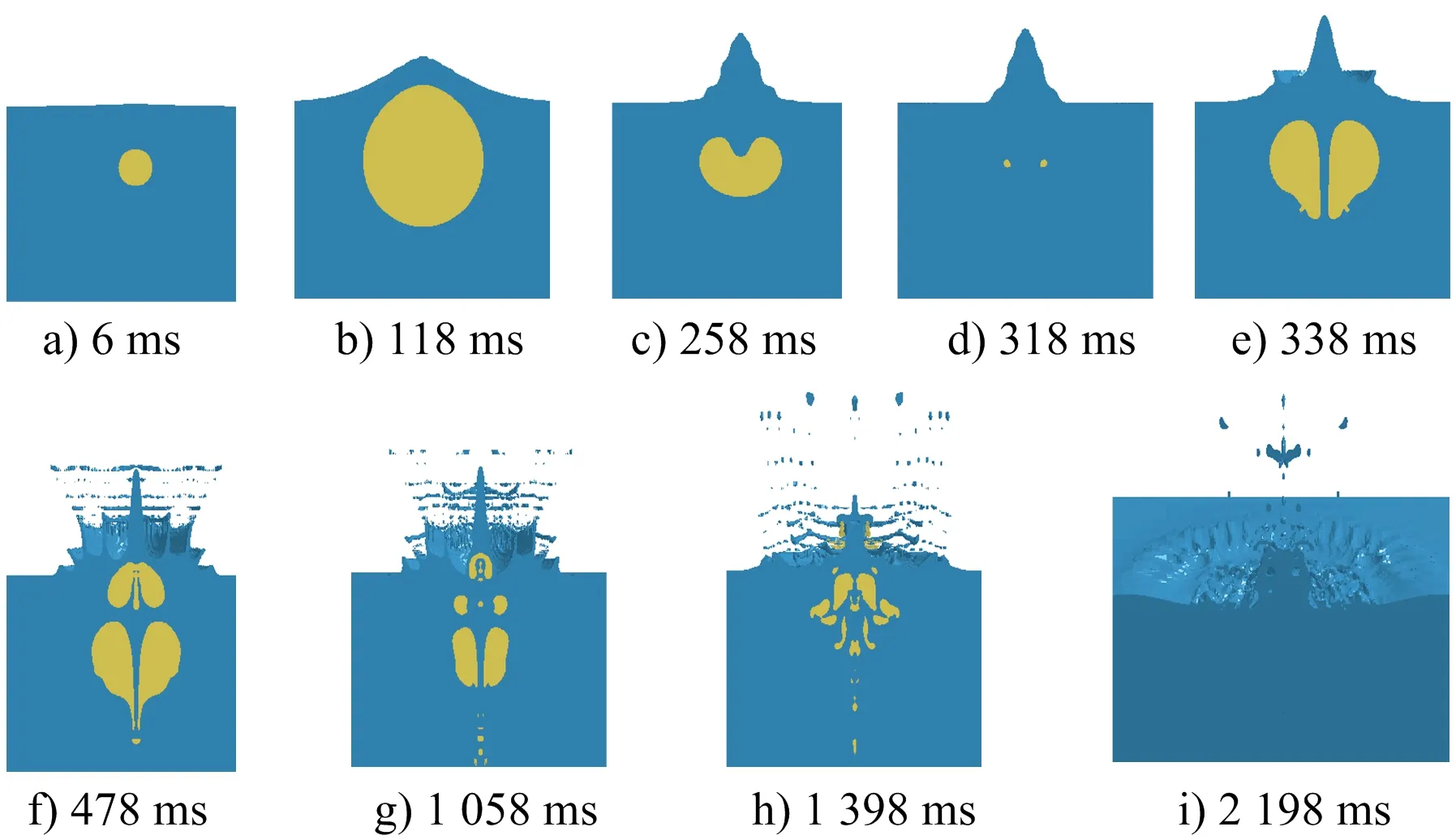
图9 皇冠型水冢发展过程Fig.9 Development process of crown-shaped water mound

2.4 水冢气泡运动特性

对上述4种不同类型的水冢气泡运动特性进行分析，由于零碎型水冢和飞溅型水冢工况下的水下爆炸气泡，炸药装药水深较浅，不能形成稳定的气泡脉动周期和射流，因此不对其运动特性进行讨论。

对于酒杯型水冢和皇冠型水冢工况下的气泡，装药水深能够满足气泡脉动所需的条件，可以形成稳定的气泡脉动与射流。通过两者气泡脉动半径、周期的对比(见图10a)可以看出，酒杯型水冢气泡脉动第一周期的最大半径为2.732 m，周期为336 ms；皇冠型水冢气泡脉动第一周期的最大半径为2.697 m，周期为360 ms。这表明气泡最大半径随着水深的增大而减小，气泡脉动周期则相反，这一现象与文献[20]得到的结论相同。

从气泡中心点在垂直方向的位移变化(见图10b)可以看出，在膨胀阶段，酒杯型水冢的气泡中心点在垂直方向上的位移明显高于皇冠型水冢，这是由于酒杯型水冢气泡所处位置水深较浅，气泡受到的外部静水压强也较小，因此膨胀阶段的阻力也是偏小的。在收缩阶段，由于受到Bjerknes力的作用形成向下射流，因此在射流和气泡收缩趋势的带动下，气泡中心位置不断下移。

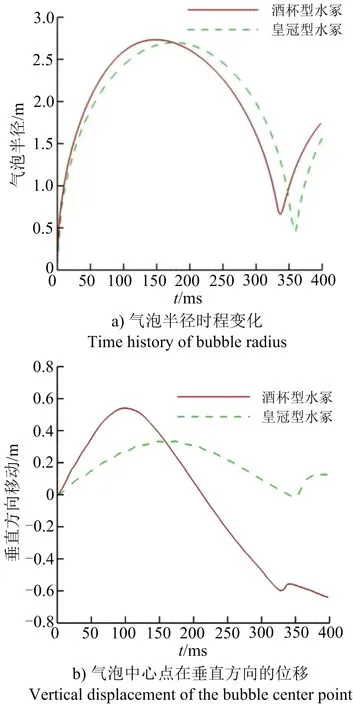
图10 酒杯型水冢、皇冠型水冢气泡运动特征对比Fig.10 Comparison of bubble movement characteristics between wine glass and crown-shaped water mound

2.5 不同类型水冢的特征参数对比

对比上述4种不同水冢的特征尺寸(见图11)可知，几种类型的水冢宽度基本处于4～5 m，与气泡最大直径相近，呈现出一定的相似性，结合上文对水冢发展过程进行详细的研究，可以知道水冢的形成过程与气泡的运动息息相关，气泡的运动特性决定了水冢形态。

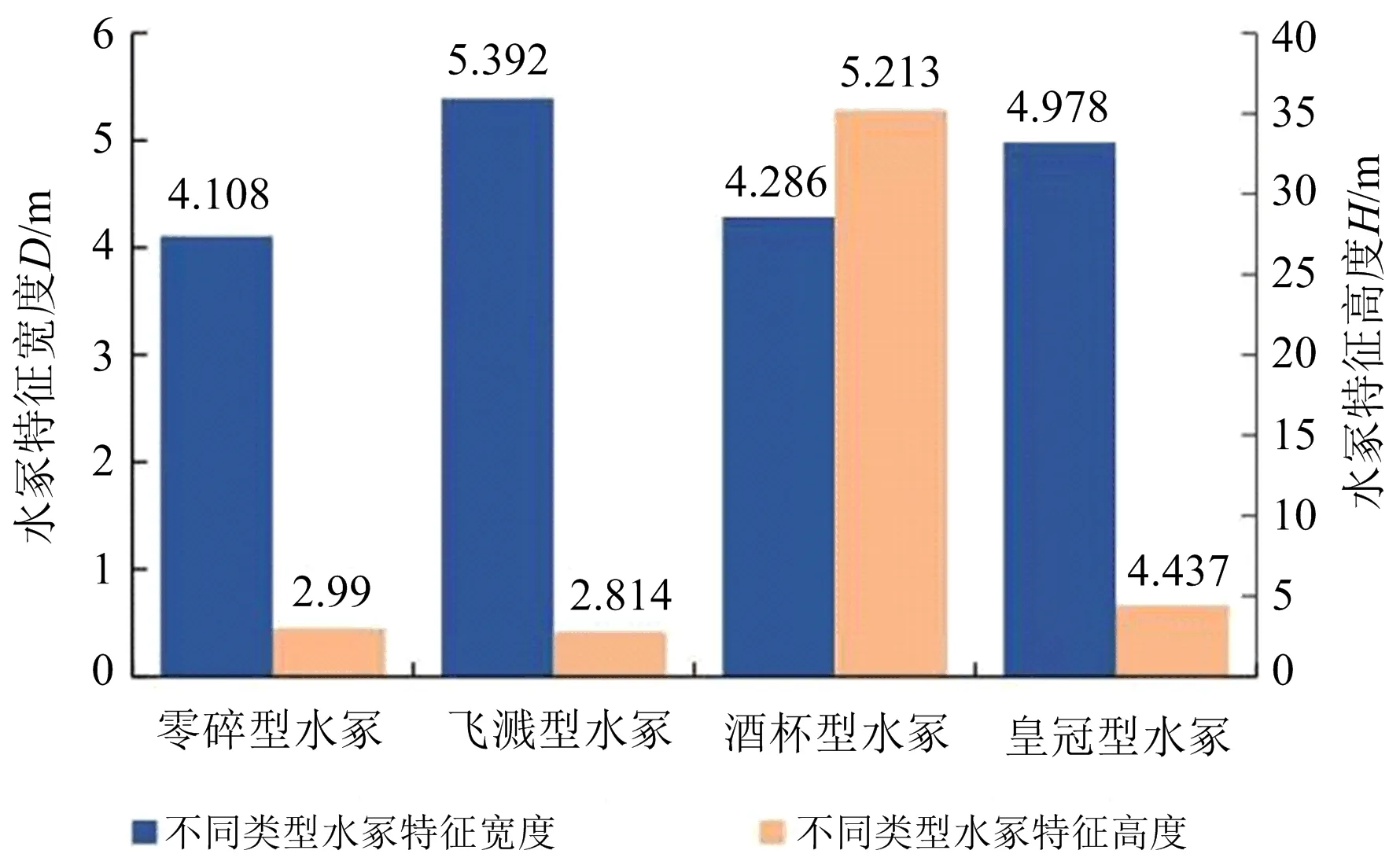
图11 不同类型水冢特征尺寸对比Fig.11 Comparison of the characteristic sizes of different types of water mounds

零碎型和飞溅型水冢的最大宽度是气泡在破碎前形成的空腔直径。飞溅型水冢宽度大于零碎型水冢，这是由于零碎型水冢的起爆水深更浅，气泡会更快速的膨胀到空气中发生破碎。

酒杯型水冢和皇冠型水冢的水冢宽度，主要与气泡进行第二周期脉动推动水面形成的射流位置相关，皇冠型水冢中心水柱的向上速度更低，形成的中心水柱底部宽度更大，使得气泡第二周期脉动形成的环状水体在更靠外侧的位置形成，水冢宽度也因此更大。

对于零碎型水冢和飞溅型水冢的中心水柱高度，形成的主要原因是空腔四周水体在重力作用下向空腔底部汇聚形成的汇聚水柱。由图6c及图7c可知，飞溅型水冢空腔周围水体范围更大，且空腔高度更高，从能量角度分析，飞溅型水冢形成的汇聚水柱应该会比零碎型水冢汇聚水柱更高，但由于飞溅型水冢在空腔顶部形成的交汇向下射流与汇聚水流的运动方向相反，阻碍了汇聚水柱的形成，使得飞溅型水冢形成的中心水柱高度更低，这一现象也体现在飞溅型水冢的汇聚水柱的上下断面宽度基本相同，而零碎型水冢的汇聚水柱为锥形。

对比酒杯型水冢和皇冠型水冢的水柱高度，由图11可知，酒杯型水冢形成的中心水柱高度为35.213 m，皇冠型水冢形成的中心水柱高度仅为4.437 m，两者相差较大。这是由于皇冠型水冢所处位置水深较大，向下气泡射流的剧烈程度相较于酒杯型水冢是偏低的，因此形成的向上射流速度也较低。在向上射流形成的时刻，垂直方向距气泡顶部1 m位置处，皇冠型水冢向上射流速度为9.27 m/s，而酒杯型水冢的向上射流速度为29.8 m/s，同时皇冠型水冢气泡上部水体厚度更大，向上射流要穿透水体进入空气中形成中心水柱所要消耗的能量也更大。综上原因，在皇冠型水冢与酒杯型水冢的工况下虽然都能形成稳定的气泡脉动、射流，但形成的中心水柱高度存在极大的差距。

2.6 不同类型水冢的水面波动特性

水下爆炸引起的水面波动在一定程度上会对水上结构物施加波浪压力，对于类似核弹等超大装药量情况下的水下爆炸，形成的水面波动甚至可以等效为海啸波。根据前文所形成的的水冢，分析不同类型水冢形成的水面波动特性。

距炸药气泡中心5 m处不同形态水冢形成的水面波动如图12所示。对于零碎型水冢的水面波动，水冢形态形成的800 ms以内，由于气泡破碎在100 ms左右已经破碎，自由液面只是在空腔膨胀过程中，水面出现了较低程度的上升。在1 000～2 200 ms左右的液面下降是空腔汇聚水柱开始形成，到2 650 ms汇聚水柱达到最高时刻之间，中心水柱不断升高，四周水体向中心区域流动，在一定的时间延迟之后带动5 m处自由液面下降。自2 650 ms水柱达到最高点之后，在重力作用下汇聚水柱开始冲击水面形成水面波动，并持续向外传播，2 200～4 000 ms水面上升，此时水面最大的上升高度为31.570 cm。

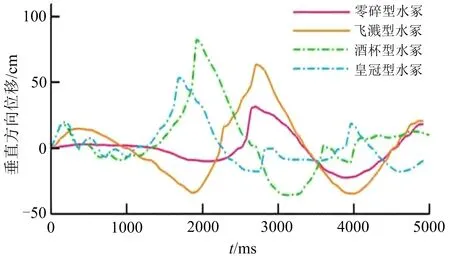
图12 不同形态水冢形成的水面波动时程变化Fig.12 Time-history of water surface fluctuation formed by different forms of water mounds

对于飞溅型水冢的水面波动，在水冢形成阶段，相较于零碎型水冢，飞溅型水冢对水面的影响更加明显，这主要是由于其形成的空腔范围更大，气泡的膨胀带动水体向上运动但并未破碎飞溅，形成了连续的水面隆起，带动了监测点处的自由液面位置上升。在400～1 900 ms之间，监测点处自由液面下降，一方面是由于前一阶段气泡脉动破碎之后水面的隆起消失，更主要的是与零碎型水冢相同，空腔四周水体开始汇聚形成汇聚水柱，带动周围水体向中心汇集，使水面降低。在2 800 ms时刻汇聚水柱达到最大高度，此后开始在重力作用下冲击水面，形成波浪向外传播。监测点处的水面最大上升高度为64.060 cm，大致为零碎型水冢的2倍，虽然飞溅型水柱高度比零碎型水柱高度大0.325 m，两者的体积分别为38.780 m3和15.450 m3，但是飞溅型水冢所具有的重力势能更大，因此冲击水面形成的兴波波浪高度也更大。

对于酒杯型水冢的水面波动，在水冢形成初期，气泡迅速膨胀顶起的水体在气泡收缩阶段的下落形成了初期的水面波动。在400 ms之后，随着中心水柱和四周环形水体的上升，四周水体向中心流动，监测点的水面略微下降。随后四周的环形水体和中心水柱根部附近的大量水体在重力作用下持续冲击水面，形成了较大的水面波动，监测点最高的水面波动位移为83.085 cm。在最高水面波动通过监测点后，可以看到后续出现一个小的水面波动，以及一个持续的水面上升过程，则是残余的部分环状水体和部分下落的中心水柱冲击水面形成的残余水面波动。

对于皇冠型水冢的水面波动，与酒杯型水冢类似，在水冢形成初期，气泡膨胀顶起的水面下坠形成了一定程度的水面波动。伴随着水冢的形成，四周水流向中心流动，使得监测点处自由液面出现一定程度的下降。随后在中心水柱和四周环状水体形成的水冢下坠冲击下，自由液面形成波动。皇冠型水冢在监测点处形成的最大水面波动位移为53.640 cm，相对酒杯型水冢较低，形成该现象的原因一方面是由于中心水柱的高度更低，仅为4.337 m。另一方面是由于气泡多次脉动形成的自由液面破碎情况更加剧烈，后续的环状水体与之前形成的环状水体相互冲击消耗了能量。从图3中可以观察到在最高水面波动通过监测点之后，还形成了两个小的水面波动，前者是部分残余的环状水体冲击水面形成的，后者是后续中心水柱上部水体冲击水面形成的。