隧道下穿引起既有管道竖向位移的简化计算方法
2021-09-06管凌霄徐长节可文海马锡海徐立明虞巍巍
管凌霄,徐长节,2,可文海,马锡海,徐立明,虞巍巍
(1.华东交通大学 江西省岩土工程基础设施安全与控制重点实验室;土木工程国家实验教学示范中心,南昌 330013;2.浙江大学滨海和城市岩土工程研究中心,杭州 310058;3.浙江航海城际铁路有限公司,浙江 嘉兴 314000;4.中交一公局集团有限公司,北京 100037)
城市地铁盾构隧道开挖导致的地层损失会引起周围地层的变形[1],由于城市地下存在大量的管道,紧邻管道的盾构施工必然对其产生重大影响。因此,众多学者对如何准确分析盾构隧道下穿施工对邻近管道的影响展开了研究[2]。

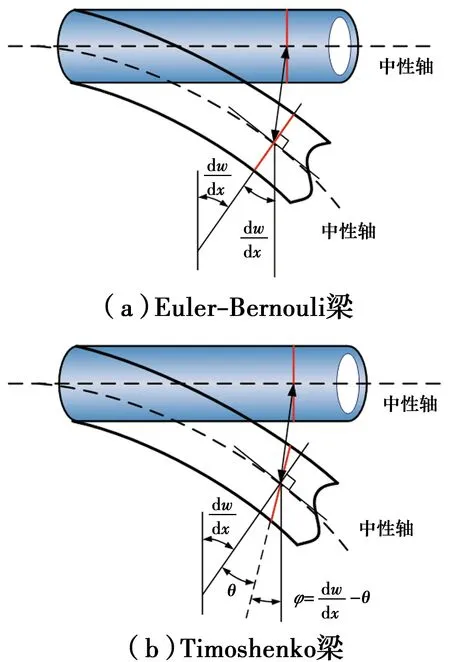
图1 Euler-Bernoulli梁与Timoshenko梁变形特征

1 基本方程的建立
1.1 土体自由场竖向位移
土体自由场竖向位移采用Loganathan等[13]基于线弹性理论提出的盾构隧道开挖引起周围土体自由场竖向位移的计算方法进行计算,根据该方法,土体自由场竖向位移Uf(x,z)为
(1)
式中:x为距隧道轴线的水平距离;z为距地表的垂直距离;ε0为盾构隧道开挖引起的平均地层损失比;R为隧道半径;H为隧道轴线与地表的垂直距离;v为土体泊松比。采用的简化计算模型如图2所示,图中z0为管道轴线与地表的垂直距离,D为管道直径。此时,管道轴线z=z0处因盾构隧道开挖引起的土体竖向位移可表示为Uf(x)=Uf(x,z0)。
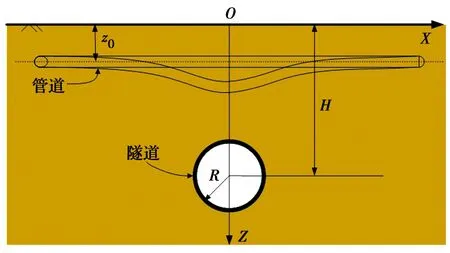
图2 简化计算模型
1.2 管道控制方程的建立

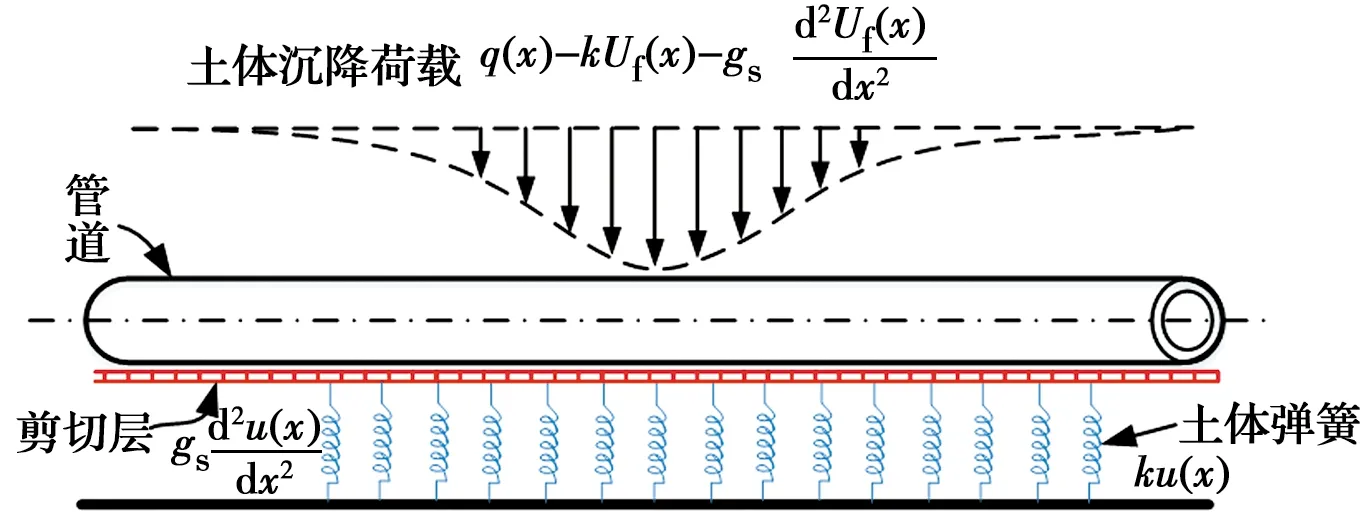
图3 管土相互作用模型
p(x)Ddx-q(x)Ddx-dQ=0
(2)
(3)
式中:Q、M为管道单元受到的剪力及弯矩;q(x)为土体位移产生的荷载;p(x)为地基反力。根据Pasternak地基模型可得q(x)、p(x)为
(4)
(5)
式中:w(x)为管道位移函数;k为地基弹性系数;gs为地基剪切系数。k与gs可由式(6)、式(7)计算[14-15]。
(6)
(7)
式中:Es土体弹性模量;EpIp为管道的抗弯刚度;t为土体剪切层厚度,根据文献[16],对于管线这种长宽比很大的地下结构,当地基深度大于结构宽度的6倍时,其地基土的附加应力已衰减至非常小,因此,取t=6D进行计算。
根据Timoshenko梁理论,当管道产生竖向变形时,其弯矩M、剪力Q与竖向位移w(x)的关系为
(8)
(9)
式中:κGA为管道等效剪切刚度;κ为管道等效截面系数,管道为环形截面,故取0.5;G为管道剪切模量,G=Ep/2(1+vp),vp为管道泊松比;A为管道的横截面面积。
将式(4)、式(5)、式(8)、式(9)代入式(2)、式(3)可得管道位移w(x)的控制方程为
(10)
2 管道控制方程的求解
式(10)为四阶微分方程,公式复杂不便于直接求解。为方便进行推导,可先求出Pasternak地基上Timoshenko无限长梁在集中力作用下的解。先令q(x)=0,整理式(10)并求通解,可得
w(x)=eαx[C1cos(βx)+C2sin(βx)]+
e-αx[C3cos(βx)+C4sin(βx)]
(11)
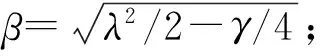
假设管道为Pasternak地基上无限长的Timoshenko梁,在x=0的原点上受到一集中荷载P,此时x=0处的管道截面因为位于集中力正下方,受力后未发生旋转仍垂直于中性轴,因此,管道的边界条件可为
w(±∞)=0
(12a)
φx=0=0
(12b)
Qx=0=PD/2
(12c)
将边界条件式(12)代入式(11)中,可推导得到无限长Timoshenko模型管道在集中荷载P作用下的位移方程为
(13)
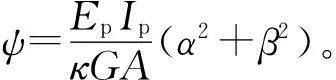
由文献[17]可知,为推导出管道受分布力作用下的位移控制方程式(10),可根据集中荷载作用下的位移控制式(13)进行叠加。整理式(10),可得
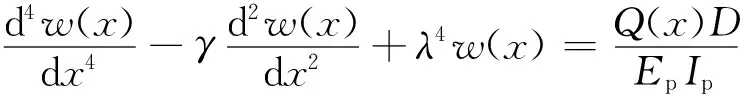
(14)
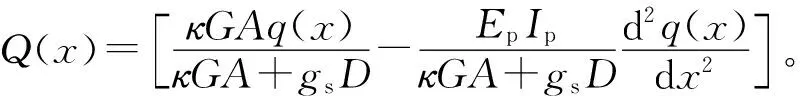
由此可知,盾构隧道开挖时,Timoshenko梁管道在轴线上的任意一点ξ受到的附加荷载为
(15)
将式(15)代入式(13),可得到下列该点荷载引起的管道竖向位移dw(x)为
(16)
对式(16)在盾构隧道开挖引起土体竖向位移的范围内积分,即可求得考虑管道剪切效应时的管道竖向位移
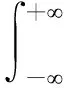
(17)
3 算例验证
3.1 工程算例1
采用文献[18]中盾构隧道下穿开挖对邻近管道影响实例的管道竖向位移监测数据对该方法进行验证。实例中地铁盾构隧道垂直下穿一条混凝土电缆管道,管道的泊松比vp=0.17,厚度T=0.12 m,其余物理参数参考文献[8]取值,如表1所示。

表1 管道计算参数
图4为该方法计算结果与实测值以及文献[8]计算结果的对比。文献[8]采用Pasternak地基模型与Euler-Bernouli梁模型模拟管道位移,由图4可见,采用Pasternak地基模型与Timoshenko梁模型的计算方法所得管道位移曲线与实测值更加吻合,同时,与文献[6]考虑管道侧向土体作用时的结果基本一致,证明了该计算管道竖向位移所用方法的准确性。
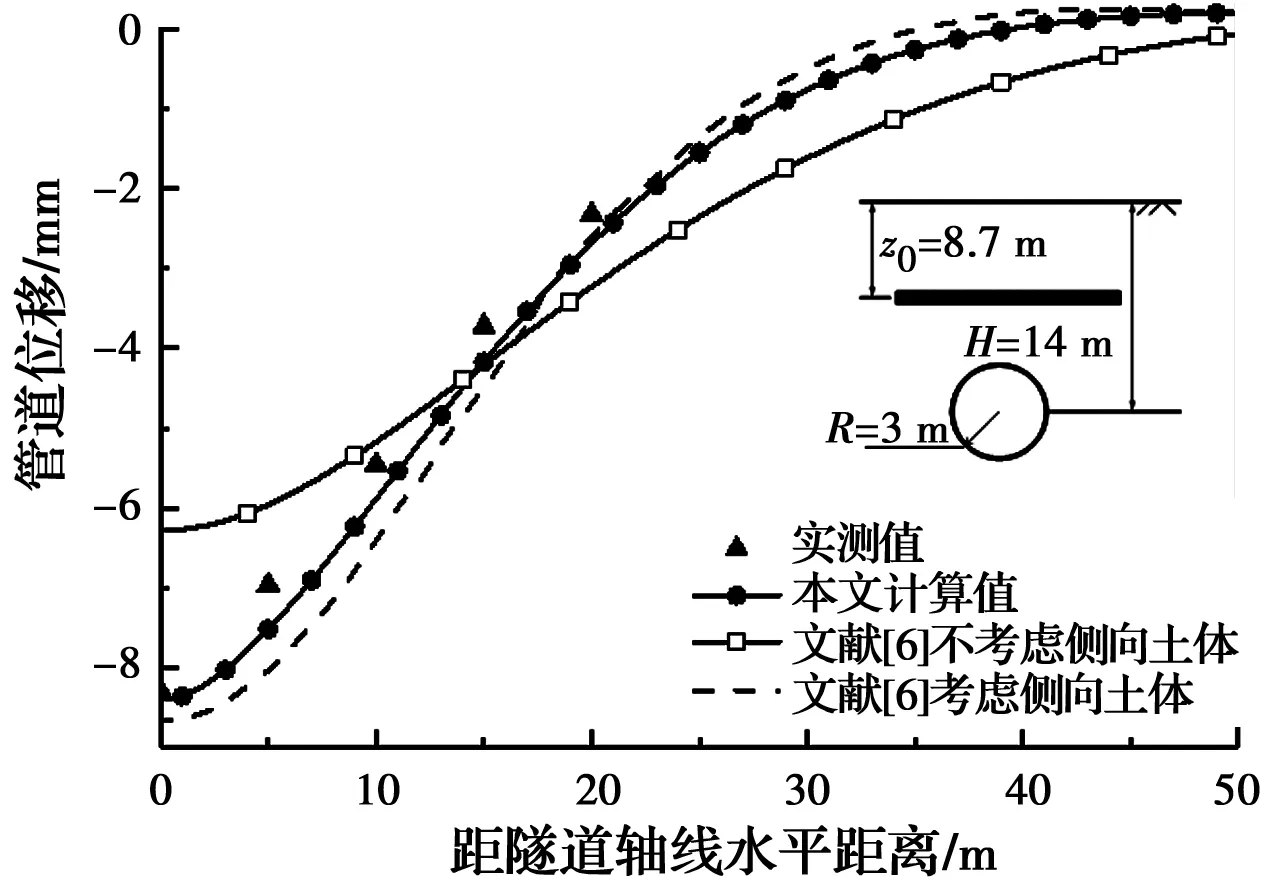
图4 不同求解方式的管道位移
3.2 工程算例2
Vorster等[4]使用剑桥大学的离心机进行了盾构隧道开挖对邻近管道影响的试验研究。该离心机试验中的加速度为75g,文献[19]对1g加速度下的物理参数进行取值:隧道半径R=2.25 m;轴线埋深H=11.25 m;地层损失率ε0=2%;管道抗弯刚度EpIp=3.363×106kN·m2;根据管道材质为铝合金,且保证抗弯刚度取管道弹性模量Ep=57.5 GPa,泊松比vp=0.3,直径D=1.19 m,轴线埋深z0=4.165 m;土体弹性模量Es=19.52 MPa,由于土的泊松比很难精确得到,因此,根据砂土的近似泊松比取v=0.25。
该计算方法的计算结果与离心机模型试验结果对比如图5所示。由图5可以看出,该方法计算所得管道最大竖向位移值为22.40 mm,略小于试验所得25.08 mm,总体结果较为一致,呈现的规律基本吻合,进一步验证了该方法的准确性。
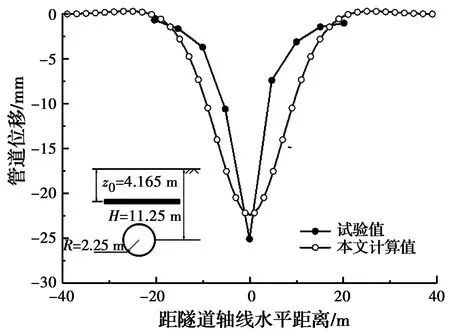
图5 与离心机试验对比图
4 参数分析
为研究各物理参数变化对考虑剪切效应的管道竖向位移的影响,取如下算例进行分析:其中,盾构隧道的物理参数为:轴线埋深H=15 m、半径R=3 m、地层损失率ε0=1%;管道物理参数为:直径D=2 m、管片厚度t=0.12 m、弹性模量Ep=3×104MPa、轴线埋深z0=5 m、泊松比vp=0.2;土体物理参数为:弹性模量Es=6 MPa、泊松比v=0.3。在分析某一参数与管道竖向位移的关系时,其余参数不变。
4.1 管土弹性模量比变化对管道竖向位移的影响
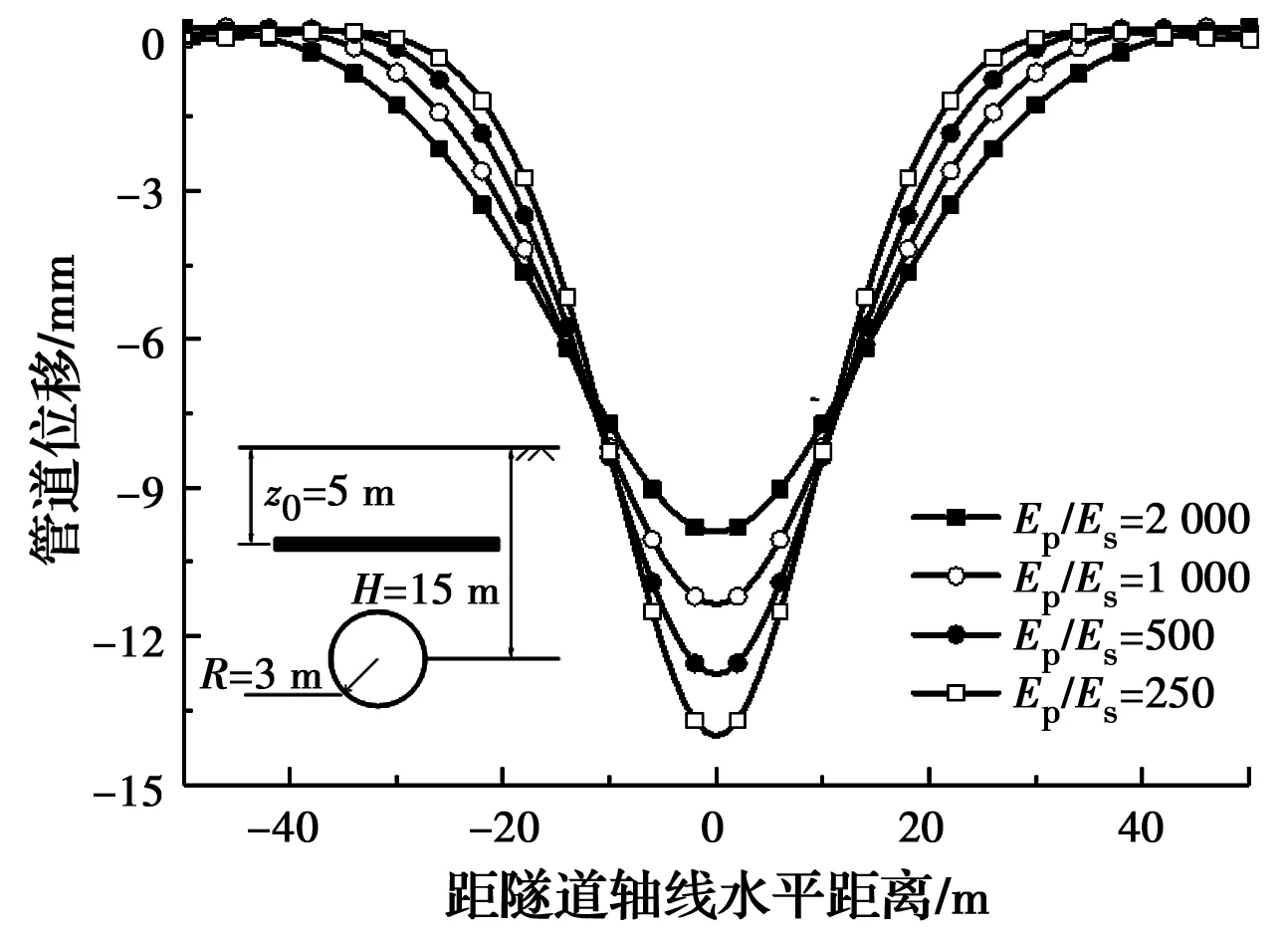
图6 不同管土弹性模量比对应的管道竖向位移
4.2 管道直径变化对管道竖向位移的影响

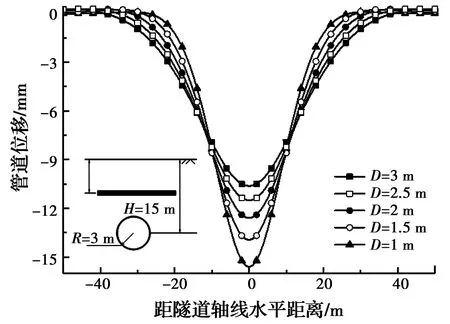
图7 不同管道直径对应的管道竖向位移
4.3 管道剪切刚度变化对管道竖向位移的影响
为研究考虑剪切效应时管道竖向位移与管道剪切刚度之间的关系,取4组管道剪切刚度进行分析,分别为10、1、0.1、0.01 κGA。
图8为不同管道剪切刚度的情况下,考虑剪切效应时盾构隧道下穿施工引起的管道竖向位移曲线。从图8可看出,在管道剪切刚度从10 κGA减小到0.01 κGA时,管道竖向位移的最大值随之增大,由此可说明管道剪切刚度的变化对管道竖向位移存在影响。同时,随着剪切刚度的减小,管道竖向位移最大值增大的幅度迅速增加,因此,在一定的剪切刚度范围内,不应忽略管道的剪切变形,尤其对于剪切刚度较小以及可能存在纵向裂缝等病害的管道,采用Timoshenko梁模型模拟管道会更加合理。
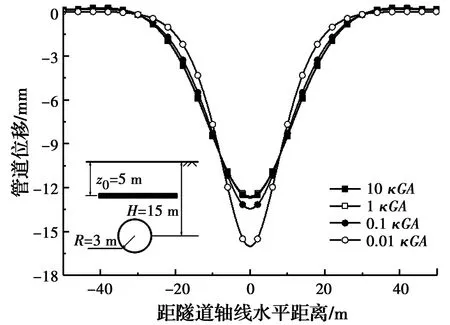
图8 不同管道剪切刚度对应的管道竖向位移
5 结论
采用两阶段分析法推导了考虑管道剪切效应时盾构隧道开挖引起邻近管道竖向位移的解析解。在第2阶段采用考虑剪切效应的Timoshenko梁模型模拟管道并结合叠加法提出了简化算法,经过深入分析,得到以下主要结论:
1)采用考虑剪切效应的Timoshenko梁模型研究盾构隧道下穿开挖对邻近管道竖向位移分析时,其计算结果较Euler-Bernouli梁模型更为准确,结合叠加法进行求解的计算结果准确且便于推导。
3)其余参数一定时,管道剪切刚度的减小可导致管道最大竖向位移值增大,对于剪切刚度较小以及可能存在纵向裂缝等病害的管道,采用Timoshenko梁模型模拟管道更加合理
