桩基三维非对称局部冲刷坑条件下土体应力计算简化模型
2021-09-06王增亮周航丁选明吴岱峰蔡汝一肖治微
王增亮,周航,丁选明,吴岱峰,蔡汝一,肖治微
(1.重庆大学 山地城镇建设与新技术教育部重点实验室;土木工程学院,重庆 400045;2.重庆市城市建设投资(集团)有限公司,重庆 400023)
桥梁作为供公路、渠道、铁路、管线等跨越库区、山谷、河流等其他交通线最常用的工程结构,在经济建设和社会发展中发挥着举足轻重的作用。深水桩基础是现代桥梁建设最主要的基础形式之一,具有体积大、阻水面积大的特点。由于深水桩基础所处的水环境非常复杂,在长期的河流冲刷作用下,桩基础周围土体被掏空,导致桩基承载力下降,从而使桥梁、公路发生破坏。董正芳等[1]收集了典型的502座桥梁倒塌事故,发现洪水和冲刷造成的桥梁毁坏事故最多。Lagasse等[2]通过统计指出,由冲刷引起的桥梁损坏事故约占60%。同时,其他学者[1, 3-5]的研究表明,冲刷是造成桥梁失效的主要原因。
桥梁桩基冲刷形式按中国分类标准分为长期冲刷(一般冲刷)、收缩冲刷以及局部冲刷。与一般冲刷相比(整个河床的自然冲刷),局部冲刷通常发生在桩基础、桥墩、桥台以及其他过水障碍物处,因此,局部冲刷只发生在桩周附近上覆土层[6-7],造成桩基有效埋深减小。Fischenich[8]指出桩周局部冲刷深度可达到河床一般冲刷深度的10倍。在桩基局部冲刷设计中,有部分学者将局部冲刷深度以上土体全部移除,即将局部冲刷简化为一般冲刷参与桩基设计计算,此种简化方式会使桩基设计过于保守,使桩基承载力不能充分发挥,造成建筑资源的大量浪费。基于此,有规范将局部冲刷坑简化为一个倒截头的圆锥[9-10],Richardson等[11]指出,局部冲刷坑的坡角为河床物质的休止角,其值在30°~45°之间。在海洋等部分环境中冲刷坑多为这种形态。因此,目前桥梁桩基冲刷方面的设计和研究主要关注桩周形成对称形态的冲刷坑时,桩基轴向和侧向承载力的计算问题[12-15]。然而,在库区河道以及河流桩基环境中,桩周形成的局部冲刷坑多为非对称的,具体表现为桩基上游冲刷深度大、冲刷坡度较大,桩基下游冲刷深度小、冲刷坡度也较小[16-17]。在桩周形成非对称冲刷坑时,采用倒截头圆锥形态的冲刷坑参与设计计算,即忽略桩基受到的水平应力的影响,显然会与实际相差较大。例如,实际工程中,桩周形成非对称冲刷坑时,冲刷小的一侧土体对桩基的水平作用力要大于冲刷较为严重的一侧。桩基在受到两侧不等的水平作用力时,使桩基产生较大的挠曲变形和弯矩,当桩基上部荷载较大时,桩基的挠曲变形会显著增加。然而,目前关于桩周形成非对称冲刷坑时桩周土体应力计算及其对桩基影响的研究较少。开展非对称冲刷坑条件下桩周土体应力计算的研究,可以为桩基设计提供相关的理论依据,也具有一定的实际和学术研究意义。
桩周形成局部冲刷坑时,关于桩周土体应力的计算,笔者回顾了3种目前被广泛应用于桩基设计规范的方法,即API、FHWA-DP(FHWA driven piles)以及FHWA-DS(FHWA drilled shafts)中建议的方法。其中,FHWA-DP中假设桩周土体应力不受局部冲刷的影响,即土体应力计算时按未发生局部冲刷条件下的河床表面进行计算[18],在局部冲刷较为严重的工程中,FHWA-DP的应力计算方法显然与实际不符,使设计的桩基以及上部结构处于不安全状态。此外,API和FHWA-DS通过引入影响深度的概念来计算局部冲刷引起的桩周土体有效应力的损失。即影响深度以上土体有效应力线性减小,影响深度以下桩周土体有效应力与未发生局部冲刷一致。可以看出,API和FHWA-DS中建议方法弥补了FHWA-DP中方法的不足,但API和FHWA-DS中计算方法只适用于固定形态的冲刷坑。如FHWA-DS适用于冲刷坑底部宽度为0、冲刷坡角为26.6°、冲刷深度可变的工程条件[19],API适用于冲刷深度为1.5倍的桩径、冲刷坑底部宽度为0、冲刷坡角固定的条件,且规范中并未指定冲刷坡角的大小[20]。然而,实际工程中,冲刷坑形态并非固定形态,因此,这3种建议方法有很大的局限性。在此基础上,Lin等[21-22]基于Boussinesq解得到了可以考虑冲刷深度、冲刷坑顶部宽度、冲刷坑底部宽度及冲刷坡角可变的桩周土体应力计算解析解。使得局部冲刷坑条件下桩周土体应力计算更加符合工程实际,该解析解只适用于计算对称冲刷坑形态的桩周土体垂直有效应力。对于库区河道环境,桩周形成非对称局部冲刷坑时的工程状况并不适用。笔者根据实际工程调查以及室内试验得到的非对称局部冲刷坑形态,提出了非对称冲刷坑的简化模型,并给出了桩周形成非对称冲刷坑时的土体应力计算方法。主要思路为:根据试验及工程实际中非对称冲刷坑的横、纵截面形态,提出了非对称冲刷坑的简化模型,在此基础上,假设非对称冲刷坑最大冲刷深度以上土体重度为外荷载并引起了冲刷坑深度以下土体产生附加应力,基于Boussinesq解的严格定义及适用条件,假设桩径为0,得到冲刷深度以下土体的垂直和水平附加应力。通过与最大冲刷深度以下土体应力的叠加,得到非对称冲刷坑内土体应力值,并通过有限元计算结果进行对比验证,在此基础上考虑桩径的影响。通过与有限元计算结果的对比验证,探讨了有桩时桩周土体应力计算的正确性。最后,对简化模型的参数进行了敏感性分析。
1 非对称冲刷坑条件下土体应力计算理论模型
Butch等[17]研究指出,非对称局部冲刷坑呈现出桩基上游冲刷坑冲刷深度大、冲刷坡角大,桩基下游冲刷坑冲刷深度小、冲刷坡角小的形态。Diab[16]通过大型模型槽试验得到的圆桩桩周非对称局部冲刷坑随时间变化的横、纵截面图如图1所示。基于此,笔者提出的三维非对称局部冲刷坑简化模型图如图2所示。图3为简化模型剖面图与平面图。

图1 非对称局部冲刷坑纵向和横向剖面图[16]

图2 三维非对称局部冲刷坑简化模型图
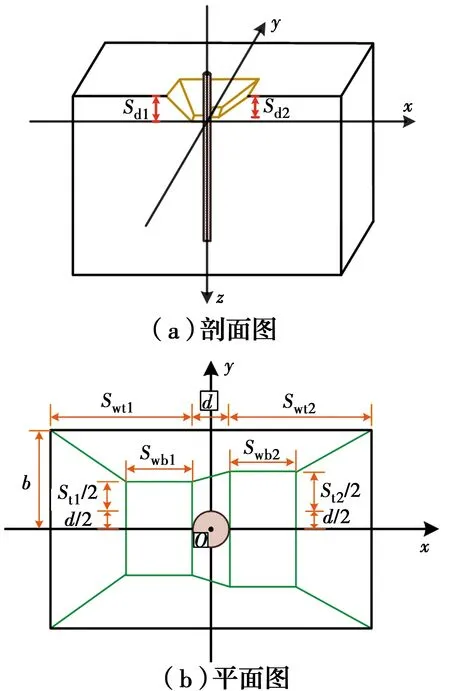
图3 非对称局部冲刷坑简化模型剖面图和平面图
简化模型中用以表征非对称局部冲刷坑的几何参数包括:桩基上游顶部长度Swt1、桩基上游底部长度Swb1、桩基上游底部宽度St1、冲刷坑宽度2b、桩基下游顶部长度Swt2、桩基下游底部长度Swb2、桩基下游底部宽度St2、桩基上游冲刷深度Sd1、桩基下游冲刷深度Sd2、桩基上游冲刷坑坡度β1、桩基下游冲刷坑坡度β2以及桩基两侧坡度β3,由于简化模型关于xoz平面对称,为了便于计算,采用一半模型参与计算,在图3(b)中也只标注了一半模型的几何尺寸。
同时可以发现,用以表征非对称局部冲刷坑的几何参数间存在如式(1)~式(4)所示关系。
(1)
(2)

(3)
(4)
如图3(a)所示,假设xoy平面以上土体重度为外荷载(局部冲刷坑最大冲刷深度以上未冲刷土体),并在xoy平面任意深度处产生垂直附加应力项Δσz、水平附加应力项Δσx,则xoy平面以下为半无限空间地基。根据Boussinesq解,桩周土体的垂直和水平附加应力计算用式(5)、式(6)表示。
(5)
(6)
式中:R=(x2+y2+z2)1/2。
1.1 非对称冲刷坑下垂直有效应力(σz′)计算
非对称局部冲刷坑下,桩周土体垂直有效应力计算分为两部分:第1部分为xoy平面以下土体的垂直有效应力,第2部分为xoy平面以上土体产生的附加应力项。对式(5)在x、y方向上进行分段二重积分即可得到任意深度z处垂直方向上的附加应力项。具体如式(7)~式(21)。
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)


则可以得到非对称冲刷坑内桩周任意深度z处的垂直有效应力,可表示为
σz′=2Δσz′+γ′z
(22)
式中:Δσz为以上各分量的叠加。
1.2 非对称冲刷坑下水平有效应力σx′计算
非对称冲刷坑条件下桩周土体水平有效应力计算也分为两部分:第1部分为xoy平面以下土体水平有效应力部分,该部分按静止土压力理论参与计算,第2部分为xoy平面以上土体重度引起的附加应力项,通过Boussinesq解在x、y方向分段进行二重积分得到。具体如式(23)~式(34)。
(23)
(24)
(25)
(26)
(27)
(28)
(29)
(30)
(31)
(32)
(33)
(34)
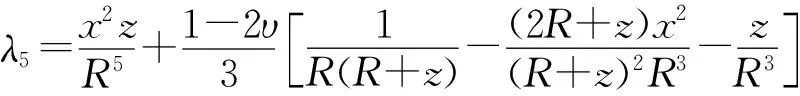
由此,得到非对称冲刷坑条件下桩周任意深度z处土体的水平有效应力,可表示为
σx′=2Δσx′+K0γ′z
(35)
式中:K0=υ/(1-υ)为静止土压力系数;γ′为土的有效重度。
2 模型验证
为验证提出的非对称冲刷坑内土体应力计算模型的正确性,验证中忽略桩径的影响(即d=0),符合Boussinesq解的严格使用条件。土体垂直及水平有效应力计算公式如式(35)、式(36)。用MATLAB软件对计算公式进行数值积分并与ABAQUS数值计算结果进行对比验证。由于冲刷坑模型关于平面对称,因此,ABAQUS模拟时选取坑体模型的一半进行分析。在ABAQUS数值模型中采用“生死单元法”来模拟冲刷坑的形成。具体分为两个分析步:第1个分析步为地应力平衡分析步,第2个分析步采用“生死单元”杀死局部冲刷坑内的土体模拟被冲刷的土体。数值模型中冲刷坑的几何参数见表1,表1中坑体参数由Diab试验数据等比放大得到,土的弹性模量为80 MPa,泊松比υ=0.3,土体的有效重度γ′=10.4 kN/m3,ABAQUS模型如图4所示,模型长度为35 m、宽度为16 m、高度为15 m。

图4 有限元计算模型图

表1 非对称冲刷坑参数
σz′=2(Δσz3′+Δσz4′+Δσz5′+Δσz6′+
Δσz7′+Δσz8′+Δσz9′+Δσz10′+
Δσz13′+Δσz14′+Δσz15)′+γ′z
(36)
提出的简化模型的计算结果与有限元冲刷模拟的计算结果对比如图5所示,图5(a)为冲刷坑中心位置处垂直有效应力对比图,图5(b)为水平有效应力对比图。通过与未冲刷时土体内部垂直有效应力的对比发现,冲刷坑形成后减小了土体的垂直有效应力,且这种减小趋势只出现在一定深度范围内,这与FHWA-DS、API以及Lin等[19-22]的结论一致。同时可以看出,提出的理论计算结果与有限元计算结果具有较好的一致性。从而验证了提出的非对称冲刷坑内运用Boussinesq解计算土体应力的正确性和可靠性。

图5 本文解与有限元计算对比
3 考虑有桩条件下土体应力计算适用性探讨
提出的计算模型是基于严格定义在半无限地基中Boussinesq点荷载方程得到的,在应用Boussinesq方程时忽略了桩径的影响。该部分引入桩径的影响,即d≠0时,通过与有限元计算结果进行对比验证,从而探讨考虑冲刷坑内存在桩时桩周土体应力计算的适用性和可行性。由于有限元计算模型关于平面对称,故采用模型的一半进行分析,如图6所示。ABAQUS有限元数值模型分为两个分析步进行计算:第1个分析步为地应力平衡分析步,第2个分析步采用“生死单元法”模拟桩周冲刷坑的形成。模型的参数为:土体的弹性模量为80 MPa、泊松比υs=0.3、土体的有效重度γ′=10.4 kN/m3、桩的弹性模量为20 GPa、桩径为1.8 m、泊松比为υp=0.2、桩长为14 m、模型长度为54 m、宽度为27 m、高度为23 m,因此,可以忽略边界效应的影响。模型所采用的坑体参数如表2所示、有限元模型底部约束3个方向的位移、4个侧面分别约束x、y方向的位移。由于模型中桩基的存在,模型得到的土体垂直有效应力为桩周土体的垂直有效应力值,提出的计算模型中桩基上、下游侧土体水平有效应力分别按式(37)、式(38)计算。
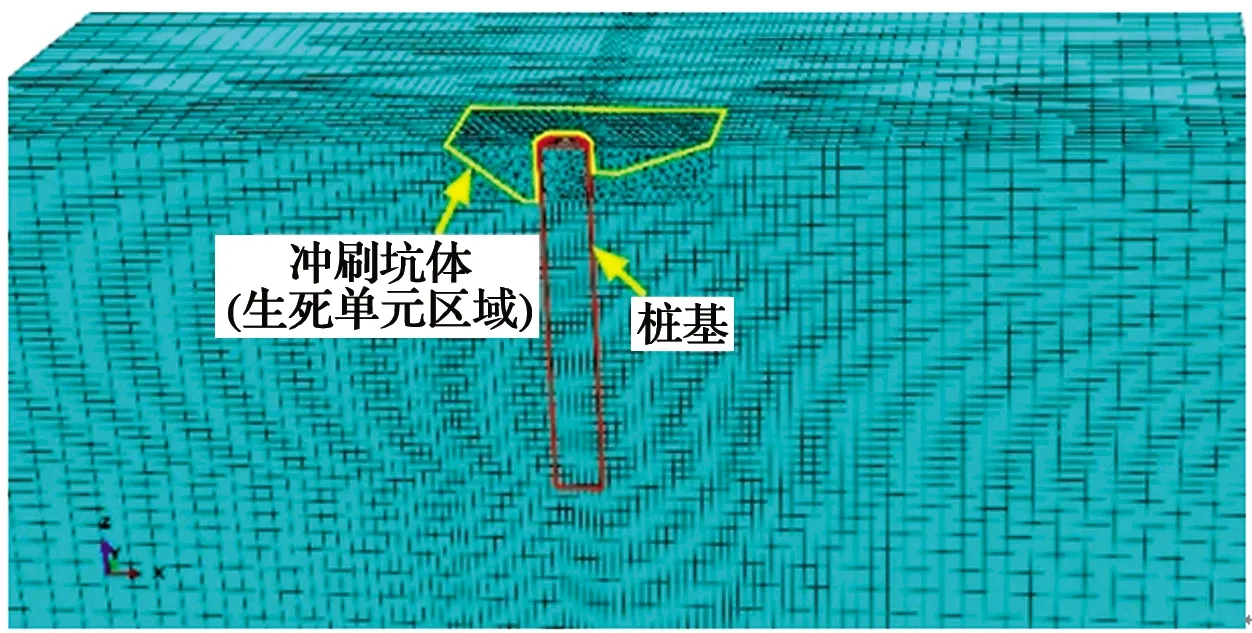
图6 有桩时有限元计算模型

表2 有桩条件下非对称冲刷坑参数
σx-上游′=2(Δσx5′+Δσx7′+Δσx8′+
Δσx9′+Δσx10′)+K0γ′z
(37)
σx-下游′=2(Δσx1′+Δσx2′+Δσx3′+Δσx4′+
Δσx6′+Δσx11′+Δσx12′)+K0γ′z
(38)
图7为非对称冲刷坑内有桩时理论计算结果与有限元计算结果对比图,提出的计算模型的结果由MATLAB软件进行数值积分得到,有限元计算结果提取的是桩周土体的垂直有效应力以及桩基上、下游土体的水平有效应力。图7(a)为非对称冲刷坑内土体垂直有效应力对比曲线,图7(b)、(c)分别为桩基上下游土体水平有效应力结果对比图。可以看出,提出的土体应力计算模型结果与有限元计算结果表现出较好的一致性。因此,简化模型用来计算非对称冲刷坑内土体的垂直有效应力以及桩基上、下游土体的水平有效应力是可行的。

图7 有桩时本文解与有限元对比
4 参数分析
由简化模型可以看出,非对称冲刷坑计算模型中的独立变量有9个:Swt1、Swb1、Sd1、Sd2、Swt2、Swb2、d、b、St1。为便于探讨各独立变量对非对称冲刷坑内土体应力的影响大小,此部分围绕9个独立变量设计了部分工况,进行了参数敏感性分析。
4.1 不同参数下冲刷坑内桩周土体垂直有效应力变化分析
为便于进行垂直有效应力的参数分析,此处引入垂直有效应力率(式(39))来分析非对称局部冲刷坑形成后桩周土体垂直有效应力的变化。
(39)
式中:σz0′为未冲刷时xoy平面以下的垂直有效应力。
图8~图16为非对称局部冲刷坑模型中9个独立变量对桩周土体垂直有效应力变化规律的影响关系图,参与计算的土体有效重度γ′=10.4 kN/m3。由图8可看出,桩周土体垂直有效应力率随着深度的增加逐渐增大,深度10 m以下时,有效应力率的值趋近于1,说明局部冲刷坑对桩周土体垂直有效应力的影响在一定深度以内,影响深度以下时土体垂直有效应力与未冲刷时保持一致。当桩基上游顶部冲刷长度Swt1从3 m到7 m逐渐增加时,同一深度处Swt1的值越大,土体垂直有效应力率的值越小;深度逐渐增大时,不同Swt1曲线之间的差异呈现出先增大后减小的现象,深度4~10 m范围内上游冲刷长度Swt1对土体垂直有效应力率的影响最大。图9为桩基上游底部冲刷长度Swb1对冲刷坑内桩周土体垂直有效应力率的影响关系曲线。可以看出,同一深度处土体垂直有效应力率随着Swb1值的增大而逐渐减小,然而这种变化趋势不明显,即Swb1值对土体垂直有效应力率的影响较小,在深度12 m处土体垂直有效应力率达到0.98。图10为桩基下游顶部冲刷坑长度Swt2影响下土体垂直有效应力率变化关系曲线。可以看出,同一深度处Swt2从3~7 m逐渐增大时,土体垂直有效应力率呈现出减小的现象,但减小值较小,在深度15 m时,土体垂直有效应力率值趋近于1。图11表明,土体垂直有效应力率受桩基下游冲刷坑底部宽度的影响较小,深度15 m以下时土体垂直有效应力与未冲刷时应力值一致。由图12可知,冲刷坑以下1.5 m深度范围内,同一深度处土体垂直有效应力随桩基上游冲刷深度Sd1的增大而增大,深度大于1.5 m时呈现出变化规律相反的现象。分析其原因为,冲刷坑深度增大时,冲刷坑底以上剩余土体(冲刷坑深度范围内未冲刷土体)对坑底以下浅层土体的影响越大,且冲刷坑深度越大对坑底以下土体垂直有效影响深度越深。由图13可以看出,桩基下游冲刷深度Sd2增加过程中,同一深度处土体垂直有效应力率呈现出减小的现象,该现象在冲刷坑底浅层范围内变化明显,且Sd2值越大其影响深度越深。图14为桩基上游冲刷坑底部宽度变化时的土体垂直有效应力率变化关系曲线。St1的增加对应于冲刷坑两侧坡度β3的增大,可以看出,冲刷坑两侧坡度β3增大时同一深度处土体垂直有效应力率减小且影响深度增大,在深度3~9 m范围内对土体垂直有效应力率的影响最大。图15给出了冲刷坑宽度增加时的土体应力变化关系曲线,由图15可以看出,冲刷坑宽度的变化对冲刷坑底以下土体的垂直有效应力值影响较为明显。在冲刷坑底深度3~11 m范围内不同曲线之间的差异较其他深度处更为明显,深度12 m以下不同曲线趋于重合且接近于1。图16为考虑三维非对称冲刷坑内桩径变化时的土体垂直有效应力率变化规律曲线图。由图16可以看出,冲刷坑形态不变时,土体垂直有效应力率随桩径的增大逐渐减小,然而这种减小趋势不明显,即桩径的大小对冲刷坑以下土体的垂直有效应力的影响较小。
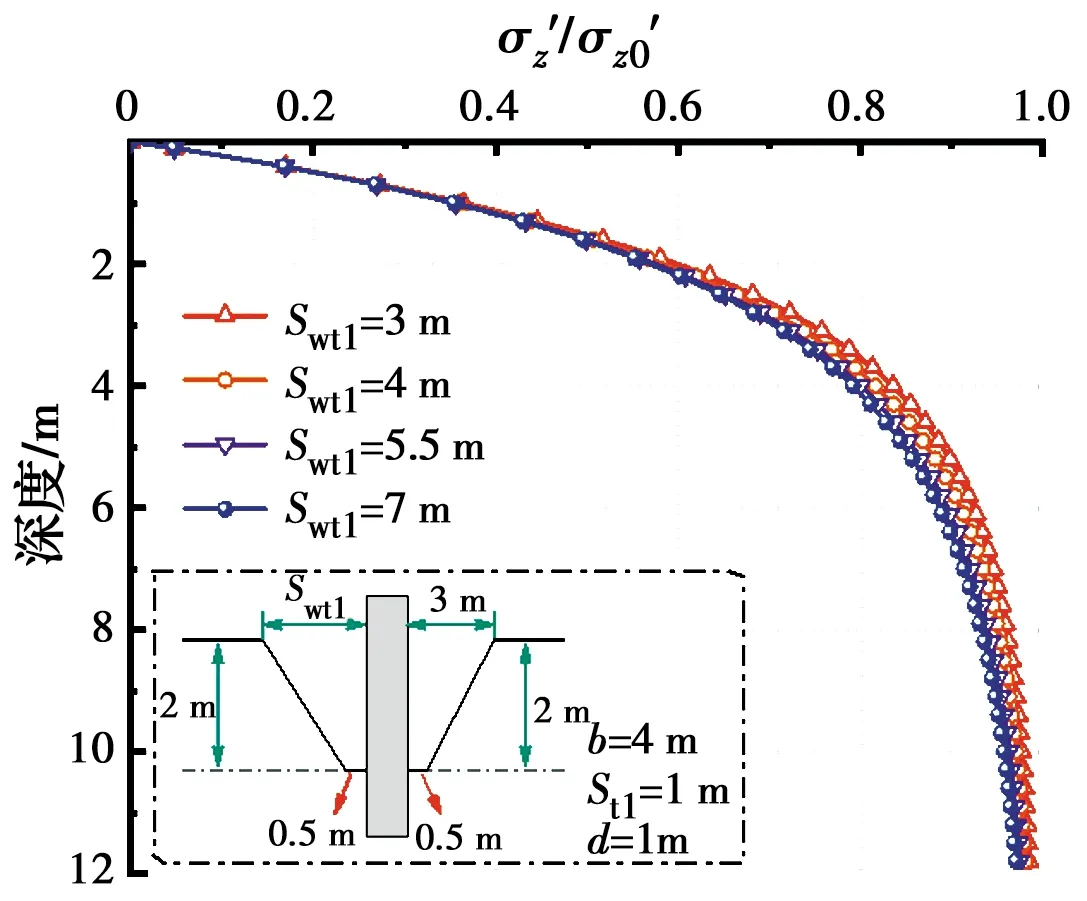
图8 不同Swt1下垂直有效应力率随深度的变化曲线

图9 不同Swb1下垂直有效应力率随深度的变化曲线
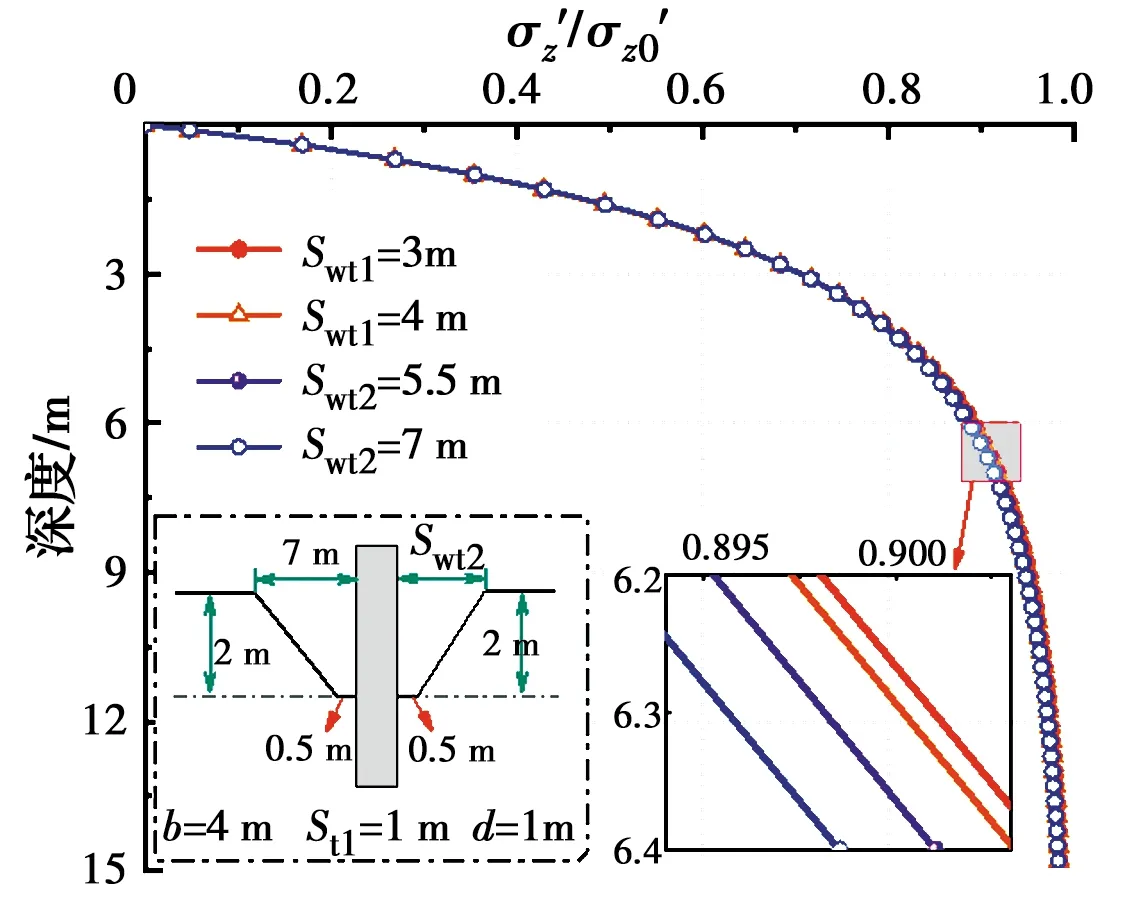
图10 不同Swt2下垂直有效应力率随深度的变化曲线

图11 不同Swb2下垂直有效应力率随深度的变化
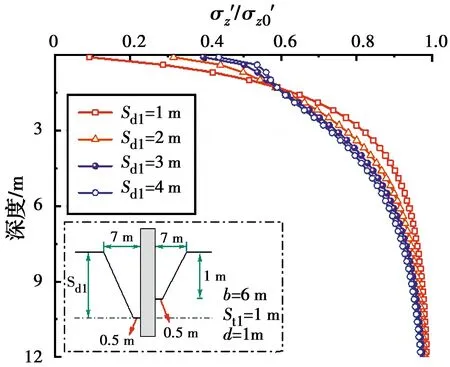
图12 不同Sd1下垂直有效应力率随深度的变化
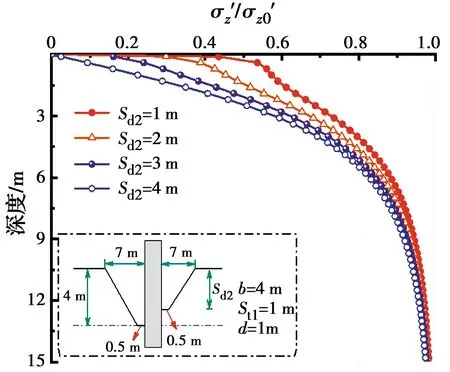
图13 不同Sd2下垂直有效应力率随深度的变化

图14 不同St1下垂直有效应力率随深度的变化

图15 不同b下垂直有效应力率随深度的变化

图16 不同d下垂直有效应力率随深度的变化
4.2 不同参数下冲刷坑内桩周土体水平有效应力差分析
桩周形成非对称冲刷坑时,桩基下游冲刷剩余土体量大于桩基上游,会造成桩基上、下游土体的水平有效应力存在差异,具体表现为桩基下游土体水平有效应力大于桩基上游。该部分就桩基上、下游的土体水平有效应力差进行参数敏感性分析。由于三维非对称局部冲刷坑模型中冲刷坑的冲刷宽度b不会引起桩基上下游的水平有效应力差,因此,此部分参数分析包括8个参数:Swt1、Swb1、Sd1、Sd2、Swt2、Swb2、d、St1。
图17~图24为8个参数影响下的冲刷坑内桩周土体水平有效应力差变化规律曲线。参与计算的土体有效重度γ′=18 kN/m3、泊松比υ=0.3。图17为桩基上游冲刷坑顶部长度Swt1逐渐增大时,桩周土体水平有效应力差变化关系曲线。由图17可以看出,Swt2=3 m时,同一深度下Swt1的增大使土体水平有效应力差逐渐增大,这种差异性随着深度的增加,出现先增大后减小的趋势,在深度4 m范围内差异性达到最大值1.8 kPa。且水平有效应力差只存在于冲刷坑底以下的一定深度范围内,即存在影响深度,影响深度以下水平有效应力差接近于0。图18为桩基上游底部冲刷长度Swb1的增大时土体水平有效应力差变化规律曲线。Swb1增大对应于桩基上游坡度β1的增大,由图18可以看出,Swb1增大时,同一深度下水平有效应力差也随之增大,Swb1的变化对水平有效应力差的影响较小,均在1 kPa以内,影响深度为8 m。图19为桩基下游顶部冲刷坑长度Swt2影响下土体水平有效应力差变化关系曲线图。Swt2的增大对应于桩基下游坡度β2的减小,由图19可以看出,Swt2增大时同一深度处水平有效应力差增大,影响深度为16 m。由图20可知,同一深度土体水平有效应力差随着Swb2的增加而减小,这是由于Swb2的不断增大,其值逐渐趋近于Swb1,使桩基上、下游侧的非对称性减小,但Swb2的变化对水平有效应力差的影响较小,均在1 kPa范围内。图21为土体水平有效应力差受桩基上游冲刷深度变化关系曲线图。可以看出,Sd1增大时土体水平有效应力差值也随之增大,最大可达到13 kPa,在深度6 m范围内差值变化明显,9 m以下深度水平有效应力差值趋近于0。图22为桩基下游冲刷深度Sd2增加时,土体水平有效应力差变化规律曲线图,由图22可知,Sd2增大时,水平有效应力差逐渐减小,这是由于Sd2增大时其值逐渐趋近于Sd1,减小了冲刷坑的非对称性。Sd2的变化对水平有效应力差的影响较大,最大值可达到12.9 kPa,影响深度为10 m。图23为St1增大时水平有效应力差变化规律曲线图。St1的增加对应于冲刷坑两侧坡度β3的增大,可知水平有效应力差随着St1的增大呈现出增大的趋势,其影响深度为10 m。图24为一非对称冲刷坑内不同桩径变化时的水平有效应力差规律曲线图。可以看出,桩径越小时,土体水平有效应力差值越大,随着桩径的增大,最大水平有效应力差值逐渐减小,最大值出现深度却在增大,其影响深度出现增大的趋势。

图17 不同Swt1下水平有效应力差随深度的变化

图18 不同Swb1下水平有效应力差随深度的变化

图19 不同Swt2下水平有效应力差随深度的变化

图20 不同Swb2下水平有效应力差随深度的变化
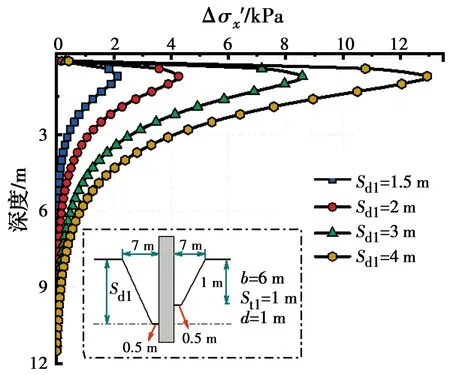
图21 不同Sd1下水平有效应力差随深度的变化

图22 不同Sd2下水平有效应力差随深度的变化

图23 不同St1下水平有效应力差随深度的变化
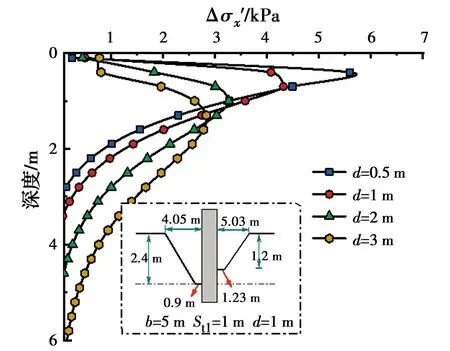
图24 不同d下水平有效应力差随深度的变化
需要注意的是,参数敏感性分析中只是对单一因素进行敏感性分析(即其他参数保持不变),而实际工程中,桩周土体的垂直有效应力及水平有效应力差值为各因素的耦合作用结果。
5 结论
基于试验实测非对称冲刷坑形态,提出了桩周非对称冲刷坑三维简化模型,且基于Boussinesq点荷载方程得到非对称冲刷坑内桩周土体应力计算方程。基于该计算方法对桩周土体的垂直有效应力及桩基上、下游水平有效应力差进行了计算,并对简化模型中的参数做了土体应力的敏感性分析,得出以下主要结论:
1)提出的冲刷坑内土体应力计算方法是将局部冲刷坑内最大冲刷深度以上土体(冲刷深度范围内冲刷剩余土体)重度作为外荷载,并基于Boussinesq点荷载方程在半无限空间中的应用得到的。而后采用有限元中“生死单元法”模拟半无限空间内冲刷坑,通过与有限元计算结果的对比,验证了计算方法的正确性。随后在半无限空间中考虑了桩径的影响,采用有限元模拟了桩周非对称冲刷坑,通过有限元计算结果与本文提出的冲刷坑内有桩存在时的理论计算结果进行对比分析,验证了考虑桩径时理论计算方法的可行性。
2)冲刷坑的形成对坑底以下一定深度土体的垂直有效应力存在较大影响,该深度称之为冲刷坑造成的影响深度,这与API、FHWA-DP中所述一致。提出的计算方法可得到任意形态冲刷坑的影响深度以及桩周土体的垂直有效应力值,弥补了API与FHWA-DP中只可以计算特定形态冲刷坑的不足,且提出的计算模型可以考虑库区等环境下冲刷坑的非对称性的影响,使得理论计算更贴合实际工程。
3)参数分析表明,桩周形成冲刷坑的尺寸越大,对冲刷坑底以下土体的垂直有效应力影响越大,影响深度也随之增大;参数敏感性分析可以得到,冲刷深度以及冲刷坑宽度的变化对桩周土体的垂直有效应力的影响最大;在影响深度以下,冲刷坑形态参数的改变对土体垂直有效应力没有影响,且影响深度以下土体的垂直有效应力值等于未形成冲刷坑时该处的垂直有效应力。
4)非对称冲刷坑会造成桩基上、下游侧土体水平有效应力存在差异,具体表现为桩基下游土体水平有效应力大于桩基上游。通过参数分析得到桩基上、下游冲刷深度的差异对桩周土体的水平有效应力差值影响最大,有效重度越大的土体,水平有效应力差值越明显。桩周土体的水平有效应力差也存在影响深度且在冲刷坑底部以下浅层土体差值最大。
