高能级强夯处理抛填路基的有效加固深度

赵家琛，吕江，赵晖，孙宏磊,3

(1.浙江大学 建筑工程学院，杭州 310058；2.杭州交通投资建设管理集团有限公司，杭州 310024；3.浙江工业大学 土木工程学院，杭州 310023)

随着交通运输工程建设持续发展，沿河流、山谷修建的公路日益增加，水下路基填筑及其强夯加固也成为必然研究的课题，对于此类工程，一般采用就地取材、开山填谷的方式回填并进行高能级强夯处理[1-2]。强夯法是一种效果显著、经济易行的地基处理及路基加固方法，自1969年Menard等[3]首创强夯法以来，发展迅速，现已推广应用到从粘性土到块石的各类地基中[4-6]。强夯有效加固深度是体现加固效果的重要指标，也是选定强夯处理方案的重要依据。对于夯击能大于6 000 kN·m的高能级强夯，相关规范[7]指出，有效加固深度需通过现场试夯或当地经验确定，同时给出了梅纳公式修正系数的参考范围，但在应用中还存在参数选取困难、结果与实际偏差较大等问题。

目前，针对高能级强夯有效加固深度的研究大多为模型试验或现场试验。Chen等[8]采用模型试验模拟现场8 000 kN·m强夯，并进行相应数值模拟，通过压实度估算有效加固深度。Feng等[9-10]通过现场试验分析了8 000、12 000 kN·m强夯处理细砂和碎石回填地基的加固效果。闫楠等[11]经现场试验分析陆域与海域回填土高能级强夯的有效加固深度，发现梅纳修正系数低于经验值。虽然已有许多学者根据工程实践总结出了一系列梅纳修正系数，但这些系数往往具有很强的经验性，对不同工程仍难以估计准确。

笔者以千黄高速千岛湖路段的抛填路基强夯处理工程为背景，采用FLAC 3D有限差分软件进行单点多次夯击的强夯数值模拟，以夯后应力作为判别标准，计算有效加固深度，并结合现场试验结果进行验证，通过参数分析，建立相应的有效加固深度经验公式，以期为类似工程提供估算依据。

1 模型介绍

1.1 计算模型

建立30 m×30 m×20 m的三维计算模型，采用六面块体网格单元，夯点位于地表中心区域。数值计算结果精确与否与单元尺寸密切相关，尤其在较为复杂的动力分析中需要考虑动荷载的频率特征。Lysmer等[12]曾提出，动力计算中网格单元尺寸Δl应满足式(1)才能准确描述波在模型中的传播。

(1)

式中：λ为最高频率对应的波长，强夯引起的振动频率一般为6～20 Hz[13]，取最高频率f为20 Hz，再使用土体参数计算p波波速Cp与波长。

(2)

(3)

在地应力平衡的静力计算阶段，采用弹性本构模型，约束模型4个侧面的横向位移和底部各方向位移，顶部为自由边界。在模拟强夯的动力计算阶段，采用基于Mohr-Coulomb破坏准则的理想弹塑性模型，在模型底部施加黏性边界，吸收边界上的入射波，形成无反射的人工边界；同时，在模型四周施加自由场边界，形成应力波的透射边界，以实现采用有限尺寸的数值模型来模拟无限尺寸的地基。流体边界部分，将模型顶部设为透水边界，其余各边界均默认不透水。土体单元网格尺寸为0.5 m，模型示意图如图1所示。

图1 数值计算模型

在模拟计算中，动力时间步的选取需保证动力计算的精度与稳定性，采用式(4)计算临界动力时间步Δtcrit[14]。

(4)

式中：V为网格六面体子单元体积；Amax为与六面体子单元相关的最大表面积。

动力问题中的阻尼设置也不可忽视，为了在数值模拟中重现自然系统在动荷载作用下的阻尼大小，采用最常用的瑞利阻尼，其中最小临界阻尼比取经验参数5%，最小中心频率采用系统的自振频率，通过模型的无阻尼自振计算获得[14]。

1.2 加载形式

强夯加载时，假定锤底应力分布均匀，不考虑夯锤与地面的接触问题，采用简化形式输入冲击荷载。强夯冲击过程只存在一个明显的应力波，参考文献[15-16]将冲击荷载简化为三角形荷载，将底面为圆形的夯锤以面积等效法化为方形进行加载。强夯荷载可分为加载阶段与卸载阶段，并考虑夯锤自重应力P1，如图2所示，冲击荷载图形与文献[17]接触力曲线基本一致，图中参数计算方法为

图2 冲击荷载示意图

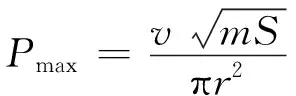
(5)

(6)

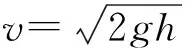
动力计算时间t3的确定还应考虑强夯所产生的应力波传播至计算边界的时间以及强夯卸荷后土体的回弹和应力释放过程。为了更好地模拟强夯加固的全过程，通过试算，最终确定每夯一次的动力计算时间为0.4 s。

1.3 土体模量的变化

随着夯击次数的增加，强夯加固范围内的土体模量会随之增加。计算模型中考虑到夯后土体工程力学性质的改善，在每次夯击后提高强夯加固范围内的土体模量。加固范围根据试算所得塑性区确定。

土体模量的增长模式采用文献[18]经过室内试验所得的经验公式

E1=E0N0.516

(7)

式中：E0为原始弹性模量、体积模量和剪切模量；N为夯击次数；E1为夯击后的模量。

2 模型验证

2.1 工程概况与土体参数

为了验证模拟结果的可靠性，选取千黄高速千岛湖路段的高能级强夯处理工程进行对比分析。千黄高速淳安段项目位于浙西北地区，整条线路所经地区地势起伏不定，相对高差较大。线路中包含16处库区路段，均需进行水下填筑路基。根据历年水文资料统计分析及现场水文调查，千岛湖水库常年水位高程稳定在97～103 m之间，本工程库区路基采用抛填块石至105 m高程后进行高能级强夯处理，夯沉至高程约103 m处设置一级平台，用于抛填的填料为项目沿线夹粉质黏土的中风化灰岩及粉砂岩等，回填厚度10～15 m。

现场抛填至设计标高后，采用设计方案确定的10 000 kN·m夯击能进行现场单点试夯，其中锤重50 t，落距20 m，锤径2.5 m。每次夯击结束后，记录累计夯沉量及单击夯沉量，现场夯击10次后满足夯沉量要求。现场夯前、夯后均进行重型动力触探试验，其中，夯后试验为点夯结束并进行场地整平后测试。数值分析模型中设置地下水位位于地表以下4 m处，材料参数依据工程勘察报告选取，如表1所示。

表1 数值分析材料参数

2.2 结果对比

将数值计算结果与现场试验区结果进行对比。由图3可见，累计夯沉量随夯击次数的增加而增大，增长趋势逐渐变缓。计算值与实测值总体较吻合，在前8击时，计算结果较实测结果偏小10%左右，最后一击实测结果与计算结果基本相同。图4中第1击时土体较为松散，单击夯沉量最大，夯后土体性质大大改善，从第2击起单击夯沉量显著减小。计算结果表明，随着夯击次数的增大，单击夯沉量不断减小。实测结果存在一定波动，推测可能原因是现场夯击至一定深度后，夯坑发生部分塌孔所致。实测总体趋势与计算结果一致，可以认为数值计算结果较合理。

图4 单击夯沉量与夯击次数的关系

图5为现场试夯区夯前与夯后的重型动力触探试验结果，由此可知，经过强夯后，地基土浅部密实度有较大提高，在5 m深度以下锤击数增大幅度明显变小，密实度提高较少，9.25 m深度以下锤击数基本没有增加，据此判断试夯区经10 000 kN·m夯击能多次点夯后，有效加固深度可达9.25 m。

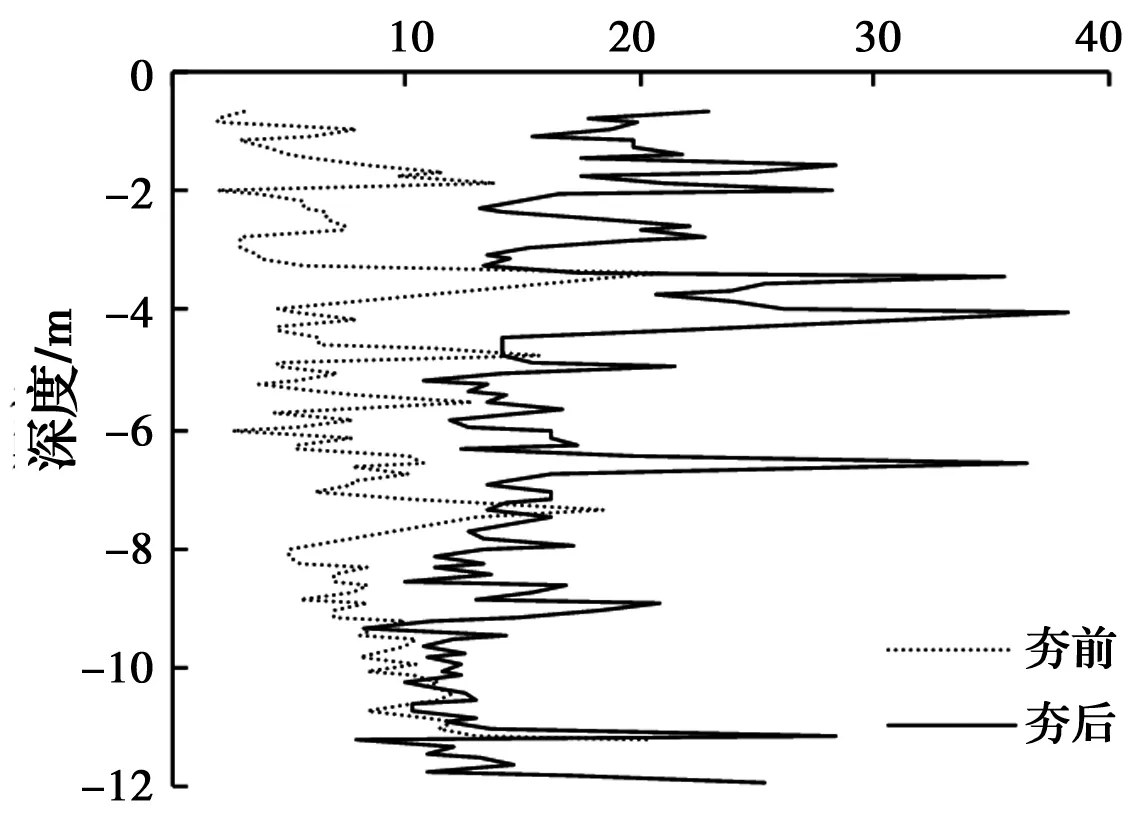
图5 重型动力触探试验结果

对于数值模拟中有效加固深度的判定，以强夯引起的附加应力需在要求深度处达到一定程度为标准，取附加应力为自重应力0.2倍的深度作为强夯有效加固深度[16,19]。在强夯模拟过程中监测竖向应力，每隔0.5 m深度设置监测点，计算各击后附加应力与初始应力之比，再根据线性差值确定有效加固深度。图6为有效加固深度随夯击次数的变化情况，在前6次夯击后有效加固深度有较为明显的增加，自第7次夯击起，有效加固深度随夯击次数的增幅非常小，最后4击仅增大2.02%。由此可见，随着夯击次数的增加，有效加固深度先增大后稳定，此后增加夯击次数不会再使有效加固深度有较大提高。模拟所得10击后的有效加固深度为9.09 m，与现场试验结果对应较好。

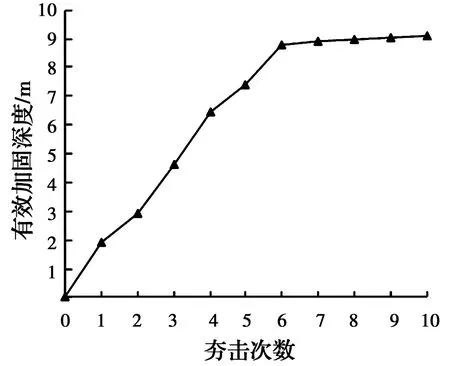
图6 有效加固深度与夯击次数的关系

3 影响因素分析

强夯有效加固深度的影响因素较多，可分为内因与外因两类：土体参数，包括弹性模量、泊松比、黏聚力、内摩擦角和密度等；施工参数，包括夯锤质量、锤径和落距等。以下分别进行分析。根据所得结果，在模拟过程中重点监测7.5～10.5 m处的竖向应力，计算10击后的有效加固深度。

3.1 土体参数分析

强夯加固过程为夯锤冲击产生的动应力在土层中不断被吸收的过程，因此，研究土体参数对强夯有效加固深度的影响。采用正交设计和极差分析方法进行分析，考虑到抛石回填土的黏聚力一般较小，变化范围不大，确定分析的基本因素为弹性模量、泊松比、内摩擦角和密度，依据现有资料[20-21]确定各参数的变动水平，见表2，在试验中黏聚力均取为5 kPa。

表2 各参数变动水平

对于正交表Ln(tm)，t为因素水平数，n为试验次数，m为因素个数。设第i个水平下第j个因素的试验结果为yij，i=1，2，…，t，j=1，2，…，m。对其进行极差分析所需的统计量记作

(8)

Rj=max(K1j,K2j,…,Kij)-min(K1j,K2j,…,Kij)

(9)

式中：Kij为第i个水平下第j个因素的统计参数；r为第i个水平下第j个因素的试验次数；yijk为第i个水平下第j个因素的第k个试验结果；Rj为极差，极差越大则该因素对试验结果的敏感性越高。

由此设计四因素三水平正交表L9(34)，施工参数与工程情况相同，计算各组的有效加固深度，根据式(8)、式(9)进行极差分析，结果见表3。土体参数的敏感性排序为：泊松比>密度>内摩擦角>弹性模量。由各组试验结果可知，泊松比和密度均与强夯有效加固深度存在负相关关系。

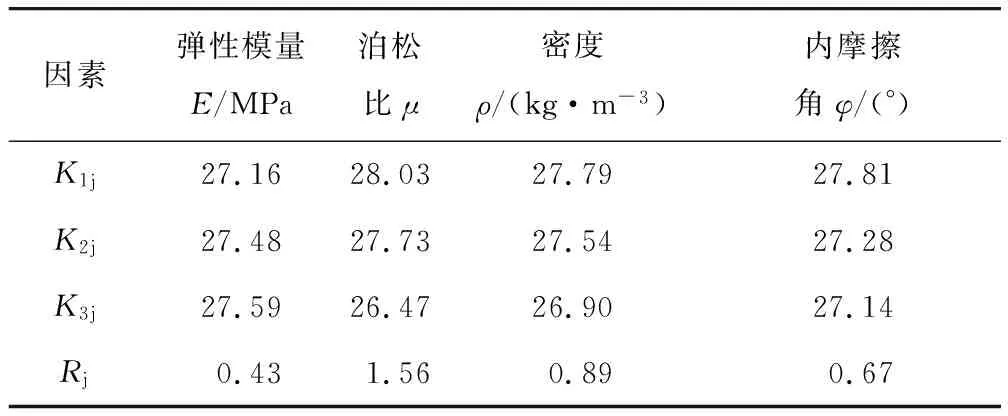
表3 极差分析结果

3.2 施工参数分析

在其他参数一定的情况下，进行单因素研究，分别讨论落距、锤重和锤径对有效加固深度的影响，土体参数见表1。

分别模拟4种不同落距的强夯工况，锤重50 t，锤径2.5 m，夯击能分别为6 000、8 000、10 000、12 000 kN·m，夯击10次。计算结果见图7，随着落距增加，强夯夯击能及最大动应力相应增大，累计夯沉量和有效加固深度均随之增大，有效加固深度的增幅相对较小。

分别模拟4种不同锤重的强夯工况，锤径2.5 m，落距20 m，夯击能分别为6 000、8 000、10 000、12 000 kN·m，夯击10次。计算结果见图8，随锤重增加，累计夯沉量和有效加固深度的变化规律与落距变化时一致。与图7情况相比，在夯击能变化范围相同时，锤重对有效加固深度的影响大于落距，原因是锤重变化不仅改变了夯击能和最大动应力，还改变了图2中t2至t3时间内的应力。将图7和图8进行联合对比可发现，在夯击能相同时，与轻锤重落的情况相比，重锤低落所得到的夯沉量与有效加固深度均更大。

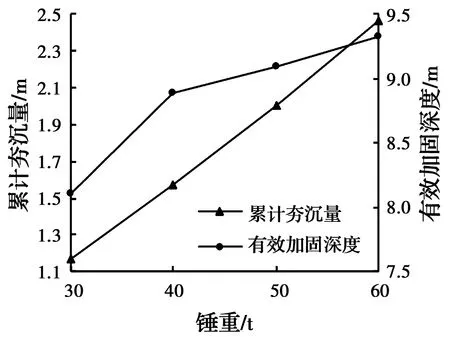
图8 锤重变化计算结果

分别模拟3种夯锤直径的工况，锤重50 t，落距20 m，夯击10次，夯击能为10 000 kN·m。计算结果如图9所示，随着夯锤直径增加，最大动应力减小，累计夯沉量及有效加固深度均随之减小，有效加固深度的变化幅度同样小于累计夯沉量。

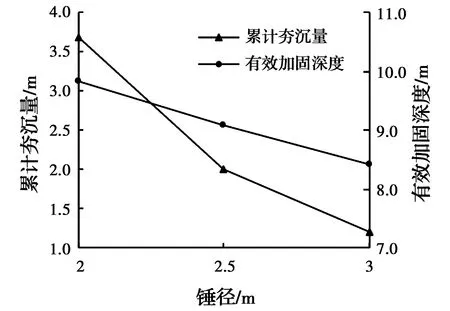
图9 锤径变化计算结果

4 公式建立

由土体参数及施工参数对有效加固深度的影响分析结果，建立有效加固深度H与土体泊松比、密度、落距、锤重和锤径的关系。考虑各参数与有效加固深度的相关关系，并结合量纲分析法，建立公式

(10)

式中：α为系数；M为夯锤质量，kg；h为落距，m；μ为泊松比；D为夯锤直径，m；ρ为土体密度，kg/m3。

对公式进行量纲分析得

(11)

将各影响因素对有效加固深度的分析结果代入式(10)，得到α的范围为1.03～1.22，采用α的均值1.10代入式(10)，计算各组强夯有效加固深度，并与数值模拟计算结果进行对比，如图10所示。将α均值代入公式计算所得的结果偏差均在10%以内，最大偏差出现在第4组的9.65%，为锤重50 t，落距12 m的情况，而相同夯击能的第8组结果偏差较小，原因是该公式无法考虑重锤低落与轻锤高落的区别，因而在第4组中低估了有效加固深度。总体上，公式计算与模拟结果基本吻合，可将该公式运用到工程实践，为同类型强夯工程提供有效加固深度的估算依据。

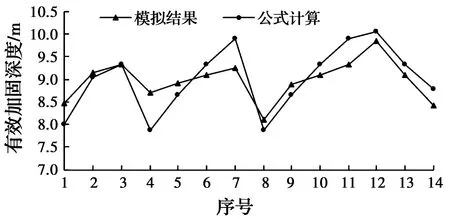
图10 有效加固深度公式计算与模拟结果对比

5 结论

利用FLAC 3D有限差分软件建立三维强夯计算模型，进行单点多次夯击的数值模拟，研究高能级强夯处理抛填路基的有效加固深度，得出以下结论：

1)随着夯击次数的增加，有效加固深度先增大后稳定，6击后增加夯击次数不会再使有效加固深度有较大提高。

2)经正交试验和极差分析得到除黏聚力外，土体参数对强夯有效加固深度的敏感性排序为泊松比>密度>内摩擦角>弹性模量，敏感性最高的泊松比与土体密度均与有效加固深度呈负相关关系。

3)落距与锤重和累计夯沉量及有效加固深度呈正相关关系，锤径则为负相关关系。锤重对有效加固深度的影响大于落距，在夯击能相同时，重锤低落所得到的夯沉量与有效加固深度均更大。