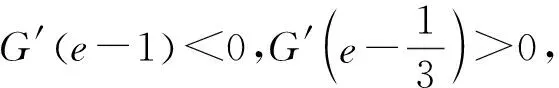素养导向下一道2021年高考题的解法探析

福建省南平市高级中学 (353000) 江智如 蔡 珺福建省南平市教师进修学院 (354200) 许贵全

1 试题呈现

(2021年高考全国I卷理科第22题)已知函数f(x)=x(1-lnx)．

(1)讨论f(x)的单调性；

2 试题分析

本试题依托函数性质，考查导数公式和导数运算法则、利用导数判断函数单调性的方法以及不等式证明相关知识，考查考生灵活运用导数工具分析问题、解决问题的能力[1]．综合考查考生化归与转化思想、推理论证能力和运算求解能力．本文在学科素养指引下，对试题进行解法探析．

3 试题解析

3.1 极值点偏移法

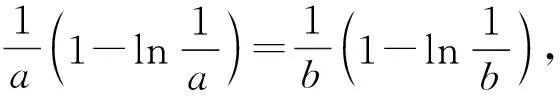
解法1：(1)由已知条件可得函数f(x)的定义域为(0,+∞)，f′(x)=-lnx，令f′(x)=-lnx=0，则x=1．当00；当x>1时，f′(x)<0．所以f(x)在(0,1)上单调递增，在(1,+∞)上单调递减.

图1

下面先证明：x1+x2>2．

要证明x1+x2>2成立，只要证明x2>2-x1成立．因为02-x1等价于f(x2)0，所以F(x)在(0,1)上单调递增，从而F(x)2成立．

再证明：x1+x2

3.2 切线放缩法

思路分析：由于解法1函数G(x)单调性的验证过程复杂，难以直接判断G(x)的正负，故考虑利用函数f(x)在(e,0)的切线判断与f(x)的大小，构造新函数运用放缩法证明结论．

解法2：由(1)可求函数f(x)在(e,0)的切线方程为：y=e-x．令H(x)=f(x)-(e-x)=2x-xlnx-e，x∈(0,e)，则H′(x)=1-lnx>0，从而H(x)在(0,e)上单调递增，于是H(x)x1，因此x1+x2

评析：导数概念及应用是高中数学教学的重要知识之一，能够让考生深刻地了解与理解不断动态变化的事物本质，提高思维层次．本试题分步设问，逐步推进，由浅入深，重点突出，从多角度考查导数的基础知识、利用导数研究函数性质的方法以及不等式的性质与应用，同时考查考生推理论证能力、运算求解能力、分析与归纳能力和化归转化思想．解法1利用极值点偏移方法求解，本质上反映函数值变化快慢的问题，是导数在函数研究中的具体应用[3]．解法2从函数切线的性质入手，运用不等式放缩法求解，从图象角度判断函数值变化的情况，揭示函数变化的几何特征．试题层次分明，区分度高，让不同水平考生思维能力的广度和深度得到展示，考查进一步数学学习的潜能，提升学生的逻辑推理素养、直观想象素养、数学建模素养、数学运算素养．

4.解法启示

函数与导数知识是高中数学教学的重难点，其中极值偏移问题是近几年高考与各地模拟考的热点，常以压轴题形式出现，突出试卷的区分性与选拔性[4]，本质是导数在函数性质研究中的应用．本文解法从学生的认知水平出发，循序渐进[4]，按照课程标准的要求，来源于教材和已学知识，又高于已有知识，提高学生导数知识的应用能力．在日常的教学实践中，教师指导学生理解与掌握导数的概念与性质，掌握极值点偏移的通法[2]，设计合理的“精致练习”[6]训练学生导数应用求解的能力，提升数学学科素养．