关于三个数学问题的推广

甘肃省兰州市红古区教育局 (730070) 王永红甘肃省兰州市第七十一中学 (730080) 庞耀辉

下面我们先证明如下引理：

引理若a1,a2,…,an≥0(n∈N且n≥4),则4(a1a2+a2a3+…+ana1)≤(a1+a2+…+an)2.

证明：设f(a1，a2，…，an)=4(a1a2+a2a3+…+ana1)-(a1+a2+…+an)2.

下面用数学归纳法证明f(a1,a2,…,an)≤0.

当n=4时,f(a1,a2,…,an)≤0等价于4(a1+a3)(a2+a4)≤(a1+a2+a3+a4)2，由均值不等式知，命题成立.

假设当n=k(k≥4,k∈N)时命题成立.则当n=k+1时，不妨设ak=min{a1,a2,…,ak,ak+1}，于是有f(a1,a2,…,ak,ak+1)-f(a1,a2,…,ak-1,ak+ak+1)=4[ak-1ak+akak+1+a1ak+1-ak-1(ak+ak+1)-(ak+ak+1)a1]=-4[(ak-1-ak)ak+1+a1ak]≤0.故f(a1,a2,…,ak,ak+1)≤f(a1,a2,…,ak-1,ak+ak+1)，由归纳假设知f(a1,a2,…,ak-1,ak+ak+1)≤0,则f(a1,a2,…,ak,ak+1)≤0.故当n=k+1时，结论也成立.

该不等式的一个推广是：

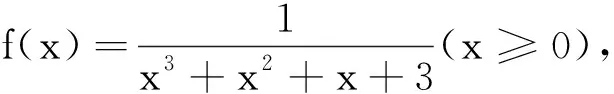
由①⟺x(x-1)2(x+1)≥0,显然成立，

故①成立，从而有

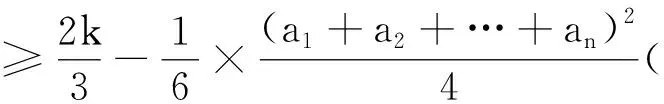
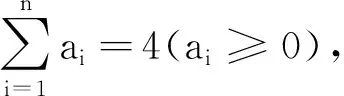
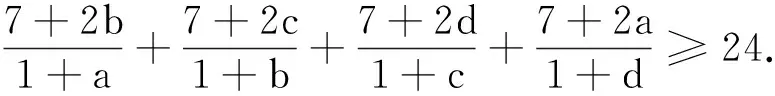
给出该不等式的一个推广是：

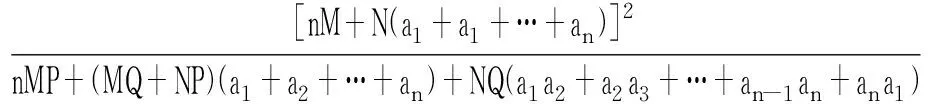
特别地，取M=7,N=2,P=Q=1，n=4，得问题2573，故命题1是问题2573的推广.

取n=4,M=N=P=Q=1，得不等式：

已知实数a,b,c,d>0,且a+b+c+d=1，求证：

该不等式的一个推广是：

由条件ab+bc+cd+da=1,并应用引理，得(a1+a2+…+an)2≥4(a1a2+a2a3+…+an-1an+ana1)=4，a1+a2+…+an≥2.

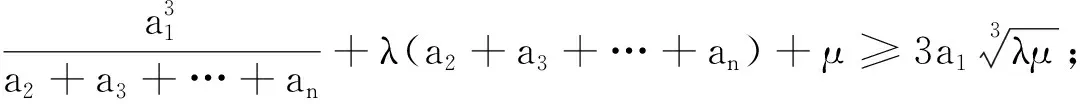
特别地，取n=4立得赛题，故命题3是赛题的一个推广.