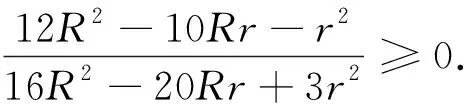Finsler-Hadwiger型不等式的推广

重庆市凤鸣山中学 (400037) 王 彬重庆市融汇沙坪坝小学 (400038) 宋雪珠

1 引言

1919年，Weitzenböck建立了如下不等式[1]：

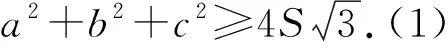
1937年，Finsler和Hadwiger给出了一个更一般的不等式[2]：

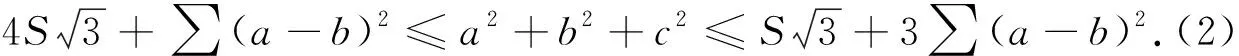
自Finsler和Hadwiger构建了(2)式之后，其推广形式层出不穷.随后，匡继昌教授在文献[3]中总结了一系列关于Finsler-Hadwiger型的不等式，其中就包括

最近，郭要红、刘其右和王洪燕三位老师分别在文献[4]和[5]中对(3)式进行了加强，得到如下定理：

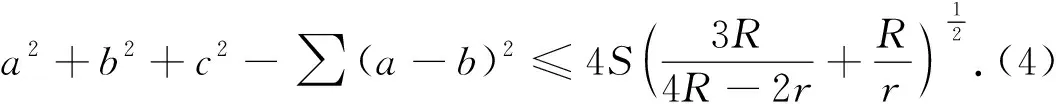
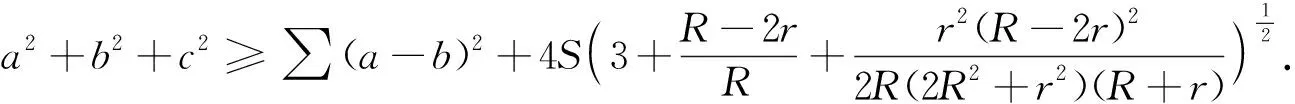
同时，李永利老师构建了如下不等式：

受到文献[4-6]的启发，笔者利用Bottema基本不等式对定理4-6中的不等式进行再加强，得到如下结论：

≤a2+b2+c2-∑(a-b)2

其中等号成立当且仅当△ABC是正三角形.

2 结论的证明

为了证明定理7，先给出一个引理：

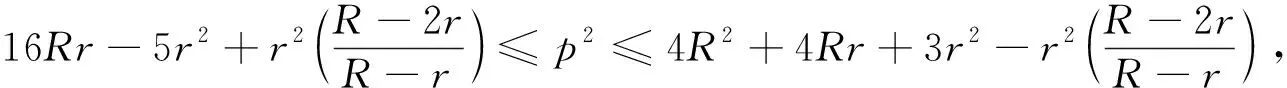
值得注意的是4R4-2R2r2-Rr3=2R2(2R+r)(R-r)+Rr(2R2-r2),再加上Euler不等式R≥2r可得

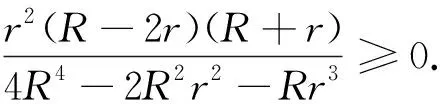
下面先证明(7)式右边的不等式.利用引理1中变形所得到的不等式可得