借得直观巧分析 执果索因妙求解——对两道导数压轴题的分析与求解

福建省福清第三中学 (350315) 何 灯福建省福清市教师进修学校 (350300) 林新建

导数试题历来给人以“繁”、“难”等印象.对于一道“繁”、“难”问题的求解，笔者认为起关键作用的是对解题方向的整理把握.如果能够透过题设条件，预测出某种结果，那么问题求解就有了方向，就可以整体把握试题，做到心中有数，就有可能执简御繁，化难为易，实现问题的轻松求解.那么，如何明确问题的求解方向？如何预期问题的最终结果？笔者认为，可借助直观实现.

本文以福建省近期举行两次检测的导数压轴题为例，谈谈如何通过直观理解，发现解题线索；直观判断，明确解题方向；直观预测，预期最终结果；严格论证，实现问题求解.

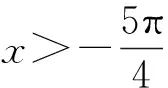
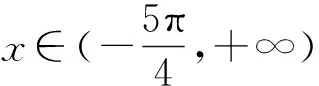
解析：(1)略；(2)g(x)≥2+ax等价ex+sinx+cosx-ax-2≥0，令F(x)=ex+sinx+cosx-ax-2，F(0)=0，F′(x)=ex+cosx-sinx-a，F′(0)=2-a，F″(x)=ex-sinx-cosx.

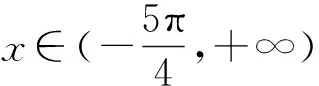
试题2 (2021届福建省高三诊断性练习第21题)已知函数f(x)=(x+3)e-x+2x.

(1)证明：f(x)恰有两个极值点；

(2)若f(x)≤ax2+3，求a的取值范围.

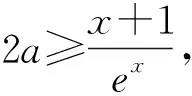
在数学学习中，借助“直观”可将不容易掌握的数学问题简单化和形象化；借助“直观”可将错综复杂的数据问题直观化与简明化；借助“直观”开展思维活动，可以成为创新型思维活动的开端.在问题解决中，教师应努力寻求直观的手段和方法，培养学生直观问题的意识和能力，努力实现“让问题在我们面前直观起来”！[1]