数学解题关键环节教学设计研究——以二道高考模拟题教学为例

淮北师范大学数学科学学院 (235000) 张 琳 张 昆

众所周知，数学解题最终表达结果为环环紧扣的逻辑过程，在诸多操作程序中存在决定问题本质的关键性的一环或几环，它或是某一程序，某种行动次序，某个正确衔接的操作方案，或者是某种程序.在组成问题解答答案的环节中，对于学生探究具体问题解决思路的某些疑难环节，称之为数学解题的“关键环节”.数学教师在解题教学设计及其课堂实施时，无需对于解题思路的每一个环节都平均使力，重在研究某些关键环节的教学活动，变向学生提供答案为启发或鼓励学生发生认识的心理过程.

一、教师应依据数学解题过程选择与确定“关键环节”

由上述的数学解题表达过程的“关键环节”概念内涵，能够认识到，数学教师在选择某道数学题进入课堂教学时，首先一定要通过自己独立探究解题思路，比对学生发生认识的心理活动过程及其个性差异，然后确定问题具体关键环节与普通环节.如此，在进行教学准备工作时，就会突出关键环节，做好设计工作.具体体现于：

数学解题的关键环节是决定题目能否获得准确解答的关键所在，也往往是学生在探究数学问题解答思路时，依据经验中的数学观念不能轻易获得的某种解答思路.只有真正突破数学解题的关键环节这一瓶颈，学生才能把握解决该类题型或掌握该种解法的真正要旨，领悟数学解题的奥秘.

由此可见，数学教师不能将数学解题的过程直接“奉献”给学生，而要想办法启发学生生成数学解题的指令.这样，解题的模式才能被纳入解题主体的头脑中，形成一种特定的操作问题信息的指令，成为一种解题模式，并比较容易地迁移到类似的探究数学解题思路活动中去.

二、数学解题关键环节处理示例

不少学生在探求数学解题关键环节处理途径时，由于对解答数学问题逻辑过程的分析和认识不全面，往往难以调用已有的数学观念，使之与相关的数学解题经验建立联系，从而经过多次尝试依然无法正确求解.因此，教师在解题教学的课堂实施过程中，首先应帮助学生正确分析数学解题的关键环节，再利用启发式(形成问题串)教学指导学生探索解题思路，萌生数学解题关键环节的处理途径，突破解题关键环节的疑难点.为了说明数学教师如何在实际解题及其教学中处理好探究解题思路的关键环节，先从2021年江苏省淮安市淮阴区数学高考模拟试题5的一道压轴题说起.

例1 (2021年江苏淮安淮阴区模拟题19)已知函数f(x)=ex|x2-a|(a≥0).

(1)当a=1时，求f(x)的单调减区间；

(2)若方程f(x)=m恰好有一个正根和一个负根，求实数m的最大值.

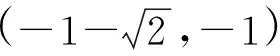
对于问题(2)，利用方程根的个数及其分布情况求参数范围，是导数综合应用中的一类典型问题.解答此类题型的首要任务是找准满足方程根的个数与分布情况的充要条件，顺藤摸瓜，逐步确定参数取值范围；其次巧用数形结合，利用已知条件及相关推导过程作出函数图象，以形助数，优化解题途径.现将解题的过程呈现如下：

图1

i)当a=0时，

f(x)=ex·x2，

f′(x)=ex·x(x+2).

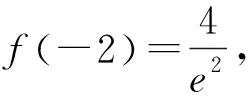
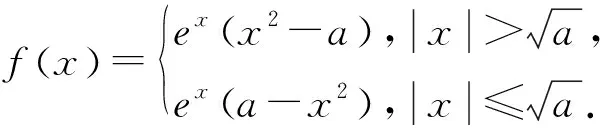
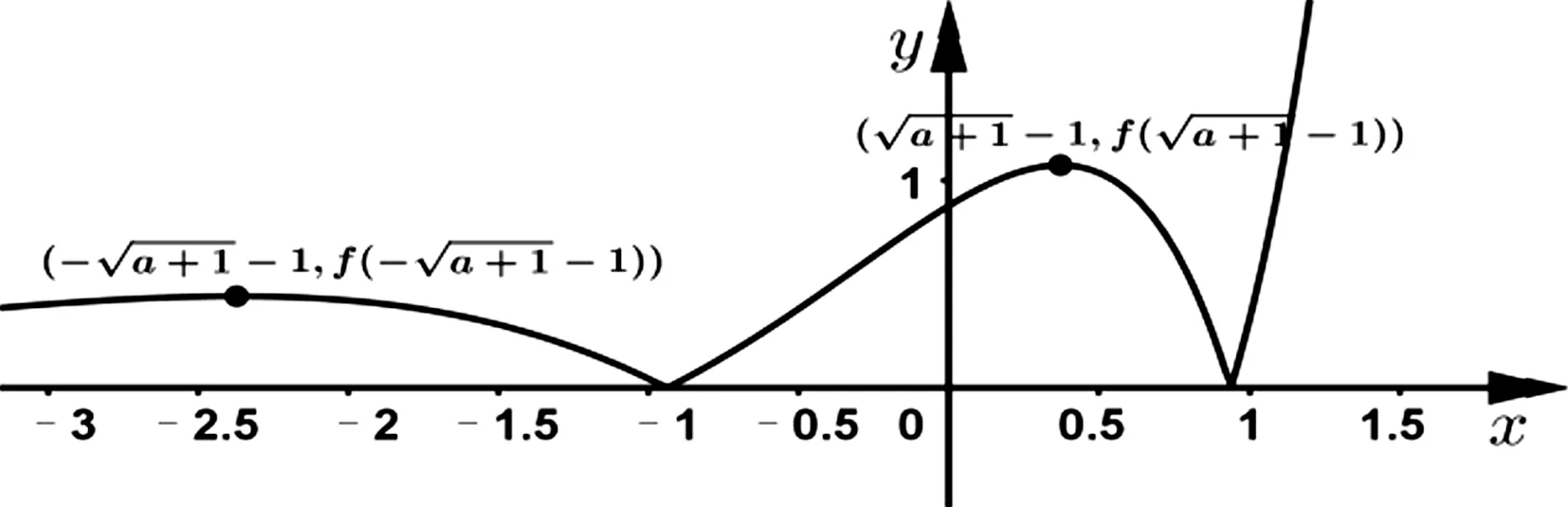
图2

图3

由上述问题(2)的解答过程，可以深刻体会到“数缺形时少直观”，“数形结合百般好”.以“数”化“形”为问题的解答提供了快捷通道，将抽象的数学问题直观化，将复杂的数学问题简单化！然而，如何“以形助数”，突破解题疑难点，获取解答思路，于许多学生而言仍力有未逮，因此构成了解答本题的关键环节.下面展示对于这一关键环节进行相应的教学设计及其课堂实施：

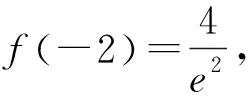
生1：由于是关于函数的问题，图象直观对发现问题的思维应该具有较好的帮助.

师：可以画出当a=0时的函数图象吗？

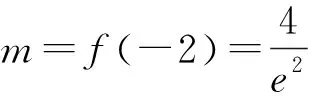
师：没错，请同学们继续讨论a>0时的情况，并尝试画出函数f(x)的大致图象.

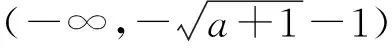
生4：据此，我画出函数f(x)的大致图象如图2所示.

生5：我画出的函数f(x)的大致图象如图3.

师：同学们认为函数f(x)的图象应该是哪一个？这两个函数图象，不同点在哪里？

师：同学们能通过计算判断两个极大值孰大孰小吗？

生：……(表示学生思维的暂时中断，下同).

师：我们发现，以计算的方式直接比较两个极值的大小存在一定困难.而图象是对函数f(x)变化趋势的直观反映，实际上也必然满足题目条件与结论的设定.因而，不妨从图象出发，从题目条件和所求结论入手，对两个函数图象进行分析判断.

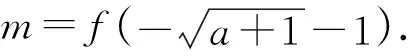
师：很好！依据同样的思路请同学们快速判断图3是否满足题意，并据此列出m应满足的条件.

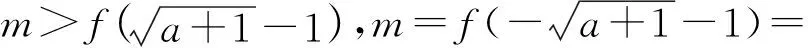
至此，题目的解答思路已相当明晰，参数m取值应满足的条件也已列出，后续的解答环节学生可以轻松应对，迎刃而解，花点时间不难得到题目答案.

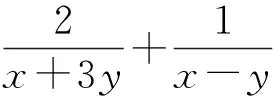
对于本题，可以使用换元法，设所求代数式中的两个分式分母分别为m,n，利用m,n反解出x,y，根据题目对x,y大小的限制条件确定m,n的范围，最后将m,n代入原式，突出结构特点，利用基本不等式求得最值.这里，巧用数值“1”转换题目的条件不等式，“化动为定”生成常数，并利用常数代换法求解.现将解题的过程呈现如下：

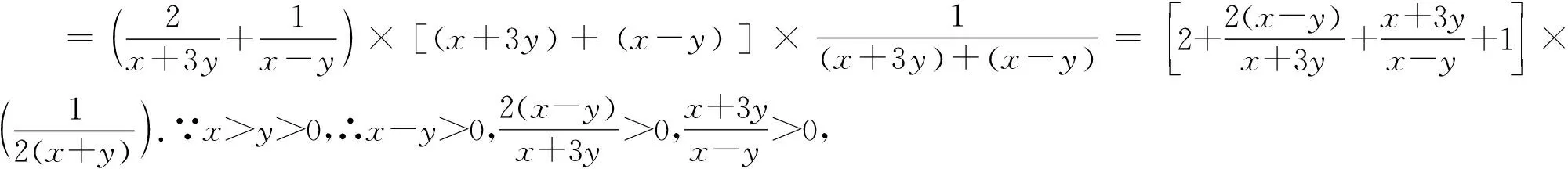
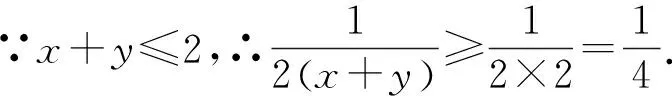
由上述的解答过程，不难发现，使用常数代换法较之于换元法对于本题的解答更加便捷高效.然而，条件x+y≤2对于本题的解答具有相当的迷惑性，如何隐蔽地启发学生萌生转换这一条件不等式为“常数1”，并利用常数代换法求解本题是解答本题的要紧之处.下面展示处理这一关键环节的教学设计：

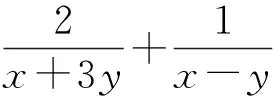
生1：我发现所求分式的分子都是常数，分母比较复杂，都含有x和y,但形式不同,也不能将两个分式直接相乘得到定值，或者相乘后得到简化并求值……

师：我们猜想，生1很可能联想到了利用基本不等式求解最值时要满足的三个关键条件“一正、二定、三相等”.他希望通过两个代数式乘积为定值的形式，得到所求代数式和的最小值，这是一个很好的解题思路.但就目前来看，从所求代数式出发，难以得到一个乘积为定值的形式.同学们能否设想一种方法，构造出一个与所求代数式乘积为定值的式子？

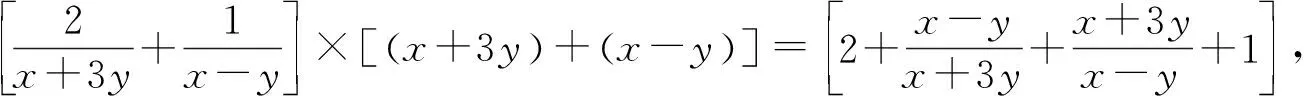
师：通过生2的方法确实能得到我们所要的乘积为定值的形式.请同学们进一步思考，这样做对我们求代数式的最小值有影响吗？能求出所求代数式的最小值吗？

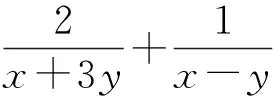
师：说得很好！那么，如何能保证引入的代数式与所求代数式相乘并且使不等号保持方向一致呢？

生4：根据不等式的基本性质，当不等式两边都乘以(或除以)同一个正数,不等号的方向不变.

师：生5的思维可真敏捷！按照这样的思路，请同学们继续后续的解题吧.

对于本题关键环节的处理，已经通过问题串的形式展现得淋漓尽致.由于后续的解题环节不构成本题解答的关键环节，这里不再赘述.至此可见，学生数学解题的过程并不是一蹴而就，一帆风顺的.如在本题的解答过程中，学生经历了对题目所求代数式形式特点的考察与条件不等式的使用探索，方能从“二定”这一解答的基本思路中突破疑点，获得正确的解答思路.

三、结语

数学解题是数学学习的必经途径.要想充分发挥数学解题的有效性，教师就必须做好数学解题关键环节课堂实施的精心设计.如在探求2021年江苏省淮安市淮阴区数学高考模拟试题5中的19题第二小问时，要得到a>0时函数f(x)的图象，就要考察两个极大值孰大孰小，而这两个数值大小的比较难以通过计算直接得到.因此在教学中，教师就要设法引导学生发现解析式与图象的对应关系，并以题目条件与结论为判别依据，确定符合题意的函数图象，再据此推导参数m取值应满足的条件.在探求14题时，转化条件不等式，“化动为定”，生成常数，并确定使用常数代换法解答题目是解题此题的关键.对于这一关键解题环节的处理，要求教师从一般化的解题思路出发，比对已知条件与所求代数式形式，引导学生发现欠缺的解题条件并萌生构造代数式及转化题目条件的解题思路，从而逐步向答案求解的方向靠近.总而言之，把握数学解题关键环节的教学设计需要教师投入足够的心力，精准发现学生数学解题的疑难困惑，做教学的有心人.唯有如此，才能最大限度地发挥数学解题对于学生数学学习的效能.